1.2: Quantidades e unidades físicas
- Page ID
- 194237
objetivos de aprendizagem
Ao final desta seção, você poderá:
- Execute conversões de unidades nas unidades SI e em inglês.
- Explique os prefixos mais comuns nas unidades SI e seja capaz de escrevê-los em notação científica.
A variedade de objetos e fenômenos estudados em física é imensa. Da vida útil incrivelmente curta de um núcleo à idade da Terra, dos pequenos tamanhos das partículas subnucleares à vasta distância até as bordas do universo conhecido, da força exercida por uma pulga saltadora à força entre a Terra e o Sol, existem fatores suficientes\(10\) para desafiar o imaginação até mesmo do cientista mais experiente. Fornecer valores numéricos para quantidades físicas e equações para princípios físicos nos permite entender a natureza muito mais profundamente do que apenas a descrição qualitativa. Para compreender essas vastas faixas, também devemos ter unidades aceitas nas quais expressá-las. E descobriremos que (mesmo na discussão potencialmente mundana de metros, quilogramas e segundos) surge uma profunda simplicidade da natureza — todas as quantidades físicas podem ser expressas como combinações de apenas quatro quantidades físicas fundamentais: comprimento, massa, tempo e corrente elétrica.

Definimos uma quantidade física especificando como ela é medida ou declarando como ela é calculada a partir de outras medições. Por exemplo, definimos distância e tempo especificando métodos para medi-los, enquanto definimos a velocidade média afirmando que ela é calculada como a distância percorrida dividida pelo tempo de viagem.
As medições de quantidades físicas são expressas em termos de unidades, que são valores padronizados. Por exemplo, a duração de uma corrida, que é uma quantidade física, pode ser expressa em unidades de metros (para velocistas) ou quilômetros (para corredores de longa distância). Sem unidades padronizadas, seria extremamente difícil para os cientistas expressar e comparar os valores medidos de forma significativa (Figura\(\PageIndex{2}\)).
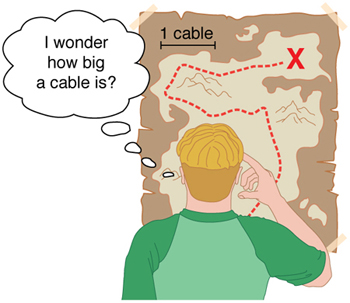
Existem dois sistemas principais de unidades usados no mundo: unidades SI (também conhecidas como sistema métrico) e unidades inglesas (também conhecidas como sistema consuetudinário ou imperial). As unidades inglesas foram historicamente usadas em nações que já foram governadas pelo Império Britânico e ainda são amplamente usadas nos Estados Unidos. Praticamente todos os outros países do mundo agora usam unidades SI como padrão; o sistema métrico também é o sistema padrão acordado por cientistas e matemáticos. A sigla “SI” é derivada do francês Système International.
Unidades SI: Unidades fundamentais e derivadas
A tabela\(\PageIndex{1}\) fornece as unidades fundamentais do SI que são usadas em todo este livro didático. Este texto usa unidades não SI em algumas aplicações em que elas são de uso muito comum, como a medição da pressão arterial em milímetros de mercúrio (mm Hg). Sempre que unidades não SI forem discutidas, elas serão vinculadas às unidades SI por meio de conversões.
| Comprimento | Missa | Hora | Corrente elétrica |
|---|---|---|---|
| metro (m) | quilograma (kg) | segundo (s) | amperes (A) |
É um fato intrigante que algumas quantidades físicas são mais fundamentais do que outras e que as quantidades físicas mais fundamentais só podem ser definidas em termos do procedimento usado para medi-las. As unidades nas quais são medidas são, portanto, chamadas de unidades fundamentais. Neste livro didático, as quantidades físicas fundamentais são consideradas comprimento, massa, tempo e corrente elétrica. (Observe que a corrente elétrica não será introduzida até muito mais tarde neste texto.) Todas as outras grandezas físicas, como força e carga elétrica, podem ser expressas como combinações algébricas de comprimento, massa, tempo e corrente (por exemplo, velocidade é comprimento dividido pelo tempo); essas unidades são chamadas de unidades derivadas.
Unidades de tempo, comprimento e massa: o segundo, o metro e o quilograma
O segundo
A unidade SI para o tempo, a segunda (abreviada como s), tem uma longa história. Por muitos anos, foi definido como 1/86.400 de um dia solar médio. Mais recentemente, um novo padrão foi adotado para obter maior precisão e definir o segundo em termos de um fenômeno físico não variável ou constante (porque o dia solar está ficando mais longo devido à desaceleração muito gradual da rotação da Terra). É possível fazer com que os átomos de césio vibrem de forma muito constante, e essas vibrações podem ser facilmente observadas e contadas. Em 1967, a segunda foi redefinida como o tempo necessário para 9.192.631.770 dessas vibrações (Figura\(\PageIndex{3}\)). A precisão nas unidades fundamentais é essencial, porque todas as medições são expressas em termos de unidades fundamentais e não podem ser mais precisas do que as próprias unidades fundamentais.

O medidor
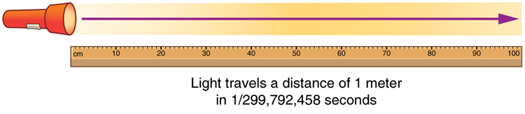
A unidade SI para comprimento é o medidor (abreviado m); sua definição também mudou com o tempo para se tornar mais precisa e precisa. O medidor foi definido pela primeira vez em 1791 como 1/10.000.000 da distância do equador ao Pólo Norte. Essa medição foi aprimorada em 1889 ao redefinir o medidor para ser a distância entre duas linhas gravadas em uma barra de platina-irídio agora mantida perto de Paris. Em 1960, tornou-se possível definir o medidor com ainda mais precisão em termos do comprimento de onda da luz, então ele foi novamente redefinido como 1.650.763,73 comprimentos de onda de luz laranja emitida por átomos de criptônio. Em 1983, o medidor recebeu sua definição atual (parcialmente para maior precisão) como a distância que a luz percorre no vácuo em 1/299.792.458 de segundo (Figura\(\PageIndex{4}\)). Essa mudança define a velocidade da luz em exatamente 299.792.458 metros por segundo. O comprimento do medidor mudará se a velocidade da luz algum dia for medida com maior precisão.
O quilograma
A unidade SI para massa é o quilograma (kg abreviado); é definida como a massa de um cilindro de platina-irídio mantido com o antigo padrão de medidor no Bureau Internacional de Pesos e Medidas, perto de Paris. Réplicas exatas do quilograma padrão também são mantidas no Instituto Nacional de Padrões e Tecnologia dos Estados Unidos, ou NIST, localizado em Gaithersburg, Maryland, fora de Washington D.C., e em outros locais ao redor do mundo. Em última análise, a determinação de todas as outras massas pode ser atribuída a uma comparação com a massa padrão.
A corrente elétrica e sua unidade acompanhante, o ampere, serão introduzidas na Introdução à Corrente Elétrica, Resistência e Lei de Ohm quando a eletricidade e o magnetismo estiverem cobertos. Os módulos iniciais deste livro didático tratam de mecânica, fluidos, calor e ondas. Nesses assuntos, todas as quantidades físicas pertinentes podem ser expressas em termos das unidades fundamentais de comprimento, massa e tempo.
Prefixos métricos
As unidades SI fazem parte do sistema métrico. O sistema métrico é conveniente para cálculos científicos e de engenharia porque as unidades são categorizadas por fatores de 10. A Tabela 2 fornece prefixos métricos e símbolos usados para denotar vários fatores de 10.
Os sistemas métricos têm a vantagem de que as conversões de unidades envolvem apenas potências de 10. Há 100 centímetros em um metro, 1000 metros em um quilômetro e assim por diante. Em sistemas não métricos, como o sistema de unidades usuais dos EUA, as relações não são tão simples — há 12 polegadas em um pé, 5280 pés em uma milha e assim por diante. Outra vantagem do sistema métrico é que a mesma unidade pode ser usada em faixas extremamente grandes de valores simplesmente usando um prefixo métrico apropriado. Por exemplo, as distâncias em metros são adequadas na construção, enquanto as distâncias em quilômetros são apropriadas para viagens aéreas, e a pequena medida de nanômetros é conveniente no design óptico. Com o sistema métrico, não há necessidade de inventar novas unidades para aplicações específicas.
O termo ordem de magnitude se refere à escala de um valor expresso no sistema métrico. Cada potência de 1 0 no sistema métrico representa uma ordem diferente de magnitude. Por exemplo, 10 1, 10 2, 10 3 e assim por diante são todas ordens de magnitude diferentes. Todas as quantidades que podem ser expressas como um produto de uma potência específica de 10 são consideradas da mesma ordem de magnitude. Por exemplo, o número 800 pode ser escrito como 8 × 10 2 e o número 450 pode ser escrito como 4,5 × 10 2. Assim, os números 800 e 450 são da mesma ordem de magnitude: 10 2. A ordem de magnitude pode ser considerada como uma estimativa aproximada da escala de um valor. O diâmetro de um átomo é da ordem de 10 a 9 m, enquanto o diâmetro do Sol é da ordem de 10 a 9 m.
A BUSCA POR PADRÕES MICROSCÓPICOS PARA UNIDADES BÁSICAS
As unidades fundamentais descritas neste capítulo são aquelas que produzem a maior exatidão e precisão na medição. Há uma sensação entre os físicos de que, como existe uma subestrutura microscópica subjacente à matéria, seria muito satisfatório basear nossos padrões de medição em objetos microscópicos e fenômenos físicos fundamentais, como a velocidade da luz. Um padrão microscópico foi alcançado para o padrão de tempo, que é baseado nas oscilações do átomo de césio.
O padrão de comprimento já foi baseado no comprimento de onda da luz (um comprimento em pequena escala) emitido por um certo tipo de átomo, mas foi suplantado pela medição mais precisa da velocidade da luz. Se for possível medir a massa de átomos ou um arranjo específico de átomos, como uma esfera de silício, com maior precisão do que o padrão do quilograma, pode ser possível basear as medições de massa em pequena escala. Também há possibilidades de que fenômenos elétricos em pequena escala possam algum dia nos permitir basear uma unidade de carga na carga de elétrons e prótons, mas atualmente a corrente e a carga estão relacionadas a correntes e forças em grande escala entre os fios.
| Prefixo | Símbolo | Valor | Exemplos (alguns são aproximados) | |
|---|---|---|---|---|
| exame | E | \(10^18\) | Exameter Em\(10^{18}m\) | distância que a luz viaja em um século |
| peta | P | \(10^15\) | petassegundo Ps\(10^{15} s\) | 30 milhões de anos |
| tera | T | \(10^12\) | TW de terawatt\(10^{12} W\) | saída de laser poderosa |
| giga | G | \(10^9\) | gigahertz GHz\(10^9 Hz\) | uma frequência de microondas |
| mega | M | \(10^6\) | megacurie MCi\(10^{6 }Ci\) | alta radioatividade |
| quilo | k | \(10^3\) | quilômetro km\(10^3 m\) | cerca de 6/10 milhas |
| hecto | h | \(10^2\) | hectolitro hL\(10^2 L\) | 26 galões |
| deka | dia | \(10^1\) | dia do diagrama\(10^g\) | colher de chá de manteiga |
| — | — | \(10^0 (=1)\) | ||
| deci | d | \(10^{−1}\) | decilitro dL\(10^{−1} L\) | menos da metade de um refrigerante |
| centi | c | \(10^{−2}\) | centímetro cm\(10^{−2} m\) | espessura da ponta do dedo |
| mili | m | \(10^{−3}\) | milímetro mm\(10^{−3} m\) | pulga em seus ombros |
| micro | µ | \(10^{−6}\) | micrômetro µm\(10^{−6} m\) | detalhe no microscópio |
| nano | n | \(10^{−9}\) | nanograma ng\(10^{−9} g\) | pequena partícula de poeira |
| pico | p | \(10^{−12}\) | picofarad pF\(10^{−12} F\) | pequeno capacitor no rádio |
| femto | f | \(10^{−15}\) | femtômetro cm\(10^{−15} m\) | tamanho de um próton |
| tatuagem | uma | \(10^{−18}\) | em segundo lugar\(10^{−18} s\) | luz do tempo cruza um átomo |
Intervalos conhecidos de comprimento, massa e tempo
A vastidão do universo e a amplitude sobre a qual a física se aplica são ilustradas pela ampla variedade de exemplos de comprimentos, massas e tempos conhecidos na Tabela\(\PageIndex{2}\). O exame desta tabela lhe dará uma ideia da variedade de tópicos e valores numéricos possíveis (figuras\(\PageIndex{5}\) e\(\PageIndex{6}\)).
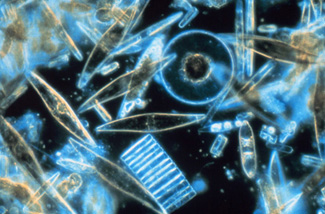

Conversão de unidades e análise dimensional
Muitas vezes, é necessário converter de um tipo de unidade para outro. Por exemplo, se você estiver lendo um livro de receitas europeu, algumas quantidades podem ser expressas em unidades de litros e você precisa convertê-las em xícaras. Ou talvez você esteja lendo as instruções de caminhada de um local para outro e esteja interessado em saber quantos quilômetros estará andando. Nesse caso, você precisará converter unidades de pés em milhas. Vamos considerar um exemplo simples de como converter unidades.
Digamos que queremos converter 80 metros (\(m\)) em quilômetros (\(km\)).
- A primeira coisa a fazer é listar as unidades que você tem e as unidades para as quais deseja converter. Nesse caso, temos unidades em metros e queremos converter em quilômetros.
- Em seguida, precisamos determinar um fator de conversão relacionando metros a quilômetros. Um fator de conversão é uma razão que expressa quantas de uma unidade são iguais a outra unidade. Por exemplo, há 12 polegadas em 1 pé, 100 centímetros em 1 metro, 60 segundos em 1 minuto e assim por diante. Nesse caso, sabemos que existem 1.000 metros em 1 quilômetro.
- Agora podemos configurar nossa conversão de unidades. Escreveremos as unidades que temos e as multiplicaremos pelo fator de conversão para que as unidades sejam canceladas, conforme mostrado:\[80\,\cancel{m} \times \dfrac{1\,km}{1000\,\cancel{m}} =0.08\, km\] Observe que a\(m\) unidade indesejada é cancelada, deixando apenas a unidade de km desejada. Você pode usar esse método para converter entre qualquer tipo de unidade.
Clique no Apêndice C para obter uma lista mais completa dos fatores de conversão.
| comprimentos em metros | Massas em quilogramas (valores mais precisos entre parênteses) | Tempos em segundos (valores mais precisos entre parênteses) | |||
|---|---|---|---|---|---|
| 10 −18 | Apresente o limite experimental para o menor detalhe observável |
10 −30
|
Massa de um elétron (9,11×10 −31 kg) |
10 −23
|
Hora da luz cruzar um próton |
|
10 −15
|
Diâmetro de um próton |
10 −27
|
Massa de um átomo de hidrogênio (1,67 × 10 −27 kg) |
10 −22
|
Vida média de um núcleo extremamente instável |
|
10 −14
|
Diâmetro de um núcleo de urânio |
10 −15
|
Massa de uma bactéria |
10 −15
|
Hora de uma oscilação da luz visível |
|
10 −10
|
Diâmetro de um átomo de hidrogênio |
10 −5
|
Massa de um mosquito |
10 −13 |
Hora de uma vibração de um átomo em um sólido |
|
10 −8
|
Espessura das membranas nas células de organismos vivos |
10 −2
|
Massa de um beija-flor |
10 −8
|
Hora de uma oscilação de uma onda de rádio FM |
|
10 −6
|
Comprimento de onda da luz visível |
1
|
Massa de um litro de água (cerca de um litro) |
10 −3
|
Duração de um impulso nervoso |
|
10 −3
|
Tamanho de um grão de areia |
10 2
|
Massa de uma pessoa |
1
|
Hora de um batimento cardíaco |
|
1
|
Altura de uma criança de 4 anos |
10 3
|
Massa de um carro |
10 5
|
Um dia (8,64 × 10 4 s) |
|
10 2
|
Comprimento de um campo de futebol |
10 8
|
Massa de um grande navio |
10 7
|
Um ano (y) (3,16×10 7 s) |
|
10 4
|
Maior profundidade do oceano |
10 12
|
Massa de um grande iceberg |
10 9
|
Cerca de metade da expectativa de vida de um ser humano |
|
10 7
|
Diâmetro da Terra |
10 15
|
Massa do núcleo de um cometa |
10 11
|
História gravada |
|
10 11
|
Distância da Terra ao Sol |
10 23
|
Massa da Lua (7,35×10 22 kg) |
10 17
|
Idade da Terra |
|
10 16
|
Distância percorrida pela luz em 1 ano (um ano-luz) |
10 25
|
Massa da Terra (5,97 × 10 24 kg) |
10 18
|
Idade do universo |
|
10 21 |
Diâmetro da Via Láctea |
10 30
|
Massa do Sol (1,99×10 30 kg) | ||
|
10 22
|
Distância da Terra até a galáxia grande mais próxima (Andrômeda) |
10 42
|
Massa da galáxia Via Láctea (limite superior atual) | ||
|
10 26
|
Distância da Terra até as bordas do universo conhecido |
10 53
|
Massa do universo conhecido (limite superior atual) | ||
Exemplo\(\PageIndex{1}\): Unit Conversions: A Short Drive Home
Suponha que você dirija 10,0 km da sua universidade até casa em 20,0 min. Calcule sua velocidade média (a) em quilômetros por hora (km/h) e (b) em metros por segundo (m/s). (Nota: A velocidade média é a distância percorrida dividida pelo tempo de viagem.)
Estratégia
Primeiro, calculamos a velocidade média usando as unidades fornecidas. Então, podemos obter a velocidade média nas unidades desejadas escolhendo o fator de conversão correto e multiplicando por ele. O fator de conversão correto é aquele que cancela a unidade indesejada e deixa a unidade desejada em seu lugar.
Solução para (a)
(1) Calcule a velocidade média. A velocidade média é a distância percorrida dividida pelo tempo de viagem. (Considere essa definição como dada por enquanto — a velocidade média e outros conceitos de movimento serão abordados em um módulo posterior.) Em forma de equação,
\[\text{average speed} =\dfrac{distance}{time}. \nonumber\]
(2) Substitua os valores fornecidos pela distância e pelo tempo.
\[ \begin{align*} \text{average speed} &=\dfrac{10.0\, km}{20.0\, min} \\[5pt] &=0.500 \dfrac{km}{ min}.\end{align*} \]
(3) Converter km/min em km/h: multiplique pelo fator de conversão que cancelará minutos e horas de saída. Esse fator de conversão é de 60 min/h. Assim,
\[\begin{align*} \text{average speed} &=0.500 \dfrac{km}{ min}×\dfrac{60\, min}{1 \,h} \\[5pt] &=30.0 \dfrac{km}{ h} \end{align*} \]
Discussão para (a)
Para verificar sua resposta, considere o seguinte:
(1) Certifique-se de ter cancelado corretamente as unidades na conversão da unidade. Se você tiver escrito o fator de conversão da unidade de cabeça para baixo, as unidades não serão canceladas corretamente na equação. Se você acidentalmente obtiver a proporção de cabeça para baixo, as unidades não serão canceladas; em vez disso, elas fornecerão as unidades erradas da seguinte forma:
\[\dfrac{km}{min}×\dfrac{1\, hr}{60\, min}=\dfrac{1}{60} \dfrac{km⋅hr}{ min^2}, \nonumber\]
que obviamente não são as unidades desejadas de km/h.
(2) Verifique se as unidades da resposta final são as unidades desejadas. O problema nos pediu que resolvêssemos a velocidade média em unidades de km/h e, de fato, obtivemos essas unidades.
(3) Verifique os números significativos. Como cada um dos valores dados no problema tem três números significativos, a resposta também deve ter três números significativos. A resposta 30,0 km/h realmente tem três números significativos, então isso é apropriado. Observe que os valores significativos no fator de conversão não são relevantes porque uma hora é definida como 60 minutos, portanto, a precisão do fator de conversão é perfeita.
(4) Em seguida, verifique se a resposta é razoável. Vamos considerar algumas informações do problema: se você viajar 10 km em um terço de uma hora (20 minutos), você viajaria três vezes mais longe em uma hora. A resposta parece razoável.
Solução para (b)
Existem várias maneiras de converter a velocidade média em metros por segundo.
(1) Comece com a resposta para (a) e converta km/h em m/s. São necessários dois fatores de conversão: um para converter horas em segundos e outro para converter quilômetros em metros.
(2) Multiplicação por esses rendimentos
\[\begin{align*} \text{Average speed} &=30.0\dfrac{\bcancel{km}}{\cancel{h}}×\dfrac{1\,\cancel{h}}{3,600 \,s}×\dfrac{1,000\,m}{1\, \bcancel{km}} \\[5pt] &=8.33 \,m/s \end{align*}\]
Discussão para (b)
Se tivéssemos começado com 0,500 km/min, precisaríamos de fatores de conversão diferentes, mas a resposta teria sido a mesma: 8,33 m/s.
Você deve ter notado que as respostas no exemplo trabalhado que acabamos de abordar foram dadas com três dígitos. Por quê? Quando você precisa se preocupar com o número de dígitos em algo que você calcula? Por que não anotar todos os dígitos que sua calculadora produz? O módulo Precisão, Precisão e Números Significativos ajudará você a responder a essas perguntas.
UNIDADES NÃO PADRONIZADAS
Embora existam vários tipos de unidades com as quais todos estamos familiarizados, existem outras que são muito mais obscuras. Por exemplo, um firkin é uma unidade de volume que já foi usada para medir a cerveja. Um firkin equivale a cerca de 34 litros. Para saber mais sobre unidades não padronizadas, use um dicionário ou enciclopédia para pesquisar diferentes “pesos e medidas”. Anote todas as unidades incomuns, como um grão de cevada, que não estão listadas no texto. Pense em como a unidade é definida e declare sua relação com as unidades SI.
Exercício\(\PageIndex{1}\)
Alguns beija-flores batem suas asas mais de 50 vezes por segundo. Um cientista está medindo o tempo necessário para um beija-flor bater suas asas uma vez. Qual unidade fundamental o cientista deve usar para descrever a medição? Qual fator de 10 o cientista provavelmente usará para descrever o movimento com precisão? Identifique o prefixo métrico que corresponde a esse fator de 10.
- Resposta
-
O cientista medirá o tempo entre cada movimento usando a unidade fundamental de segundos. Como as asas batem tão rápido, o cientista provavelmente precisará medir em milissegundos, ou 10 −3 segundos. (50 batimentos por segundo correspondem a 20 milissegundos por batida).
Exercício\(\PageIndex{2}\)
Um centímetro cúbico é igual a um mililitro. O que isso diz sobre as diferentes unidades no sistema métrico SI?
- Resposta
-
A unidade fundamental de comprimento (metro) provavelmente é usada para criar a unidade derivada de volume (litro). A medida de um mililitro depende da medida de um centímetro.
Resumo
- Quantidades físicas são uma característica ou propriedade de um objeto que pode ser medida ou calculada a partir de outras medidas.
- As unidades são padrões para expressar e comparar a medição de quantidades físicas. Todas as unidades podem ser expressas como combinações de quatro unidades fundamentais.
- As quatro unidades fundamentais que usaremos neste texto são o metro (para comprimento), o quilograma (para massa), a segunda (para tempo) e o ampere (para corrente elétrica). Essas unidades fazem parte do sistema métrico, que usa potências de 10 para relacionar quantidades nas vastas faixas encontradas na natureza.
- As quatro unidades fundamentais são abreviadas da seguinte forma: metro, m; quilograma, kg; segundo, s; e ampère, A. O sistema métrico também usa um conjunto padrão de prefixos para indicar cada ordem de magnitude maior ou menor que a própria unidade fundamental.
- As conversões de unidades envolvem a alteração de um valor expresso em um tipo de unidade para outro tipo de unidade. Isso é feito usando fatores de conversão, que são índices que relacionam quantidades iguais de unidades diferentes.
Glossário
- quantidade física
- uma característica ou propriedade de um objeto que pode ser medida ou calculada a partir de outras medidas
- unidades
- um padrão usado para expressar e comparar medidas
- Unidades SI
- o sistema internacional de unidades que cientistas da maioria dos países concordaram em usar; inclui unidades como metros, litros e gramas
- Unidades inglesas
- sistema de medição usado nos Estados Unidos; inclui unidades de medida, como pés, galões e libras
- unidades fundamentais
- unidades que só podem ser expressas em relação ao procedimento usado para medi-las
- unidades derivadas
- unidades que podem ser calculadas usando combinações algébricas das unidades fundamentais
- segundo
- a unidade SI para o tempo, abreviada (s)
- contador
- a unidade SI para comprimento, abreviada (m)
- quilograma
- a unidade SI para massa, abreviada (kg)
- sistema métrico
- um sistema no qual os valores podem ser calculados em fatores de 10
- ordem de grandeza
- refere-se ao tamanho de uma quantidade no que se refere a uma potência de 10
- fator de conversão
- uma proporção que expressa quantas de uma unidade são iguais a outra unidade


