Skip to main content
Global

11.5: Hipérboles

  1. Last updated
  2. Save as PDF
  • Page ID
    183717

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Faça um gráfico de uma hipérbole com centro em\((0,0)\)
    • Faça um gráfico de uma hipérbole com centro em\((h,k)\)
    • Identifique seções cônicas por suas equações

    Antes de começar, faça este teste de prontidão.

    1. Resolver:\(x^{2}=12\).
      Se você perdeu esse problema, consulte o Exemplo 9.1.
    2. Expandir:\((x−4)^{2}\).
      Se você perdeu esse problema, consulte o Exemplo 5.32.
    3. Gráfico\(y=-\frac{2}{3} x\).
      Se você perdeu esse problema, consulte o Exemplo 3.4.

    Faça um gráfico de uma hipérbola com o centro em\((0,0)\)

    A última seção cônica que examinaremos é chamada de hipérbole. Veremos que a equação de uma hipérbole parece a mesma de uma elipse, exceto que é uma diferença e não uma soma. Embora as equações de uma elipse e de uma hipérbole sejam muito semelhantes, seus gráficos são muito diferentes.

    Definimos uma hipérbole como todos os pontos em um plano em que a diferença de suas distâncias de dois pontos fixos é constante. Cada um dos pontos fixos é chamado de foco da hipérbole.

    Definição\(\PageIndex{1}\)

    Uma hipérbole são todos os pontos em um plano onde a diferença de suas distâncias de dois pontos fixos é constante. Cada um dos pontos fixos é chamado de foco da hipérbole.

    A figura mostra um cone circular direito de dupla soneca cortado por um plano paralelo ao eixo vertical do cone formando uma hipérbole. A figura é rotulada como “hipérbolaâ €™.
    Figura 11.4.1

    A linha que passa pelos focos é chamada de eixo transversal. Os dois pontos em que o eixo transversal cruza a hipérbole são, cada um, um vértice da hipérbole. O ponto médio do segmento que une os focos é chamado de centro da hipérbole. A linha perpendicular ao eixo transversal que passa pelo centro é chamada de eixo conjugado. Cada pedaço do gráfico é chamado de ramo da hipérbole.

    A figura mostra dois gráficos de uma hipérbole. O primeiro gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulos. O centro da hipérbole é a origem. Os vértices e focos são mostrados com pontos que estão no eixo transversal, que é o eixo x. Os galhos passam pelos vértices e se abrem para a esquerda e para a direita. O eixo y é o eixo conjugado. O segundo gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulos. O centro da hipérbole é a origem. Os vértices e focos são mostrados com pontos que estão no eixo transversal, que é o eixo y. Os galhos passam pelos vértices e se abrem para cima e para baixo. O eixo x é o eixo conjugado.
    Figura 11.4.2

    Novamente, nosso objetivo é conectar a geometria de uma cônica com a álgebra. Colocar a hipérbole em um sistema de coordenadas retangulares nos dá essa oportunidade. Na figura, colocamos a hipérbole de forma que\(((−c,0),(c,0))\) os focos fiquem no\(x\) eixo -e o centro seja a origem.

    A figura mostra o gráfico de uma hipérbole. O gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulos. O centro da hipérbole é a origem. Os focos (menos c, 0) e (c, 0) são marcados com um ponto e estão no eixo x. Os vértices são marcados com um ponto e estão no eixo x. Os galhos passam pelos vértices e se abrem para a esquerda e para a direita. A distância de (menos c, 0) até um ponto na ramificação (x, y) está marcada como d sub 1. A distância de (x, y) na ramificação até (c, 0) está marcada como d sub 2.
    Figura 11.4.3

    A definição afirma que a diferença da distância entre os focos e um ponto\((x,y)\) é constante. Então\(|d_{1}−d_{2}|\) é uma constante que chamaremos\(2a\) assim\(|d_{1}-d_{2} |=2 a\). Usaremos a fórmula da distância para nos levar a uma fórmula algébrica para uma elipse.

    \(\left|d_{1} - d_{2}\right| =2 a\)

    Use a fórmula da distância para encontrar\(d_{1}, d_{2}\)

    \(\left|\sqrt{(x-(-c))^{2}+(y-0)^{2}}-\sqrt{(x-c)^{2}+(y-0)^{2}}\right|=2 a\)

    Elimine os radicais. Para simplificar a equação da elipse, deixamos\(c^{2}-a^{2}=b^{2}\).

    \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{c^{2}-a^{2}}=1\)

    Então, a equação de uma hipérbole centrada na origem na forma padrão é:

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)

    Para representar graficamente a hipérbole, será útil conhecer as interceptações. Encontraremos os\(x\) -interceptos e\(y\) -interceptos usando a fórmula.

    \(x\)-intercepta

    Deixe\(y=0\).

    \(\begin{aligned} \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}}-\frac{0^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}} &=1 \\ x^{2} &=a^{2} \\ x &=\pm a \end{aligned}\)

    As\(x\) interceptações -são\((a,0)\)\((−a,0)\) e.

    \(y\)-intercepta

    Deixe\(x=0\).

    \(\begin{aligned} \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\ \frac{0^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\-\frac{y^{2}}{b^{2}} &=1 \\ y^{2} &=-b^{2} \\ y &=\pm \sqrt{-b^{2}} \end{aligned}\)

    Não há\(y\) interceptações.

    Os\(a, b\) valores na equação também nos ajudam a encontrar as assíntotas da hipérbole. As assíntotas são linhas retas que se cruzam às quais os ramos do gráfico se aproximam, mas nunca se cruzam à medida que os\(x, y\) valores ficam cada vez maiores.

    Para encontrar as assíntotas, esboçamos um retângulo cujos lados cruzam o eixo x nos vértices\((−a,0),(a,0)\) e cruzamos o\(y\) eixo -em\((0,−b), (0,b)\). As linhas que contêm as diagonais desse retângulo são as assíntotas da hipérbole. O retângulo e as assíntotas não fazem parte da hipérbole, mas nos ajudam a representar graficamente a hipérbole.

    A figura mostra o gráfico de uma hipérbole. O gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulos. O centro da hipérbole é a origem. Os vértices são (menos a, 0) e (a, 0) e são marcados com um ponto e estão no eixo x. Os pontos (0, b) e (0, negativo) estão no eixo y. Há um retângulo central cujos lados cruzam o eixo x nos vértices (menos a, 0) e (a, 0) e cruzam o eixo y em (0, b) e (0, menos b). As assíntotas são dadas por y é igual a b dividido por a vezes x e y é igual a menos b dividido por a vezes x e são desenhadas como as diagonais do retângulo central. Os ramos da hipérbole passam pelos vértices, se abrem para a esquerda e para a direita e se aproximam das assíntotas.
    Figura 11.4.4

    As assíntotas passam pela origem e podemos avaliar sua inclinação usando o retângulo que esboçamos. Eles têm equações\(y=\frac{b}{a} x\)\(y=-\frac{b}{a} x\) e.

    Existem duas equações para hipérboles, dependendo se o eixo transversal é vertical ou horizontal. Podemos dizer se o eixo transversal é horizontal observando a equação. Quando a equação está na forma padrão, se o\(x^{2}\) termo -for positivo, o eixo transversal é horizontal. Quando a equação está na forma padrão, se o\(y^{2}\) termo -for positivo, o eixo transversal é vertical.

    As segundas equações podem ser derivadas de forma semelhante ao que fizemos. Vamos resumir os resultados aqui.

    Definição\(\PageIndex{2}\)

    Forma padrão da equação: uma hipérbole com centro\((0,0)\)

    A forma padrão da equação de uma hipérbole com centro\((0,0)\) é

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \quad\)ou\(\quad \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)

    A figura mostra o gráfico de duas hipérboles. O primeiro gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulos. O centro da hipérbole é a origem. Os vértices são (menos a, 0) e (a, 0) e são marcados com um ponto e estão no eixo x. Os pontos (0, b) e (0, negativo) estão no eixo y. Há um retângulo central cujos lados cruzam o eixo x nos vértices (menos a, 0) e (a, 0) e cruzam o eixo y em (0, b) e (0, menos b). As assíntotas são dadas por y é igual a b dividido por a vezes x e y é igual a menos b dividido por a vezes x e são desenhadas como as diagonais do retângulo central. Os ramos da hipérbole passam pelos vértices, se abrem para a esquerda e para a direita e se aproximam das assíntotas. O segundo gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulos. O centro da hipérbole é a origem. Os vértices são (0, a) e (0, menos a) e são marcados com um ponto e estão no eixo y. Os pontos (0, b) e (0, negativo) estão no eixo y. Há um retângulo central cujos lados cruzam o eixo y nos vértices (0, a) e (0, menos a) e cruzam o eixo y em (menos b, 0) e (b, 0). Os ramos da hipérbole passam pelos vértices, se abrem para cima e para baixo e se aproximam das assíntotas.
    Figura 11.4.5

    Observe que, diferentemente da equação de uma elipse, o denominador de nem sempre\(x^{2}\) é\(a^{2}\) e o denominador de nem sempre\(y^{2}\) é\(b^{2}\).

    Observe que quando o\(x^{2}\) termo -é positivo, o eixo transversal está no\(x\) eixo -. Quando o\(y^{2}\) termo -é positivo, o eixo transversal está no\(y\) eixo -.

    Formas padrão da equação: uma hipérbole com centro\((0,0)\)

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)
    Orientação \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">Eixo transversal no\(x\) eixo.
    Abre à esquerda e à direita    		 \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">Eixo transversal no\(y\) eixo.
    Abre para cima e para baixo
    Vértices \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\)
    \(x\)-intercepta \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">nenhum
    \(y\)-intercepta \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">nenhum \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\)
    Retângulo \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">Usar\(( \pm a, 0)(0, \pm b)\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">Usar\((0, \pm a)( \pm b, 0)\)
    Assíntotas \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\(y=\frac{b}{a} x, y=-\frac{b}{a} x\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\(y=\frac{a}{b} x, y=-\frac{a}{b} x\)
    Tabela 11.4.1

    Usaremos essas propriedades para representar graficamente hipérboles.

    Exemplo\(\PageIndex{1}\) How to Graph a Hyperbola with Center \((0,0)\)

    Gráfico\(\frac{x^{2}}{25}-\frac{y^{2}}{4}=1\).

    Solução:

    Etapa 1: Escreva a equação no formato padrão. A equação está na forma padrão. \(\frac{x^{2}}{25}-\frac{y^{2}}{4}=1\)
    Etapa 2: Determine se o eixo transversal é horizontal ou vertical. Como o\(x^{2}\) termo -é positivo, o eixo transversal é horizontal. O eixo transversal é horizontal.
    Etapa 3: Encontre os vértices. Desde\(a^{2}=25\) então\(a=\pm 5\). Os vértices estão no\(x\) eixo -. \((-5,0),(5,0)\)
    Etapa 4: Desenhe o retângulo centrado na interseção de origem, um eixo em\(\pm a\) e outro em\(\pm b\).

    Desde então\(a=\pm 5\), o retângulo cruzará o\(x\) eixo -nos vértices.

    Desde então\(b=\pm 2\), o retângulo cruzará o\(y\) eixo -em\((0,-2)\)\((0,2)\) e.

    		 Captura de tela (148) .png

    Etapa 5: esboce as assíntotas — as linhas nas diagonais do retângulo.

    		 As assíntotas têm as equações\(y=\frac{5}{2} x, y=-\frac{5}{2} x\). Captura de tela (149) .png
    Etapa 6: Desenhe os dois ramos da hipérbole. Comece em cada vértice e use as assíntotas como guia. 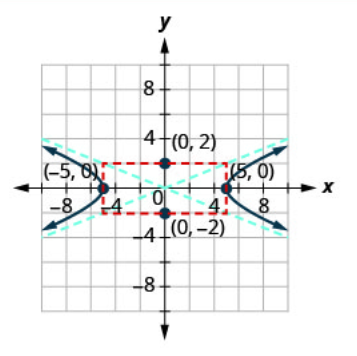Captura de tela (150) .png
    Tabela 11.4.2
    Exercício\(\PageIndex{1}\)

    Gráfico\(\frac{x^{2}}{16}-\frac{y^{2}}{4}=1\).

    Responda
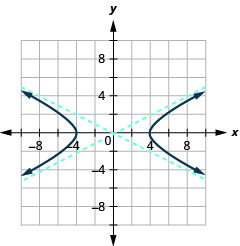
    O gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulos, com assíntotas y é igual a mais ou menos metade vezes x e ramificações que passam pelos vértices (mais ou menos 4, 0) e se abrem à esquerda e à direita.
    Figura 11.4.9
    Exercício\(\PageIndex{2}\)

    Gráfico\(\frac{x^{2}}{9}-\frac{y^{2}}{16}=1\).

    Responda
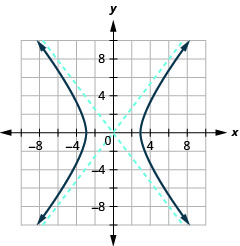
    O gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulos, com assíntotas y é igual a mais ou menos quatro terços vezes x, e ramificações que passam pelos vértices (mais ou menos 3, 0) e se abrem à esquerda e à direita.
    Figura 11.4.10

    Resumimos as etapas para referência.

    Faça um gráfico de uma hipérbole centrada em\((0,0)\)

    1. Escreva a equação na forma padrão.
    2. Determine se o eixo transversal é horizontal ou vertical.
    3. Encontre os vértices.
    4. Desenhe o retângulo centrado na origem cruzando um eixo em\(±a\) e o outro em\(±b\).
    5. Desenhe as assíntotas — as linhas nas diagonais do retângulo.
    6. Desenhe os dois ramos da hipérbole.

    Às vezes, a equação de uma hipérbole precisa ser colocada primeiro na forma padrão antes de representá-la graficamente.

    Exemplo\(\PageIndex{2}\)

    Gráfico\(4 y^{2}-16 x^{2}=64\).

    Solução:

      \(4 y^{2}-16 x^{2}=64\)
    Para escrever a equação na forma padrão, divida cada termo por\(64\) para que a equação seja igual\(1\) a. \(\frac{4 y^{2}}{64}-\frac{16 x^{2}}{64}=\frac{64}{64}\)
    Simplifique. \(\frac{y^{2}}{16}-\frac{x^{2}}{4}=1\)
    Como o\(y^{2}\) termo -é positivo, o eixo transversal é vertical. Desde\(a^{2}=16\) então\(a=\pm 4\).  
    Os vértices estão no\(y\) eixo -,\((0,-a),(0, a)\). Desde\(b^{2}=4\) então\(b=\pm 2\). \((0,-4),(0,4)\)
    Desenhe o retângulo que cruza o\(x\) eixo -em\((-2,0),(2,0)\) e o\(y\) eixo -nos vértices. Desenhe as assíntotas nas diagonais do retângulo. Desenhe os dois ramos da hipérbole. .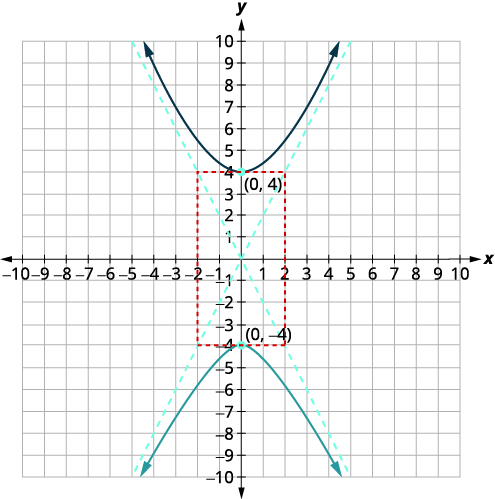
    Tabela 11.4.3
    Exercício\(\PageIndex{3}\)

    Gráfico\(4 y^{2}-25 x^{2}=100\).

    Responda
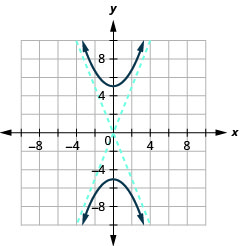
    O gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulos, com assíntotas y é igual a mais ou menos cinco metades vezes x e ramificações que passam pelos vértices (0, mais ou menos 5) e se abrem para cima e para baixo.
    Figura 11.4.12
    Exercício\(\PageIndex{4}\)

    Gráfico\(25 y^{2}-9 x^{2}=225\).

    Responda
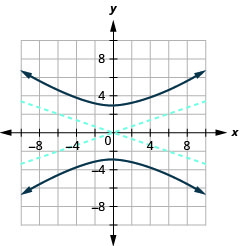
    O gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulos, com assíntotas y é igual a mais ou menos três quintos vezes x, e ramificações que passam pelos vértices (0, mais ou menos 3) e se abrem para cima e para baixo.
    Figura 11.4.13

    Faça um gráfico de uma hipérbola com o centro em\((h,k)\)

    As hipérboles nem sempre estão centradas na origem. Quando uma hipérbole está centrada nas equações,\((h,k)\) as equações mudam um pouco conforme refletido na tabela.

    Formas padrão da equação: uma hipérbole com centro\((h,k)\)

    \(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) \(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\)
    Orientação \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">O eixo transversal é horizontal. Abre à esquerda e à direita \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">O eixo transversal é vertical. Abre para cima e para baixo
    Centro \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">\((h,k)\) \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">\((h,k)\)
    Vértices \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">\(a\) unidades à esquerda e à direita do centro \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">\(a\) unidades acima e abaixo do centro
    Retângulo \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">Use\(a\) unidades à esquerda/direita das\(b\) unidades centrais acima/abaixo do centro \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">Use\(a\) unidades acima/abaixo das\(b\) unidades centrais à esquerda/direita do centro
    Tabela 11.4.4
    Exemplo\(\PageIndex{3}\) How to Graph a Hyperbola with Center \((h,k)\)

    Gráfico\(\frac{(x-1)^{2}}{9}-\frac{(y-2)^{2}}{16}=1\)

    Solução:

    Etapa 1: Escreva a equação no formato padrão. A equação está na forma padrão. \(\frac{(x-1)^{2}}{9}-\frac{(y-2)^{2}}{16}=1\)
    Etapa 2: Determine se o eixo transversal é horizontal ou vertical. Como o\(x^{2}\) termo -é positivo, a hipérbole se abre para a esquerda e para a direita. O eixo transversal é horizontal. A hipérbole se abre à esquerda e à direita.
    Etapa 3: Encontre o centro\(a, b\) e. \(h=1\)e\(k=2\)
    \(a^{2}=9\)
    \(b^{2}=16\)

    \(\begin{array} {c} \frac{\left(\stackrel{\color{red}{x-h}}{\color{black}{x-1}} \right)^{2}}{9} - \frac{\left(\stackrel{\color{red}{y-k}}{\color{black}{y-2}} \right)^{2}}{16} = 1 \end{array}\)

    Centro:\((1,2)\)

    \(a=3\)

    \(b=4\)
    Etapa 4: Desenhe o retângulo centrado no\((h,k)\) uso\(a,b\).

    Marque o centro,\((1,2)\).

    Desenhe o retângulo que passa pelas\(3\) unidades de pontos à esquerda/direita do centro e\(4\) unidades acima e abaixo do centro.

    		 Captura de tela (151) .png
    Etapa 5: esboce as assíntotas — as linhas nas diagonais do retângulo. Marque os vértices. Esboce as diagonais. Marque os vértices, que estão nas\(3\) unidades do retângulo à esquerda e à direita do centro. Captura de tela (152) .png
    Etapa 6: Desenhe os dois ramos da hipérbole. Comece em cada vértice e use as assíntotas como guia. Captura de tela (153) .png
    Tabela 11.4.5
    Exercício\(\PageIndex{5}\)

    Gráfico\(\frac{(x-3)^{2}}{25}-\frac{(y-1)^{2}}{9}=1\).

    Responda
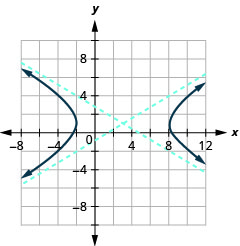
    O gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulo, com uma assíntota que passa por (menos 2, menos 2) e (8, 4) e uma assíntota que passa por (menos 2, 4) e (8, menos 2) e ramificações que passam pelos vértices ( menos 2, 2) e (8, 2) e abre para a esquerda e para a direita.
    Figura 11.4.17
    Exercício\(\PageIndex{6}\)

    Gráfico\(\frac{(x-2)^{2}}{4}-\frac{(y-2)^{2}}{9}=1\).

    Responda
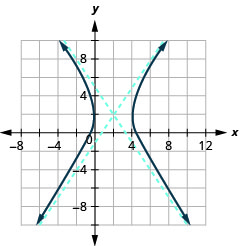
    O gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulo, com o centro (2, 2), uma assíntota que passa por (0, menos 1) e (4, 5) e uma assíntota que passa por (0, 5) e (4, menos 1) e ramificações que passam pelos vértices (0, 2) e (4, 2) e abre para a esquerda e para a direita.
    Figura 11.4.18

    Resumimos as etapas para facilitar a referência.

    Faça um gráfico de uma hipérbole centrada em\((h,k)\)

    1. Escreva a equação na forma padrão.
    2. Determine se o eixo transversal é horizontal ou vertical.
    3. Encontre o centro\(a,b\) e.
    4. Desenhe o retângulo centrado em\((h,k)\) usar\(a,b\).
    5. Desenhe as assíntotas — as linhas nas diagonais do retângulo. Marque os vértices.
    6. Desenhe os dois ramos da hipérbole.

    Tenha cuidado ao identificar o centro. A equação padrão tem\(x−h\) e\(y−k\) com o centro como\((h,k)\).

    Exemplo\(\PageIndex{4}\)

    Gráfico\(\frac{(y+2)^{2}}{9}-\frac{(x+1)^{2}}{4}=1\).

    Solução:

      .
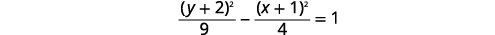    Como o\(y^{2}\) termo -é positivo, a hipérbole se abre para cima e para baixo. .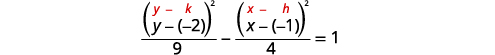
    Encontre o centro,\((h,k)\). Centro:\((-1,-2)\)
    Encontre\(a,b\). \(a=3 b=2\)
    Desenhe o retângulo que passa pelas\(3\) unidades de pontos acima e abaixo do centro e
    \(2\) unidades à esquerda/direita do centro.
    Desenhe as assíntotas — as linhas nas diagonais do retângulo.
    Marque os vértices.
    Faça um gráfico dos galhos.    		 .
    Tabela 11.4.6
    Exercício\(\PageIndex{7}\)

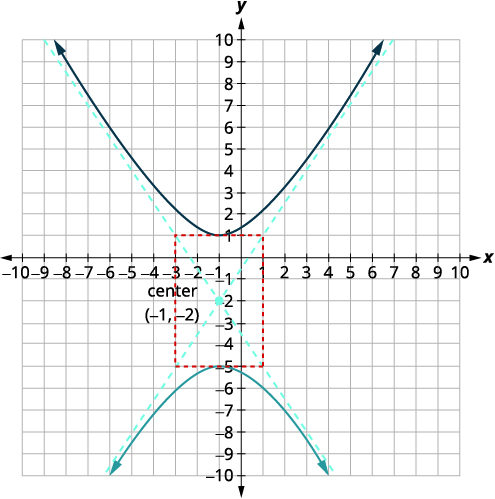    Gráfico\(\frac{(y+3)^{2}}{16}-\frac{(x+2)^{2}}{9}=1\).

    Responda
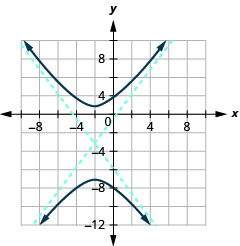
    O gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulo, com um centro em (menos 2, menos 3), uma assíntota que passa por (menos 5, menos 7) e (1, 1) e uma assíntota que passa por (menos 5, 1) e (1, 7) e se ramifica que passam pelos vértices (menos 2, 1) e (menos 2, menos 7) e se abrem para cima e para baixo.
    Figura 11.4.22
    Exercício\(\PageIndex{8}\)

    Gráfico\(\frac{(y+2)^{2}}{9}-\frac{(x+2)^{2}}{9}=1\).

    Responda
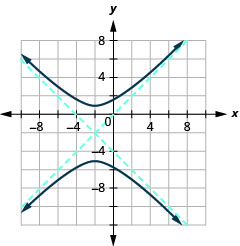
    O gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos não marcados, com um centro em (menos 2, menos 2), uma assíntota que passa por (menos 5, menos 5) e (1, 1) e uma assíntota que passa por (menos 5, 1) e (1, menos 5), e ramificações que passam pelos vértices (menos 2, 1) e (menos 2, menos 5) e se abrem para cima e para baixo.
    Figura 11.4.23

    Novamente, às vezes temos que colocar a equação na forma padrão como nosso primeiro passo.

    Exemplo\(\PageIndex{5}\)

    Escreva a equação em formato padrão e gráfico\(4 x^{2}-9 y^{2}-24 x-36 y-36=0\).

    Solução:

      .
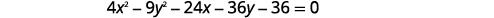    Para chegar ao formulário padrão, preencha os quadrados. .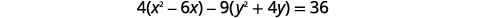
      .
      .
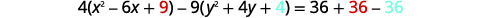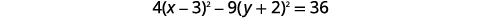    Divida cada termo por\(36\) para que a constante seja\(1\). .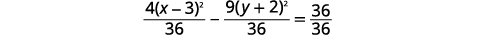
      .
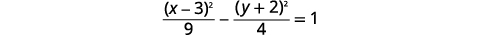    Como o\(x^{2}\) termo -é positivo, a hipérbole se abre para a esquerda e para a direita.  
    Encontre o centro,\((h,k)\). Centro:\((3, -2)\)
    Encontre\(a,b\).

    \(a=3\)

    \(b=4\)
    Desenhe o retângulo que passa pelas\(3\) unidades de pontos à esquerda/direita do centro e\(2\) unidades acima e abaixo do centro.
    Desenhe as assíntotas — as linhas nas diagonais do retângulo.
    Marque os vértices.
    Faça um gráfico dos galhos.    		 .
    Tabela 11.4.7
    Exercício\(\PageIndex{9}\)
    1. Escreva a equação na forma padrão e
    2. Gráfico\(9 x^{2}-16 y^{2}+18 x+64 y-199=0\).
    Responda
    1. \(\frac{(x+1)^{2}}{16}-\frac{(y-2)^{2}}{9}=1\)
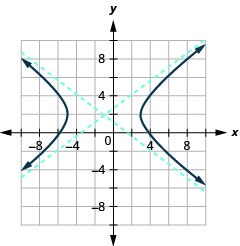
    O gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulo, com o centro (menos 1, 2), uma assíntota que passa por (menos 5, 5) e (3, menos 1) e uma assíntota que passa por (3, 5) e (menos 5, menos 1) e ramificações que passe pelos vértices (menos 5, 2) e (3, 2) e abre para a esquerda e para a direita.
    Figura 11.4.31
    Exercício\(\PageIndex{10}\)
    1. Escreva a equação na forma padrão e
    2. Gráfico\(16 x^{2}-25 y^{2}+96 x-50 y-281=0\).
    Responda
    1. \(\frac{(x+3)^{2}}{25}-\frac{(y+1)^{2}}{16}=1\)
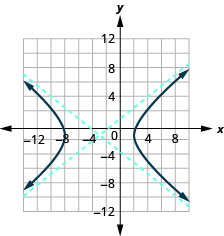
    O gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulo, com o centro (menos 3, menos 1), uma assíntota que passa por (menos 8, menos 5) e (2, 3) e uma assíntota que passa por (menos 8, 3) e (2, menos 5) e uma assíntota que passa por (menos 8, 3) e (2, menos 5) e ramificações que passam pelos vértices (menos 8, menos 1) e (2, menos 1) e se abrem à esquerda e à direita.
    Figura 11.4.32

    Identifique seções cônicas por suas equações

    Agora que concluímos nosso estudo das seções cônicas, examinaremos as diferentes equações e reconheceremos algumas maneiras de identificar uma cônica por sua equação. Quando recebemos uma equação para representar graficamente, é útil identificar a cônica para que saibamos quais os próximos passos a serem dados.

    Para identificar uma cônica a partir de sua equação, é mais fácil colocar os termos variáveis em um lado da equação e as constantes no outro.

    Cônico Características de\(x^{2}\) - e\(y^{2}\) -termos Exemplo
    Parábola \ (x^ {2}\) - e\(y^{2}\) -terms">OU\(x^{2}\) OU\(y^{2}\). Somente uma variável é quadrada. \(x=3 y^{2}-2 y+1\)
    Círculo \ (x^ {2}\) - e\(y^{2}\) -terms">\(x^{2}\) - e\(y^{2}\) - termos têm os mesmos coeficientes. \(x^{2}+y^{2}=49\)
    Elipse \ (x^ {2}\) - e\(y^{2}\) -terms">\(x^{2}\) - e\(y^{2}\) - termos têm o mesmo sinal, coeficientes diferentes. \(4 x^{2}+25 y^{2}=100\)
    Hyperbole \ (x^ {2}\) - e\(y^{2}\) -terms">\(x^{2}\)\(y^{2}\) - e - termos têm sinais diferentes, coeficientes diferentes. \(25 y^{2}-4 x^{2}=100\)
    Tabela 11.4.8
    Exemplo\(\PageIndex{6}\)

    Identifique o gráfico de cada equação como um círculo, parábola, elipse ou hipérbole.

    1. \(9 x^{2}+4 y^{2}+56 y+160=0\)
    2. \(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)
    3. \(x^{2}+y^{2}-6 x-8 y=0\)
    4. \(y=-2 x^{2}-4 x-5\)

    Solução:

    a. Os\(y^{2}\) termos\(x^{2}\) - e -têm o mesmo sinal e coeficientes diferentes.

    \(9 x^{2}+4 y^{2}+56 y+160=0\)

    Elipse

    b. Os\(y^{2}\) termos\(x^{2}\) - e -têm sinais e coeficientes diferentes.

    \(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)

    Hyperbole

    c. Os\(y^{2}\) termos\(x^{2}\) - e -têm os mesmos coeficientes.

    \(x^{2}+y^{2}-6 x-8 y=0\)

    Círculo

    d. Somente uma variável,\(x\), é quadrada.

    \(y=-2 x^{2}-4 x-5\)

    Parábola

    Exercício\(\PageIndex{11}\)

    Identifique o gráfico de cada equação como um círculo, parábola, elipse ou hipérbole.

    1. \(x^{2}+y^{2}-8 x-6 y=0\)
    2. \(4 x^{2}+25 y^{2}=100\)
    3. \(y=6 x^{2}+2 x-1\)
    4. \(16 y^{2}-9 x^{2}=144\)
    Responda
    1. Círculo
    2. Elipse
    3. Parábola
    4. Hyperbole
    Exercício\(\PageIndex{12}\)

    Identifique o gráfico de cada equação como um círculo, parábola, elipse ou hipérbole.

    1. \(16 x^{2}+9 y^{2}=144\)
    2. \(y=2 x^{2}+4 x+6\)
    3. \(x^{2}+y^{2}+2 x+6 y+9=0\)
    4. \(4 x^{2}-16 y^{2}=64\)
    Responda
    1. Elipse
    2. Parábola
    3. Círculo
    4. Hyperbole

    Acesse esses recursos on-line para obter instruções adicionais e praticar com hipérboles.

    • Faça um gráfico de uma hipérbole com o centro na origem
    • Faça um gráfico de uma hipérbole com o centro não na origem
    • Faça um gráfico de uma hipérbole em forma geral
    • Identificação de seções cônicas em formato geral

    Conceitos-chave

    • Hipérbole: Uma hipérbole são todos os pontos em um plano em que a diferença de suas distâncias de dois pontos fixos é constante.
    A figura mostra um cone circular direito de dupla soneca cortado por um plano paralelo ao eixo vertical do cone formando uma hipérbole. A figura é rotulada como 'hipérbola'.
    Figura 11.4.1
    • Cada um dos pontos fixos é chamado de foco da hipérbole.
      A linha que passa pelos focos é chamada de eixo transversal.
      Os dois pontos em que o eixo transversal cruza a hipérbole são, cada um, um vértice da hipérbole.
      O ponto médio do segmento que une os focos é chamado de centro da hipérbole.
      A linha perpendicular ao eixo transversal que passa pelo centro é chamada de eixo conjugado.
      Cada pedaço do gráfico é chamado de ramo da hipérbole.
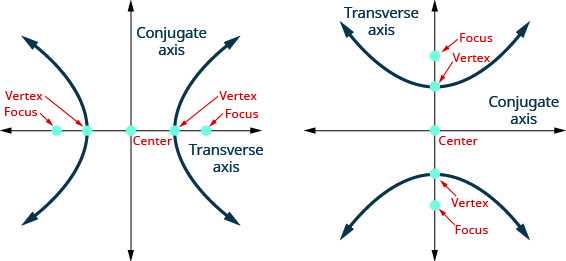
      A figura mostra dois gráficos de uma hipérbole. O primeiro gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulos. O centro da hipérbole é a origem. Os vértices e focos são mostrados com pontos que estão no eixo transversal, que é o eixo x. Os galhos passam pelos vértices e se abrem para a esquerda e para a direita. O eixo y é o eixo conjugado. O segundo gráfico mostra os eixos x e y que correm nas direções negativa e positiva, mas em intervalos sem rótulos. O centro da hipérbole é a origem. Os vértices e focos são mostrados com pontos que estão no eixo transversal, que é o eixo y. Os galhos passam pelos vértices e se abrem para cima e para baixo. O eixo x é o eixo conjugado.

    Figura 11.4.2

    Formas padrão da equação: uma hipérbole com centro\((0,0)\)

    \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)
    Orientação \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">Eixo transversal no\(x\) eixo.
    Abre à esquerda e à direita    		 \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">Eixo transversal no\(y\) eixo.
    Abre para cima e para baixo
    Vértices \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\)
    \(x\)-intercepta \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\((-a, 0),(a, 0)\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">nenhum
    \(y\)-intercepta \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">nenhum \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\((0,-a),(0, a)\)
    Retângulo \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">Usar\(( \pm a, 0)(0, \pm b)\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">Usar\((0, \pm a)( \pm b, 0)\)
    Assíntotas \ (\ frac {x^ {2}} {a^ {2}} -\ frac {y^ {2}} {b^ {2}} =1\) ">\(y=\frac{b}{a} x, y=-\frac{b}{a} x\) \ (\ frac {y^ {2}} {a^ {2}} -\ frac {x^ {2}} {b^ {2}} =1\) ">\(y=\frac{a}{b} x, y=-\frac{a}{b} x\)
    Tabela 11.4.1
    • Como representar graficamente uma hipérbole centrada em\((0,0)\).
      1. Escreva a equação na forma padrão.
      2. Determine se o eixo transversal é horizontal ou vertical.
      3. Encontre os vértices.
      4. Desenhe o retângulo centrado na origem cruzando um eixo em\(±a\) e o outro em\(±b\).
      5. Desenhe as assíntotas — as linhas nas diagonais do retângulo.
      6. Desenhe os dois ramos da hipérbole.

    Formas padrão da equação: uma hipérbole com centro\((h,k)\)

    \(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) \(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\)
    Orientação \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">O eixo transversal é horizontal. Abre à esquerda e à direita \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">O eixo transversal é vertical. Abre para cima e para baixo
    Centro \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">\((h,k)\) \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">\((h,k)\)
    Vértices \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">\(a\) unidades à esquerda e à direita do centro \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">\(a\) unidades acima e abaixo do centro
    Retângulo \ (\ frac {(x-h) ^ {2}} {a^ {2}} -\ frac {(y-k) ^ {2}} {b^ {2}} =1\) ">Use\(a\) unidades à esquerda/direita das\(b\) unidades centrais acima/abaixo do centro \ (\ frac {(y-k) ^ {2}} {a^ {2}} -\ frac {(x-h) ^ {2}} {b^ {2}} =1\) ">Use\(a\) unidades acima/abaixo das\(b\) unidades centrais à esquerda/direita do centro
    Tabela 11.4.4
    • Como representar graficamente uma hipérbole centrada em\((h,k)\).
      1. Escreva a equação na forma padrão.
      2. Determine se o eixo transversal é horizontal ou vertical.
      3. Encontre o centro\(a,b\) e.
      4. Desenhe o retângulo centrado em\((h,k)\) usar\(a,b\).
      5. Desenhe as assíntotas — as linhas nas diagonais do retângulo. Marque os vértices.
      6. Desenhe os dois ramos da hipérbole.
    Cônico Características de\(x^{2}\) - e\(y^{2}\) -termos Exemplo
    Parábola \ (x^ {2}\) - e\(y^{2}\) -terms">OU\(x^{2}\) OU\(y^{2}\). Somente uma variável é quadrada. \(x=3 y^{2}-2 y+1\)
    Círculo \ (x^ {2}\) - e\(y^{2}\) -terms">\(x^{2}\) - e\(y^{2}\) - termos têm os mesmos coeficientes. \(x^{2}+y^{2}=49\)
    Elipse \ (x^ {2}\) - e\(y^{2}\) -terms">\(x^{2}\) - e\(y^{2}\) - termos têm o mesmo sinal, coeficientes diferentes. \(4 x^{2}+25 y^{2}=100\)
    Hyperbole \ (x^ {2}\) - e\(y^{2}\) -terms">\(x^{2}\)\(y^{2}\) - e - termos têm sinais diferentes, coeficientes diferentes. \(25 y^{2}-4 x^{2}=100\)
    Tabela 11.4.8

    Glossário

    hipérbole
    Uma hipérbole é definida como todos os pontos em um plano em que a diferença de suas distâncias de dois pontos fixos é constante.