11.4: Elipses

Objetivos de

Ao final desta seção, você poderá:

• Faça um gráfico de uma elipse com centro na origem
• Encontre a equação de uma elipse com centro na origem
• Faça um gráfico de uma elipse com o centro não na origem
• Resolva a aplicação com elipses

Antes de começar, faça este teste de prontidão.

1. Gráfico$y=(x-1)^{2}-2$ usando transformações.
   Se você perdeu esse problema, consulte o Exemplo 9.57.
2. Complete o quadrado:$x^{2}-8 x=8$.
   Se você perdeu esse problema, consulte o Exemplo 9.12.
3. Escreva em formato padrão. $y=2 x^{2}-12 x+14$
   Se você perdeu esse problema, consulte o Exemplo 9.59.

Faça um gráfico de uma elipse com o centro na origem

A próxima seção cônica que veremos é uma elipse. Definimos uma elipse como todos os pontos em um plano onde a soma das distâncias de dois pontos fixos é constante. Cada um dos pontos fornecidos é chamado de foco da elipse.

Definição$\PageIndex{1}$

Uma elipse são todos os pontos em um plano em que a soma das distâncias de dois pontos fixos é constante. Cada um dos pontos fixos é chamado de foco da elipse.

Figura 11.3.1

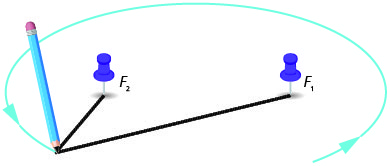
Podemos desenhar uma elipse pegando um comprimento fixo de corda flexível e prendendo as pontas a duas tachinhas. Usamos uma caneta para esticar a corda e girá-la em torno das duas tachinhas. A figura resultante é uma elipse.

Figura 11.3.2

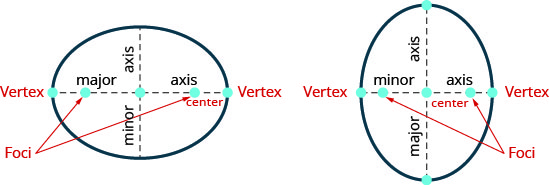
Uma linha traçada através dos focos cruza a elipse em dois pontos. Cada ponto é chamado de vértice da elipse. O segmento que conecta os vértices é chamado de eixo principal. O ponto médio do segmento é chamado de centro da elipse. Um segmento perpendicular ao eixo maior que passa pelo centro e cruza a elipse em dois pontos é chamado de eixo menor.

Figura 11.3.3

Mencionamos anteriormente que nosso objetivo é conectar a geometria de uma cônica com a álgebra. Colocar a elipse em um sistema de coordenadas retangulares nos dá essa oportunidade. Na figura, colocamos a elipse de forma que os focos$((−c,0),(c,0))$ fiquem no$x$ eixo -e o centro seja a origem.

Figura 11.3.4

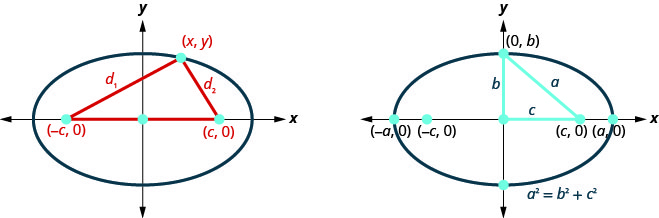
A definição afirma que a soma da distância dos focos até um ponto$(x,y)$ é constante. Então$d_{1}+d_{2}$ é uma constante que chamaremos$2a$ assim,$d_{1}+d_{2}=2 a$. Usaremos a fórmula da distância para nos levar a uma fórmula algébrica para uma elipse.

$d_{1} \quad+\quad \quad d_{2} \quad=\quad 2 a$

Use a fórmula da distância para encontrar$d_{1},d_{2}$.

$\sqrt{(x-(-c))^{2}+(y-0)^{2}}+\sqrt{(x-c)^{2}+(y-0)^{2}}=2 a$

Depois de eliminar os radicais e simplificar, obtemos:

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{a^{2}-c^{2}}=1$

Para simplificar a equação da elipse, deixamos$a^{2}−c^{2}=b^{2}$ .So, a equação de uma elipse centrada na origem na forma padrão é:

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$

Para representar graficamente a elipse, será útil conhecer as interceptações. Encontraremos os$x$ -interceptos e$y$ -interceptos usando a fórmula.

$y$-intercepta

Deixe$x=0$.

$\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1 \\ \frac{0^{2}}{a^{2}}+\frac{y^{2}}{a^{2}} &=1 \\ \frac{y^{2}}{b^{2}} &=1 \\ y^{2} &=b^{2} \\ y &=\pm b \end{aligned}$

As$y$ interceptações -são$(0,b)$$(0, -b)$ e.

$x$-intercepta

Deixe$y=0$.

$\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}}+\frac{0^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}} &=1 \\ x^{2} &=a^{2} \\ x &=\pm a \end{aligned}$

As$x$ interceptações -são$(a,0)$$(-a,0)$ e.

Definição$\PageIndex{2}$

Forma padrão da equação: uma elipse com centro$(0,0)$

A forma padrão da equação de uma elipse com centro$(0,​​0)$ é

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$

As$x$ interceptações -são$(a,0)$$(−a,0)$ e.

As$y$ interceptações -são$(0,b)$$(0,−b)$ e.

Figura 11.3.5

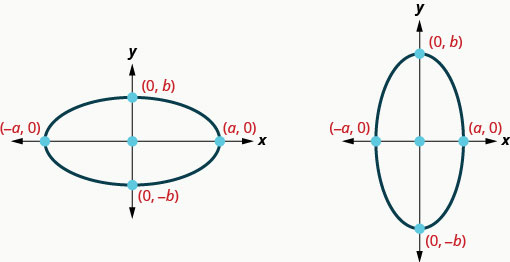
Observe que quando o eixo principal é horizontal, o valor de$a$ será maior que o valor de$b$ e quando o eixo principal for vertical, o valor de$b$ será maior que o valor de$a$. Usaremos essas informações para representar graficamente uma elipse centrada na origem.

Elipse com centro$(0,0)$

Tabela 11.3.1

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$	$a>b$	$b>a$
Eixo principal	no$x$ eixo -.	no$y$ eixo -
$x$-intercepta	$(-a, 0),(a, 0)$
$y$-intercepta	$(0,-b),(0, b)$

Exemplo$\PageIndex{1}$

Gráfico:$\frac{x^{2}}{4}+\frac{y^{2}}{9}=1$.

Solução:

Tabela 11.3.2

Etapa 1. Escreva a equação na forma padrão.	Está na forma padrão.	$\frac{x^{2}}{4}+\frac{y^{2}}{9}=1$
Etapa 2. Determine se o eixo principal é horizontal ou vertical.	Como$9>4$ e$9$ está no$y^{2}$ termo, o eixo principal é vertical.	O eixo principal é vertical.
Etapa 3. Encontre as extremidades do eixo principal.	Os pontos finais serão os$y$ interceptos. Desde$b^{2}=9$ então$b=\pm 3$. Os pontos finais do eixo principal são$(0,3),(0,-3)$.	Os pontos finais do eixo principal são$(0,3),(0,-3)$.
Etapa 4. Encontre as extremidades do eixo menor.	Os pontos finais serão os$x$ interceptos. Desde$a^{2}=4$ então$a=\pm 2$. Os pontos finais do eixo principal são$(2,0),(-2,0)$.	Os pontos finais do eixo principal são$(2,0),(-2,0)$.
Etapa 5. Esboce a elipse.

Exercício$\PageIndex{1}$

Gráfico:$\frac{x^{2}}{4}+\frac{y^{2}}{16}=1$.

Resposta

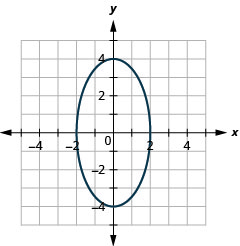
Figura 11.3.7

Exercício$\PageIndex{2}$

Gráfico:$\frac{x^{2}}{9}+\frac{y^{2}}{16}=1$.

Resposta

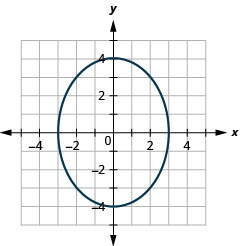
Figura 11.3.8

Resumimos as etapas para referência.

COMO REPRESENTAR GRAFICAMENTE UMA ELIPSE COM O CENTRO$(0,0)$.

1. Escreva a equação na forma padrão.
2. Determine se o eixo principal é horizontal ou vertical.
3. Encontre as extremidades do eixo principal.
4. Encontre os pontos finais do eixo menor
5. Esboce a elipse.

Às vezes, nossa equação primeiro precisa ser colocada na forma padrão.

Exemplo$\PageIndex{2}$

Gráfico$x^{2}+4 y^{2}=16$.

Solução:

Tabela 11.3.3

Reconhecemos isso como a equação de uma elipse, pois os$y$ termos$x$ e são quadrados e têm coeficientes diferentes.	$x^{2}+4 y^{2}=16$
Para obter a equação na forma padrão, divida os dois lados$16$ por para que a equação seja igual$1$ a.	$\frac{x^{2}}{16}+\frac{4 y^{2}}{16}=\frac{16}{16}$
Simplifique.	$\frac{x^{2}}{16}+\frac{y^{2}}{4}=1$
A equação está na forma padrão. A elipse está centrada na origem.	O centro é$(0,0)$.
Como$16>4$ e$16$ está no$x^{2}$ termo, o eixo principal é horizontal.
$a^{2}=16, a=\pm 4$ $b^{2}=4, \quad b=\pm 2$	Os vértices são$(4,0),(−4,0)$. Os pontos finais do eixo menor são $(0,2),(0,−2)$.
Esboce a parábola.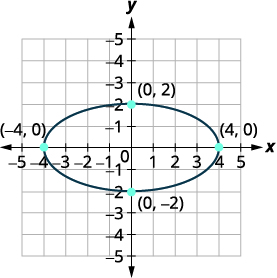

Exercício$\PageIndex{3}$

Gráfico$9 x^{2}+16 y^{2}=144$.

Resposta

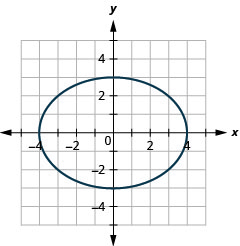
Figura 11.3.10

Exercício$\PageIndex{4}$

Gráfico$16 x^{2}+25 y^{2}=400$.

Resposta

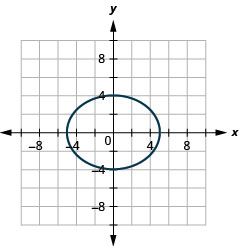
Figura 11.3.11

Encontre a equação de uma elipse com o centro na origem

Se recebermos o gráfico de uma elipse, podemos encontrar a equação da elipse.

Exemplo$\PageIndex{3}$

Encontre a equação da elipse mostrada.

Figura 11.3.12

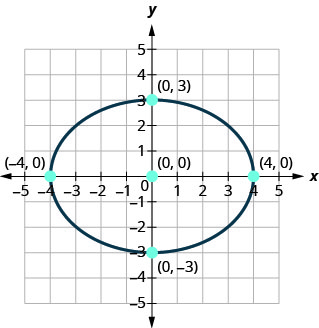
Solução:

Nós reconhecemos isso como uma elipse centrada na origem.

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$

Como o eixo principal é horizontal e a distância do centro ao vértice é$4$, nós sabemos$a=4$ e assim$a^{2}=16$.

$\frac{x^{2}}{16}+\frac{y^{2}}{b^{2}}=1$

O eixo menor é vertical e a distância do centro até a elipse é$3$, nós sabemos$b=3$ e assim por diante$b^{2}=9$.

$\frac{x^{2}}{16}+\frac{y^{2}}{9}=1$

Exercício$\PageIndex{5}$

Encontre a equação da elipse mostrada.

Figura 11.3.13

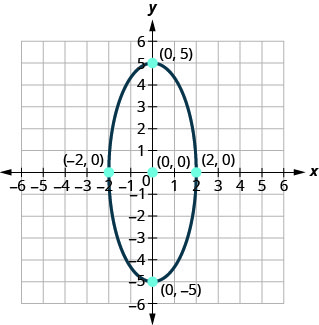
Resposta

$\frac{x^{2}}{4}+\frac{y^{2}}{25}=1$

Exercício$\PageIndex{6}$

Encontre a equação da elipse mostrada.

Figura 11.3.14

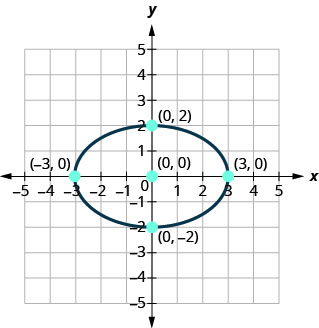
Resposta

$\frac{x^{2}}{9}+\frac{y^{2}}{4}=1$

Faça um gráfico de uma elipse com o centro fora da origem

As elipses que observamos até agora estão todas centradas na origem. Agora veremos as elipses cujo centro é$(h,k)$.

A equação é$\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$ e quando$a>b$, o eixo principal é horizontal, então a distância do centro ao vértice é$a$. Quando$b>a$, o eixo principal é vertical, então a distância do centro até o vértice é$b$.

Definição$\PageIndex{3}$

Forma padrão da equação: uma elipse com centro$(h,k)$

A forma padrão da equação de uma elipse com centro$(h,k)$ é

$\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$

Quando$a>b$, o eixo principal é horizontal, então a distância do centro até o vértice é$a$.

Quando$b>a$, o eixo principal é vertical, então a distância do centro até o vértice é$b$.

Exemplo$\PageIndex{4}$

Gráfico:$\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1$.

Solução:

Tabela 11.3.4

A equação está na forma padrão,$\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$.	$\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1$
A elipse está centrada em$(h,k)$.	O centro é$(3,1)$.
Como$9>4$ e$9$ está no$x^{2}$ termo, o eixo principal é horizontal.
$a^{2}=9, a=\pm 3$ $b^{2}=4, b=\pm 2$	A distância do centro aos vértices é$3$. A distância do centro até as extremidades do eixo menor é$2$.
Esboce a elipse.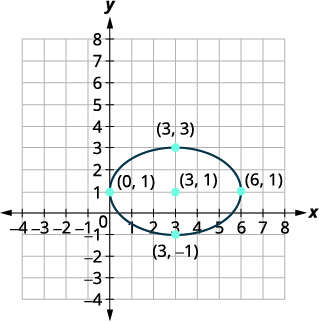

Exercício$\PageIndex{7}$

Gráfico:$\frac{(x+3)^{2}}{4}+\frac{(y-5)^{2}}{16}=1$.

Resposta

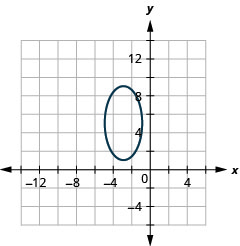
Figura 11.3.16

Exercício$\PageIndex{8}$

Gráfico:$\frac{(x-1)^{2}}{25}+\frac{(y+3)^{2}}{16}=1$.

Resposta

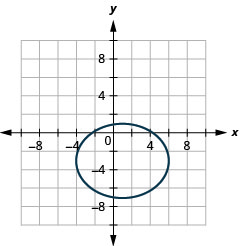
Figura 11.3.17

Se observarmos as equações de$\frac{x^{2}}{9}+\frac{y^{2}}{4}=1$ e$\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1$, veremos que ambas são elipses com$a=3$$b=2$ e. Então, eles terão o mesmo tamanho e forma. Eles são diferentes porque não têm o mesmo centro.

Figura 11.3.18

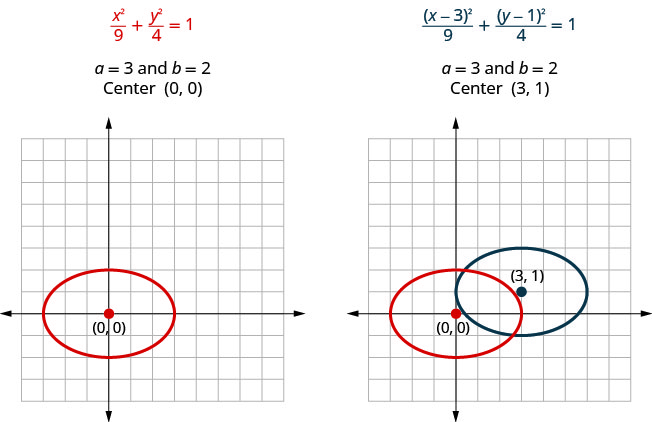
Observe no gráfico acima que poderíamos ter representado graficamente$\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1$ por traduções. Movemos a elipse original para as$3$ unidades certas e depois para cima$1$.

Figura 11.3.19

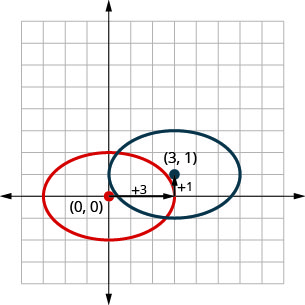
No próximo exemplo, usaremos o método de tradução para representar graficamente a elipse.

Exemplo$\PageIndex{5}$

Gráfico$\frac{(x+4)^{2}}{16}+\frac{(y-6)^{2}}{9}=1$ por tradução.

Solução:

Essa elipse terá o mesmo tamanho e forma de$\frac{x^{2}}{16}+\frac{y^{2}}{9}=1$ quem está o centro$(0,0)$. Primeiro, representamos graficamente essa elipse.

Tabela 11.3.5

O centro é$(0,0)$.	Centro$(0,0)$
Desde então$16>9$, o eixo principal é horizontal.
$a^{2}=16, a=\pm 4$ $b^{2}=9, \quad b=\pm 3$	Os vértices são$(4,0),(−4,0)$. Os pontos finais do eixo menor são $(0,3),(0,−3)$.
Esboce a elipse.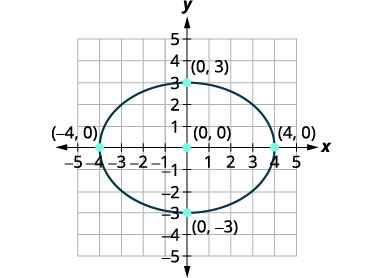
A equação original está na forma padrão,$\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$.	$\frac{(x-(-4))^{2}}{16}+\frac{(y-6)^{2}}{9}=1$
A elipse está centrada em$(h,k)$.	O centro é$(-4,6)$.
Traduzimos o gráfico de$\frac{x^{2}}{16}+\frac{y^{2}}{9}=1$ quatro unidades para a esquerda e depois para cima$6$. Verifique se o centro está$(−4,6)$. A nova elipse é a elipse cuja equação é $\frac{(x+4)^{2}}{16}+\frac{(y-6)^{2}}{9}=1$.

Exercício$\PageIndex{9}$

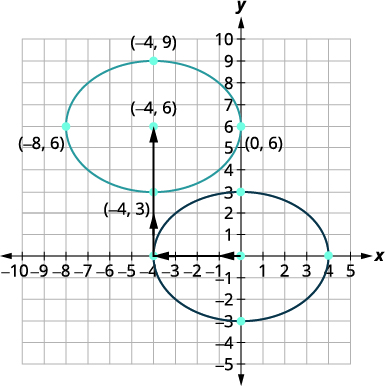Gráfico$\frac{(x-5)^{2}}{9}+\frac{(y+4)^{2}}{4}=1$ por tradução.

Resposta

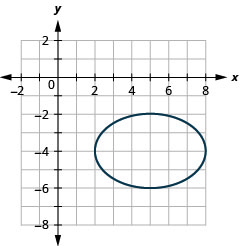
Figura 11.3.22

Exercício$\PageIndex{10}$

Gráfico$\frac{(x+6)^{2}}{16}+\frac{(y+2)^{2}}{25}=1$ por tradução.

Resposta

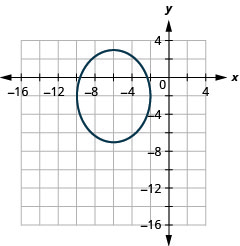
Figura 11.3.23

Quando uma equação tem um$x^{2}$ e a$y^{2}$ com coeficientes diferentes, verificamos se é uma elipse colocando-a na forma padrão. Em seguida, poderemos representar graficamente a equação.

Exemplo$\PageIndex{6}$

Escreva a equação$x^{2}+4 y^{2}-4 x+24 y+24=0$ em formato padrão e gráfico.

Solução:

Colocamos a equação na forma padrão completando os quadrados em$x$$y$ e.

Tabela 11.3.6

	$x^{2}+4 y^{2}-4 x+24 y+24=0$
Reescreva o agrupamento dos$x$ termos e$y$ termos.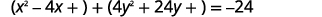
Faça com que os coeficientes sejam$y^{2}$ iguais$x^{2}$ e iguais$1$.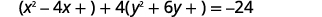
Complete os quadrados.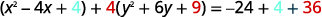
Escreva como quadrados binomiais.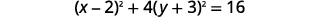
Divida os dois lados por$16$ para ir para a$1$ direita.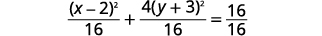
Simplifique.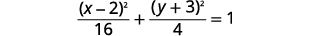
A equação está na forma padrão,$\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$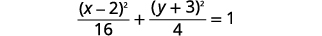
A elipse está centrada em$(h,k)$.	O centro é$(2,-3)$.
Como$16>4$ e$16$ está no$x^{2}$ termo, o eixo principal é horizontal. $a^{2}=16, a=\pm 4$ $b^{2}=4, \quad b=\pm 2$	A distância do centro aos vértices é$4$. A distância do centro até as extremidades do eixo menor é$2$.
Esboce a elipse.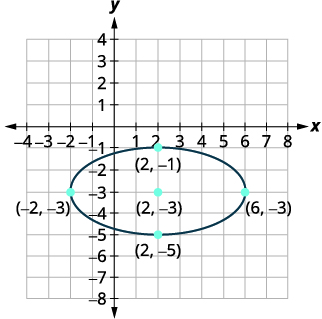

Exercício$\PageIndex{11}$

1. Escreva a equação$6 x^{2}+4 y^{2}+12 x-32 y+34=0$ na forma padrão e
2. Gráfico.

Resposta

1. $\frac{(x+1)^{2}}{6}+\frac{(y-4)^{2}}{9}=1$

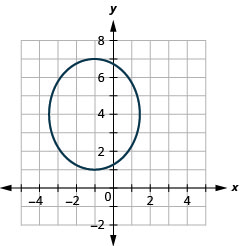
Figura 11.3.32

Exercício$\PageIndex{12}$

1. Escreva a equação$4 x^{2}+y^{2}-16 x-6 y+9=0$ na forma padrão e
2. Gráfico.

Resposta

1. $\frac{(x-2)^{2}}{4}+\frac{(y-3)^{2}}{16}=1$

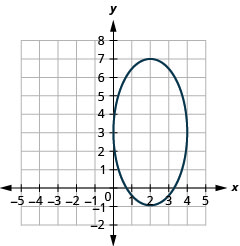
Figura 11.3.33

Resolva aplicações com elipses

As órbitas dos planetas ao redor do sol seguem caminhos elípticos.

Exemplo$\PageIndex{7}$

Plutão (um planeta anão) se move em uma órbita elíptica ao redor do Sol. O mais próximo que Plutão chega do Sol é de aproximadamente unidades$30$ astronômicas (UA) e o mais distante é aproximadamente$50$ UA. O Sol é um dos focos da órbita elíptica. Deixando a elipse centrar na origem e rotulando os eixos em AU, a órbita ficará parecida com a figura abaixo. Use o gráfico para escrever uma equação para a órbita elíptica de Plutão.

Figura 11.3.34

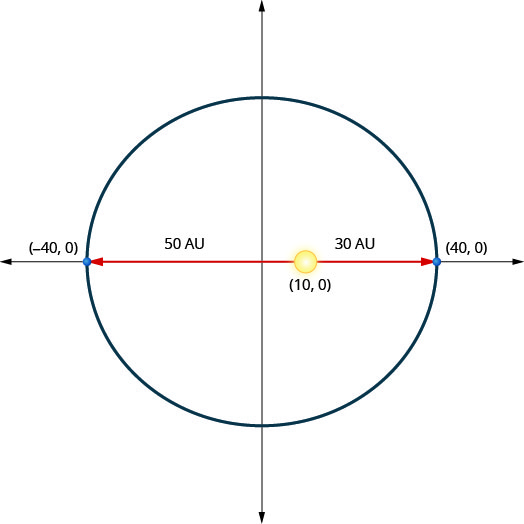
Solução:

Nós reconhecemos isso como uma elipse centrada na origem.

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$

Como o eixo principal é horizontal e a distância do centro ao vértice é$40$, nós sabemos$a=40$ e assim$a^{2}=1600$.

$\frac{x^{2}}{1600}+\frac{y^{2}}{b^{2}}=1$

O eixo menor é vertical, mas os pontos finais não são fornecidos. Para descobrir,$b$ usaremos a localização do Sol. Como o Sol é o foco da elipse no ponto$(10,0)$, nós sabemos$c=10$. Use isso para resolver$b^{2}$.

$b^{2}=a^{2}-c^{2}$
$b^{2}=40^{2}-10^{2}$
$b^{2}=1600-100$
$b^{2}=1500$

Substitua$a^{2}$ e$b^{2}$ na forma padrão da elipse.

$\frac{x^{2}}{1600}+\frac{y^{2}}{1500}=1$

Exercício$\PageIndex{13}$

Um planeta se move em uma órbita elíptica ao redor do sol. O mais próximo que o planeta chega do sol é aproximadamente$20$ AU e o mais distante é aproximadamente$30$ AU. O sol é um dos focos da órbita elíptica. Deixando a elipse centrar na origem e rotulando os eixos em AU, a órbita ficará parecida com a figura abaixo. Use o gráfico para escrever uma equação para a órbita elíptica do planeta.

Figura 11.3.35

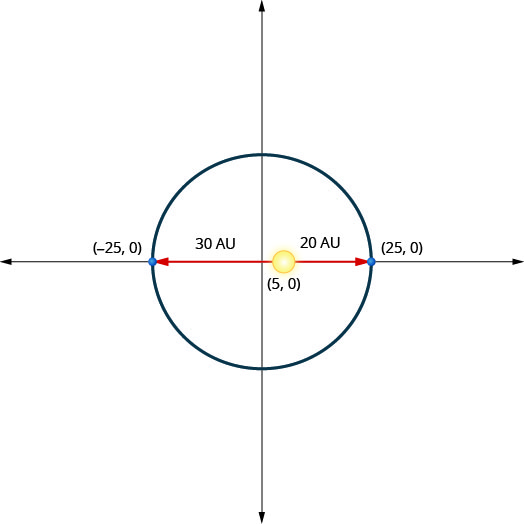
Resposta

$\frac{x^{2}}{625}+\frac{y^{2}}{600}=1$

Exercício$\PageIndex{14}$

Um planeta se move em uma órbita elíptica ao redor do sol. O mais próximo que o planeta chega do sol é aproximadamente$20$ AU e o mais distante é aproximadamente$50$ AU. O sol é um dos focos da órbita elíptica. Deixando a elipse centrar na origem e rotulando os eixos em AU, a órbita ficará parecida com a figura abaixo. Use o gráfico para escrever uma equação para a órbita elíptica do planeta.

Figura 11.3.36

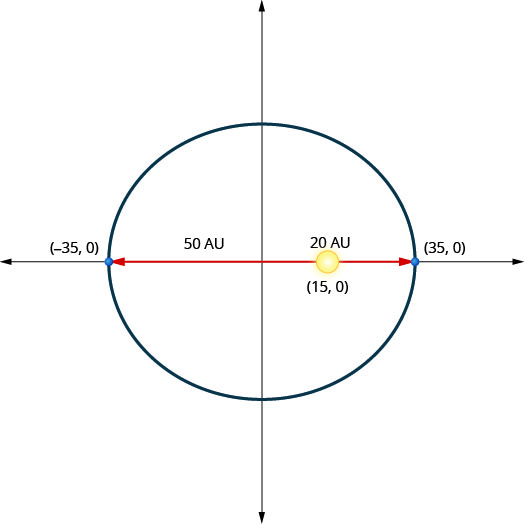
Resposta

$\frac{x^{2}}{1225}+\frac{y^{2}}{1000}=1$

Acesse esses recursos on-line para obter instruções adicionais e praticar com elipses.

• Seções cônicas: representação gráfica de elipses, parte 1
• Seções cônicas: representação gráfica de elipses, parte 2
• Equação para elipse a partir do gráfico

Conceitos-chave

• Elipse: Uma elipse são todos os pontos em um plano em que a soma das distâncias de dois pontos fixos é constante. Cada um dos pontos fixos é chamado de foco da elipse.
  

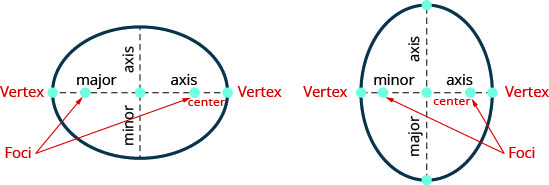
Figura 11.3.37

• Se traçarmos uma linha através dos focos, cruzamos a elipse em dois pontos — cada um é chamado de vértice da elipse.
  O segmento que conecta os vértices é chamado de eixo principal.
  O ponto médio do segmento é chamado de centro da elipse.
  Um segmento perpendicular ao eixo maior que passa pelo centro e cruza a elipse em dois pontos é chamado de eixo menor.
• Forma padrão da equação uma elipse com centro$(0,0)$: A forma padrão da equação de uma elipse com centro$(0,0)$, é

  $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$

  As$x$ interceptações -são$(a,0)$$(−a,0)$ e.
  As$y$ interceptações -são$(0,b)$$(0,−b)$ e.
• Como fazer uma elipse com centro$(0,0)$
  1. Escreva a equação na forma padrão.
  2. Determine se o eixo principal é horizontal ou vertical.
  3. Encontre as extremidades do eixo principal.
  4. Encontre os pontos finais do eixo menor
  5. Esboce a elipse.
• Forma padrão da equação uma elipse com centro$(h,k)$: A forma padrão da equação de uma elipse com centro$(h,k)$, é

  $\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$

  Quando$a>b$, o eixo principal é horizontal, então a distância do centro até o vértice é$a$.
  Quando$b>a$, o eixo principal é vertical, então a distância do centro até o vértice é$b$.

Glossário

elipse

Uma elipse são todos os pontos em um plano em que a soma das distâncias de dois pontos fixos é constante.