8.7: Resolver equações radicais
- Page ID
- 183424
Ao final desta seção, você poderá:
- Resolva equações radicais
- Resolva equações radicais com dois radicais
- Use radicais em aplicações
Antes de começar, faça este teste de prontidão.
- Simplifique:\((y−3)^{2}\).
Se você perdeu esse problema, consulte o Exemplo 5.31. - Resolver:\(2x−5=0\).
Se você perdeu esse problema, revise o Exemplo 2.2. - Resolver\(n^{2}−6n+8=0\).
Se você perdeu esse problema, consulte o Exemplo 6.45.
Resolva equações radicais
Nesta seção, resolveremos equações que têm uma variável no radicando de uma expressão radical. Uma equação desse tipo é chamada de equação radical.
Definição\(\PageIndex{1}\)
Uma equação na qual uma variável está no radicando de uma expressão radical é chamada de equação radical.
Como de costume, ao resolver essas equações, o que fazemos em um lado de uma equação também devemos fazer no outro lado. Depois de isolarmos o radical, nossa estratégia será elevar os dois lados da equação à potência do índice. Isso eliminará o radical.
Resolver equações radicais contendo um índice par elevando ambos os lados à potência do índice pode introduzir uma solução algébrica que não seria uma solução para a equação radical original. Novamente, chamamos isso de solução estranha, como fizemos quando resolvemos equações racionais.
No próximo exemplo, veremos como resolver uma equação radical. Nossa estratégia é baseada na elevação de um radical com índice\(n\) de\(n^{th}\) potência. Isso eliminará o radical.
Para\(a \geq 0,(\sqrt[n]{a})^{n}=a\).
Resolver:\(\sqrt{5 n-4}-9=0\).
Solução:
| Etapa 1: Isole o radical em um lado da equação. |
Para isolar o radical, adicione\(9\) aos dois lados. Simplifique. |
\(\begin{array}{c}{\sqrt{5 n-4}-9=0} \\ {\sqrt{5 n-4}-9\color{red}{+9}\color{black}{=}0\color{red}{+9}} \\ {\sqrt{5 n-4}=9}\end{array}\) |
| Etapa 2: eleve os dois lados da equação até a potência do índice. | Como o índice de uma raiz quadrada é\(2\), nós quadramos os dois lados. | \((\sqrt{5 n-4})^{2}=(9)^{2}\) |
| Etapa 3: Resolva a nova equação. | Lembre-se,\((\sqrt{a})^{2}=a\). | \(\begin{aligned} 5 n-4 &=81 \\ 5 n &=85 \\ n &=17 \end{aligned}\) |
| Etapa 4: Verifique a resposta na equação original. |
Verifique a resposta. \(\begin{array}{r}{\sqrt{5 n-4}-9=0} \\ {\sqrt{5(\color{red}{17}\color{black}{)}-4}-9 \stackrel{?}{=} 0} \\ {\sqrt{85-4}-9 \stackrel{?}{=} 0} \\ {\sqrt{81}-9 \stackrel{?}{=} 0} \\ {9-9=0} \\ {0=0}\end{array}\) A solução é\(n=17\). |
Resolver:\(\sqrt{3 m+2}-5=0\).
- Resposta
-
\(m=\frac{23}{3}\)
Resolver:\(\sqrt{10 z+1}-2=0\).
- Resposta
-
\(z=\frac{3}{10}\)
Resolva uma equação radical com um radical
- Isole o radical em um lado da equação.
- Eleve os dois lados da equação até a potência do índice.
- Resolva a nova equação.
- Verifique a resposta na equação original.
Quando usamos um sinal radical, ele indica a raiz principal ou positiva. Se uma equação tiver um radical com um índice par igual a um número negativo, essa equação não terá solução.
Resolver:\(\sqrt{9 k-2}+1=0\).
Solução:
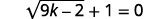 |
|
| Para isolar o radical, subtraia\(1\) para os dois lados. |  |
| Simplifique. | 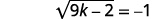 |
Como a raiz quadrada é igual a um número negativo, a equação não tem solução.
Resolver:\(\sqrt{2 r-3}+5=0\).
- Resposta
-
sem solução
Resolver:\(\sqrt{7 s-3}+2=0\).
- Resposta
-
sem solução
Se um lado de uma equação com raiz quadrada for um binômio, usamos o Padrão Produto de Quadrados Binomiais quando o quadramos.
Definição\(\PageIndex{2}\)
Quadrados binomiais
\(\begin{array}{l}{(a+b)^{2}=a^{2}+2 a b+b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}\)
Não se esqueça do meio termo!
Resolver:\(\sqrt{p-1}+1=p\).
Solução:
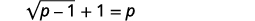 |
|
| Para isolar o radical, subtraia\(1\) dos dois lados. | 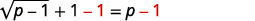 |
| Simplifique. | 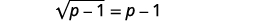 |
| Faça o quadrado dos dois lados da equação. | 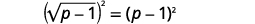 |
| Simplifique, usando o Produto do Padrão de Quadrados Binomiais à direita e resolva a nova equação. | 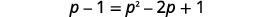 |
| É uma equação quadrática, então obtenha zero em um lado. | 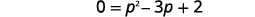 |
| Considere o lado direito. | 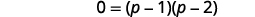 |
| Use a propriedade Zero Product. | 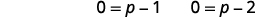 |
| Resolva cada equação. | 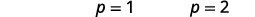 |
| Confira as respostas. | |
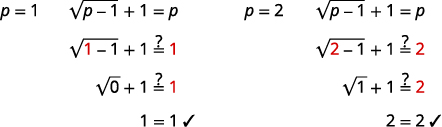 |
As soluções são\(p=1, p=2\).
Resolver:\(\sqrt{x-2}+2=x\).
- Resposta
-
\(x=2, x=3\)
Resolver:\(\sqrt{y-5}+5=y\).
- Resposta
-
\(y=5, y=6\)
Quando o índice do radical é\(3\), colocamos os dois lados em cubos para remover o radical.
\((\sqrt[3]{a})^{3}=a\)
Resolver:\(\sqrt[3]{5 x+1}+8=4\).
Solução:
| \(\sqrt[3]{5 x+1}+8=4\) | |
| Para isolar o radical, subtraia\(8\) dos dois lados. | \(\sqrt[3]{5 x+1}=-4\) |
| Cube os dois lados da equação. | \((\sqrt[3]{5 x+1})^{3}=(-4)^{3}\) |
| Simplifique. | \(5 x+1=-64\) |
| Resolva a equação. | \(5 x=-65\) |
| \(x=-13\) | |
| Verifique a resposta. | |
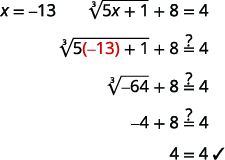 |
|
| A solução é\(x=-13\). |
Resolver:\( \sqrt[3]{4 x-3}+8=5\)
- Resposta
-
\(x=-6\)
Resolver:\(\sqrt[3]{6 x-10}+1=-3\)
- Resposta
-
\(x=-9\)
Às vezes, uma equação conterá expoentes racionais em vez de um radical. Usamos as mesmas técnicas para resolver a equação de quando temos um radical. Nós elevamos cada lado da equação à potência do denominador do expoente racional. Uma vez que\(\left(a^{m}\right)^{^{n}}=a^{m \cdot n}\), temos, por exemplo,
\(\left(x^{\frac{1}{2}}\right)^{2}=x,\left(x^{\frac{1}{3}}\right)^{3}=x\)
Lembre-se,\(x^{\frac{1}{2}}=\sqrt{x}\)\(x^{\frac{1}{3}}=\sqrt[3]{x}\) e.
Resolver:\((3 x-2)^{\frac{1}{4}}+3=5\).
Solução:
| \((3 x-2)^{\frac{1}{4}}+3=5\) | |
| Para isolar o termo com o expoente racional, subtraia\(3\) dos dois lados. | \((3 x-2)^{\frac{1}{4}}=2\) |
| Eleve cada lado da equação até a quarta potência. | \(\left((3 x-2)^{\frac{1}{4}}\right)^{4}=(2)^{4}\) |
| Simplifique. | \(3 x-2=16\) |
| Resolva a equação. | \(3x=18\) |
| \(x=6\) | |
| Verifique a resposta. | |
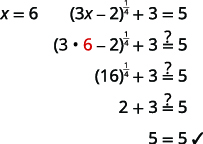 |
|
| A solução é\(x=6\). |
Resolver:\((9 x+9)^{\frac{1}{4}}-2=1\)
- Resposta
-
\(x=8\)
Resolver:\((4 x-8)^{\frac{1}{4}}+5=7\)
- Resposta
-
\(x=6\)
Às vezes, a solução de uma equação radical resulta em duas soluções algébricas, mas uma delas pode ser uma solução estranha!
Resolver:\(\sqrt{r+4}-r+2=0\).
Solução:
| \(\sqrt{r+4}-r+2=0\) | |
| Isole o radical. | \(\sqrt{r+4}=r-2\) |
| Faça o quadrado dos dois lados da equação. | \((\sqrt{r+4})^{2}=(r-2)^{2}\) |
| Simplifique e depois resolva a equação. | \(r+4=r^{2}-4 r+4\) |
| Se for uma equação quadrática, então obtenha zero em um lado. | \(0=r^{2}-5 r\) |
| Considere o lado direito. | \(0=r(r-5)\) |
| Use a propriedade Zero Product. | \(0=r \quad 0=r-5\) |
| Resolva a equação. | \(r=0 \quad r=5\) |
| Verifique sua resposta. | |
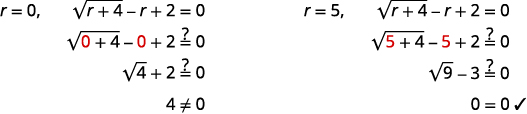 |
A solução é\(r=5\). |
| \(r=0\)é uma solução extravagante. |
Resolver:\(\sqrt{m+9}-m+3=0\)
- Resposta
-
\(m=7\)
Resolver:\(\sqrt{n+1}-n+1=0\).
- Resposta
-
\(n=3\)
Quando há um coeficiente na frente do radical, também devemos elevá-lo à potência do índice.
Resolver:\(3 \sqrt{3 x-5}-8=4\).
Solução:
| \(3 \sqrt{3 x-5}-8=4\) | |
| Isole o termo radical. | \(3 \sqrt{3 x-5}=12\) |
| Isole o radical dividindo os dois lados por\(3\). | \(\sqrt{3 x-5}=4\) |
| Faça o quadrado dos dois lados da equação. | \((\sqrt{3 x-5})^{2}=(4)^{2}\) |
| Simplifique e resolva a nova equação. | \(3 x-5=16\) |
| \(3x=21\) | |
| Resolva a equação. | \(x=7\) |
| Verifique a resposta. | |
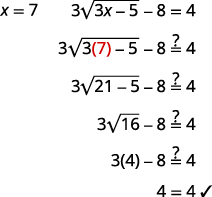 |
|
| A solução é\(x=7\). |
Resolver:\(2 \sqrt{4 a+4}-16=16\).
- Resposta
-
\(a=63\)
Resolver:\(3 \sqrt{2 b+3}-25=50\)
- Resposta
-
\(b=311\)
Resolva equações radicais com dois radicais
Se a equação radical tem dois radicais, começamos isolando um deles. Muitas vezes, é mais fácil isolar primeiro os radicais mais complicados.
No exemplo a seguir, quando um radical é isolado, o segundo radical também é isolado.
Resolver:\(\sqrt[3]{4 x-3}=\sqrt[3]{3 x+2}\).
Solução:
Os termos radicais são isolados.
\(\sqrt[3]{4 x-3}=\sqrt[3]{3 x+2}\)
Como o índice é\(3\), cube os dois lados da equação.
\((\sqrt[3]{4 x-3})^{3}=(\sqrt[3]{3 x+2})^{3}\)
Simplifique e resolva a nova equação.
\(\begin{aligned} 4 x-3 &=3 x+2 \\ x-3 &=2 \\ x &=5 \end{aligned}\)
A solução é\(x=5\).
Verifique a resposta.
Deixamos que você mostre essas\(5\) verificações!
Resolver:\(\sqrt[3]{5 x-4}=\sqrt[3]{2 x+5}\).
- Resposta
-
\(x=3\)
Resolver:\(\sqrt[3]{7 x+1}=\sqrt[3]{2 x-5}\).
- Resposta
-
\(x=-\frac{6}{5}\)
Às vezes, depois de elevar os dois lados de uma equação a uma potência, ainda temos uma variável dentro de um radical. Quando isso acontece, repetimos as etapas 1 e 2 do nosso procedimento. Isolamos o radical e elevamos os dois lados da equação à potência do índice novamente.
Resolver:\(\sqrt{m}+1=\sqrt{m+9}\).
Solução:
| Etapa 1: Isole um dos termos radicais em um lado da equação. | O radical à direita está isolado. | \(\sqrt{m}+1=\sqrt{m+9}\) |
| Etapa 2: eleve os dois lados da equação até a potência do índice. |
Nós quadramos os dois lados. Simplifique — tenha muito cuidado ao multiplicar! |
\((\sqrt{m}+1)^{2}=(\sqrt{m+9})^{2}\) |
|
Etapa 3: Existem mais radicais? Se sim, repita a Etapa 1 e a Etapa 2 novamente. Se não, resolva a nova equação. |
Ainda há um radical na equação. Portanto, devemos repetir as etapas anteriores. Isole o termo radical. Aqui, podemos isolar facilmente o radical dividindo os dois lados por\(2\). Quadrar os dois lados. |
\(\begin{aligned} m+2 \sqrt{m}+1 &=m+9 \\ 2 \sqrt{m} &=8 \\ \sqrt{m} &=4 \\(\sqrt{m})^{2} &=(4)^{2} \\ m &=16 \end{aligned}\) |
| Etapa 4: Verifique a resposta na equação original. |
\(\begin{aligned}\sqrt{m}+1&=\sqrt{m+9} \\ \sqrt{\color{red}{16}}\color{black}{+}1& \stackrel{?}{=} \sqrt{\color{red}{16}\color{black}{+}9} \\ 4+1& \stackrel{?}{=} 5 \\ 5&=5\end{aligned}\) A solução é\(m=16\). |
Resolver:\(3-\sqrt{x}=\sqrt{x-3}\).
- Resposta
-
\(x=4\)
Resolver:\(\sqrt{x}+2=\sqrt{x+16}\).
- Resposta
-
\(x=9\)
Resumimos as etapas aqui. Ajustamos nossas etapas anteriores para incluir mais de um radical na equação. Esse procedimento agora funcionará para qualquer equação radical.
Resolva uma equação radical
- Isole um dos termos radicais em um lado da equação.
- Eleve os dois lados da equação até a potência do índice.
- Existem mais radicais?
Se sim, repita a Etapa 1 e a Etapa 2 novamente.
Se não, resolva a nova equação. - Verifique a resposta na equação original.
Tenha cuidado ao quadrar binômios no próximo exemplo. Lembre-se do padrão em\((a+b)^{2}=a^{2}+2 a b+b^{2}\) ou\((a-b)^{2}=a^{2}-2 a b+b^{2}\).
Resolver:\(\sqrt{q-2}+3=\sqrt{4 q+1}\).
Solução:
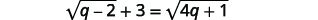 |
|
| O radical à direita está isolado. Quadrar os dois lados. | 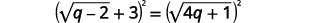 |
| Simplifique. | 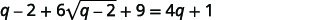 |
| Ainda há um radical na equação, então devemos repetir as etapas anteriores. Isole o radical. | 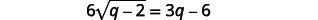 |
| Quadrar os dois lados. Não adiantaria dividir os dois lados por\(6\). Lembre-se de ajustar o quadrado entre o\(6\) e o\(\sqrt{q-2}\). | 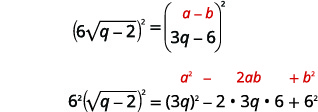 |
| Simplifique e resolva a nova equação. | 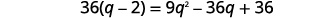 |
| Distribuir. | 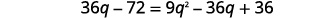 |
| É uma equação quadrática, então obtenha zero em um lado. | 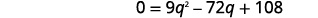 |
| Considere o lado direito. | 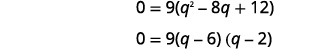 |
| Use a propriedade Zero Product. | 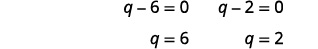 |
| Os cheques são deixados para você. | As soluções são\(q=6\)\(q=2\) e. |
Resolver:\(\sqrt{x-1}+2=\sqrt{2 x+6}\)
- Resposta
-
\(x=5\)
Resolver:\(\sqrt{x}+2=\sqrt{3 x+4}\)
- Resposta
-
\(x=0 x=4\)
Use radicais em aplicações
Conforme você avança nos cursos universitários, você encontrará fórmulas que incluem radicais em muitas disciplinas. Modificaremos um pouco nossa estratégia de resolução de problemas para aplicações de geometria para nos dar um plano para resolver aplicativos com fórmulas de qualquer disciplina.
Use uma estratégia de solução de problemas para aplicativos com fórmulas
- Leia o problema e certifique-se de que todas as palavras e ideias sejam compreendidas. Quando apropriado, desenhe uma figura e identifique-a com as informações fornecidas.
- Identifique o que estamos procurando.
- Nomeie o que estamos procurando escolhendo uma variável para representá-la.
- Traduza em uma equação escrevendo a fórmula ou modelo apropriado para a situação. Substitua as informações fornecidas.
- Resolva a equação usando boas técnicas de álgebra.
- Verifique a resposta do problema e verifique se faz sentido.
- Responda à pergunta com uma frase completa.
Uma aplicação de radicais tem a ver com o efeito da gravidade na queda de objetos. A fórmula nos permite determinar quanto tempo um objeto caído levará para atingir o solo.
Definição\(\PageIndex{2}\)
Objetos caindo
Na Terra, se um objeto cair de uma altura de\(h\) pés, o tempo em segundos necessário para chegar ao solo é encontrado usando a fórmula
\(t=\frac{\sqrt{h}}{4}\)
Por exemplo, se um objeto cair de uma altura de\(64\) pés, podemos encontrar o tempo necessário para chegar ao solo\(h=64\) substituindo-o pela fórmula.
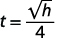 |
|
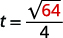 |
|
| Pegue a raiz quadrada de\(64\). | 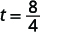 |
| Simplifique a fração. | 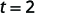 |
Levaria\(2\) segundos para que um objeto caído de uma altura de\(64\) pés alcançasse o solo.
Marissa deixou cair os óculos de sol de uma ponte a\(400\) poucos metros acima de um rio. Use a fórmula\(t=\frac{\sqrt{h}}{4}\) para descobrir quantos segundos foram necessários para os óculos de sol chegarem ao rio.
Solução:
| Etapa 1: Leia o problema. | |
| Etapa 2: Identifique o que estamos procurando. | O tempo necessário para os óculos de sol chegarem ao rio. |
| Etapa 3: nomeie o que estamos procurando. | Deixe (t=\) hora. |
| Etapa 4: traduza em uma equação escrevendo a fórmula apropriada. Substitua as informações fornecidas. | 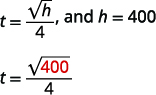 |
| Etapa 5: Resolva a equação. |  |
 |
|
| Etapa 6: verifique a resposta do problema e verifique se faz sentido. | 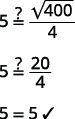 |
| Os\(5\) segundos parecem um período de tempo razoável? | Sim. |
| Etapa 7: Responda à equação. | Levará\(5\) alguns segundos para que os óculos de sol cheguem ao rio. |
Um helicóptero deixou cair um pacote de resgate de uma altura de\(1,296\) pés. Use a fórmula\(t=\frac{\sqrt{h}}{4}\) para descobrir quantos segundos o pacote levou para chegar ao solo.
- Resposta
-
\(9\)segundos
Um lavador de janelas derrubou um rodo de uma plataforma,\(196\) pés acima da calçada. Use a fórmula\(t=\frac{\sqrt{h}}{4}\) para descobrir quantos segundos o rodo levou para chegar à calçada.
- Resposta
-
\(3.5\)segundos
Policiais que investigam acidentes de carro medem o comprimento das marcas de derrapagem na calçada. Em seguida, eles usam raízes quadradas para determinar a velocidade, em milhas por hora, que um carro estava andando antes de acionar os freios.
Definição\(\PageIndex{3}\)
Marcas de derrapagem e velocidade de um carro
Se o comprimento das marcas de derrapagem for\(d\) pés, a velocidade\(s\),, do carro antes da aplicação dos freios pode ser encontrada usando a fórmula
\(s=\sqrt{24 d}\)
Depois de um acidente de carro, as marcas de derrapagem de um carro mediram\(190\) pés. Use a fórmula\(s=\sqrt{24d}\) para determinar a velocidade do carro antes que os freios sejam aplicados. Arredonde sua resposta para o décimo mais próximo.
Solução:
| Etapa 1: Leia o problema. | |
| Etapa 2: Identifique o que estamos procurando. | A velocidade de um carro. |
| Etapa 3: nomeie o que estamos procurando. | Deixe\(s=\) a velocidade. |
| Etapa 4: traduza em uma equação escrevendo a fórmula apropriada. Substitua as informações fornecidas. | 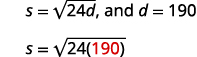 |
| Etapa 5: Resolva a equação. | 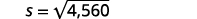 |
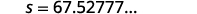 |
|
| Arredondar para a\(1\) casa decimal. |  |
 |
|
| A velocidade do carro antes da aplicação dos freios era de\(67.5\) milhas por hora. |
Um investigador de acidentes mediu as marcas de derrapagem do carro. O comprimento das marcas de derrapagem era de\(76\) pés. Use a fórmula\(s=\sqrt{24d}\) para determinar a velocidade do carro antes que os freios sejam aplicados. Arredonde sua resposta para o décimo mais próximo.
- Resposta
-
\(42.7\)pés
As marcas de derrapagem de um veículo envolvido em um acidente tinham\(122\) pés de comprimento. Use a fórmula\(s=\sqrt{24d}\) para determinar a velocidade do veículo antes que os freios sejam aplicados. Arredonde sua resposta para o décimo mais próximo.
- Resposta
-
\(54.1\)pés
Acesse esses recursos on-line para obter instruções e práticas adicionais na resolução de equações radicais.
- Resolvendo uma equação envolvendo um único radical
- Resolvendo equações com radicais e expoentes racionais
- Resolvendo equações radicais
- Resolva equações radicais
- Aplicação de equações radicais
Conceitos chave
- Quadrados binomiais
\(\begin{array}{l}{(a+b)^{2}=a^{2}+2 a b+b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}\) - Resolva uma equação radical
- Isole um dos termos radicais em um lado da equação.
- Eleve os dois lados da equação até a potência do índice.
- Existem mais radicais?
Se sim, repita a Etapa 1 e a Etapa 2 novamente.
Se não, resolva a nova equação. - Verifique a resposta na equação original.
- Estratégia de resolução de problemas para aplicativos com fórmulas
- Leia o problema e certifique-se de que todas as palavras e ideias sejam compreendidas. Quando apropriado, desenhe uma figura e identifique-a com as informações fornecidas.
- Identifique o que estamos procurando.
- Nomeie o que estamos procurando escolhendo uma variável para representá-la.
- Traduza em uma equação escrevendo a fórmula ou modelo apropriado para a situação. Substitua as informações fornecidas.
- Resolva a equação usando boas técnicas de álgebra.
- Verifique a resposta do problema e verifique se faz sentido.
- Responda à pergunta com uma frase completa.
- Objetos caindo
- Na Terra, se um objeto cair de uma altura de\(h\) pés, o tempo em segundos necessário para chegar ao solo é encontrado usando a fórmula\(t=\frac{\sqrt{h}}{4}\).
- Marcas de derrapagem e velocidade de um carro
- Se o comprimento das marcas de derrapagem for em\(d\) pés, a velocidade\(s\),, do carro antes da aplicação dos freios pode ser encontrada usando a fórmula\(s=\sqrt{24d}\).
Glossário
- equação radical
- Uma equação na qual uma variável está no radicando de uma expressão radical é chamada de equação radical.


