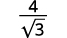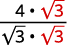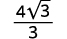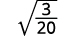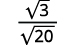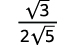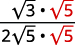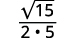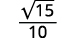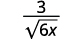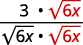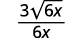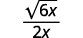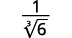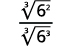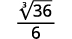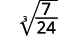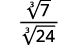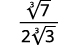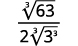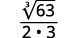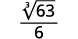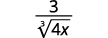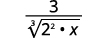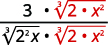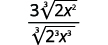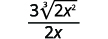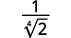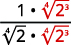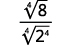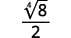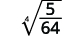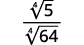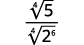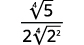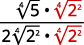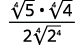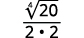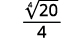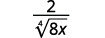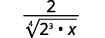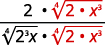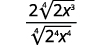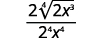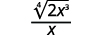8.6: Divida expressões radicais
- Page ID
- 183450
Ao final desta seção, você poderá:
- Divida expressões radicais
- Racionalizar um denominador de um termo
- Racionalizar um denominador de dois termos
Antes de começar, faça este teste de prontidão.
- Simplifique:\(\dfrac{30}{48}\).
Se você perdeu esse problema, revise o Exemplo 1.24. - Simplifique:\(x^{2}⋅x^{4}\).
Se você perdeu esse problema, consulte o Exemplo 5.12. - Multiplique:\((7+3x)(7−3x)\).
Se você perdeu esse problema, consulte o Exemplo 5.32.
Divida expressões radicais
Usamos a propriedade quociente de expressões radicais para simplificar as raízes das frações. Precisaremos usar essa propriedade “ao contrário” para simplificar uma fração com radicais. Fornecemos novamente a propriedade quociente de expressões radicais para facilitar a referência. Lembre-se de que assumimos que todas as variáveis são maiores ou iguais a zero, de modo que nenhuma barra de valor absoluto é necessária.
Definição\(\PageIndex{1}\): Quotient Property of Radical Expressions
Se\(\sqrt[n]{a}\) e\(\sqrt[n]{b}\) forem números reais,\(b≠0\), e para qualquer número inteiro,\(n≥2\) então,
\(\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}} \quad \text { and } \quad \dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\)
Usaremos a propriedade quociente de expressões radicais quando a fração com a qual começamos for o quociente de dois radicais, e nenhum dos radicandos for uma potência perfeita do índice. Quando escrevemos a fração em um único radical, podemos encontrar fatores comuns no numerador e no denominador.
Simplifique:
- \(\dfrac{\sqrt{72 x^{3}}}{\sqrt{162 x}}\)
- \(\dfrac{\sqrt[3]{32 x^{2}}}{\sqrt[3]{4 x^{5}}}\)
Solução:
uma.
\(\dfrac{\sqrt{72 x^{3}}}{\sqrt{162 x}}\)
Reescreva usando a propriedade do quociente,
\(\sqrt{\dfrac{72 x^{3}}{162 x}}\)
Remova os fatores comuns.
\(\sqrt{\dfrac{\cancel{18} \cdot 4 \cdot x^{2} \cdot \cancel{x}}{\cancel{18} \cdot 9 \cdot \cancel{x}}}\)
Simplifique.
\(\sqrt{\dfrac{4 x^{2}}{9}}\)
Simplifique o radical.
\(\dfrac{2 x}{3}\)
b.
\(\dfrac{\sqrt[3]{32 x^{2}}}{\sqrt[3]{4 x^{5}}}\)
Reescreva usando a propriedade do quociente,\(\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\).
\(\sqrt[3]{\dfrac{32 x^{2}}{4 x^{5}}}\)
Simplifique a fração abaixo do radical.
\(\sqrt[3]{\dfrac{8}{x^{3}}}\)
Simplifique o radical.
\(\dfrac{2}{x}\)
Simplifique:
- \(\dfrac{\sqrt{50 s^{3}}}{\sqrt{128 s}}\)
- \(\dfrac{\sqrt[3]{56 a}}{\sqrt[3]{7 a^{4}}}\)
- Resposta
-
- \(\dfrac{5s}{8}\)
- \(\dfrac{2}{a}\)
Simplifique:
- \(\dfrac{\sqrt{75 q^{5}}}{\sqrt{108 q}}\)
- \(\dfrac{\sqrt[3]{72 b^{2}}}{\sqrt[3]{9 b^{5}}}\)
- Resposta
-
- \(\dfrac{5 q^{2}}{6}\)
- \(\dfrac{2}{b}\)
Simplifique:
- \(\dfrac{\sqrt{147 a b^{8}}}{\sqrt{3 a^{3} b^{4}}}\)
- \(\dfrac{\sqrt[3]{-250 m n^{-2}}}{\sqrt[3]{2 m^{-2} n^{4}}}\)
Solução:
uma.
\(\dfrac{\sqrt{147 a b^{8}}}{\sqrt{3 a^{3} b^{4}}}\)
Reescreva usando a propriedade do quociente.
\(\sqrt{\dfrac{147 a b^{8}}{3 a^{3} b^{4}}}\)
Remova os fatores comuns na fração.
\(\sqrt{\dfrac{49 b^{4}}{a^{2}}}\)
Simplifique o radical.
\(\dfrac{7 b^{2}}{a}\)
b.
\(\dfrac{\sqrt[3]{-250 m n^{-2}}}{\sqrt[3]{2 m^{-2} n^{4}}}\)
Reescreva usando a propriedade do quociente.
\(\sqrt[3]{\dfrac{-250 m n^{-2}}{2 m^{-2} n^{4}}}\)
Simplifique a fração abaixo do radical.
\(\sqrt[3]{\dfrac{-125 m^{3}}{n^{6}}}\)
Simplifique o radical.
\(-\dfrac{5 m}{n^{2}}\)
Simplifique:
- \(\dfrac{\sqrt{162 x^{10} y^{2}}}{\sqrt{2 x^{6} y^{6}}}\)
- \(\dfrac{\sqrt[3]{-128 x^{2} y^{-1}}}{\sqrt[3]{2 x^{-1} y^{2}}}\)
- Resposta
-
- \(\dfrac{9 x^{2}}{y^{2}}\)
- \(\dfrac{-4 x}{y}\)
Simplifique:
- \(\dfrac{\sqrt{300 m^{3} n^{7}}}{\sqrt{3 m^{5} n}}\)
- \(\dfrac{\sqrt[3]{-81 p q^{-1}}}{\sqrt[3]{3 p^{-2} q^{5}}}\)
- Resposta
-
- \(\dfrac{10 n^{3}}{m}\)
- \(\dfrac{-3 p}{q^{2}}\)
Simplifique:\(\dfrac{\sqrt{54 x^{5} y^{3}}}{\sqrt{3 x^{2} y}}\)
Solução:
\(\dfrac{\sqrt{54 x^{5} y^{3}}}{\sqrt{3 x^{2} y}}\)
Reescreva usando a propriedade do quociente.
\(\sqrt{\dfrac{54 x^{5} y^{3}}{3 x^{2} y}}\)
Remova os fatores comuns na fração.
\(\sqrt{18 x^{3} y^{2}}\)
Reescreva o radicando como um produto usando o maior fator quadrado perfeito.
\(\sqrt{9 x^{2} y^{2} \cdot 2 x}\)
Reescreva o radical como produto de dois radicais.
\(\sqrt{9 x^{2} y^{2}} \cdot \sqrt{2 x}\)
Simplifique.
\(3 x y \sqrt{2 x}\)
Simplifique:\(\dfrac{\sqrt{64 x^{4} y^{5}}}{\sqrt{2 x y^{3}}}\)
- Resposta
-
\(4 x y \sqrt{2 x}\)
Simplifique:\(\dfrac{\sqrt{96 a^{5} b^{4}}}{\sqrt{2 a^{3} b}}\)
- Resposta
-
\(4 a b \sqrt{3 b}\)
Racionalizar um denominador de um termo
Antes de a calculadora se tornar uma ferramenta da vida cotidiana, aproximar o valor de uma fração com um radical no denominador era um processo muito complicado!
Por esse motivo, um processo chamado racionalização do denominador foi desenvolvido. Uma fração com um radical no denominador é convertida em uma fração equivalente cujo denominador é um número inteiro. As raízes quadradas de números que não são quadrados perfeitos são números irracionais. Quando racionalizamos o denominador, escrevemos uma fração equivalente com um número racional no denominador. Esse processo ainda é usado hoje e também é útil em outras áreas da matemática.
Definição\(\PageIndex{2}\): Rationalizing the Denominator
Racionalizar o denominador é o processo de conversão de uma fração com um radical no denominador em uma fração equivalente cujo denominador é um número inteiro.
Embora tenhamos calculadoras disponíveis em quase todos os lugares, uma fração com um radical no denominador ainda precisa ser racionalizada. Não é considerado simplificado se o denominador contiver um radical.
Da mesma forma, uma expressão radical não é considerada simplificada se o radicando contiver uma fração.
Expressões radical simplificadas
Uma expressão radical é considerada simplificada se houver
- nenhum fator no radical tem poderes perfeitos do índice
- sem frações no radicando
- nenhum radical no denominador de uma fração
Para racionalizar um denominador com raiz quadrada, usamos a propriedade que\((\sqrt{a})^{2}=a\). Se quadrarmos uma raiz quadrada irracional, obteremos um número racional.
Usaremos essa propriedade para racionalizar o denominador no próximo exemplo.
Simplifique:
- \(\dfrac{4}{\sqrt{3}}\)
- \(\sqrt{\dfrac{3}{20}}\)
- \(\dfrac{3}{\sqrt{6 x}}\)
Solução:
Para racionalizar um denominador com um termo, podemos multiplicar uma raiz quadrada por si mesma. Para manter a fração equivalente, multiplicamos o numerador e o denominador pelo mesmo fator.
uma.
|
|
|
| Multiplique o numerador e o denominador por\(\sqrt{3}\). |
|
| Simplifique. |
|
b. Sempre simplificamos primeiro o radical no denominador, antes de racionalizá-lo. Dessa forma, os números permanecem menores e mais fáceis de trabalhar.
|
|
|
| A fração não é um quadrado perfeito, então reescreva usando a propriedade do quociente. |
|
| Simplifique o denominador. |
|
| Multiplique o numerador e o denominador por\(\sqrt{5}\). |
|
| Simplifique. |
|
| Simplifique. |
|
c.
|
|
|
| Multiplique o numerador e o denominador por\(\sqrt{6x}\). |
|
| Simplifique. |
|
| Simplifique. |
|
Simplifique:
- \(\dfrac{5}{\sqrt{3}}\)
- \(\sqrt{\dfrac{3}{32}}\)
- \(\dfrac{2}{\sqrt{2 x}}\)
- Resposta
-
- \(\dfrac{5 \sqrt{3}}{3}\)
- \(\dfrac{\sqrt{6}}{8}\)
- \(\dfrac{\sqrt{2 x}}{x}\)
Simplifique:
- \(\dfrac{6}{\sqrt{5}}\)
- \(\sqrt{\dfrac{7}{18}}\)
- \(\dfrac{5}{\sqrt{5 x}}\)
- Resposta
-
- \(\dfrac{6 \sqrt{5}}{5}\)
- \(\dfrac{\sqrt{14}}{6}\)
- \(\dfrac{\sqrt{5 x}}{x}\)
Quando racionalizamos uma raiz quadrada, multiplicamos o numerador e o denominador por uma raiz quadrada que nos daria um quadrado perfeito abaixo do radical no denominador. Quando pegamos a raiz quadrada, o denominador não tinha mais um radical.
Seguiremos um processo semelhante para racionalizar raízes superiores. Para racionalizar um denominador com um radical de índice mais alto, multiplicamos o numerador e o denominador por um radical que nos daria um radicando que é a potência perfeita do índice. Quando simplificarmos o novo radical, o denominador não terá mais um radical.
Por exemplo,
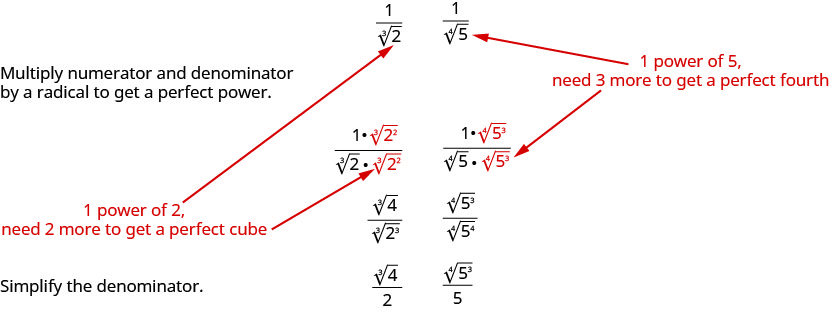
Usaremos essa técnica nos próximos exemplos.
Simplifique:
- \(\dfrac{1}{\sqrt[3]{6}}\)
- \(\sqrt[3]{\dfrac{7}{24}}\)
- \(\dfrac{3}{\sqrt[3]{4 x}}\)
Solução:
Para racionalizar um denominador com uma raiz cúbica, podemos multiplicar por uma raiz cúbica que nos dará um cubo perfeito no radicando no denominador. Para manter a fração equivalente, multiplicamos o numerador e o denominador pelo mesmo fator.
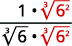
uma.
|
|
|
| O radical no denominador tem um fator de\(6\). Multiplique o numerador e o denominador por\(\sqrt[3]{6^{2}}\), o que nos dá\(2\) mais fatores de\(6\). |
|
| Multiplique. Observe que o radicando no denominador tem\(3\) poderes de\(6\). |
|
| Simplifique a raiz cúbica no denominador. |
|
b. Sempre simplificamos primeiro o radical no denominador, antes de racionalizá-lo. Dessa forma, os números permanecem menores e mais fáceis de trabalhar.
|
|
|
| A fração não é um cubo perfeito, então reescreva usando a propriedade do quociente. |
|
| Simplifique o denominador. |
|
| Multiplique o numerador e o denominador por\(\sqrt[3]{3^{2}}\). Isso nos dará\(3\) fatores de\(3\). |
|
| Simplifique. |
|
| Lembre-se,\(\sqrt[3]{3^{3}}=3\). |
|
| Simplifique. |
|
c.
|
|
|
| Reescreva o radicando para mostrar os fatores. |
|
| Multiplique o numerador e o denominador por\(\sqrt[3]{2 \cdot x^{2}}\). Isso nos dará\(3\) fatores\(2\) e\(3\) fatores de\(x\). |
|
| Simplifique. |
|
| Simplifique o radical no denominador. |
|
Simplifique:
- \(\dfrac{1}{\sqrt[3]{7}}\)
- \(\sqrt[3]{\dfrac{5}{12}}\)
- \(\dfrac{5}{\sqrt[3]{9 y}}\)
- Resposta
-
- \(\dfrac{\sqrt[3]{49}}{7}\)
- \(\dfrac{\sqrt[3]{90}}{6}\)
- \(\dfrac{5 \sqrt[3]{3 y^{2}}}{3 y}\)
Simplifique:
- \(\dfrac{1}{\sqrt[3]{2}}\)
- \(\sqrt[3]{\dfrac{3}{20}}\)
- \(\dfrac{2}{\sqrt[3]{25 n}}\)
- Resposta
-
- \(\dfrac{\sqrt[3]{4}}{2}\)
- \(\dfrac{\sqrt[3]{150}}{10}\)
- \(\dfrac{2 \sqrt[3]{5 n^{2}}}{5 n}\)
Simplifique:
- \(\dfrac{1}{\sqrt[4]{2}}\)
- \(\sqrt[4]{\dfrac{5}{64}}\)
- \(\dfrac{2}{\sqrt[4]{8 x}}\)
Solução:
Para racionalizar um denominador com uma quarta raiz, podemos multiplicar por uma quarta raiz que nos dará uma quarta potência perfeita no radicando no denominador. Para manter a fração equivalente, multiplicamos o numerador e o denominador pelo mesmo fator.
uma.
|
|
|
| O radical no denominador tem um fator de\(2\). Multiplique o numerador e o denominador por\(\sqrt[4]{2^{3}}\), o que nos dá\(3\) mais fatores de\(2\). |
|
| Multiplique. Observe que o radicando no denominador tem\(4\) poderes de\(2\). |
|
| Simplifique a quarta raiz no denominador. |
|
b. Sempre simplificamos primeiro o radical no denominador, antes de racionalizá-lo. Dessa forma, os números permanecem menores e mais fáceis de trabalhar.
|
|
|
| A fração não é uma quarta potência perfeita, então reescreva usando a propriedade do quociente. |
|
| Reescreva o radicando no denominador para mostrar os fatores. |
|
| Simplifique o denominador. |
|
| Multiplique o numerador e o denominador por\(\sqrt[4]{2^{2}}\). Isso nos dará\(4\) fatores de\(2\). |
|
| Simplifique. |
|
| Lembre-se,\(\sqrt[4]{2^{4}}=2\). |
|
| Simplifique. |
|
c.
|
|
|
| Reescreva o radicando para mostrar os fatores. |
|
| Multiplique o numerador e o denominador por\(\sqrt[4]{2 \cdot x^{3}}\). Isso nos dará\(4\) fatores\(2\) e\(4\) fatores de\(x\). |
|
| Simplifique. |
|
| Simplifique o radical no denominador. |
|
| Simplifique a fração. |
|
Simplifique:
- \(\dfrac{1}{\sqrt[4]{3}}\)
- \(\sqrt[4]{\dfrac{3}{64}}\)
- \(\dfrac{3}{\sqrt[4]{125 x}}\)
- Resposta
-
- \(\dfrac{\sqrt[4]{27}}{3}\)
- \(\dfrac{\sqrt[4]{12}}{4}\)
- \(\dfrac{3 \sqrt[4]{5 x^{3}}}{5 x}\)
Simplifique:
- \(\dfrac{1}{\sqrt[4]{5}}\)
- \(\sqrt[4]{\dfrac{7}{128}}\)
- \(\dfrac{4}{\sqrt[4]{4 x}}\)
- Resposta
-
- \(\dfrac{\sqrt[4]{125}}{5}\)
- \(\dfrac{\sqrt[4]{224}}{8}\)
- \(\dfrac{\sqrt[4]{64 x^{3}}}{x}\)
Racionalizar um denominador de dois termos
Quando o denominador de uma fração é uma soma ou diferença com raízes quadradas, usamos o Padrão Produto de Conjugados para racionalizar o denominador.
\(\begin{array}{c c}{(a-b)(a+b)} & {(2-\sqrt{5})(2+\sqrt{5})} \\ {a^{2}-b^{2}} &{ 2^{2}-(\sqrt{5})^{2}} \\ {}&{4-5} \\ {}&{-1}\end{array}\)
Quando multiplicamos um binômio que inclui uma raiz quadrada por seu conjugado, o produto não tem raízes quadradas.
Simplifique:\(\dfrac{5}{2-\sqrt{3}}\)
Solução:
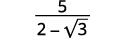 |
|
| Multiplique o numerador e o denominador pelo conjugado do denominador. | 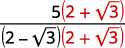 |
| Multiplique os conjugados no denominador. | 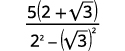 |
| Simplifique o denominador. | 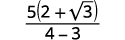 |
| Simplifique o denominador. | 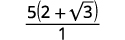 |
| Simplifique. | 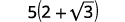 |
Simplifique:\(\dfrac{3}{1-\sqrt{5}}\).
- Resposta
-
\(-\dfrac{3(1+\sqrt{5})}{4}\)
Simplifique:\(\dfrac{2}{4-\sqrt{6}}\).
- Resposta
-
\(\dfrac{4+\sqrt{6}}{5}\)
Observe que não distribuímos o\(5\) na resposta do último exemplo. Ao deixar o resultado fatorado, podemos ver se há algum fator que possa ser comum tanto ao numerador quanto ao denominador.
Simplifique:\(\dfrac{\sqrt{3}}{\sqrt{u}-\sqrt{6}}\).
Solução:
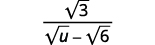 |
|
| Multiplique o numerador e o denominador pelo conjugado do denominador. | 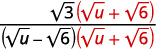 |
| Multiplique os conjugados no denominador. | 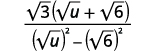 |
| Simplifique o denominador. | 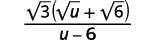 |
Simplifique:\(\dfrac{\sqrt{5}}{\sqrt{x}+\sqrt{2}}\).
- Resposta
-
\(\dfrac{\sqrt{5}(\sqrt{x}-\sqrt{2})}{x-2}\)
Simplifique:\(\dfrac{\sqrt{10}}{\sqrt{y}-\sqrt{3}}\)
- Resposta
-
\(\dfrac{\sqrt{10}(\sqrt{y}+\sqrt{3})}{y-3}\)
Tenha cuidado com os sinais ao multiplicar. O numerador e o denominador parecem muito semelhantes quando você multiplica pelo conjugado.
Simplifique:\(\dfrac{\sqrt{x}+\sqrt{7}}{\sqrt{x}-\sqrt{7}}\).
Solução:
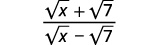 |
|
| Multiplique o numerador e o denominador pelo conjugado do denominador. |  |
| Multiplique os conjugados no denominador. | 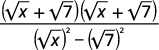 |
| Simplifique o denominador. | 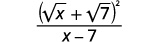 |
Não colocamos o numerador ao quadrado. Deixando-o na forma fatorada, podemos ver que não há fatores comuns a serem removidos do numerador e do denominador.
Simplifique:\(\dfrac{\sqrt{p}+\sqrt{2}}{\sqrt{p}-\sqrt{2}}\).
- Resposta
-
\(\dfrac{(\sqrt{p}+\sqrt{2})^{2}}{p-2}\)
Simplifique:\(\dfrac{\sqrt{q}-\sqrt{10}}{\sqrt{q}+\sqrt{10}}\)
- Resposta
-
\(\dfrac{(\sqrt{q}-\sqrt{10})^{2}}{q-10}\)
Conceitos-chave
- Propriedade quociente de expressões radicais
- Se\(\sqrt[n]{a}\) e\(\sqrt[n]{b}\) forem números reais,\(b≠0\), e para qualquer número inteiro,\(n≥2\) então,\(\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}\) e\(\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\dfrac{a}{b}}\)
- Expressões radical simplificadas
- Uma expressão radical é considerada simplificada se houver:
- nenhum fator no radicando que tenha poderes perfeitos do índice
- sem frações no radicando
- nenhum radical no denominador de uma fração
- Uma expressão radical é considerada simplificada se houver:
Glossário
- racionalizando o denominador
- Racionalizar o denominador é o processo de conversão de uma fração com um radical no denominador em uma fração equivalente cujo denominador é um número inteiro.