6.6: Equações polinomiais
- Page ID
- 183320
Ao final desta seção, você poderá:
- Use a propriedade Zero Product
- Resolva equações quadráticas por fatoração
- Resolva equações com funções polinomiais
- Resolva aplicações modeladas por equações polinomiais
Antes de começar, faça este teste de prontidão.
Passamos um tempo considerável aprendendo como fatorar polinômios. Agora, examinaremos as equações polinomiais e as resolveremos usando fatoração, se possível.
Uma equação polinomial é uma equação que contém uma expressão polinomial. O grau da equação polinomial é o grau do polinômio.
Uma equação polinomial é uma equação que contém uma expressão polinomial.
O grau da equação polinomial é o grau do polinômio.
Já resolvemos equações polinomiais de grau um. As equações polinomiais de grau um são equações lineares que têm a forma\(ax+b=c\).
Agora vamos resolver equações polinomiais de grau dois. Uma equação polinomial de grau dois é chamada de equação quadrática. Listados abaixo estão alguns exemplos de equações quadráticas:
\[x^2+5x+6=0 \qquad 3y^2+4y=10 \qquad 64u^2−81=0 \qquad n(n+1)=42 \nonumber\]
A última equação não parece ter a variável ao quadrado, mas quando simplificarmos a expressão à esquerda, obteremos\(n^2+n\).
A forma geral de uma equação quadrática é\(ax^2+bx+c=0\), com\(a\neq 0\). (Se\(a=0\), então\(0·x^2=0\) e ficamos sem termo quadrático.)
Uma equação da forma\(ax^2+bx+c=0\) é chamada de equação quadrática.
\[a,b,\text{ and }c\text{ are real numbers and }a\neq 0\nonumber\]
Para resolver equações quadráticas, precisamos de métodos diferentes dos que usamos na solução de equações lineares. Examinaremos um método aqui e, em seguida, vários outros em um capítulo posterior.
Use a propriedade Zero Product
Primeiro, resolveremos algumas equações quadráticas usando a Propriedade do Produto Zero. A Propriedade do Produto Zero diz que, se o produto de duas quantidades for zero, pelo menos uma das quantidades será zero. A única maneira de obter um produto igual a zero é multiplicar pelo próprio zero.
Se\(a·b=0\), então, um\(a=0\)\(b=0\) ou ambos.
Agora usaremos a Propriedade do Produto Zero para resolver uma equação quadrática.
Resolver:\((5n−2)(6n−1)=0\).
- Responda
-



Resolver:\((3m−2)(2m+1)=0\).
- Responda
-
\(m=\frac{2}{3},\space m=−\frac{1}{2}\)
Resolver:\((4p+3)(4p−3)=0\).
- Responda
-
\(p=−\frac{3}{4},\space p=\frac{3}{4}\)
- Defina cada fator igual a zero.
- Resolva as equações lineares.
- Confira.
Resolva equações quadráticas por fatoração
A Propriedade do Produto Zero funciona muito bem para resolver equações quadráticas. A equação quadrática deve ser fatorada, com zero isolado em um lado. Portanto, certifique-se de começar com a equação quadrática na forma padrão,\(ax^2+bx+c=0\). Em seguida, fatoramos a expressão à esquerda.
Resolver:\(2y^2=13y+45\).
- Responda
-

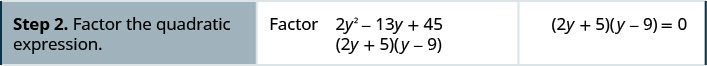


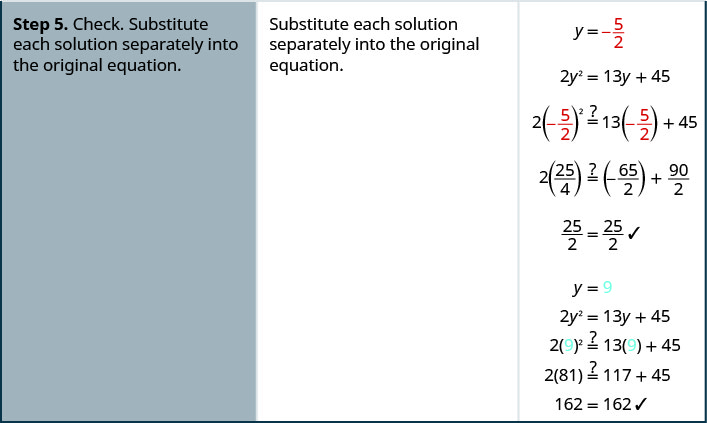
Resolver:\(3c^2=10c−8\).
- Responda
-
\(c=2,\space c=\frac{4}{3}\)
Resolver:\(2d^2−5d=3\).
- Responda
-
\(d=3,\space d=−12\)
- Escreva a equação quadrática na forma padrão,\(ax^2+bx+c=0\).
- Considere a expressão quadrática.
- Use a propriedade Zero Product.
- Resolva as equações lineares.
- Confira. Substitua cada solução separadamente na equação original.
Antes de fatorarmos, devemos garantir que a equação quadrática esteja na forma padrão.
Resolver equações quadráticas por fatoração fará uso de todas as técnicas de fatoração que você aprendeu neste capítulo! Você reconhece o padrão especial do produto no próximo exemplo?
Resolver:\(169q^2=49\).
- Responda
-
\(\begin{array} {ll} &169x^2=49 \\ \text{Write the quadratic equation in standard form.} &169x^2−49=0 \\ \text{Factor. It is a difference of squares.} &(13x−7)(13x+7)=0 \\ \text{Use the Zero Product Property to set each factor to }0. & \\ \text{Solve each equation.} &\begin{array} {ll} 13x−7=0 &13x+7=0 \\ 13x=7 &13x=−7 \\ x=\frac{7}{13} &x=−\frac{7}{13} \end{array} \end{array}\)
Confira:
Deixamos o cheque para você.
Resolver:\(25p^2=49\).
- Responda
-
\(p=\frac{7}{5},p=−\frac{7}{5}\)
Resolver:\(36x^2=121\).
- Responda
-
\(x=\frac{11}{6},x=−\frac{11}{6}\)
No próximo exemplo, o lado esquerdo da equação é fatorado, mas o lado direito não é zero. Para usar a Propriedade do Produto Zero, um lado da equação deve ser zero. Multiplicaremos os fatores e, em seguida, escreveremos a equação na forma padrão.
Resolver:\((3x−8)(x−1)=3x\).
- Responda
-
\(\begin{array} {ll} &(3x−8)(x−1)=3x \\ \text{Multiply the binomials.} &3x^2−11x+8=3x \\ \text{Write the quadratic equation in standard form.} &3x^2−14x+8=0 \\ \text{Factor the trinomial.} &(3x−2)(x−4)=0 \\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} \end{array} &\begin{array} {ll} 3x−2=0 &x−4=0 \\ 3x=2 &x=4 \\ x=\frac{2}{3} & \end{array} \\ \text{Check your answers.} &\text{The check is left to you.} \end{array}\)
Resolver:\((2m+1)(m+3)=12m\).
- Responda
-
\(m=1,\space m=\frac{3}{2}\)
Resolver:\((k+1)(k−1)=8\).
- Responda
-
\(k=3,\space k=−3\)
No próximo exemplo, quando fatorarmos a equação quadrática, obteremos três fatores. No entanto, o primeiro fator é uma constante. Sabemos que esse fator não pode ser igual a 0.
Resolver:\(3x^2=12x+63\).
- Responda
-
\(\begin{array} {ll} &3x^2=12x+63 \\ \text{Write the quadratic equation in standard form.} &3x^2−12x−63=0 \\ \text{Factor the greatest common factor first.} &3(x^2−4x−21)=0 \\ \text{Factor the trinomial.} &3(x−7)(x+3)=0 \\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} \end{array} &\begin{array} {lll} 3\neq 0 &x−7=0 &x+3=0 \\ 3\neq 0 &x=7 &x=−3 \end{array} \\ \text{Check your answers.} &\text{The check is left to you.} \end{array}\)
Resolver:\(18a^2−30=−33a\).
- Responda
-
\(a=−\frac{5}{2},a=\frac{2}{3}\)
Resolver:\(123b=−6−60b^2\)
- Responda
-
\(b=−2,\space b=−\frac{1}{20}\)
A Propriedade do Produto Zero também se aplica ao produto de três ou mais fatores. Se o produto for zero, pelo menos um dos fatores deve ser zero. Podemos resolver algumas equações de grau maior que dois usando a Propriedade do Produto Zero, assim como resolvemos equações quadráticas.
Resolver:\(9m^3+100m=60m^2\)
- Responda
-
\(\begin{array} {ll} & 9m^3+100m=60m^2 \\ \text{Bring all the terms to one side so that the other side is zero.} &9m^3−60m^2+100m=0 \\ \text{Factor the greatest common factor first.} &m(9m^2−60m+100)=0 \\ \text{Factor the trinomial.} &m(3m−10)^2=0 \end{array}\\ \begin{array} {l} \text{Use the Zero Product Property to set each factor to 0.} \\ \text{Solve each equation.} &\begin{array} {lll} m=0 &3m−10=0 &{}\\ m=0 &m=\frac{10}{3} & {} \end{array}\\ \text{Check your answers.} &\text{The check is left to you.} \end{array}\)
Resolver:\(8x^3=24x^2−18x\).
- Responda
-
\(x=0,\space x=\frac{3}{2}\)
Resolver:\(16y^2=32y^3+2y\).
- Responda
-
\(y=0,\space y=14\)
Resolva equações com funções polinomiais
À medida que nosso estudo das funções polinomiais continua, muitas vezes será importante saber quando a função terá um determinado valor ou quais pontos estão no gráfico da função. Nosso trabalho com a Zero Product Property nos ajudará a encontrar essas respostas.
Para a função\(f(x)=x^2+2x−2\),
ⓐ encontre\(x\) quando\(f(x)=6\)
ⓑ encontre dois pontos que estão no gráfico da função.
- Responda
-
ⓐ
\(\begin{array} {ll} &f(x)=x^2+2x−2 \\ \text{Substitute }6\text{ for }f(x). &6=x^2+2x−2 \\ \text{Put the quadratic in standard form.} &x^2+2x−8=0 \\ \text{Factor the trinomial.} &(x+4)(x−2)=0 \\ \begin{array} {l} \text{Use the zero product property.} \\ \text{Solve.} \end{array} &\begin{array} {lll} x+4=0 &\text{or} &x−2=0 \\ x=−4 &\text{or} &x=2 \end{array} \\ \text{Check:} & \\ & \\ & \\ & \\ & \\ & \\ & \\ & \\ & \\ \begin{array} {lll} \quad &\hspace{3mm} f(x)=x^2+2x−2 &f(x)=x^2+2x−2 \\ \quad &f(−4)=(−4)^2+2(−4)−2 &f(2)=2^2+2·2−2 \\ \quad &f(−4)=16−8−2 &f(2)=4+4−2 \\ \quad &f(−4)=6\checkmark &f(2)=6\checkmark \end{array} & \end{array} \)
ⓑ Desde\(f(−4)=6\) e\(f(2)=6\), os pontos\((−4,6)\)\((2,6)\) estão no gráfico da função.
Para a função\(f(x)=x^2−2x−8\),
ⓐ encontre\(x\) quando\(f(x)=7\)
ⓑ Encontre dois pontos que estão no gráfico da função.
- Responda
-
ⓐ\(x=−3\) ou\(x=5\)
ⓑ\((−3,7)\space (5,7)\)
Para a função\(f(x)=x^2−8x+3\),
ⓐ encontre\(x\) quando\(f(x)=−4\)
ⓑ Encontre dois pontos que estão no gráfico da função.
- Responda
-
ⓐ\(x=1\) ou\(x=7\)
ⓑ\((1,−4)\space (7,−4)\)
A Propriedade do Produto Zero também nos ajuda a determinar onde a função é zero. Um valor de\(x\) onde a função está\(0\) é chamado de zero da função.
Para qualquer função\(f\), if\(f(x)=0\), então\(x\) é um zero da função.
Quando\(f(x)=0\), o ponto\((x,0)\) é um ponto no gráfico. Este ponto é uma interceptação\(x\) - do gráfico. Muitas vezes, é importante saber onde o gráfico de uma função cruza os eixos. Veremos alguns exemplos mais tarde.
Para a função\(f(x)=3x^2+10x−8\), encontre
ⓐ os zeros da função,
ⓑ qualquer\(x\) interceptação do gráfico da função
ⓒ qualquer\(y\) interceptação do gráfico da função
- Responda
-
ⓐ Para encontrar os zeros da função, precisamos descobrir quando o valor da função é 0.
\(\begin{array} {ll} &f(x)=3x^2+10x−8 \\ \text{Substitute }0\text{ for}f(x). &0=3x^2+10x−8 \\ \text{Factor the trinomial.} &(x+4)(3x−2)=0 \\ \begin{array} {l} \text{Use the zero product property.} \\ \text{Solve.} \end{array} &\begin{array} {lll} x+4=0 &\text{or} &3x−2=0 \\ x=−4 &\text{or} &x=\frac{2}{3} \end{array} \end{array}\)
ⓑ Uma\(x\) intercepção -ocorre quando\(y=0\). Desde\(f(−4)=0\) e\(f(\frac{2}{3})=0\), os pontos\((−4,0)\) e\((\frac{2}{3},0)\) estão no gráfico. Esses pontos são\(x\) -interceptos da função.
ⓒ Uma\(y\) intercepção -ocorre quando\(x=0\). Para encontrar as\(y\) interceptações -, precisamos encontrar\(f(0)\).
\(\begin{array} {ll} &f(x)=3x^2+10x−8 \\ \text{Find }f(0)\text{ by substituting }0\text{ for }x. &f(0)=3·0^2+10·0−8 \\ \text{Simplify.} &f(0)=−8 \end{array} \)
Desde então\(f(0)=−8\), o ponto\((0,−8)\) está no gráfico. Esse ponto é o\(y\) intercepto -da função.
Para a função\(f(x)=2x^2−7x+5\), encontre
ⓐ os zeros da função
ⓑ qualquer\(x\) interceptação do gráfico da função
ⓒ qualquer\(y\) interceptação do gráfico da função.
- Responda
-
ⓐ\(x=1\) ou\(x=\frac{5}{2}\)
ⓑ\((1,0),\space (\frac{5}{2},0)\) ⓒ\((0,5)\)
Para a função\(f(x)=6x^2+13x−15\), encontre
ⓐ os zeros da função
ⓑ qualquer\(x\) interceptação do gráfico da função
ⓒ qualquer\(y\) interceptação do gráfico da função.
- Responda
-
ⓐ\(x=−3\) ou\(x=\frac{5}{6}\)
ⓑ\((−3,0),\space (\frac{5}{6},0)\) ⓒ\((0,−15)\)
Resolva aplicações modeladas por equações polinomiais
A estratégia de resolução de problemas que usamos anteriormente para aplicativos que se traduzem em equações lineares também funcionará bem para aplicativos que se traduzem em equações polinomiais. Vamos copiar a estratégia de resolução de problemas aqui para que possamos usá-la como referência.
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
- Identifique o que estamos procurando.
- Diga o que estamos procurando. Escolha uma variável para representar essa quantidade.
- Traduza em uma equação. Pode ser útil reafirmar o problema em uma frase com todas as informações importantes. Em seguida, traduza a frase em inglês em uma equação algébrica.
- Resolva a equação usando técnicas de álgebra apropriadas.
- Verifique a resposta do problema e verifique se faz sentido.
- Responda à pergunta com uma frase completa.
Começaremos com um problema numérico para praticar a tradução de palavras em uma equação polinomial.
O produto de dois números inteiros ímpares consecutivos é 323. Encontre os números inteiros.
- Responda
-
\(\begin{array} {ll} \textbf{Step 1. Read }\text{the problem.} & \\ \textbf{Step 2. Identify }\text{what we are looking for.} &\text{We are looking for two consecutive integers.} \\ \textbf{Step 3. Name}\text{ what we are looking for.} &\text{Let } n=\text{ the first integer.} \\ &n+2= \text{ next consecutive odd integer} \\ \begin{array} {l} \textbf{Step 4. Translate }\text{into an equation. Restate the}\hspace{20mm} \\ \text{problem in a sentence.} \end{array} &\begin{array} {l} \text{The product of the two consecutive odd} \\ \text{integers is }323. \end{array} \\ &\quad n(n+2)=323 \\ \textbf{Step 5. Solve }\text{the equation.} n^2+2n=323 \\ \text{Bring all the terms to one side.} &n^2+2n−323=0 \\ \text{Factor the trinomial.} &(n−17)(n+19)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve the equations.} \end{array} &\begin{array} {ll} n−17=0 \hspace{10mm}&n+19=0 \\ n=17 &n=−19 \end{array} \end{array} \)
Existem dois valores para\(n\) que sejam soluções para esse problema. Portanto, existem dois conjuntos de números inteiros ímpares consecutivos que funcionarão.\(\begin{array} {ll} \text{If the first integer is } n=17 \hspace{60mm} &\text{If the first integer is } n=-19 \\ \text{then the next odd integer is} &\text{then the next odd integer is} \\ \hspace{53mm} n+2 &\hspace{53mm} n+2 \\ \hspace{51mm} 17+2 &\hspace{51mm} -19+2 \\ \hspace{55mm} 19 &\hspace{55mm} -17 \\ \hspace{51mm} 17,19 &\hspace{51mm} -17,-19 \\ \textbf{Step 6. Check }\text{the answer.} & \\ \text{The results are consecutive odd integers} & \\ \begin{array} {ll} 17,\space 19\text{ and }−19,\space −17. & \\ 17·19=323\checkmark &−19(−17)=323\checkmark \end{array} & \\ \text{Both pairs of consecutive integers are solutions.} & \\ \textbf{Step 7. Answer }\text{the question} &\text{The consecutive integers are }17, 19\text{ and }−19,−17. \end{array} \)
O produto de dois números inteiros ímpares consecutivos é 255. Encontre os números inteiros.
- Responda
-
\(−15,−17\)e\(15, 17\)
O produto de dois números inteiros ímpares consecutivos é 483 Encontre os números inteiros.
- Responda
-
\(−23,−21\)e\(21, 23\)
Você ficou surpreso com o par de números inteiros negativos que é uma das soluções para o exemplo anterior? O produto dos dois números inteiros positivos e o produto dos dois números inteiros negativos dão resultados positivos.
Em algumas aplicações, soluções negativas resultarão da álgebra, mas não serão realistas para a situação.
Um quarto retangular tem uma área de 117 pés quadrados. O comprimento do quarto é quatro pés a mais do que a largura. Encontre o comprimento e a largura do quarto.
- Responda
-
Etapa 1. Leia o problema. Em problemas envolvendo figuras
geométricas, um esboço pode ajudar você
a visualizar a situação.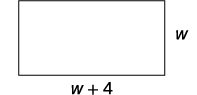
Etapa 2. Identifique o que você está procurando. Estamos procurando o comprimento e a largura. Etapa 3. Diga o que você está procurando. Deixe\(w=\text{ the width of the bedroom}\). O comprimento é quatro pés a mais do que a largura. \(w+4=\text{ the length of the garden}\) Etapa 4. Traduza em uma equação. Reafirme as informações importantes em uma frase. A área do quarto é de 117 pés quadrados. Use a fórmula para a área de um retângulo. \(A=l·w\) Substitua as variáveis. \(117=(w+4)w\) Etapa 5. Resolva a equação Distribuir primeiro. \(117=w^2+4w\) Obtenha zero em um lado. \(117=w^2+4w\) Considere o trinômio. \(0=w^2+4w−117\) Use a propriedade Zero Product. \(0=(w^2+13)(w−9)\) Resolva cada equação. \(0=w+13\quad 0=w−9\) Como\(w\) é a largura do quarto, não
faz sentido que seja negativo. Eliminamos esse valor para\(w\).\(\cancel{w=−13}\)\(\quad w=9\) \(w=9\)A largura é de 9 pés. Encontre o valor do comprimento. \(w+4\)
\(9+4\)
13 O comprimento é de 13 pés.Etapa 6. Verifique a resposta.
A resposta faz sentido?
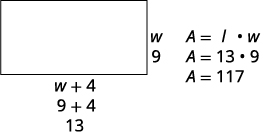
Sim, isso faz sentido.Etapa 7. Responda à pergunta. A largura do quarto é de 9 pés e
o comprimento é de 13 pés.
Uma placa retangular tem uma área de 30 pés quadrados. O comprimento da placa é um pé a mais do que a largura. Encontre o comprimento e a largura da placa.
- Responda
-
A largura é de 5 pés e o comprimento é de 6 pés.
Um pátio retangular tem uma área de 180 pés quadrados. A largura do pátio é três pés menor que o comprimento. Encontre o comprimento e a largura do pátio.
- Responda
-
O comprimento do pátio é de 12 pés e a largura de 15 pés.
No próximo exemplo, usaremos o Teorema de Pitágoras\((a^2+b^2=c^2)\). Essa fórmula fornece a relação entre as pernas e a hipotenusa de um triângulo reto.
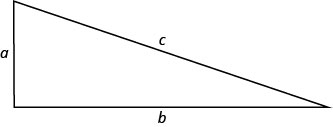
Usaremos essa fórmula para no próximo exemplo.
A vela de um barco tem a forma de um triângulo reto, conforme mostrado. A hipotenusa terá 17 pés de comprimento. O comprimento de um lado será 7 pés a menos que o comprimento do outro lado. Encontre os comprimentos dos lados da vela.
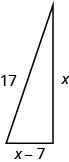
- Responda
-
Etapa 1. Leia o problema Etapa 2. Identifique o que você está procurando. Estamos procurando os comprimentos das
laterais da vela.Etapa 3. Diga o que você está procurando.
Um lado é 7 a menos que o outro.Deixe\(x=\text{ length of a side of the sail}\).
\(x−7=\text{ length of other side}\)Etapa 4. Traduza em uma equação. Como esse é um
triângulo reto, podemos usar o Teorema de Pitágoras.\(a^2+b^2=c^2\) Substitua as variáveis. \(x^2+(x−7)^2=17^2\) Etapa 5. Resolva a equação
Simplifique.\(x^2+x^2−14x+49=289\) \(2x^2−14x+49=289\) É uma equação quadrática, então obtenha zero em um lado. \(2x^2−14x−240=0\) Considere o maior fator comum. \(2(x^2−7x−120)=0\) Considere o trinômio. \(2(x−15)(x+8)=0\) Use a propriedade Zero Product. \(2\neq 0\quad x−15=0\quad x+8=0\) Resolver. \(2\neq 0\quad x=15\quad x=−8\) Como\(x\) é um lado do triângulo, não\(x=−8\)
faz sentido.\(2\neq 0\quad x=15\quad \cancel{x=−8}\) Encontre o comprimento do outro lado. Se o comprimento de um lado for
, então o comprimento do outro lado é


8 é o comprimento do outro lado.Etapa 6. Verifique a resposta no problema
Esses números fazem sentido?
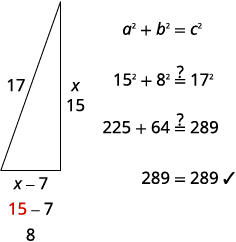
Etapa 7. Responda à pergunta Os lados da vela têm 8, 15 e 17 pés.
Justine quer colocar um baralho no canto de seu quintal em forma de triângulo reto. O comprimento de um lado do convés é 7 pés a mais do que o outro lado. A hipotenusa é 13. Encontre os comprimentos dos dois lados do baralho.
- Responda
-
5 pés e 12 pés
Um jardim de meditação tem a forma de um triângulo reto, com uma perna de 7 pés. O comprimento da hipotenusa é um a mais do que o comprimento da outra perna. Encontre o comprimento da hipotenusa e da outra perna.
- Responda
-
24 pés e 25 pés
O próximo exemplo usa a função que fornece a altura de um objeto em função do tempo quando ele é lançado de 80 pés acima do solo.
Dennis vai jogar sua bola de elástico para cima do topo de um prédio do campus. Quando ele joga a bola de elástico a 80 pés acima do solo, a função\(h(t)=−16t^2+64t+80\) modela a altura\(h\),, da bola acima do solo em função do tempo,\(t\). Encontre:
ⓐ os zeros dessa função que nos dizem quando a bola atinge o chão
ⓑ quando a bola estará 80 pés acima do solo
ⓒ a altura da bola em\(t=2\) segundos.
- Responda
-
ⓐ Os zeros dessa função são encontrados pela resolução\(h(t)=0\). Isso nos dirá quando a bola atingirá o chão.
\(\begin{array} {ll} &h(t)=0 \\ \text{Substitute in the polynomial for }h(t). &−16t^2+64t+80=0 \\ \text{Factor the GCF, }−16. &−16(t^2−4t−5)=0 \\ \text{Factor the trinomial.} &−16(t−5)(t+1)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve.} \end{array} &\begin{array} {ll} t−5=0 &t+1=0 \\ t=5 &t=−1 \end{array} \end{array} \)O resultado\(t=5\) indica que a bola atingirá o chão 5 segundos depois de ser lançada. Como o tempo não pode ser negativo, o resultado\(t=−1\) é descartado.
ⓑ A bola estará 80 pés acima do solo quando\(h(t)=80\).
\(\begin{array} {ll} &h(t)=80 \\ \text{Substitute in the polynomial for }h(t). &−16t^2+64t+80=80 \\ \text{Subtract 80 from both sides.} &−16t^2+64t=0 \\ \text{Factor the GCF, }−16t. &−16t(t−4)=0 \\ \begin{array} {l} \text{Use the Zero Product Property.} \\ \text{Solve.}\end{array} &\begin{array} {ll} −16t=0 &t−4=0 \\ t=0 &t=4 \end{array} \\ &\text{The ball will be at 80 feet the moment Dennis} \\ &\text{tosses the ball and then 4 seconds later, when} \\ &\text{the ball is falling.} \end{array} \)ⓒ Para encontrar a bola de altura em\(t=2\) segundos, encontramos\(h(2)\).
\(\begin{array} {ll} &h(t)=−16t^2+64t+80 \\ \text{To find }h(2)\text{ substitute }2\text{ for }t. &h(2)=−16(2)^2+64·2+80 \\ \text{Simplify.} &h(2)=144 \\ &\text{After 2 seconds, the ball will be at 144 feet.} \end{array}\)
Genevieve vai jogar uma pedra do topo de uma trilha com vista para o oceano. Quando ela joga a rocha para cima a partir de 160 pés acima do oceano, a função\(h(t)=−16t^2+48t+160\) modela a altura\(h\),, da rocha acima do oceano em função do tempo,\(t\). Encontre:
ⓐ os zeros dessa função que nos dizem quando a rocha atingirá o oceano
ⓑ quando a rocha estará 160 pés acima do oceano.
ⓒ a altura da rocha em\(t=1.5\) segundos.
- Responda
-
ⓐ 5 ⓑ 0; 3 ⓒ 196
Calib vai jogar seu centavo da sorte de sua varanda em um navio de cruzeiro. Quando ele joga o centavo para cima a partir de 128 pés acima do solo, a função\(h(t)=−16t^2+32t+128\) modela a altura\(h\),, do centavo acima do oceano em função do tempo,\(t\). Encontre:
ⓐ os zeros dessa função, que é quando o centavo atingirá o oceano
ⓑ quando o centavo estará 128 pés acima do oceano.
ⓒ a altura em que o centavo estará em\(t=1\) segundos, quando o centavo estará em seu ponto mais alto.
- Responda
-
ⓐ 4 ⓑ 0; 2 ⓒ 144
Acesse este recurso on-line para obter instruções e práticas adicionais com equações quadráticas.
Conceitos-chave
- Equação polinomial: Uma equação polinomial é uma equação que contém uma expressão polinomial. O grau da equação polinomial é o grau do polinômio.
- Equação quadrática: Uma equação da forma\(ax^2+bx+c=0\) é chamada de equação quadrática.
\[a,b,c\text{ are real numbers and } a\neq 0\nonumber\]
- Propriedade de produto zero: se\(a·b=0\), então um\(a=0\)\(b=0\) ou ambos.
- Como usar a propriedade Zero Product
- Defina cada fator igual a zero.
- Resolva as equações lineares.
- Confira.
- Como resolver uma equação quadrática por fatoração.
- Escreva a equação quadrática na forma padrão,\(ax^2+bx+c=0\).
- Considere a expressão quadrática.
- Use a propriedade Zero Product.
- Resolva as equações lineares.
- Confira. Substitua cada solução separadamente na equação original.
- Zero de uma função: Para qualquer função\(f\), if\(f(x)=0\), então\(x\) é um zero da função.
- Como usar uma estratégia de resolução de problemas para resolver problemas com palavras.
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
- Identifique o que estamos procurando.
- Diga o que estamos procurando. Escolha uma variável para representar essa quantidade.
- Traduza em uma equação. Pode ser útil reafirmar o problema em uma frase com todas as informações importantes. Em seguida, traduza a frase em inglês em uma equação algébrica.
- Resolva a equação usando técnicas de álgebra apropriadas.
- Verifique a resposta do problema e verifique se faz sentido.
- Responda à pergunta com uma frase completa.


