6.3: Fatores trinômios
- Page ID
- 183289
Ao final desta seção, você poderá:
- Trinômios fatoriais da forma\(x^2+bx+c\)
- Trinômios fatoriais do formulário\(ax^2+bx+c\) usando tentativa e erro
- Trinômios fatoriais da forma\(ax^2+bx+c\) usando o método\(ac\) ''
- Fator usando substituição
Antes de começar, faça este teste de prontidão.
Trinômios fatoriais da forma\(x^2+bx+c\)
Você já aprendeu como multiplicar binômios usando FOIL. Agora você precisará “desfazer” essa multiplicação. Fatorar o trinômio significa começar com o produto e terminar com os fatores.
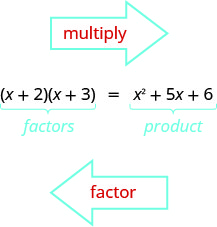
Para descobrir como fatoraríamos um trinômio da forma\(x^2+bx+c\), como\(x^2+5x+6\) e o fatoraríamos\((x+2)(x+3)\), vamos começar com dois binômios gerais da forma\((x+m)\)\((x+n)\) e.
| \((x+m)(x+n)\) | |
| Folha para encontrar o produto. | \(x^{2}+m x+n x+m n\) |
| Considere o GCF a partir dos termos intermediários. | \(x^{2}+(m+n) x+m n\) |
| Nosso trinômio é da forma\(x^2+bx+c\). | \(\overbrace{x^{2}+(m+n) x+m n}^{\color{red}x^{2}+b x+c}\) |
Isso nos diz que, para fatorar um trinômio da forma\(x^2+bx+c\), precisamos de dois fatores\((x+m)\) e\((x+n)\) onde os dois números\(m\)\(n\) se multiplicam\(c\) e somam\(b\).
Fator:\(x^2+11x+24\).
- Resposta
-




Fator:\(q^2+10q+24\).
- Resposta
-
\((q+4)(q+6)\)
Fator:\(t^2+14t+24\).
- Resposta
-
\((t+2)(t+12)\)
Vamos resumir as etapas que usamos para encontrar os fatores.
- Escreva os fatores como dois binômios com os primeiros termos x. \(\quad \begin{array} {l} x^2+bx+c \\ (x\quad)(x\quad) \end{array} \)
- Encontre dois números\(m\) e\(n\) isso
- multiplicar para\(c\),\(m·n=c\)
- adicionar a\(b\),\(m+n=b\)
- Use\(m\) e\(n\) como os últimos termos dos fatores. \(\quad (x+m)(x+n)\)
- Verifique multiplicando os fatores.
No primeiro exemplo, todos os termos no trinômio foram positivos. O que acontece quando há termos negativos? Bem, depende de qual termo é negativo. Vejamos primeiro os trinômios com apenas o termo médio negativo.
Como você obtém um produto positivo e uma soma negativa? Usamos dois números negativos.
Fator:\(y^2−11y+28\).
- Resposta
-
Novamente, com o último termo positivo e o médio prazo negativo\(−11y\), precisamos de dois fatores negativos.\(28\) Encontre dois números que se multiplicam\(28\) e se somam\(−11\) a.
\(\begin{array} {ll} &y^2−11y+28 \\ \text{Write the factors as two binomials with first terms }y. &( y \quad )( y \quad ) \\ \text{Find two numbers that: multiply to }28\text{ and add to }−11.\end{array}\)Fatores de\(28\) Soma dos fatores \ (28\)” data-valign="top">\(−1,\space −28\)
\(−2,\space −14\)
\(−4,\space −7\)\(−1+(−28)=−29\)
\(−2+(−14)=−16\)
\(−4+(−7)=−11^∗\)\(\begin{array} {ll} \text{Use }−4,\space −7\text{ as the last terms of the binomials.} &(y−4)(y−7) \\ \text{Check:} & \\ \hspace{30mm} (y−4)(y−7) & \\ \hspace{25mm} y^2−7y−4y+28 & \\ \hspace{30mm} y^2−11y+28\checkmark & \end{array} \)
Fator:\(u^2−9u+18\).
- Resposta
-
\((u−3)(u−6)\)
Fator:\(y^2−16y+63\).
- Resposta
-
\((y−7)(y−9)\)
Agora, e se o último termo no trinômio for negativo? Pense em FOIL. O último termo é o produto dos últimos termos nos dois binômios. Um produto negativo resulta da multiplicação de dois números por sinais opostos. Você deve ter muito cuidado ao escolher fatores para garantir que também obtenha o sinal correto para o médio prazo.
Como você obtém um produto negativo e uma soma positiva? Usamos um número positivo e um negativo.
Quando fatoramos os trinômios, devemos ter os termos escritos em ordem decrescente — na ordem do grau mais alto para o menor grau.
Fator:\(2x+x^2−48\).
- Resposta
-
\(\begin{array} {ll} &2x+x^2−48 \\ \text{First we put the terms in decreasing degree order.} &x^2+2x−48 \\ \text{Factors will be two binomials with first terms }x. &(x\quad)(x\quad) \end{array} \)
Fatores de −48−48 Soma dos fatores \(−1,\space 48\)
\(−2,\space 24\)
\(−3,\space 16\)
\(−4,\space 12\)
\(−6,\space 8\)\(−1+48=47\)
\(−2+24=22\)
\(−3+16=13\)
\(−4+12=8\)
\(−6+8=2^∗\)\(\begin{array} {ll} \text{Use }−6,\space 8\text{ as the last terms of the binomials.} &(x−6)(x+8) \\ \text{Check:} & \\ \hspace{30mm} (x−6)(x+8) & \\ \hspace{25mm} x^2−6q+8q−48 & \\ \hspace{30mm} x^2+2x−48\checkmark & \end{array} \)
Fator:\(9m+m^2+18\).
- Resposta
-
\((m+3)(m+6)\)
Fator:\(−7n+12+n^2\).
- Resposta
-
\((n−3)(n−4)\)
Às vezes, você precisará fatorar os trinômios do formulário\(x^2+bxy+cy^2\) com duas variáveis, como\(x^2+12xy+36y^2\). O primeiro termo\(x^2\),, é o produto dos primeiros termos dos fatores binomiais,\(x·x\). O\(y^2\) no último termo significa que os segundos termos dos fatores binomiais devem conter cada um\(y\). Para obter os coeficientes\(b\)\(c\), use o mesmo processo resumido em Como fatorar trinômios.
Fator:\(r^2−8rs−9s^2\).
- Resposta
-
Precisamos\(r\) no primeiro termo de cada binômio e\(s\) no segundo termo. O último termo do trinômio é negativo, então os fatores devem ter sinais opostos.
\(\begin{array} {ll} &r^2−8rs−9s^2 \\ \text{Note that the first terms are }r,\text{last terms contain }s. &(r\quad s)(r\quad s) \\ \text{Find the numbers that multiply to }−9\text{ and add to }−8. \end{array}\)Fatores de\(−9\) Soma dos fatores \ (−9\)” data-valign="top">\(1,\space −9\) \(−1+9=8\) \ (−9\)” data-valign="top">\(−1,\space 9\) \(1+(−9)=−8^∗\) \ (−9\)” data-valign="top">\(3,\space −3\) \(3+(−3)=0\) \(\begin{array} {ll} \text{Use }1,\space -9\text{ as coefficients of the last terms.} &(r+s)(r−9s) \\ \text{Check:} & \\ \hspace{30mm} (r−9s)(r+s) & \\ \hspace{25mm} r^2+rs−9rs−9s^2 & \\ \hspace{30mm} r^2−8rs−9s^2\checkmark & \end{array} \)
Fator:\(a^2−11ab+10b^2\).
- Resposta
-
\((a−b)(a−10b)\)
Fator:\(m^2−13mn+12n^2\).
- Resposta
-
\((m−n)(m−12n)\)
Alguns trinômios são primos. A única maneira de ter certeza de que um trinômio é primordial é listar todas as possibilidades e mostrar que nenhuma delas funciona.
Fator:\(u^2−9uv−12v^2\).
- Resposta
-
Precisamos\(u\) no primeiro termo de cada binômio e\(v\) no segundo termo. O último termo do trinômio é negativo, então os fatores devem ter sinais opostos.
\(\begin{array} {ll} &u^2−9uv−12v^2 \\ \text{Note that the first terms are }u,\text{ last terms contain }v. &(u\quad v)(u\quad v) \\ \text{Find the numbers that multiply to }−12\text{ and add to }−9. & \end{array} \)Fatores de\(−12\) Soma dos fatores \ (−12\)” data-valign="top">\(1,−12\)
\(−1,12\)
\(2,−6\)
\(−2,6\)
\(3,−4\)
\(−3,4\)\(1+(−12)=−11\)
\(−1+12=11\)
\(2+(−6)=−4\)
\(−2+6=4\)
\(3+(−4)=−1\)
\(−3+4=1\)Observe que não há pares de fatores que nos\(−9\) forneçam como soma. O trinômio é primordial.
Fator:\(x^2−7xy−10y^2\).
- Resposta
-
primo
Fator:\(p^2+15pq+20q^2\).
- Resposta
-
primo
Vamos resumir o método que acabamos de desenvolver para fatorar os trinômios da forma\(x^2+bx+c\).
Quando consideramos um trinômio, examinamos primeiro os sinais de seus termos para determinar os sinais dos fatores binomiais.
| \( x^{2}+b x+c \) | ||
| \( (x+m)(x+n) \) | ||
| Quando\( c \) é positivo\( m \) e\( n \) tem o mesmo sinal. | ||
| \( b \)positivo | \( b \)negativo | |
| \( m,n \)positivo | \( m,n \)negativo | |
| \( x^{2}+5 x+6 \) | \( x^{2}-6 x+8 \) | |
| \( (x+2)(x+3) \) | \( (x-4)(x-2) \) | |
| mesmos sinais | mesmos sinais | |
| Quando\( c \) é negativo\( m \) e\( n \) tem o sinal oposto. | ||
| \( x^{2}+x-12 \) | \( x^{2}-2 x-15 \) | |
| \( (x+4)(x-3) \) | \( (x-5)(x+3) \) | |
| sinais opostos | sinais opostos | |
Observe que, no caso em que\(m\) e\(n\) tenham sinais opostos, o sinal daquele com o maior valor absoluto corresponde ao sinal de\(b\).
Trinômios fatoriais da forma ax 2 + bx + c usando tentativa e erro
Nosso próximo passo é fatorar trinômios cujo coeficiente principal não é 1, trinômios da forma\(ax^2+bx+c\).
Lembre-se de sempre verificar primeiro se há um GCF! Às vezes, depois de fatorar o GCF, o coeficiente principal do trinômio se torna\(1\) e você pode fatorá-lo pelos métodos que usamos até agora. Vamos dar um exemplo para ver como isso funciona.
Fator completamente:\(4x^3+16x^2−20x\).
- Resposta
-
\(\begin{array} {lll} \text{Is there a greatest common factor?} &\qquad &4x^3+16x^2−20x \\ \quad \text{Yes, }GCF=4x.\text{ Factor it.} & &4x(x^2+4x−5) \\ & & \\ & & \\ \text{Binomial, trinomial, or more than three terms?} & & \\ \quad \text{It is a trinomial. So “undo FOIL.”} & &4x(x\quad)(x\quad) \\ & & \\ & & \\ \text{Use a table like the one shown to find two numbers that} & &4x(x−1)(x+5) \\ \text{multiply to }−5\text{ and add to }4. & & \\ & & \\ & & \end{array} \)
Fatores de\(−5\) Soma dos fatores \ (−5\)” data-valign="top">\(−1,5\)
\(1,−5\)\(−1+5=4^∗\)
\(1+(−5)=−4\)\(\begin{array} {l} \text{Check:}\\ \hspace{27mm}4x(x−1)(x+5) \\ \hspace{25mm} 4x(x^2+5x−x−5) \\ \hspace{30mm} 4x(x^2+4x−5) \\ \hspace{25mm} 4x^3+16x2−20x\checkmark \end{array} \)
Fator completamente:\(5x^3+15x^2−20x\).
- Resposta
-
\(5x(x−1)(x+4)\)
Fator completamente:\(6y^3+18y^2−60y\).
- Resposta
-
\(6y(y−2)(y+5)\)
O que acontece quando o coeficiente principal não é\(1\) e não há GCF? Existem vários métodos que podem ser usados para fatorar esses trinômios. Primeiro, usaremos o método de tentativa e erro.
Vamos considerar o trinômio\(3x^2+5x+2\).
De nosso trabalho anterior, esperamos que isso seja considerado em dois binômios.
\[3x^2+5x+2\nonumber\]\[(\quad)(\quad)\nonumber\]
Sabemos que os primeiros termos dos fatores binomiais se multiplicarão para nos dar\(3x^2\). Os únicos fatores do\(3x^2\) são\(1x,\space 3x\). Podemos colocá-los nos binômios.
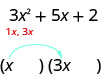
Verifique: Faz\(1x·3x=3x^2\)?
Sabemos que os últimos termos dos binômios se multiplicarão para\(2\). Como esse trinômio tem todos os termos positivos, precisamos apenas considerar fatores positivos. Os únicos fatores de\(2\) são\(1\)\(2\) e. Mas agora temos dois casos a considerar, pois fará diferença se escrevermos\(1\),\(2\) ou\(2\),\(1\).

Quais fatores estão corretos? Para decidir isso, multiplicamos os termos interno e externo.
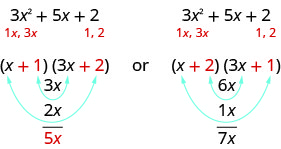
Como o termo médio do trinômio é\(5x\), os fatores no primeiro caso funcionarão. Vamos usar FOIL para verificar.
\[(x+1)(3x+2)\nonumber\]\[3x^2+2x+3x+2\nonumber\]\[3x^2+5x+2\checkmark\nonumber\]
Nosso resultado da fatoração é:
\[3x^2+5x+2\nonumber\]\[(x+1)(3x+2)\nonumber\]
Considere completamente usando tentativa e erro:\(3y^2+22y+7\).
- Resposta
-






Considere completamente usando tentativa e erro:\(2a^2+5a+3\).
- Resposta
-
\((a+1)(2a+3)\)
Considere completamente usando tentativa e erro:\(4b^2+5b+1\).
- Resposta
-
\((b+1)(4b+1)\)
- Escreva o trinômio em ordem decrescente de graus, conforme necessário.
- Fator qualquer GCF.
- Encontre todos os pares de fatores do primeiro termo.
- Encontre todos os pares de fatores do terceiro termo.
- Teste todas as combinações possíveis dos fatores até que o produto correto seja encontrado.
- Verifique multiplicando.
Lembre-se de que, quando o termo médio é negativo e o último termo é positivo, os sinais nos binômios devem ser negativos.
Considere completamente usando tentativa e erro:\(6b^2−13b+5\).
- Resposta
-
O trinômio já está em ordem decrescente. 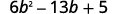
Encontre os fatores do primeiro termo. 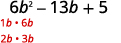
Encontre os fatores do último período. Considere os sinais.
Como o último termo\(5\),, é positivo, seus fatores devem ser
positivos ou negativos. O coeficiente do termo
médio é negativo, então usamos os fatores negativos.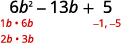
Considere todas as combinações de fatores.
\(6b^2−13b+5\) Fatores possíveis Produto \ (6b^2−13b+5\) Fatores possíveis” data-valign="top">\((b−1)(6b−5)\) \ (6b^2−13b+5\) Produto” data-valign="top">\(6b^2−11b+5\) \ (6b^2−13b+5\) Fatores possíveis” data-valign="top">\((b−5)(6b−1)\) \ (6b^2−13b+5\) Produto” data-valign="top">\(6b^2−31b+5\) \ (6b^2−13b+5\) Fatores possíveis” data-valign="top">\((2b−1)(3b−5)\) \ (6b^2−13b+5\) Produto” data-valign="middle">\(6b^2−13b+5^∗\) \ (6b^2−13b+5\) Fatores possíveis” data-valign="top">\((2b−5)(3b−1)\) \ (6b^2−13b+5\) Produto” data-valign="middle">\(6b^2−17b+5\) \(\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial.} &(2b−1)(3b−5) \\ \text{Check by multiplying:} & \\ \hspace{50mm} (2b−1)(3b−5) & \\ \hspace{47mm} 6b^2−10b−3b+5 & \\ \hspace{50mm} 6b^2−13b+5\checkmark & \end{array} \)
Considere completamente usando tentativa e erro:\(8x^2−14x+3\).
- Resposta
-
\((2x−3)(4x−1)\)
Considere completamente usando tentativa e erro:\(10y^2−37y+7\).
- Resposta
-
\((2y−7)(5y−1)\)
Quando consideramos uma expressão, sempre procuramos primeiro o maior fator comum. Se a expressão não tiver o maior fator comum, também não pode haver um em seus fatores. Isso pode nos ajudar a eliminar algumas das combinações possíveis de fatores.
Considere completamente usando tentativa e erro:\(18x^2−37xy+15y^2\).
- Resposta
-
O trinômio já está em ordem decrescente. 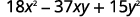
Encontre os fatores do primeiro termo. 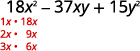
Encontre os fatores do último período. Considere os sinais.
Como 15 é positivo e o coeficiente do médio
prazo é negativo, usamos os fatores negativos.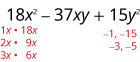
Considere todas as combinações de fatores.

\(\begin{array} {ll} \text{The correct factors are those whose product is} & \\ \text{the original trinomial.} &(2x−3y)(9x−5y) \\ \text{Check by multiplying:} & \\ & \\ & \\ & \\ \hspace{50mm} (2x−3y)(9x−5y) & \\ \hspace{45mm}18x^2−10xy−27xy+15y^2 & \\ \hspace{47mm}18x^2−37xy+15y^2\checkmark & \end{array} \)
Considere completamente usando tentativa e erro\(18x^2−3xy−10y^2\).
- Resposta
-
\((3x+2y)(6x−5y)\)
Considere completamente usando tentativa e erro:\(30x^2−53xy−21y^2\).
- Resposta
-
\((3x+y)(10x−21y)\)
Não se esqueça de procurar primeiro um GCF e lembre-se se o coeficiente principal é negativo, assim como o GCF.
Considere completamente usando tentativa e erro:\(−10y^4−55y^3−60y^2\).
- Resposta
-
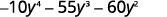
Observe o maior fator comum, então considere-o primeiro. 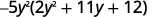
Considere o trinômio. 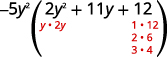
Considere todas as combinações.
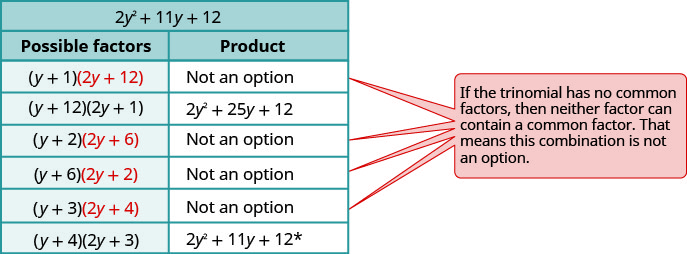
-
\(\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial. Remember to include} & \\ \text{the factor }−5^y2. &−5y^2(y+4)(2y+3) \\ \text{Check by multiplying:} & \\ \hspace{50mm} −5y^2(y+4)(2y+3) & \\ \hspace{45mm} −5y^2(2y^2+8y+3y+12) & \\ \hspace{47mm}−10y^4−55y^3−60y^2\checkmark & \end{array} \)
Considere completamente usando tentativa e erro:\(15n^3−85n^2+100n\).
- Resposta
-
\(5n(n−4)(3n−5)\)
Considere completamente usando tentativa e erro:\(56q^3+320q^2−96q\).
- Resposta
-
\(8q(q+6)(7q−2)\)
Trinômios fatoriais da forma\(ax^2+bx+c\) usando o método “\(ac\)”
Outra forma de fatorar os trinômios da forma\(ax^2+bx+c\) é o método “\(ac\)”. (O método “\(ac\)” às vezes é chamado de método de agrupamento.) O método “\(ac\)” é, na verdade, uma extensão dos métodos que você usou na última seção para fatorar trinômios com o coeficiente inicial um. Esse método é muito estruturado (passo a passo) e sempre funciona!
Fator usando o método “\(ac\)”:\(6x^2+7x+2\).
- Resposta
-






Fator usando o método “\(ac\)”:\(6x^2+13x+2\).
- Resposta
-
\((x+2)(6x+1)\)
Fator usando o método “\(ac\)”:\(4y^2+8y+3\).
- Resposta
-
\((2y+1)(2y+3)\)
O método “\(ac\)” está resumido aqui.
- Fator qualquer GCF.
- Encontre o produto\(ac\).
- Encontre dois números\(m\) e\(n\) isso:
\(\begin{array} {ll} \text{Multiply to }ac &m·n=a·c \\ \text{Add to }b &m+n=b \\ &ax^2+bx+c \end{array} \) - Divida o termo intermediário usando\(m\)\(n\) e. \(ax^2+mx+nx+c\)
- Fator por agrupamento.
- Verifique multiplicando os fatores.
Não se esqueça de procurar um fator comum!
Fator usando o método '“\(ac\)”:\(10y^2−55y+70\).
- Resposta
-
Existe um fator comum maior? Sim. O GCF é\(5\). 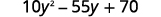
Fator isso. 
O trinômio dentro dos parênteses tem um coeficiente
principal que não é\(1\).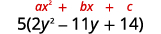
Encontre o produto\(ac\). \(ac=28\) Encontre dois números que se multiplicam por\(ac\) \((−4)(−7)=28\) e adicione\(b\) a. \(−4(−7)=−11\) Divida o meio termo. 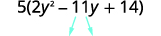
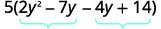
Fatore o trinômio por agrupamento. 
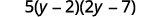
Verifique multiplicando todos os três fatores.
\(\hspace{50mm} 5(y−2)(2y−7)\)\(\hspace{45mm} 5(2y^2−7y−4y+14)\)
\(\hspace{48mm} 5(2y^2−11y+14)\)
\(\hspace{49mm} 10y^2−55y+70\checkmark\)
Fator usando o método “\(ac\)”:\(16x^2−32x+12\).
- Resposta
-
\(4(2x−3)(2x−1)\)
Fator usando o método “\(ac\)”:\(18w^2−39w+18\).
- Resposta
-
\(3(3w−2)(2w−3)\)
Fator usando substituição
Às vezes, um trinômio não parece estar na\(ax^2+bx+c\) forma. No entanto, muitas vezes podemos fazer uma substituição cuidadosa que nos permitirá ajustá-la ao\(ax^2+bx+c\) formulário. Isso é chamado de fatoração por substituição. É padrão\(u\) para uso na substituição.
No\(ax^2+bx+c\), o termo intermediário tem uma variável,\(x\), e seu quadrado\(x^2\),, é a parte variável do primeiro termo. Procure esse relacionamento ao tentar encontrar um substituto.
Fator por substituição:\(x^4−4x^2−5\).
- Resposta
-
A parte variável do termo médio é\(x^2\) e seu quadrado,\(x^4\), é a parte variável do primeiro termo. (Nós sabemos\((x^2)^2=x^4)\). Se deixarmos\(u=x^2\), podemos colocar nosso trinômio na\(ax^2+bx+c\) forma que precisamos para fatorá-lo.
\(x^4−4x^2−5\) Reescreva o trinômio para se preparar para a substituição. \((x^2)^2−4(x^2)-5\) Deixe\(u=x^2\) e substitua. \((u)^2−4(u)-5\) Considere o trinômio. \((u+1)(u-5)\) \(u\)Substitua por\(x^2\). \((x^2+1)(x^2-5)\) Confira:
\(\begin{array} {l} \hspace{37mm} (x^2+1)(x^2−5) \\ \hspace{35mm}x^4−5x^2+x^2−5 \\ \hspace{40mm}x^4−4x^2−5\checkmark\end{array}\)
Fator por substituição:\(h^4+4h^2−12\).
- Resposta
-
\((h^2−2)(h^2+6)\)
Fator por substituição:\(y^4−y^2−20\).
- Resposta
-
\((y^2+4)(y^2−5)\)
Às vezes, a expressão a ser substituída não é um monômio.
Fator por substituição:\((x−2)^2+7(x−2)+12\)
- Resposta
-
O binômio, no termo médio,\((x−2)\) é quadrado no primeiro termo. Se deixarmos\(u=x−2\) e substituirmos, nosso trinômio estará em\(ax^2+bx+c\) forma.
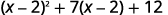
Reescreva o trinômio para se preparar para a substituição. 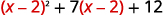
Deixe\(u=x−2\) e substitua. 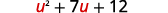
Considere o trinômio. 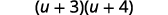
\(u\)Substitua por\(x−2\). 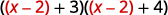
Simplifique dentro dos parênteses. 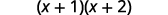
Isso também pode ser fatorado multiplicando primeiro o\((x−2)^2\) e o\(7(x−2)\) e, em seguida, combinando termos semelhantes e depois fatorando. A maioria dos estudantes prefere o método de substituição.
Fator por substituição:\((x−5)^2+6(x−5)+8\).
- Resposta
-
\((x−3)(x−1)\)
Fator por substituição:\((y−4)^2+8(y−4)+15\).
- Resposta
-
\((y−1)(y+1)\)
Assista a este vídeo para obter instruções adicionais e praticar a fatoração.
Conceitos chave
- Como fatorar os trinômios do formulário\(x^2+bx+c\).
- Escreva os fatores como dois binômios com os primeiros termos x. \(\quad \begin{array} (l) x^2+bx+c \\ (x\quad)(x\quad)\end{array}\)
- Encontre dois números\(m\) e\(n\) isso
\(\begin{array} {ll} \text{multiply to} &c,\space m·n=c \\ \text{add to} &b,\space m+n=b\end{array}\) - Use\(m\) e\(n\) como os últimos termos dos fatores. \(\qquad (x+m)(x+n)\)
- Verifique multiplicando os fatores.
- Estratégia para fatorar trinômios da forma\(x^2+bx+c\): Quando fatoramos um trinômio, examinamos primeiro os sinais de seus termos para determinar os sinais dos fatores binomiais.
Para trinômios da forma:\(x^2+bx+c = (x+m)(x+n)\)
Quando\(c\) é positivo\(m\) e\(n\) deve ter o mesmo sinal (e este será o sinal de\(b\) ).
Exemplos:\(x^2+5x+6=(x+2)(x+3)\),\(x^2−6x+8 = (x−4)(x−2)\)
Quando\(c\) é negativo\(m\) e\(n\) tem sinais opostos. O maior\(m\) e\(n\) terá o sinal de\(b\).
Exemplos:\(x^2+x−12=(x+4)(x−3)\),\(x^2−2x−15=(x−5)(x+3)\)
Observe que, no caso de sinais opostos\(m\) e\(n\) quando houver sinais opostos, o sinal daquele com o maior valor absoluto corresponde ao sinal de\(b\). - Como fatorar os trinômios do formulário\(ax^2+bx+c\) usando tentativa e erro.
- Escreva o trinômio em ordem decrescente de graus, conforme necessário.
- Fator qualquer GCF.
- Encontre todos os pares de fatores do primeiro termo.
- Encontre todos os pares de fatores do terceiro termo.
- Teste todas as combinações possíveis dos fatores até que o produto correto seja encontrado.
- Verifique multiplicando.
- Como fatorar os trinômios do formulário\(ax^2+bx+c\) usando o método “\(ac\)”.
- Fator qualquer GCF.
- Encontre o produto\(ac\).
- Encontre dois números\(m\) e\(n\) isso:
\(\begin{array} {ll} \text{Multiply to }ac. &m·n=a·c \\ \text{Add to }b. &m+n=b \\ &ax^2+bx+c\end{array}\) - Divida o termo intermediário usando\(m\)\(n\) e. \(\quad ax^2+mx+nx+c\)
- Fator por agrupamento.
- Verifique multiplicando os fatores.


