5.5: Dividindo polinômios
- Page ID
- 183256
Ao final desta seção, você poderá:
- Dividindo monômios
- Dividindo um polinômio por um monômio
- Divisão de polinômios usando divisão longa
- Divisão de polinômios usando divisão sintética
- Dividindo funções polinomiais
- Use os teoremas do restante e dos fatores
Antes de começar, faça este teste de prontidão.
Dividindo monômios
Agora estamos familiarizados com todas as propriedades dos expoentes e as usamos para multiplicar polinômios. Em seguida, usaremos essas propriedades para dividir monômios e polinômios.
Encontre o quociente:\(54a^2b^3÷ (−6ab^5)\).
Solução
Quando dividimos monômios com mais de uma variável, escrevemos uma fração para cada variável.
\(\begin{array} {ll} {} &{54a^2b^3÷(−6ab^5)} \\[5pt] {\text{Rewrite as a fraction.}} &{\dfrac{54a^2b^3}{−6ab^5}} \\[5pt] {\text{Use fraction multiplication.}} &{\dfrac{54}{−6}·\dfrac{a^2}{a}·\dfrac{b^3}{b^5}} \\[5pt] {\text{Simplify and use the Quotient Property.}} &{−9·a·\dfrac{1}{b^2}} \\[5pt] {\text{Multiply.}} &{−\dfrac{9a}{b^2}} \end{array}\)
Encontre o quociente:\(−72a^7b^3÷(8a^{12}b^4)\).
- Resposta
-
\(−\dfrac{9}{a^5b}\)
Encontre o quociente:\(−63c^8d^3÷(7c^{12}d^2)\).
- Resposta
-
\(\dfrac{−9d}{c^4}\)
Depois de se familiarizar com o processo e praticá-lo passo a passo várias vezes, você poderá simplificar uma fração em uma etapa.
Encontre o quociente:\(\dfrac{14x^7y^{12}}{21x^{11}y^6}\).
Solução
Tenha muito cuidado para simplificar\(\dfrac{14}{21}\) dividindo um fator comum e simplificar as variáveis subtraindo seus expoentes.
\(\begin{array} {ll} {} &{\dfrac{14x^7y^{12}}{21x^{11}y^6}} \\ {\text{Simplify and use the Quotient Property.}} &{\dfrac{2y^6}{3x^4}} \\ \end{array}\)
Encontre o quociente:\(\dfrac{28x^5y^{14}}{49x^9y^{12}}\).
- Resposta
-
\(\dfrac{4y^2}{7x^4}\)
Encontre o quociente:\(\dfrac{30m^5n^{11}}{48m^{10}n^{14}}\).
- Resposta
-
\(\dfrac{5}{8m^5n^3}\)
Divida um polinômio por um monômio
Agora que sabemos como dividir um monômio por um monômio, o próximo procedimento é dividir um polinômio de dois ou mais termos por um monômio. O método que usaremos para dividir um polinômio por um monômio é baseado nas propriedades da adição de frações. Então, começaremos com um exemplo para revisar a adição de frações. A soma\(\dfrac{y}{5}+\dfrac{2}{5}\) se simplifica para\(\dfrac{y+2}{5}\). Agora faremos isso ao contrário para dividir uma única fração em frações separadas. Por exemplo,\(\dfrac{y+2}{5}\) pode ser escrito\(\dfrac{y}{5}+\dfrac{2}{5}\).
Esse é o “inverso” da adição de frações e afirma que se a, b e c são números onde\(c\neq 0\), então\(\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\). Usaremos isso para dividir polinômios por monômios.
Para dividir um polinômio por um monômio, divida cada termo do polinômio pelo monômio.
Encontre o quociente:\((18x^3y−36xy^2)÷(−3xy)\).
Solução
\(\begin{array} {ll} {} &{(18x^3y−36xy^2)÷(−3xy)} \\[5pt] {\text{Rewrite as a fraction.}} &{\dfrac{18x^3y−36xy^2}{−3xy}} \\[5pt] {\text{Divide each term by the divisor. Be careful with the signs!}} &{\dfrac{18x^3y}{−3xy}−\dfrac{36xy^2}{−3xy}} \\[5pt] {\text{Simplify.}} &{−6x^2+12y} \end{array}\)
Encontre o quociente:\((32a^2b−16ab^2)÷(−8ab)\).
- Resposta
-
\(−4a+2b\)
Encontre o quociente:\((−48a^8b^4−36a^6b^5)÷(−6a^3b^3)\).
- Resposta
-
\(8a^5b+6a^3b^2\)
Divida polinômios usando divisão longa
Dividindo um polinômio por um binômio, seguimos um procedimento muito semelhante à divisão longa de números. Então, vamos examinar cuidadosamente os passos que tomamos quando dividimos um número de 3 dígitos, 875, por um número de 2 dígitos, 25.
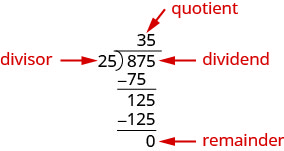
Verificamos a divisão multiplicando o quociente pelo divisor. Se fizermos a divisão corretamente, o produto deve ser igual ao dividendo.
\[\begin{array} {l} {35·25} \\ {875\checkmark} \\ \nonumber \end{array}\]
Agora vamos dividir um trinômio por um binômio. Ao ler o exemplo, observe como as etapas são semelhantes às do exemplo numérico acima.
Encontre o quociente:\((x^2+9x+20)÷(x+5)\).
Solução
| \(\require{enclose}\) | \(\qquad (x^2+9x+20) \div (x+5)\) |
| Escreva isso como um problema de divisão longa. Certifique-se de que o dividendo esteja no formato padrão. |
\(\qquad x+5\enclose{longdiv}{ x^2+9x+20\phantom{0}} \) |
|
Divida\(x^2\) por\(x\). Pode ser útil perguntar a si mesmo: “\(x\)Por que |
\(\qquad \begin{array}{r} {\color{red}x}\hspace{2.3em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{ {\color{red}x^2}+9x+20\phantom{0}} \end{array}\) |
| Coloque a resposta\(x\),, no quociente sobre o\(x\) termo. Multiplique\(x\) vezes\(x+5\). Alinhe os termos similares sob o dividendo. |
\(\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+9x+20\phantom{0}}\\[-3pt] \underline{\color{red}x^2+5x}\hspace{2.4em} \end{array}\) |
| Subtraia\(x^2+5x\) de\(x^2+9x\). Você pode achar mais fácil alterar os sinais e depois adicionar. Em seguida, derrube o último termo,\(20.\) |
\(\qquad \begin{array}{r}x\hspace{2.3em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x+20}\hspace{0.5em} \end{array}\) |
Divida\(4x\) por\(x\). Pode ser útil perguntar a si mesmo: “\(x\)Por que preciso multiplicar para conseguir\(4x\)?” Coloque a resposta\(4\),, no quociente sobre o termo constante. |
\(\qquad \begin{array}{r}x+\phantom{0}{\color{red}4}\hspace{.5em}\\[-3pt] {\color{red}x}+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] {\color{red}4x}+20\hspace{0.5em} \end{array}\) |
| Multiplique 4 vezes\(x+5\). |
\(\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{0.5em}\\[-3pt] \underline{ \color{red}4x+20}\hspace{.5em} \end{array}\) |
| Subtraia\(4x+20\) de\(4x+20\). |
\(\qquad \begin{array}{r}x+\phantom{0}4\hspace{.5em}\\[-3pt] x+5\enclose{longdiv}{x^2+\phantom{00}9x+20\phantom{0}}\\[-3pt] \underline{{\color{red}-}x^2+({\color{red}-}5x)}\hspace{2.1em}\\[-3pt] 4x+20\hspace{.5em}\\[-3pt] \underline{{\color{red}-}4x+({\color{red}-}20)}\\[-3pt] 0\hspace{.33em}\end{array}\) |
|
Confira: \(\begin{array} {ll} {\text{Multiply the quotient by the divisor.}} &{(x+4)(x+5)} \\ {\text{You should get the dividend.}} &{x^2+9x+20\checkmark}\\ \end{array}\) |
Encontre o quociente:\((y^2+10y+21)÷(y+3)\).
- Resposta
-
\(y+7\)
Encontre o quociente:\((m^2+9m+20)÷(m+4)\).
- Resposta
-
\(m+5\)
Quando dividimos 875 por 25, não tínhamos resto. Mas às vezes a divisão de números deixa um resto. O mesmo acontece quando dividimos polinômios. No próximo exemplo, teremos uma divisão que deixa um restante. Escrevemos o restante como uma fração com o divisor como denominador.
Examine os dividendos nos exemplos anteriores. Os termos foram escritos em ordem decrescente de graus e não faltavam graus. O dividendo neste exemplo será\(x^4−x^2+5x−6\). Está faltando um\(x^3\) termo. Vamos adicionar\(0x^3\) como um espaço reservado.
Encontre o quociente:\((x^4−x^2+5x−6)÷(x+2)\).
Solução
Observe que não há\(x^3\) prazo no dividendo. Vamos adicionar\(0x^3\) como um espaço reservado.
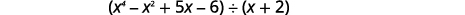 |
|
| Escreva isso como um problema de divisão longa. Certifique-se de que o dividendo esteja no formato padrão com espaços reservados para termos ausentes. | 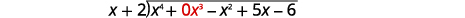 |
| Divida\(x^4\) por\(x\). Coloque a resposta\(x^3\),, no quociente sobre o\(x^3\) termo. Multiplique\(x^3\) vezes\(x+2\). Alinhe os termos semelhantes. Subtraia e, em seguida, reduza o próximo termo. |
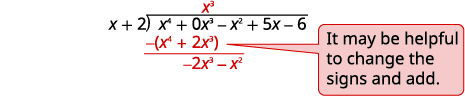 |
| Divida\(−2x^3\) por\(x\). Coloque a resposta\(−2x^2\),, no quociente sobre o\(x^2\) termo. Multiplique\(−2x^2\) vezes\(x+1\). Alinhe os termos semelhantes Subtrair e reduza o próximo termo. |
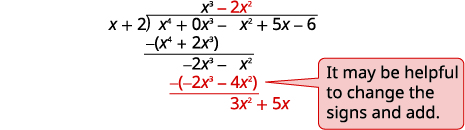 |
| Divida\(3x^2\) por\(x\). Coloque a resposta\(3x\),, no quociente sobre o\(x\) termo. Multiplique\(3x\) vezes\(x+1\). Alinhe os termos semelhantes. Subtraia e reduza o próximo termo. |
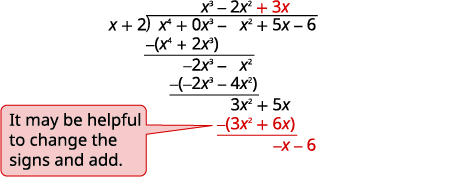 |
| Divida\(−x\) por\(x\). Coloque a resposta\(−1\),, no quociente sobre o termo constante. Multiplique\(−1\) vezes\(x+1\). Alinhe os termos semelhantes. Mude os sinais, adicione. Escreva o restante como uma fração com o divisor como denominador. |
 |
| Para verificar, multiplique\((x+2)(x^3−2x^2+3x−1−4x+2)\). O resultado deve ser\(x^4−x^2+5x−6\). |
Encontre o quociente:\((x^4−7x^2+7x+6)÷(x+3)\).
- Resposta
-
\(x^3−3x^2+2x+1+3x+3\)
Encontre o quociente:\((x^4−11x^2−7x−6)÷(x+3)\).
- Resposta
-
\(x^3−3x^2−2x−1−3x+3\)
No próximo exemplo, dividiremos por\(2a−3\). À medida que dividimos, teremos que considerar as constantes e as variáveis.
Encontre o quociente:\((8a^3+27)÷(2a+3)\).
Solução
Desta vez, mostraremos a divisão em uma única etapa. Precisamos adicionar dois espaços reservados para dividi-los.
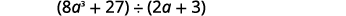 |
|
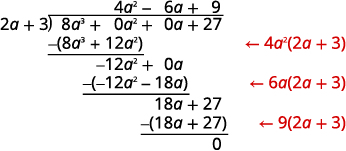 |
Para verificar, multiplique\((2a+3)(4a^2−6a+9)\).
O resultado deve ser\(8a^3+27\).
Encontre o quociente:\((x^3−64)÷(x−4)\).
- Resposta
-
\(x^2+4x+16\)
Encontre o quociente:\((125x^3−8)÷(5x−2)\).
- Resposta
-
\(25x^2+10x+4\)
Divida polinômios usando divisão sintética
Como mencionamos anteriormente, os matemáticos gostam de encontrar padrões para facilitar seu trabalho. Como a divisão longa pode ser entediante, vamos analisar a divisão longa que fizemos no Example e procurar alguns padrões. Usaremos isso como base para o que é chamado de divisão sintética. O mesmo problema no formato de divisão sintética é mostrado a seguir.
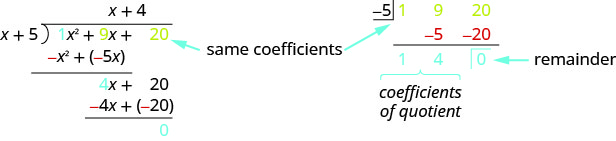
A divisão sintética basicamente remove variáveis e números repetidos desnecessários. Aqui, todos os\(x\) e\(x^2\) são removidos. bem como os\(−x^2\) e\(−4x\), pois são opostos ao termo acima.
- A primeira linha da divisão sintética são os coeficientes do dividendo. O\(−5\) é o oposto do 5 no divisor.
- A segunda linha da divisão sintética são os números mostrados em vermelho no problema da divisão.
- A terceira linha da divisão sintética são os números mostrados em azul no problema da divisão.
Observe que o quociente e o restante são mostrados na terceira linha.
\[\text{Synthetic division only works when the divisor is of the form }x−c. \nonumber \]
O exemplo a seguir explicará o processo.
Use a divisão sintética para encontrar o quociente e o restante quando\(2x^3+3x^2+x+8\) é dividido por\(x+2\).
Solução
| Escreva o dividendo com poderes decrescentes de\(x\). | 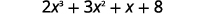 |
| Escreva os coeficientes dos termos como a primeira linha da divisão sintética. |
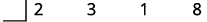 |
| Escreva o divisor como\(x−c\) e coloque c na divisão sintética na caixa do divisor. |
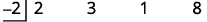 |
| Reduza o primeiro coeficiente para a terceira linha. | 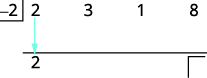 |
| Multiplique esse coeficiente pelo divisor e coloque o resultado na segunda linha abaixo do segundo coeficiente. |
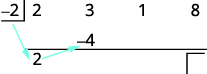 |
| Adicione a segunda coluna, colocando o resultado na terceira linha. | 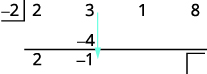 |
| Multiplique esse resultado pelo divisor e coloque o resultado na segunda linha abaixo do terceiro coeficiente. |
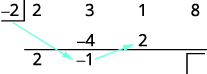 |
| Adicione a terceira coluna, colocando o resultado na terceira linha. | 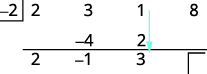 |
| Multiplique esse resultado pelo divisor e coloque o resultado na terceira linha abaixo do terceiro coeficiente. |
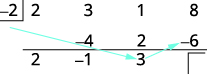 |
| Adicione a coluna final, colocando o resultado na terceira linha. | 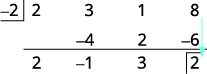 |
| O quociente é\(2x^2−1x+3\) e o restante é 2. |
A divisão está completa. Os números na terceira linha nos dão o resultado. \(2\space\space\space−1\space\space\space3\)São os coeficientes do quociente. O quociente é\(2x^2−1x+3\). O 2 na caixa na terceira linha é o restante.
Confira:
\(\begin{align} (\text{quotient})(\text{divisor}) + \text{remainder} &= \text{dividend} \nonumber\\ (2x^2−1x+3)(x+2)+2 &\overset{?}{=} 2x^3+3x^2+x+8 \nonumber\\ 2x^3−x^2+3x+4x^2−2x+6+2 &\overset{?}{=} 2x^3+3x^2+x+8 \nonumber\\ 2x^3+3x^2+x+8 &= 2x^3+3x^2+x+8\checkmark \nonumber \end{align} \)
Use a divisão sintética para encontrar o quociente e o restante quando\(3x^3+10x^2+6x−2\) é dividido por\(x+2\).
- Resposta
-
\(3x^2+4x−2;\space 2\)
Use a divisão sintética para encontrar o quociente e o restante quando\(4x^3+5x^2−5x+3\) é dividido por\(x+2\).
- Resposta
-
\(4x^2−3x+1; 1\)
No próximo exemplo, faremos todas as etapas juntos.
Use a divisão sintética para encontrar o quociente e o restante quando\(x^4−16x^2+3x+12\) é dividido por\(x+4\).
Solução
O polinômio\(x^4−16x^2+3x+12\) tem seu termo em ordem decrescente, mas notamos que não há nenhum\(x^3\) termo. Adicionaremos um 0 como espaço reservado para o\(x^3\) termo. Na\(x−c\) forma, o divisor é\(x−(−4)\).
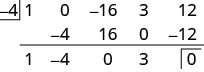
Dividimos um\(4^{\text{th}}\) polinômio de\(1^{\text{st}}\) grau por um polinômio de grau para que o quociente seja um polinômio de\(3^{\text{rd}}\) grau.
Lendo a partir da terceira linha, o quociente tem os coeficientes\(1\space\space\space−4\space\space\space0\space\space\space3\), que é\(x^3−4x^2+3\). O restante
é 0.
Use a divisão sintética para encontrar o quociente e o restante quando\(x^4−16x^2+5x+20\) é dividido por\(x+4\).
- Resposta
-
\(x^3−4x^2+5;\space 0\)
Use a divisão sintética para encontrar o quociente e o restante quando\(x^4−9x^2+2x+6\) é dividido por\(x+3\).
- Resposta
-
\(x^3−3x^2+2;\space 0\)
Divida funções polinomiais
Assim como os polinômios podem ser divididos, as funções polinomiais também podem ser divididas.
Para funções\(f(x)\) e\(g(x)\), onde\(g(x)\neq 0\),
\[\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)} \nonumber\]
Para funções\(f(x)=x^2−5x−14\) e\(g(x)=x+2\), encontre:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−4)\).
Solução
ⓐ
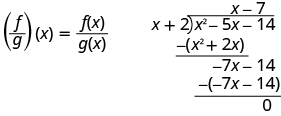
\(\begin{array} {ll} {\text{Substitute for }f(x)\text{ and }g(x).} &{\left(\dfrac{f}{g}\right)(x)=\dfrac{x^2−5x−14}{x+2}} \\[5pt] {\text{Divide the polynomials.}} &{\left(\dfrac{f}{g}\right)(x)=x−7} \end{array} \)
ⓑ Em parte ⓐ encontramos\(\left(\dfrac{f}{g}\right)(x)\) e agora somos convidados a encontrar\(\left(\dfrac{f}{g}\right)(−4)\).
\(\begin{array} {ll} {} &{\left(\dfrac{f}{g}\right)(x)=x−7} \\[5pt] {\text{To find }\left(\dfrac{f}{g}\right)(−4), \text{ substitute }x=−4.} &{\left(\dfrac{f}{g}\right)(−4)=−4−7} \\[5pt] {} &{\left(\dfrac{f}{g}\right)(−4)=−11} \end{array}\)
Para funções\(f(x)=x^2−5x−24\) e\(g(x)=x+3\), encontre:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−3)\).
- Responda a
-
\(\left(\dfrac{f}{g}\right)(x)=x−8\)
- Resposta b
-
\(\left(\dfrac{f}{g}\right)(−3)=−11\)
Para funções\(f(x)=x2−5x−36\) e\(g(x)=x+4\), encontre:
- \(\left(\dfrac{f}{g}\right)(x)\)
- \(\left(\dfrac{f}{g}\right)(−5)\).
- Responda a
-
\(\left(\dfrac{f}{g}\right)(x)=x−9\)
- Resposta b
-
\(\left(\dfrac{f}{g}\right)(x)=x−9\)
Use o Teorema do Resto e do Fator
Vamos dar uma olhada nos problemas de divisão que acabamos de resolver e que acabaram com o restante. Eles estão resumidos no gráfico abaixo. Se pegarmos o dividendo de cada problema de divisão e o usarmos para definir uma função, obteremos as funções mostradas no gráfico. Quando o divisor é escrito como\(x−c\), o valor da função at\(c\),\(f(c)\), é o mesmo que o restante do problema de divisão.
| Dividendo | Divisor\(x−c\) | Restante | Função | \(f(c)\) |
|---|---|---|---|---|
| \(x^4−x^2+5x−6\) | \ (x−c\)” data-valign="top">\(x−(−2)\) | \(−4\) | \(f(x)=x^4−x^2+5x−6\) | \ (f (c)\)” data-valign="top">\(−4\) |
| \(3x^3−2x^2−10x+8\) | \ (x−c\)” data-valign="top">\(x−2\) | 4 | \(f(x)=3x^3−2x^2−10x+8\) | \ (f (c)\)” data-valign="top">4 |
| \(x^4−16x^2+3x+15\) | \ (x−c\)” data-valign="top">\(x−(−4)\) | 3 | \(f(x)=x^4−16x^2+3x+15\) | \ (f (c)\)” data-valign="top">3 |
Para ver isso de forma mais geral, percebemos que podemos verificar um problema de divisão multiplicando o quociente pelo divisor e adicionando o restante. Na notação de função, poderíamos dizer que\(f(x)\), para obter o dividendo, multiplicamos o quociente,\(q(x)\) vezes o divisor\(x−c\), e adicionamos o restante\(r\).
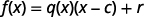 |
|
| Se avaliarmos isso em\(c\), obteremos: | 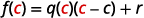 |
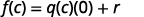 |
|
 |
Isso nos leva ao Teorema do Restante.
Se a função polinomial\(f(x)\) for dividida por\(x−c\), o restante será\(f(c)\).
Use o Teorema do Restante para encontrar o restante quando\(f(x)=x^3+3x+19\) é dividido por\(x+2\).
Solução
Para usar o Teorema do Restante, devemos usar o divisor no\(x−c\) formulário. Podemos escrever o divisor\(x+2\) como\(x−(−2)\). Então, o nosso\(c\) é\(−2\).
Para encontrar o restante, avaliamos\(f(c)\) qual é\(f(−2)\).
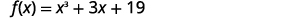 |
|
| Para avaliar\(f(−2)\), substitua\(x=−2\). | 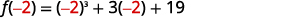 |
| Simplifique. | 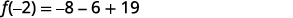 |
 |
|
| O restante é 5 quando\(f(x)=x^3+3x+19\) é dividido por\(x+2\). | |
| Verificação: Use divisão sintética para verificar. |
|
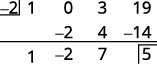 |
|
| O restante é 5. |
Use o Teorema do Restante para encontrar o restante quando\(f(x)=x^3+4x+15\) é dividido por\(x+2\).
- Resposta
-
\(−1\)
Use o Teorema do Restante para encontrar o restante quando\(f(x)=x^3−7x+12\) é dividido por\(x+3\).
- Resposta
-
\(6\)
Quando dividimos\(8a^3+27\) por\(2a+3\) em Exemplo, o resultado foi\(4a^2−6a+9\). Para conferir nosso trabalho, multiplicamos\(4a2−6a+9\) por\(2a+3\) para obter\(8a^3+27\).
\[(4a^2−6a+9)(2a+3)=8a^3+27 \nonumber \]
Escrito dessa forma, podemos ver isso\(4a^2−6a+9\) e\(2a+3\) são fatores de\(8a^3+27\). Quando fizemos a divisão, o restante foi zero.
Sempre que um divisor\(x−c\),, divide uma função polinomial,\(f(x)\), e resulta em um restante de zero, dizemos que\(x−c\) é um fator de\(f(x)\).
O inverso também é verdadeiro. Se\(x−c\) for um fator de\(f(x)\), então\(x−c\) dividirá a função polinomial, resultando em um restante de zero.
Vamos afirmar isso no Teorema do Fator.
Para qualquer função polinomial\(f(x)\),
- se\(x−c\) é um fator de\(f(x)\), então\(f(c)=0\)
- se\(f(c)=0\), então\(x−c\) é um fator de\(f(x)\)
Use o Teorema do Restante para determinar se\(x−4\) é um fator de\(f(x)=x^3−64\).
Solução
O Teorema do Fator nos diz que isso\(x−4\) é um fator de\(f(x)=x^3−64\) se\(f(4)=0\).
\(\begin{array} {ll} {} &{f(x)=x^3−64} \\[5pt] {\text{To evaluate }f(4) \text{ substitute } x=4.} &{f(4)=4^3−64} \\[5pt] {\text{Simplify.}} &{f(4)=64−64} \\[5pt]{\text{Subtract.}} &{f(4)=0} \end{array}\)
Uma vez que\(f(4)=0, x−4\) é um fator de\(f(x)=x^3−64\).
Use o Teorema do Fator para determinar se\(x−5\) é um fator de\(f(x)=x^3−125\).
- Resposta
-
sim
Use o Teorema do Fator para determinar se\(x−6\) é um fator de\(f(x)=x^3−216\).
- Resposta
-
sim
Acesse esses recursos on-line para obter instruções adicionais e praticar a divisão de polinômios.
- Dividindo um polinômio por um binômio
- Divisão sintética e teorema do resto
Conceitos-chave
- Divisão de um polinômio por um monômio
- Para dividir um polinômio por um monômio, divida cada termo do polinômio pelo monômio.
- Divisão de funções polinomiais
- Para funções\(f(x)\) e\(g(x)\), onde\(g(x)\neq 0\),
\(\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)}\)
- Para funções\(f(x)\) e\(g(x)\), onde\(g(x)\neq 0\),
- Teorema do Restante
- Se a função polinomial\(f(x)\) for dividida por\(x−c\), o restante será\(f(c)\).
- Teorema do fator: Para qualquer função polinomial\(f(x)\),
- se\(x−c\) é um fator de\(f(x)\), então\(f(c)=0\)
- se\(f(c)=0\), então\(x−c\) é um fator de\(f(x)\)


