Skip to main content
Global

2.7: Resolver desigualdades compostas

  1. Last updated
  2. Save as PDF
  • Page ID
    183674

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    objetivos de aprendizagem

    Ao final desta seção, você poderá:

    • Resolva desigualdades compostas com “e”
    • Resolva desigualdades compostas com “ou”
    • Resolva aplicativos com desigualdades compostas

    Antes de começar, faça este teste de prontidão.

    1. Simplifique:\(\frac{2}{5}(x+10)\).
      Se você perdeu esse problema, revise [link].
    2. Simplifique:\(−(x−4)\).
      Se você perdeu esse problema, revise [link].

    Resolva desigualdades compostas com “e”

    Agora que sabemos como resolver desigualdades lineares, o próximo passo é analisar as desigualdades compostas. Uma desigualdade composta é composta por duas desigualdades conectadas pela palavra “e” ou pela palavra “ou”. Por exemplo, a seguir estão as desigualdades compostas.

    \[\begin{array} {lll} {x+3>−4} &{\text{and}} &{4x−5\leq 3} \\ {2(y+1)<0} &{\text{or}} &{y−5\geq −2} \\ \end{array} \nonumber\]

    DESIGUALDADE COMPOSTA

    Uma desigualdade composta é composta por duas desigualdades conectadas pela palavra “e” ou pela palavra “ou”.

    Resolver uma desigualdade composta significa encontrar todos os valores da variável que fazem da desigualdade composta uma afirmação verdadeira. Resolvemos desigualdades compostas usando as mesmas técnicas que usamos para resolver desigualdades lineares. Resolvemos cada desigualdade separadamente e depois consideramos as duas soluções.

    Para resolver uma desigualdade composta com a palavra “e”, procuramos todos os números que tornem ambas as desigualdades verdadeiras. Para resolver uma desigualdade composta com a palavra “ou”, procuramos todos os números que tornam a desigualdade verdadeira.

    Vamos começar com as desigualdades compostas com “e”. Nossa solução serão os números que são soluções para ambas as desigualdades conhecidas como a interseção das duas desigualdades. Considere a interseção de duas ruas — a parte em que as ruas se sobrepõem — pertence às duas ruas.

    A figura é uma ilustração de duas ruas com sua interseção sombreada

    Para encontrar a solução de uma desigualdade composta “e”, examinamos os gráficos de cada desigualdade e, em seguida, encontramos os números que pertencem aos dois gráficos, onde os gráficos se sobrepõem.

    Para a desigualdade composta\(x>−3\) e\(x\leq 2\), representamos graficamente cada desigualdade. Em seguida, procuramos onde os gráficos “se sobrepõem”. Os números sombreados em ambos os gráficos serão sombreados no gráfico da solução da desigualdade composta. Veja a Figura\(\PageIndex{1}\).

    A figura mostra que o gráfico de x é maior que menos 3 com um parêntese esquerdo em menos 3 e sombreado à direita, o gráfico de x é menor ou igual a 2 com um colchete em 2 e sombreado à esquerda, e o gráfico de x é maior que menos 3 e x é menor ou igual a 2 com um parêntese esquerdo em menos 3 e um parêntese direito em 2 e sombreamento entre menos 3 e 2. Menos 3 e 2 são marcados por linhas em cada linha numérica.
    Figura\(\PageIndex{1}\)

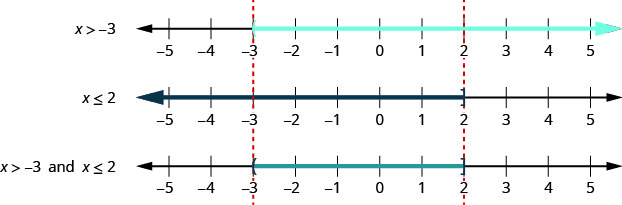
    Podemos ver que os números entre\(−3\) e\(2\) estão sombreados nos dois primeiros gráficos. Em seguida, eles serão sombreados no gráfico da solução.

    O número não\(−3\) está sombreado no primeiro gráfico e, como não está sombreado nos dois gráficos, ele não está incluído no gráfico da solução.

    O número dois está sombreado no primeiro e no segundo gráfico. Portanto, ele será sombreado no gráfico da solução.

    É assim que mostraremos nossa solução nos próximos exemplos.

    Exemplo\(\PageIndex{1}\)

    Resolva\(6x−3<9\)\(2x+7\geq 3\) e. Faça um gráfico da solução e escreva a solução em notação de intervalo.

    Resposta
      \(6x−3<9\) e \(2x+9\geq 3\)
    Etapa 1. Resolva cada
    desigualdade.    		 \(6x−3<9\)   \(2x+9\geq 3\)
      \(6x<12\)   \(2x\geq −6\)
      \(x<2\) e \(x\geq −3\)
    Etapa 2. Faça um gráfico de cada solução. Em seguida, faça um gráfico dos números que tornam as duas desigualdades verdadeiras. O gráfico final mostrará todos os números que tornam as duas desigualdades verdadeiras — os números sombreados nos dois primeiros gráficos. .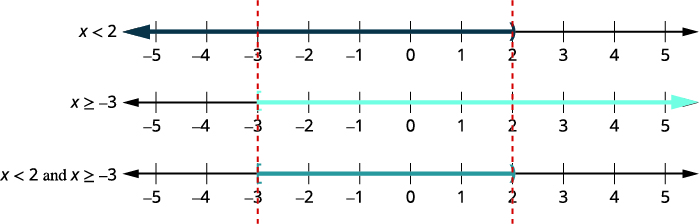
    Etapa 3. Escreva a solução em notação de intervalo. \([−3,2)\)
    Todos os números que tornam as duas desigualdades verdadeiras são a solução para a desigualdade composta.
    Exemplo\(\PageIndex{2}\)

    Resolva a desigualdade composta. Faça um gráfico da solução e escreva a solução em notação de intervalo:\(4x−7<9\)\(5x+8\geq 3\) e.

    Resposta

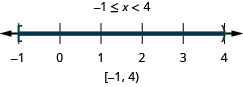
    A solução é menos 1 é menor ou igual a x, que é menor que 4. Em uma reta numérica, ela é mostrada com um círculo fechado em menos 1 e um círculo aberto em 4 com sombreamento entre os círculos fechados e abertos. Sua notação de intervalo é de menos 1 a 4 dentro de um colchete e um parêntese.

    Exemplo\(\PageIndex{3}\)

    Resolva a desigualdade composta. Faça um gráfico da solução e escreva a solução em notação de intervalo:\(3x−4<5\)\(4x+9\geq 1\) e.

    Resposta

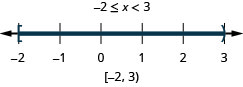
    A solução é menos 2 é menor ou igual a x, que é menor que 3. Em uma reta numérica, ela é mostrada com um círculo fechado em menos 2 e um círculo aberto em 3 com sombreamento entre os círculos fechados e abertos. Sua notação de intervalo é de menos 2 a 3 dentro de um colchete e um parêntese.

    RESOLVA UMA DESIGUALDADE COMPOSTA COM “E”.
    1. Resolva cada desigualdade.
    2. Faça um gráfico de cada solução. Em seguida, faça um gráfico dos números que tornam as duas desigualdades verdadeiras.
      Este gráfico mostra a solução para a desigualdade composta.
    3. Escreva a solução em notação de intervalo.
    Exemplo\(\PageIndex{4}\)

    Resolva\(3(2x+5)\leq 18\)\(2(x−7)<−6\) e. Faça um gráfico da solução e escreva a solução em notação de intervalo.

    Resposta
      \(3(2x+5)\leq 18\) e \(2(x−7)<−6\)
    Resolva cada
    desigualdade.    		 \(6x+15\leq 18\)   \(2x−14<−6\)
      \(6x\leq 3\)   \(2x<8\)
      \(x\leq \frac{1}{2}\) e \(x<4\)
    Faça um gráfico de cada
    solução.    		 .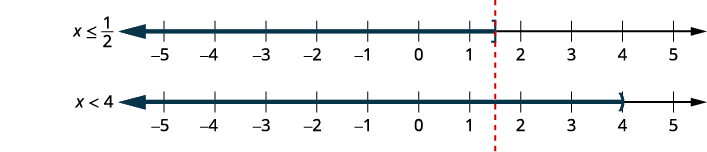
    Faça um gráfico dos números
    que tornam as duas
    desigualdades verdadeiras.    		 .
    Escreva a solução
    em notação de intervalo.    		 \((−\infty, \frac{1}{2}]\)
    Exemplo\(\PageIndex{5}\)

    Resolva a desigualdade composta. Faça um gráfico da solução e escreva a solução em notação de intervalo:\(2(3x+1)\leq 20\)\(4(x−1)<2\) e.

    Resposta

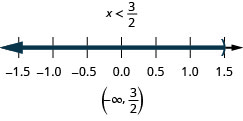
    A solução é x é menor que três metades. Em uma reta numérica, ela é mostrada com um círculo aberto em três metades com sombreamento à esquerda. Sua notação de intervalo é de menos infinito a três metades dentro de parênteses.

    Exemplo\(\PageIndex{6}\)

    Resolva a desigualdade composta. Faça um gráfico da solução e escreva a solução em notação de intervalo:\(5(3x−1)\leq 10\)\(4(x+3)<8\) e.

    Resposta

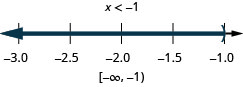
    A solução é x é menor que menos 1. Em uma reta numérica, ela é mostrada com um círculo aberto em 1 com sombreamento à esquerda. Sua notação de intervalo é de menos infinito a menos 1 entre parênteses.

    Exemplo\(\PageIndex{7}\)

    Resolva\(\frac{1}{3}x−4\geq −2\)\(−2(x−3)\geq 4\) e. Faça um gráfico da solução e escreva a solução em notação de intervalo.

    Resposta
      \(\frac{1}{3}x−4\geq −2\) e \(−2(x−3)\geq 4\)
    Resolva cada desigualdade. \(\frac{1}{3}x−4\geq −2\)   \(−2x+6\geq 4\)
      \(\frac{1}{3}x\geq 2\)   \(−2x\geq −2\)
      \(x\geq 6\) e \(x\leq 1\)
    Faça um gráfico de cada solução. ...
    Faça um gráfico dos números que
    tornam as duas desigualdades
    verdadeiras.    		 ...
      Não há números que tornem as duas desigualdades verdadeiras.

    Isso é uma contradição, então não há solução. Não há números que tornem as duas desigualdades verdadeiras.

    Isso é uma contradição, então não há solução. Não há números que tornem as duas desigualdades verdadeiras.

    Isso é uma contradição, então não há solução.
    Exemplo\(\PageIndex{8}\)

    Resolva a desigualdade composta. Faça um gráfico da solução e escreva a solução em notação de intervalo:\(\frac{1}{4}x−3\geq −1\)\(−3(x−2)\geq 2\) e.

    Resposta

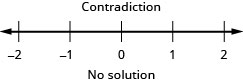
    A desigualdade é uma contradição. Então, não há solução. Como resultado, não há gráfico da linha numérica ou notação de intervalo.

    Exemplo\(\PageIndex{9}\)

    Resolva a desigualdade composta. Faça um gráfico da solução e escreva a solução em notação de intervalo:\(\frac{1}{5}x−5\geq −3\)\(−4(x−1)\geq −2\) e.

    Resposta

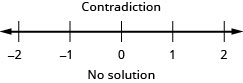
    A desigualdade é uma contradição. Então, não há solução. Como resultado, não há nenhum gráfico ou a notação de linha numérica ou intervalo.

    Às vezes, temos uma desigualdade composta que pode ser escrita de forma mais concisa. Por exemplo,\(a<x\) e\(x<b\) pode ser escrito simplesmente como\(a<x<b\) e então chamamos isso de dupla desigualdade. As duas formas são equivalentes.

    DESIGUALDADE DUPLA

    Uma desigualdade dupla é uma desigualdade composta, como\(a<x<b\). É equivalente a\(a<x\)\(x<b\) e.

    \[\text{Other forms:} \quad \begin{array} {lllll} {a<x<b} &{\text{is equivalent to }} &{a<x} &{\text{and}} &{x<b} \\ {a\leq x\leq b} &{\text{is equivalent to }} &{a\leq x} &{\text{and}} &{x\leq b} \\ {a>x>b} &{\text{is equivalent to }} &{a>x} &{\text{and}} &{x>b} \\ {a\geq x\geq b} &{\text{is equivalent to }} &{a\geq x} &{\text{and}} &{x\geq b} \\ \end{array} \nonumber\]

    Para resolver uma desigualdade dupla, realizamos a mesma operação em todas as três “partes” da dupla desigualdade com o objetivo de isolar a variável no centro.

    Exemplo\(\PageIndex{10}\)

    Resolver\(−4\leq 3x−7<8\). Faça um gráfico da solução e escreva a solução em notação de intervalo.

    Resposta
      \(-4 \leq 3x - 7 < 8\)
    Adicione 7 às três partes. \( -4 \,{\color{red}{+\, 7}} \leq 3x - 7 \,{\color{red}{+ \,7}} < 8 \,{\color{red}{+ \,7}}\)
    Simplifique. \( 3 \le 3x < 15 \)
    Divida cada parte por três. \( \dfrac{3}{\color{red}{3}} \leq \dfrac{3x}{\color{red}{3}} < \dfrac{15}{\color{red}{3}} \)
    Simplifique. \( 1 \leq x < 5 \)
    Faça um gráfico da solução. .
    Escreva a solução em notação de intervalo. \( [1, 5) \)

    Quando escrito como uma dupla desigualdade\(1\leq x<5\), é fácil ver que as soluções são os números entre um e cinco, incluindo um, mas não cinco. Em seguida, podemos representar graficamente a solução imediatamente, como fizemos acima.

    Outra forma de representar graficamente a solução de\(1\leq x<5\) é representar graficamente a solução de\(x\geq 1\) e a solução de\(x<5\). Em seguida, encontraríamos os números que tornam as duas desigualdades verdadeiras, como fizemos nos exemplos anteriores.

    Exemplo\(\PageIndex{11}\)

    Resolva a desigualdade composta. Faça um gráfico da solução e escreva a solução em notação de intervalo:\(−5\leq 4x−1<7\).

    Resposta

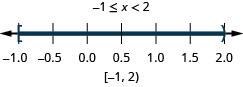
    A solução é menos 1 é menor ou igual a x, que é menor que 2. Seu gráfico tem um círculo fechado em menos 1 e um círculo aberto em 2 com sombreamento entre os círculos fechados e abertos. Sua notação de intervalo é de menos 1 a 2 dentro de um colchete e um parêntese.

    Exemplo\(\PageIndex{12}\)

    Resolva a desigualdade composta. Faça um gráfico da solução e escreva a solução em notação de intervalo:\(−3<2x−5\leq 1\).

    Resposta

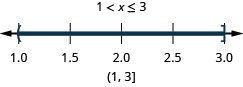
    A solução é 1 é menor que x, que é menor ou igual a 3. Seu gráfico tem um círculo aberto em 1 e um círculo fechado em 3 com sombreamento entre os círculos fechados e abertos. Sua notação de intervalo é de menos 1 a 3 dentro de um parêntese e um colchete.

    Resolva desigualdades compostas com “ou”

    Para resolver uma desigualdade composta com “ou”, começamos da mesma forma que fizemos com as desigualdades compostas com “e” — resolvemos as duas desigualdades. Em seguida, encontramos todos os números que tornam qualquer desigualdade verdadeira.

    Assim como os Estados Unidos são a união de todos os 50 estados, a solução será a união de todos os números que tornam qualquer desigualdade verdadeira. Para encontrar a solução da desigualdade composta, examinamos os gráficos de cada desigualdade, encontramos os números que pertencem a qualquer gráfico e juntamos todos esses números.

    Para escrever a solução em notação de intervalo, geralmente usaremos o símbolo de união\(\cup\),, para mostrar a união das soluções mostradas nos gráficos.

    RESOLVA UMA DESIGUALDADE COMPOSTA COM “OU”.
    1. Resolva cada desigualdade.
    2. Faça um gráfico de cada solução. Em seguida, faça um gráfico dos números que tornam qualquer desigualdade verdadeira.
    3. Escreva a solução em notação de intervalo.
    Exemplo\(\PageIndex{13}\)

    Resolva\(5−3x\leq −1\) ou\(8+2x\leq 5\). Faça um gráfico da solução e escreva a solução em notação de intervalo.

    Resposta
      \(5−3x\leq −1\) ou \(8+2x\leq 5\)
    Resolva cada desigualdade. \(5−3x\leq −1\)   \(8+2x\leq 5\)
      \(−3x\leq −6\)   \(2x\leq −3\)
      \(x\geq 2\) ou \(x\leq −\frac{3}{2}\)
    Faça um gráfico de cada solução. .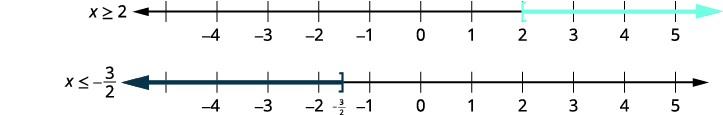
    Faça um gráfico de números que
    tornam qualquer desigualdade
    verdadeira.    		 .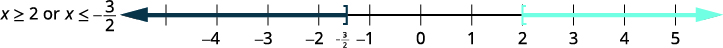
      \((−\infty,−32]\cup[2,\infty)\)
    Exemplo\(\PageIndex{14}\)

    Resolva a desigualdade composta. Faça um gráfico da solução e escreva a solução em notação de intervalo:\(1−2x\leq −3\) ou\(7+3x\leq 4\).

    Resposta

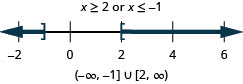
    A solução é x é maior ou igual a 2 ou x é menor ou igual a 1. O gráfico das soluções em uma reta numérica tem um círculo fechado em menos 1 e sombreado à esquerda e um círculo fechado em 2 com sombreamento à direita. A notação de intervalo é a união de menos infinito com menos 1 dentro de um parêntese e um colchete e 2 e infinito dentro de um colchete e um parêntese.

    Exemplo\(\PageIndex{15}\)

    Resolva a desigualdade composta. Faça um gráfico da solução e escreva a solução em notação de intervalo:\(2−5x\leq −3\) ou\(5+2x\leq 3\).

    Resposta

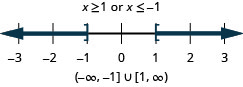
    A solução é x é maior ou igual a 1 ou x é menor ou igual a menos 1. O gráfico das soluções em uma reta numérica tem um círculo fechado em menos 1 e sombreado à esquerda e um círculo fechado em 1 com sombreamento à direita. A notação de intervalo é a união de menos infinito com menos 1 dentro de um parêntese e um colchete e 1 e infinito dentro de um colchete e um parêntese.

    Exemplo\(\PageIndex{16}\)

    Resolva\(\frac{2}{3}x−4\leq 3\) ou\(\frac{1}{4}(x+8)\geq −1\). Faça um gráfico da solução e escreva a solução em notação de intervalo.

    Resposta
      \(\frac{2}{3}x−4\leq 3\) ou \(\frac{1}{4}(x+8)\geq −1\)
    Resolva cada
    desigualdade.    		 \(3(\frac{2}{3}x−4)\leq 3(3)\)   \(4⋅\frac{1}{4}(x+8)\geq 4⋅(−1)\)
      \(2x−12\leq 9\)   \(x+8\geq −4\)
      \(2x\leq 21\)   \(x\geq −12\)
      \(x\leq \frac{21}{2}\)    
      \(x\leq \frac{21}{2}\) ou \(x\geq −12\)
    Faça um gráfico de cada
    solução.    		 .
    Faça um gráfico de números
    que tornam qualquer
    desigualdade verdadeira.    		 .
      A solução abrange todos os números reais.
      \((−\infty ,\infty )\)
    Exemplo\(\PageIndex{17}\)

    Resolva a desigualdade composta. Faça um gráfico da solução e escreva a solução em notação de intervalo:\(\frac{3}{5}x−7\leq −1\) ou\(\frac{1}{3}(x+6)\geq −2\).

    Resposta

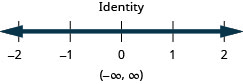
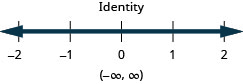
    A solução é uma identidade. Sua solução na reta numérica é sombreada para todos os valores. A solução na notação de intervalo é de menos infinito a infinito entre parênteses.

    Exemplo\(\PageIndex{18}\)

    Resolva a desigualdade composta. Faça um gráfico da solução e escreva a solução em notação de intervalo:\(\frac{3}{4}x−3\leq 3\) ou\(\frac{2}{5}(x+10)\geq 0\).

    Resposta

    A solução é uma identidade. Sua solução na reta numérica é sombreada para todos os valores. A solução na notação de intervalo é de menos infinito a infinito entre parênteses.

    Resolva aplicativos com desigualdades compostas

    Situações no mundo real também envolvem desigualdades compostas. Usaremos a mesma estratégia de resolução de problemas que usamos para resolver aplicações de equações lineares e desigualdades.

    Lembre-se de que as estratégias de solução de problemas são primeiro ler o problema e garantir que todas as palavras sejam compreendidas. Em seguida, identifique o que estamos procurando e atribua uma variável para representá-lo. Em seguida, reafirme o problema em uma frase para facilitar a tradução em uma desigualdade composta. Por último, resolveremos a desigualdade composta.

    Exemplo\(\PageIndex{19}\)

    Devido à seca na Califórnia, muitas comunidades têm taxas de água escalonadas. Existem taxas diferentes para uso de conservação, uso normal e uso excessivo. O uso é medido no número de cem pés cúbicos (hcf) que o proprietário usa.

    Durante o verão, o proprietário do imóvel pagará $24,72 mais $1,54 por hcf pelo uso normal. A fatura de uso normal seria entre ou igual a $57,06 e $171,02. Quantos hcf o proprietário pode usar se quiser que seu uso permaneça na faixa normal?

    Resposta
    Identifique o que estamos procurando. O número de hcf que ele pode usar e permanece na faixa de cobrança de “uso normal”.
    Diga o que estamos procurando. Seja x=x= o número de hcf que ele pode usar.
    Traduz-se em uma desigualdade. Bill é $24,72 mais $1.54 vezes o número de hcf que ele usa ou\(24.72+1.54x\).
     

    \(\color{Cerulean}{\underbrace{\color{black}{\text{His bill will be between or equal to }$57.06\text{ and }$171.02.}}}\)

    \(57.06 \leq 24.74 + 1.54x \leq 171.02 \)
    Resolva a desigualdade.

    \(57.06 \leq 24.74 + 1.54x \leq 171.02\)

    \(57.06 \,{\color{red}{- \,24.72}}\leq 24.74 \,{\color{red}{- \,24.72}} + 1.54x \leq 171.02 \,{\color{red}{- \,24.72}}\)

    \( 32.34 \leq 1.54x \leq 146.3\)

    \( \dfrac{32.34}{\color{red}{1.54}} \leq \dfrac{1.54x}{\color{red}{1.54}} \leq \dfrac{146.3}{\color{red}{1.54}}\)

    \( 21 \leq x \leq 95 \)
    Responda à pergunta. O proprietário do imóvel pode usar o\(21–95\) hcf e ainda se enquadrar na faixa de cobrança de “uso normal”.
    Exemplo\(\PageIndex{20}\)

    Devido à seca na Califórnia, muitas comunidades agora têm taxas de água escalonadas. Existem taxas diferentes para uso de conservação, uso normal e uso excessivo. O uso é medido no número de cem pés cúbicos (hcf) que o proprietário usa.

    Durante o verão, o proprietário do imóvel pagará $24,72 mais $1,32 por hcf pelo uso de conservação. A fatura para o Uso de Conservação seria entre ou igual a $31,32 e $52,12. Quantos hcf o proprietário pode usar se quiser que seu uso permaneça na área de conservação?

    Resposta

    O proprietário pode usar o\(5–20\) hcf e ainda se enquadrar na faixa de cobrança de “uso de conservação”.

    Exemplo\(\PageIndex{21}\)

    Devido à seca na Califórnia, muitas comunidades têm taxas de água escalonadas. Existem taxas diferentes para uso de conservação, uso normal e uso excessivo. O uso é medido no número de cem pés cúbicos (hcf) que o proprietário usa.

    Durante o inverno, o proprietário do imóvel pagará $24,72 mais $1,54 por hcf pelo uso normal. A fatura de uso normal seria entre ou igual a $49,36 e $86,32. Quantos hcf ele poderá usar se quiser que seu uso permaneça na faixa normal?

    Resposta

    O proprietário pode usar o\(16–40\) hcf e ainda se enquadrar na faixa de cobrança de “uso normal”.

    Acesse esse recurso on-line para obter instruções e práticas adicionais sobre como resolver desigualdades compostas.

    • Desigualdades compostas

    Conceitos chave

    • Como resolver uma desigualdade composta com “e”
      1. Resolva cada desigualdade.
      2. Faça um gráfico de cada solução. Em seguida, faça um gráfico dos números que tornam as duas desigualdades verdadeiras. Este gráfico mostra a solução para a desigualdade composta.
      3. Escreva a solução em notação de intervalo.
    • Desigualdade dupla
      • Uma desigualdade dupla é uma desigualdade composta, como\(a<x<b\). É equivalente a\(a<x\) e\(x<b.\)

        Outras formas:\ [\ begin {align*} a<x<b & &\ text {é equivalente a} & & a<x\;\ text {e}\; x<b\\
        a≤x≤b & &\ text {é equivalente a} & & a≤x\;\ text {e}\; x≤b\ \
        a>x>b & &\ text {é equivalente a} & & a>x\;\ text {e}\; x>b\\
        a≥x≥b & &\ text {é equivalente a} & & a≥x\;\ text {e}\; x≥b\ end {align*}\]
    • Como resolver uma desigualdade composta com “ou”
      1. Resolva cada desigualdade.
      2. Faça um gráfico de cada solução. Em seguida, faça um gráfico dos números que tornam qualquer desigualdade verdadeira.
      3. Escreva a solução em notação de intervalo.

    Glossário

    desigualdade composta
    Uma desigualdade composta é composta por duas desigualdades conectadas pela palavra “e” ou pela palavra “ou”.