Skip to main content
Global

2.6: Resolver desigualdades lineares

  1. Last updated
  2. Save as PDF
  • Page ID
    183643

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Representar graficamente desigualdades na reta numérica
    • Resolva desigualdades lineares
    • Transforme palavras em uma desigualdade e resolva
    • Resolva aplicativos com desigualdades lineares

    Antes de começar, faça este teste de prontidão.

    1. Traduzir da álgebra para o inglês:\(15>x\).
      Se você perdeu esse problema, revise [link].
    2. Traduza para uma expressão algébrica:\(15\) é menor que\(x\).
      Se você perdeu esse problema, revise [link].

    Gráfico de desigualdades na reta numérica

    Qual número tornaria a desigualdade\(x>3\) verdadeira? Você está pensando, “\(x\)poderia ser quatro”? Isso está correto, mas\(x\) pode ser 6, também, ou 37, ou até 3.001. Qualquer número maior que três é uma solução para a desigualdade\(x>3\). Mostramos todas as soluções para a desigualdade\(x>3\) na reta numérica sombreando todos os números à direita de três, para mostrar que todos os números maiores que três são soluções. Como o número três em si não é uma solução, colocamos um parêntese aberto em três.

    Também podemos representar desigualdades usando a notação de intervalo. Não há limite para a solução dessa desigualdade. Na notação de intervalo, expressamos\(x>3\) como\((3,\infty)\). O símbolo\(\infty\) é lido como “infinito”. Não é um número real. A figura\(\PageIndex{1}\) mostra a linha numérica e a notação do intervalo.

    A figura mostra a desigualdade, x é maior que 3, representada graficamente em uma reta numérica de menos 5 a 5. Há um sombreamento que começa em 3 e se estende até os números à direita. A solução para a desigualdade é escrita em notação de intervalo. É o intervalo de 3 ao infinito, não incluindo 3.
    Figura\(\PageIndex{1}\): A desigualdade\(x>3\) é representada graficamente nessa reta numérica e escrita em notação de intervalo.

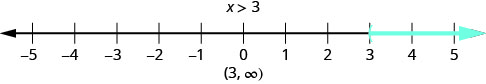
    Usamos o símbolo do parêntese esquerdo, (, para mostrar que o ponto final da desigualdade não está incluído. O símbolo do colchete esquerdo, [, mostra que a extremidade está incluída.

    A desigualdade\(x\leq 1\) significa todos os números menores ou iguais a um. Aqui, precisamos mostrar que uma também é uma solução. Fazemos isso colocando um colchete em\(x=1\). Em seguida, sombreamos todos os números à esquerda de um, para mostrar que todos os números menores que um são soluções (Figura\(\PageIndex{2}\)). Não há limite inferior para esses números. Escrevemos\(x\leq 1x\leq 1 \) em notação de intervalo como\((−\infty,1]\). O símbolo\(−\infty\) é lido como “infinito negativo”.

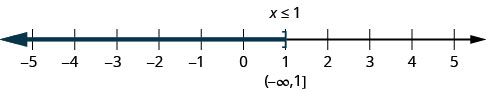
    A figura mostra a desigualdade, x é menor ou igual a l, representada graficamente em uma reta numérica de menos 5 a 5. Há um sombreamento que começa em 1 e se estende até os números à sua esquerda. A solução para a desigualdade é escrita em notação de intervalo. É o intervalo do infinito negativo a um, incluindo 1.
    Figura\(\PageIndex{2}\): A desigualdade\(x\leq 1\) é representada graficamente nessa reta numérica e escrita em notação de intervalo.

    A figura\(\PageIndex{3}\) mostra a linha numérica e a notação de intervalo.

    DESIGUALDADES, LINHAS NUMÉRICAS E NOTAÇÃO INTERVALAR

    A figura mostra que a solução da desigualdade x é maior que a é indicada em uma reta numérica com um parêntese esquerdo em a e sombreado à direita, e que a solução na notação de intervalo é o intervalo de a ao infinito entre parênteses. Mostra que a solução da desigualdade x é maior ou igual a a é indicada em uma reta numérica com um colchete esquerdo em a e sombreado à direita, e que a solução na notação de intervalo é o intervalo a até o infinito dentro de um colchete esquerdo e parêntese direito. Isso mostra que a solução da desigualdade x é menor que a é indicada em uma reta numérica com um parêntese direito em a e sombreado à esquerda, e que a solução na notação de intervalo é o intervalo negativo infinito a a dentro dos parênteses. Isso mostra que a solução da desigualdade x é menor ou igual a a é indicada em uma linha numérica com um colchete direito em a e sombreado à esquerda, e que a solução na notação de intervalo é infinito negativo a a dentro de um parêntese esquerdo e colchete direito.

    A notação para desigualdades em uma reta numérica e em notação de intervalo usa os mesmos símbolos para expressar os pontos finais dos intervalos.

    Exemplo\(\PageIndex{1}\)

    Faça um gráfico de cada desigualdade na reta numérica e escreva em notação de intervalo.

    1. \(x\geq −3\)
    2. \(x<2.5\)
    3. \(x\leq −\frac{3}{5}\)
    Responda

    ⓐ

      \( x \geq -3 \)
    Sombreie à\(−3\) direita e coloque um suporte em\(−3\). .
    Escreva em notação de intervalo. \( [-3, \infty) \)

    ⓑ

      \( x < 2.5 \)
    Sombreie à esquerda de 2,5 e coloque um parêntese em 2,5. .
    Escreva em notação de intervalo. \( (-\infty, 2.5) \)

    ⓒ

      \( x \leq -\dfrac{3}{5} \)
    Sombreie à\(−\frac{3}{5}\) esquerda e coloque um suporte em\(−\frac{3}{5}\). .
    Escreva em notação de intervalo. \( \bigg( -\infty, \dfrac{3}{5}\bigg] \)
     

    Faça um gráfico de cada desigualdade na reta numérica e escreva em notação de intervalo:

    1. \(x>2\)
    2. \(x\leq −1.5\)
    3. \(x\geq \frac{3}{4}\).
    Responda

    ⓐ

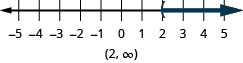
    O gráfico da desigualdade x é maior que 2 é indicado em uma reta numérica com um parêntese esquerdo em 2 e sombreado à direita. A solução na notação de intervalo é o intervalo de 2 ao infinito entre parênteses.

    ⓑ

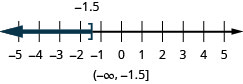
    O gráfico da desigualdade x é menor ou igual a menos 1,5 é indicado em uma reta numérica com um colchete direito em menos 1,5 e sombreado à esquerda. A solução na notação de intervalo é o intervalo do infinito negativo a menos 1,5, entre parênteses esquerdo e colchete direito.

    ⓒ

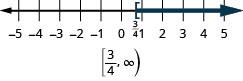
    O gráfico da desigualdade x é maior ou igual a três quartos é indicado em uma reta numérica com um colchete esquerdo em três quartos e sombreado à direita. A solução na notação de intervalo é o intervalo de três quartos ao infinito entre um colchete esquerdo e parênteses esquerdos.

    Exemplo\(\PageIndex{3}\)

    Faça um gráfico de cada desigualdade na reta numérica e escreva em notação de intervalo:

    1. \(x\leq −4\)
    2. \(x\geq 0.5\)
    3. \(x<−\frac{2}{3}\).
    Responda

    ⓐ

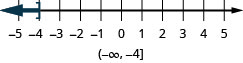
    O gráfico da desigualdade x é menor ou igual a menos 4 é indicado em uma reta numérica com um colchete direito em menos 4 e sombreado à esquerda. A solução na notação de intervalo é o intervalo do infinito negativo a menos 4 entre um parêntese esquerdo e um colchete direito.

    ⓑ

    O gráfico da desigualdade x é maior ou igual a 0,5 é indicado em uma linha numérica com um colchete esquerdo em 0,5 e sombreado à direita. A solução na notação de intervalo é o intervalo de 0,5 ao infinito entre um colchete esquerdo e um parêntese direito.

    ⓒ

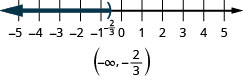
    O gráfico da desigualdade x é menor que menos dois terços é indicado em uma reta numérica com um parêntese direito em menos dois terços e sombreado à esquerda. A solução na notação de intervalo é o intervalo do infinito negativo a menos dois terços entre parênteses.

    Quais números são maiores que dois, mas menores que cinco? Você está pensando, digamos,\(2.5,\space 3,\space 3\frac{2}{3},\space 4,\space 4,\space 99\)? Podemos representar todos os números entre dois e cinco com a desigualdade\(2<x<5\). Podemos mostrar\(2<x<5\) na reta numérica sombreando todos os números entre dois e cinco. Novamente, usamos os parênteses para mostrar que os números dois e cinco não estão incluídos. Veja a Figura.

    O gráfico da desigualdade 2 é menor que x, que é menor que 5, mostra os círculos abertos a 2 e 5 e sombreamento entre eles.
    Figura\(\PageIndex{3}\)
     

    Faça um gráfico de cada desigualdade na reta numérica e escreva em notação de intervalo.

    ⓐ\(−3<x<4\) ⓑ\(−6\leq x<−1\) ⓒ\(0\leq x\leq 2.5\)

    Responda

    ⓐ

        \(-3 < x < 4\)
    Sombra entre\(−3\) 0 e 4.
    Coloque parênteses em\(−3\) e 4.    		   .
    Escreva em notação de intervalo.   \( (-3,4) \)

    ⓑ

          \( -6 \leq x < -1 \)
    Sombra entre\(−6\) e −1.
    Coloque um colchete em\(−6\) e
    um parêntese em −1.    		     .
    Escreva em notação de intervalo.     \( [-6,1) \)

    ⓒ

          \( 0 \leq x \leq 2.5 \)
    Sombra entre 0 e 2,5.
    Coloque um colchete em 0 e em 2,5.    		     .
    Escreva em notação de intervalo.     \( [0, 2.5] \)
    Exemplo\(\PageIndex{5}\)

    Faça um gráfico de cada desigualdade na reta numérica e escreva em notação de intervalo:

    ⓐ\(−2<x<1\) ⓑ\(−5\leq x<−4\) ⓒ\(1\leq x\leq 4.25\)

    Responda

    ⓐ

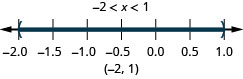
    Menos 2 é menos x, que é menor que 1. Existem círculos abertos em menos 2 e 1 e sombreados entre menos 2 e 1 na reta numérica. Coloque parênteses em menos 2 e 1. Escreva em notação de intervalo.

    ⓑ

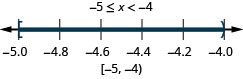
    Menos 5 é menor ou igual a x, que é menor que menos 4. Há um círculo fechado em menos 6 e um círculo aberto em menos 4 e sombreado entre menos 5 e menos 4 na reta numérica. Coloque um colchete em menos 5 e um parêntese em menos 4. Escreva em notação de intervalo.

    ⓒ

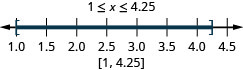
    1 é menor ou igual a x, que é menor que 4,25. Há um círculo fechado em 1 e um círculo fechado em 4,25 e sombreado entre 1 e 4,25 na reta numérica. Coloque os colchetes em 1 e 4,25. Escreva em notação de intervalo.

    Exemplo\(\PageIndex{6}\)

    Faça um gráfico de cada desigualdade na reta numérica e escreva em notação de intervalo:

    ⓐ\(−6<x<2\) ⓑ\(−3\leq x< −1\) ⓒ\(2.5\leq x\leq 6\)

    Responda

    ⓐ

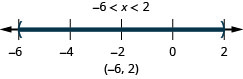
    Menos 6 é menor que x, que é menor que 2. Há um círculo aberto em menos 6 e um círculo aberto em 2 e sombreado entre menos 6 e 2 na reta numérica. Coloque parênteses em menos 6 e 2. Escreva em notação de intervalo.

    ⓑ

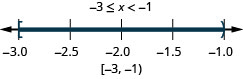
    Menos 3 é menor ou igual a x, que é menor que menos 1. Há um círculo fechado em menos 3 e um círculo aberto em menos 1 e sombreado entre menos 3 e menos 1 na reta numérica. Coloque um colchete em menos 3 e um parêntese em menos 1. Escreva em notação de intervalo.

    ⓒ

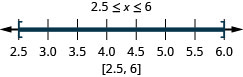
    2,5 é menor ou igual a x, que é menor ou igual a 6. Há um círculo fechado em 2,5 e um círculo fechado em 6 e sombreado entre 2,5 e 6 na reta numérica. Coloque os colchetes em 2,5 e 6. Escreva em notação de intervalo.

    Resolver desigualdades lineares

    Uma desigualdade linear é muito parecida com uma equação linear, mas o sinal de igual é substituído por um sinal de desigualdade. Uma desigualdade linear é uma desigualdade em uma variável que pode ser escrita em uma das formas\(ax+b<c\),\(ax+b\leq c\),\(ax+b>c\), ou\(ax+b\geq c\).

    DESEQUAÇÃO LINEAR

    Uma desigualdade linear é uma desigualdade em uma variável que pode ser escrita em uma das seguintes formas, onde\(a, \, b,\) e\(c\) são números reais e\(a≠0\):

    \[ \begin{array} {llll} {ax+b<c,} &{ax+b\leq c,} &{ax+b>c,} &{ax+b\geq c.} \\ \nonumber \end{array}\]

    Quando resolvemos equações lineares, pudemos usar as propriedades da igualdade para somar, subtrair, multiplicar ou dividir os dois lados e ainda manter a igualdade. Propriedades similares são válidas para desigualdades.

    Podemos somar ou subtrair a mesma quantidade de ambos os lados de uma desigualdade e ainda manter a desigualdade. Por exemplo:

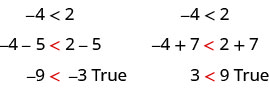
    Menos 4 é menor que 2. Menos 4 menos 5 é menor que 2 menos 5. Menos 9 é menor que menos 3, o que é verdade. Menos 4 é menor que 2. Menos 4 mais 7 é menor que 2 mais 7. 3 é menor que 9, o que é verdade.

    Observe que o sinal de desigualdade permaneceu o mesmo.

    Isso nos leva às propriedades de adição e subtração da desigualdade.

    PROPRIEDADE DE ADIÇÃO E SUBTRAÇÃO DA DESIGUALDADE

    Para qualquer número\(a, \, b,\) e\(c,\) se\(a<b\), então

    \[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \nonumber \end{array}\]

    Podemos somar ou subtrair a mesma quantidade de ambos os lados de uma desigualdade e ainda manter a desigualdade.

    O que acontece com uma desigualdade quando dividimos ou multiplicamos os dois lados por uma constante?

    Vamos primeiro multiplicar e dividir os dois lados por um número positivo.

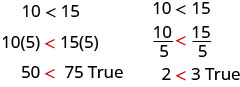
    10 é menor que 15. 10 vezes 5 é menor que 15 vezes 5. 50 é menor que 75 é verdadeiro. 10 é menor que 15. 10 dividido por 5 é menor que 15 dividido por 5. 2 é menor que 3 é verdadeiro.

    Os sinais de desigualdade permaneceram os mesmos.

    A desigualdade permanece a mesma quando dividimos ou multiplicamos por um número negativo?

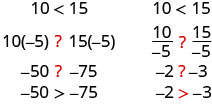
    10 é menor que 15 10 vezes menos 5 está em branco 15 vezes menos 5? Menos 50 é menos 75 em branco. Menos 50 é maior que menos 75. 10 é menor que 15. 10 dividido por menos 5 é branco 15 dividido por menos 5. Menos 2 está em branco, menos 3. Menos 2 está em branco, menos 3.

    Observe que quando preenchemos os sinais de desigualdade, os sinais de desigualdade inverteram sua direção.

    Quando dividimos ou multiplicamos uma desigualdade por um número positivo, o sinal de desigualdade permanece o mesmo. Quando dividimos ou multiplicamos uma desigualdade por um número negativo, o sinal de desigualdade se inverte.

    Isso nos dá a propriedade de multiplicação e divisão da desigualdade.

    PROPRIEDADE DE MULTIPLICAÇÃO E DIVISÃO DA DESIGUAL

    Para qualquer número\(a, \, b,\) e\(c,\)

    \[\begin{array} {l} {\text{multiply or divide by a positive}} \\ \\ \space\space\space\space\text{if }a<b\text{ and }c>0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\text{if }a>b\text{ and }c>0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}. \\ \\ \text{ multiply or divide by a negative } \\ \\ \space\space\space\space\text{if }a<b\text{ and }c<0\text{, then }ac>bc \text{ and }\frac{a}{c}>\frac{b}{c}.\\ \space\space\space\space\text{if }a>b\text{ and }c<0\text{, then }ac<bc \text{ and }\frac{a}{c}<\frac{b}{c}.\\ \nonumber \end{array}\]

    Quando dividimos ou multiplicamos uma desigualdade por\(a\):

    • número positivo, a desigualdade permanece a mesma.
    • número negativo, a desigualdade se inverte.

    Às vezes, ao resolver uma desigualdade, como no exemplo a seguir, a variável termina à direita. Podemos reescrever a desigualdade ao contrário para colocar a variável à esquerda.

    \[x>a \text{ has the same meaning as } a<x \nonumber \]

    Pense nisso como “Se Xander é mais alto que Andy, então Andy é mais baixo que Xander”.

    Exemplo\(\PageIndex{7}\)

    Resolva cada desigualdade. Faça um gráfico da solução na reta numérica e escreva a solução em notação de intervalo.

    ⓐ\(x−\frac{3}{8}\leq \frac{3}{4}\) ⓑ\(9y<54\) ⓒ\(−15<\frac{3}{5}z\)

    Responda

    ⓐ

      .
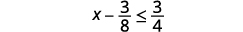
    Adicione 3838 aos dois lados da desigualdade. .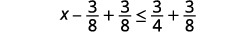
    Simplifique. .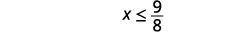
    Faça um gráfico da solução na reta numérica. .
    Escreva a solução em notação de intervalo. .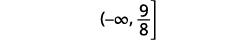

    ⓑ

      .
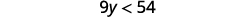
    Divida os dois lados da desigualdade por 9; como
    9 é positivo, a desigualdade permanece a mesma.    		 .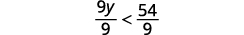
    Simplifique. .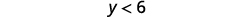
    Faça um gráfico da solução na reta numérica. .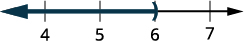
    Escreva a solução em notação de intervalo. .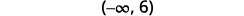

    ⓒ

      .

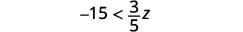
    Multiplique os dois lados da desigualdade por\(\frac{5}{3}\).
    Como\(\frac{5}{3}\) é positivo, a desigualdade permanece a mesma.

    		 .
    Simplifique. .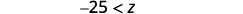
    Reescreva com a variável à esquerda. .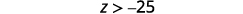
    Faça um gráfico da solução na reta numérica. .
    Escreva a solução em notação de intervalo. .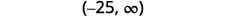
     

    Resolva cada desigualdade, represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo:

    ⓐ\(p−\frac{3}{4}\geq \frac{1}{6}\) ⓑ\(9c>72\) ⓒ\(24\leq \frac{3}{8}m\)

    Responda

    ⓐ

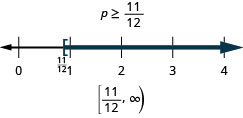
    p é menor que onze duodécimos. A solução na reta numérica tem um colchete direito em onze duodécimos com sombreamento à direita. A solução na notação de intervalo é, onze duodécimos até o infinito dentro de um colchete e parêntese.

    ⓑ

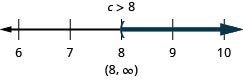
    c é menor que 8. A solução na reta numérica tem um colchete esquerdo em 8 com sombreamento à direita. A solução na notação de intervalo é de 8 até o infinito entre parênteses.

    ⓒ

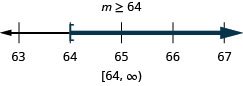
    m é maior ou igual a 8. A solução na reta numérica tem um colchete direito em 64 com sombreamento à direita. A solução na notação de intervalo é 64 até o infinito dentro de um colchete e parênteses.

    Exemplo\(\PageIndex{9}\)

    Resolva cada desigualdade, represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo:

    ⓐ\(r−\frac{1}{3}\leq \frac{7}{12}\) ⓑ\(12d\leq 60\) ⓒ\(−24<\frac{4}{3}n\)

    Responda

    ⓐ

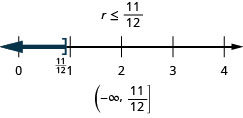
    r é menor ou igual a onze duodécimos. A solução na reta numérica tem um colchete esquerdo em onze duodécimos com sombreamento à esquerda. A solução na notação de intervalo é de menos infinito a onze duodécimos dentro de um parêntese e um colchete.

    ⓑ

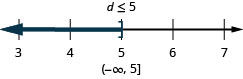
    c é menor ou igual a 5. A solução na linha numérica tem um colchete direito em 5 com sombreamento à esquerda. A solução na notação de intervalo é menos infinito a 5 entre parênteses e colchetes.

    ⓒ

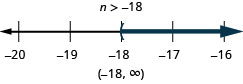
    n é maior que menos 18. A solução na reta numérica tem um parêntese esquerdo em menos 18 com sombreamento à direita. A solução na notação de intervalo é de menos 18 a infinito entre parênteses.

    Tenha cuidado ao multiplicar ou dividir por um número negativo — lembre-se de reverter o sinal de desigualdade.

    Exemplo\(\PageIndex{10}\)

    Resolva cada desigualdade, represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo.

    ⓐ\(−\frac{1}{3}m\geq \frac{6}{5}\) ⓑ\(\frac{n}{−2} \geq 8\)

    Responda

    ⓐ

      .
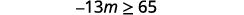
    Divida os dois lados da desigualdade por\(−\frac{1}{3}\).
    Como\(−\frac{1}{3}\) é negativo, a desigualdade se inverte.    		 .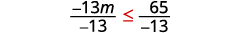
    Simplifique. .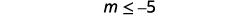
    Faça um gráfico da solução na reta numérica. .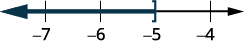
    Escreva a solução em notação de intervalo. .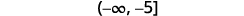

    ⓑ

      .
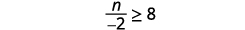
    Multiplique os dois lados da desigualdade por\(−2\).
    Como\(−2\) é negativo, a desigualdade se inverte.    		 .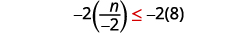
    Simplifique. .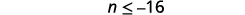
    Faça um gráfico da solução na reta numérica. .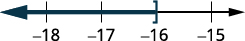
    Escreva a solução em notação de intervalo. .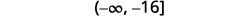
    Exemplo\(\PageIndex{11}\)

    Resolva cada desigualdade, represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo:

    ⓐ\(−8q<32\) ⓑ\(\frac{k}{−12} \leq 15\).

    Responda

    ⓐ

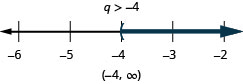
    q é maior ou igual a menos 4. A solução na reta numérica tem um parêntese esquerdo em menos 4 com sombreamento à direita. A solução na notação de intervalo é de menos 4 ao infinito entre parênteses.

    ⓑ

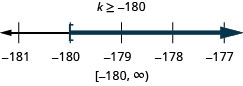
    k é maior ou igual a menos 180. A solução na reta numérica tem um colchete esquerdo em menos 180 com sombreamento à direita. A solução na notação de intervalo é de menos 180 ao infinito dentro de um colchete e um parêntese.

    Exemplo\(\PageIndex{12}\)

    Resolva cada desigualdade, represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo:

    ⓐ\(−7r\leq −70\) ⓑ\(\frac{u}{−4}\geq −16\).

    Responda

    ⓐ

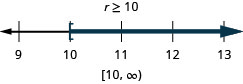
    r é maior ou igual a 10. A solução na reta numérica tem um colchete esquerdo em 10 com sombreamento à direita. A solução na notação de intervalo é de 10 até o infinito dentro de um colchete e parêntese.

    ⓑ

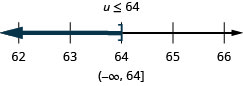
    u é menor ou igual a 64. A solução na reta numérica tem um colchete direito em 64 com sombreamento à esquerda. A solução na notação de intervalo é menos infinito até 64 entre parênteses e um colchete.

    A maioria das desigualdades exigirá mais de um passo para ser resolvida. Seguimos os mesmos passos que usamos na estratégia geral para resolver equações lineares, mas preste muita atenção ao multiplicar ou dividir para isolar a variável.

     

    Resolva a desigualdade\(6y\leq 11y+17\), represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo.

    Responda
      .
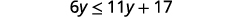
    Subtraia 11y11y de ambos os lados para coletar
    as variáveis à esquerda.    		 .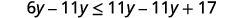
    Simplifique. .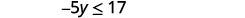
    Divida os dois lados da desigualdade por −5, −5
    e inverta a desigualdade.    		 .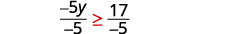
    Simplifique. .
    Faça um gráfico da solução na reta numérica. .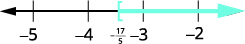
    Escreva a solução em notação de intervalo. .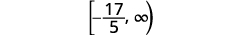
     

    Resolva a desigualdade, represente graficamente a solução na reta numérica e escreva a solução na notação de intervalo:\(3q\geq 7q−23\).

    Responda

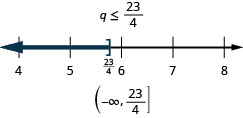
    q é menor ou igual a 23 dividido por 4. A solução na reta numérica tem um colchete direito em 23 dividido por 4 com sombreamento à esquerda. A solução na notação de intervalo é o infinito negativo a 23 dividido por 4 dentro de um parêntese e um colchete.

    Exemplo\(\PageIndex{15}\)

    Resolva a desigualdade, represente graficamente a solução na reta numérica e escreva a solução na notação de intervalo:\(6x<10x+19\).

    Responda

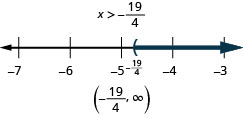
    x é maior que menos 19 dividido por 4. A solução na reta numérica tem um parêntese esquerdo em menos 19 dividido por 4 com sombreamento à direita. A solução na notação de intervalo é menos 19 dividido por 4 até o infinito entre parênteses.

    Ao resolver desigualdades, geralmente é mais fácil coletar as variáveis no lado em que o coeficiente da variável é maior. Isso elimina coeficientes negativos e, portanto, não precisamos multiplicar ou dividir por um negativo, o que significa que não precisamos nos lembrar de reverter o sinal de desigualdade.

    Exemplo\(\PageIndex{16}\)

    Resolva a desigualdade\(8p+3(p−12)>7p−28\), represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo.

    Responda
      \(8p+3(p−12)>7p−28\)
    Simplifique cada lado o máximo possível.  
    Distribuir. \(8p+3p−36>7p−28\)
    Combine termos semelhantes. \(11p−36>7p−28\)
    Subtraia\(7p\) de ambos os lados para coletar as
    variáveis à esquerda, desde\(11>7\).    		 \(11p−36−7p>7p−28−7p\)
    Simplifique. \(4p−36>−28\)
    Adicione\(36\) aos dois lados para coletar as
    constantes à direita.    		 \(4p−36+36>−28+36\)
    Simplifique. \(4p>8\)
    Divida os dois lados da desigualdade por
    \(4\); a desigualdade permanece a mesma.    		 \(\dfrac{4p}{4}>\dfrac{8}{4}\)
    Simplifique. \(p>2\)
    Faça um gráfico da solução na reta numérica. .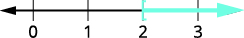
    Escreva a solução em notação de intervalo. \((2,\infty)\)
    Exemplo\(\PageIndex{17}\)

    Resolva a desigualdade\(9y+2(y+6)>5y−24\), represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo.

    Responda

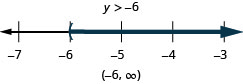
    y é maior que menos 6. A solução na reta numérica tem um parêntese esquerdo em menos 6 com sombreamento à direita. A solução na notação de intervalo é de menos 6 ao infinito entre parênteses.

    Exemplo\(\PageIndex{18}\)

    Resolva a desigualdade\(6u+8(u−1)>10u+32\), represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo.

    Responda

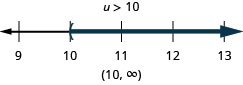
    u é maior que menos 10. A solução na reta numérica tem um parêntese esquerdo em 10 com sombreamento à direita. A solução na notação de intervalo é de 10 até o infinito entre parênteses.

    Assim como algumas equações são identidades e outras contradições, as desigualdades também podem ser identidades ou contradições. Reconhecemos essas formas quando ficamos apenas com constantes à medida que resolvemos a desigualdade. Se o resultado for uma afirmação verdadeira, temos uma identidade. Se o resultado for uma declaração falsa, temos uma contradição.

    Exemplo\(\PageIndex{19}\)

    Resolva a desigualdade\(8x−2(5−x)<4(x+9)+6x\), represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo.

    Responda
    Simplifique cada lado o máximo possível.   \(8x−2(5−x)<4(x+9)+6x\)
    Distribuir.   \(8x−10+2x<4x+36+6x\)
    Combine termos semelhantes.   \(10x−10<10x+36\)
    Subtraia\({\color{red}{10x}}\) dos dois lados para coletar as variáveis à esquerda.   \(10x−10\,{\color{red}{-\,10x}}<10x+36\,{\color{red}{-\,10x}}\)
    Simplifique.   \(−10<36\)
    Os desapareceram e temos uma
    afirmação verdadeira.\(x\)    		   A desigualdade é uma identidade.
    A solução são todos números reais.
    Faça um gráfico da solução na reta numérica.   .
    Escreva a solução em notação de intervalo.   \((−\infty,\infty)\)
    Exemplo\(\PageIndex{20}\)

    Resolva a desigualdade\(4b−3(3−b)>5(b−6)+2b\), represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo.

    Responda

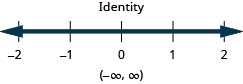
    A desigualdade é uma identidade. Sua solução na reta numérica é sombreada para todos os valores. A solução na notação de intervalo é de menos infinito a infinito entre parênteses.

    Exemplo\(\PageIndex{21}\)

    Resolva a desigualdade\(9h−7(2−h)<8(h+11)+8h\), represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo.

    Responda

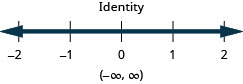
    A desigualdade é uma identidade. Sua solução na reta numérica é sombreada para todos os valores. A solução na notação de intervalo é de menos infinito a infinito entre parênteses.

    Podemos eliminar frações nas desigualdades da mesma forma que fizemos nas equações. Novamente, tenha cuidado com os sinais ao multiplicar ou dividir por um negativo.

    Exemplo\(\PageIndex{22}\)

    Resolva a desigualdade\(\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}\), represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo.

    Responda
      \(\frac{1}{3}a−\frac{1}{8}a>\frac{5}{24}a+\frac{3}{4}\)
    Multiplique os dois lados pelo LCD, 24,
    para limpar as frações.    		 \({\color{red}{24}}\left(\dfrac{1}{3}a−\dfrac{1}{8}a\right)>\,{\color{red}{24}}\left(\dfrac{5}{24}a+\dfrac{3}{4}\right)\)
    Simplifique. \( 8a - 3a > 5a + 18 \)
    Combine termos semelhantes. \( 5a > 5a + 18\)
    Subtraia\(5a\) dos dois lados para coletar as
    variáveis à esquerda.    		 \( 5a \,{\color{red}{-\,5a}} > 5a \,{\color{red}{-\,5a}} + 18\)
    Simplifique. \(0 > 18 \)
    A afirmação é falsa. A desigualdade é uma contradição.
    Não há solução.
    Faça um gráfico da solução na reta numérica. .
    Escreva a solução em notação de intervalo. Não há solução.
    Exemplo\(\PageIndex{23}\)

    Resolva a desigualdade\(\frac{1}{4}x−\frac{1}{12}x>\frac{1}{6}x+\frac{7}{8}\), represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo.

    Responda

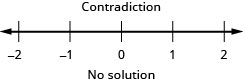
    A desigualdade é uma contradição. Então, não há solução. Como resultado, não há gráfico na linha numérica ou na notação do intervalo.

    Exemplo\(\PageIndex{24}\)

    Resolva a desigualdade\(\frac{2}{5}z−\frac{1}{3}z<\frac{1}{15}z−\frac{3}{5}\), represente graficamente a solução na reta numérica e escreva a solução em notação de intervalo.

    Responda

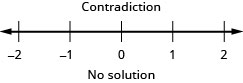
    A desigualdade é uma contradição. Então, não há solução. Como resultado, não há gráfico na linha numérica ou na notação do intervalo.

    Traduza para uma desigualdade e resolva

    Para traduzir frases em inglês em desigualdades, precisamos reconhecer as frases que indicam a desigualdade. Algumas palavras são fáceis, como “mais que” e “menos que”. Mas outros não são tão óbvios. A tabela mostra algumas frases comuns que indicam desigualdades.

    \(>\) \(\geq\) \(<\) \(\leq\)
    \ (>\) ">\)” data-valign="middle” class="lt-math-17389">é maior do

    que

    é maior do que

    excede    		 \ (\ geq\)” data-valign="middle">é maior ou igual a

    é pelo menos não

    é menor que

    o mínimo    		 \ (é <\)” data-valign="middle"> menor que é

    menor do que tem

    menos do que é

    menor que    		 \ (\ leq\)” data-valign="middle">é menor ou igual a

    é no máximo não



    é mais do que o máximo
    Exemplo\(\PageIndex{25}\)

    Traduza e resolva. Em seguida, faça um gráfico da solução na reta numérica e escreva a solução em notação de intervalo.

    \[\text{Twenty-seven less than }x\text{ is at least }48.\nonumber\]

    Resposta
      .
    Traduzir. \(x - 27 \geq 48\)
    Resolver — adicione 27 aos dois lados. \( x - 27 \, {\color{red}{+\, 27}} \geq 48 \, {\color{red}{+\, 27}}\)
    Simplifique. \(x \geq 75\)
    Gráfico na reta numérica. .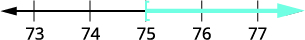
    Escreva em notação de intervalo. \([75, \infty)\)
     

    Traduza e resolva. Em seguida, faça um gráfico da solução na reta numérica e escreva a solução em notação de intervalo.

    \[\text{Nineteen less than } p \text{ is no less than }47.\nonumber\]

    Resposta

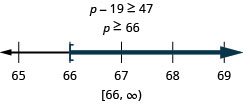
    p menos 19 é maior ou igual a 47. Sua solução é p maior ou igual a 66. A solução na reta numérica tem um colchete esquerdo em 66 com sombreamento à direita. A solução na notação de intervalo é 66 até o infinito dentro de um colchete e um parêntese.

    Exemplo\(\PageIndex{27}\)

    Traduza e resolva. Em seguida, faça um gráfico da solução na reta numérica e escreva a solução em notação de intervalo.

    \[\text{Four more than }a\text{ is at most }15.\nonumber\]

    Resposta

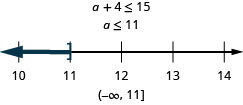
    a mais 4 é menor ou igual a 15. Sua solução é a é menor ou igual a 11. A solução na reta numérica tem um colchete direito em 11 com sombreamento à esquerda. A solução na notação de intervalo é menos infinito até 11 dentro de um parêntese e colchete.

    Resolva aplicativos com desigualdades lineares

    Muitas situações da vida real exigem que resolvamos as desigualdades. O método que usaremos para resolver aplicações com desigualdades lineares é muito parecido com o que usamos quando resolvemos aplicações com equações.

    Vamos ler o problema e garantir que todas as palavras sejam compreendidas. Em seguida, identificaremos o que estamos procurando e atribuiremos uma variável para representá-lo. Vamos reafirmar o problema em uma frase para facilitar a tradução em uma desigualdade. Então, resolveremos a desigualdade.

    Às vezes, um aplicativo exige que a solução seja um número inteiro, mas a solução algébrica para a desigualdade não é um número inteiro. Nesse caso, devemos arredondar a solução algébrica para um número inteiro. O contexto da aplicação determinará se arredondamos para cima ou para baixo.

    Exemplo\(\PageIndex{28}\)

    Dawn ganhou uma mini-bolsa de $4.000 para comprar computadores tablet para sua sala de aula. Os tablets que ela gostaria de comprar custam $254,12 cada, incluindo impostos e entrega. Qual é o número máximo de tablets que a Dawn pode comprar?

    Resposta

    \(\begin{array} {ll} {\textbf{Step 1. Read }\text{ the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the maximum number of tablets Dawn can buy}} \\ {\textbf{Step 3. Name}\text{ what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }n= \text{ the number of tablets.}} \\ {\text{Choose a variable to represent that}} &{} \\{\text{quantity.}} &{} \\ {\textbf{Step 4. Translate.}\text{Write a sentence that gives the}} &{} \\ {\text{information to find it.}} &{$254.12\text{ times the number of tablets is}} \\ {} &{\text{no more than }$4,000.} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space 254.12n\leq 4000} \\ {\text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15.74} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space n\leq 15} \\{\text{But }n\text{ must be a whole number of}} &{} \\ {\text{tablets, so round to }15.} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{Rounding down the price to } $250, 15} &{} \\ {\space\space\space \text{tablets would cost }$3,750,\text{ while } 16} &{} \\ {\space\space\space \text{tablets would be }$4,000.\text{So a}} &{} \\ {\space\space\space \text{maximum of 15 tablets at }$254.12} &{} \\ {\space\space\space \text{seems reasonable.}} &{} \\ {\textbf{Step 7. Answer }\text{the question with a complete sentence.}} &{\text{Dawn can buy a maximum of 15 tablets.}} \\ \end{array}\)

    Exemplo\(\PageIndex{29}\)

    Angie tem $20 para gastar em caixas de suco para o piquenique pré-escolar de seu filho. Cada pacote de caixas de suco custa $2,63. Qual é o número máximo de pacotes que ela pode comprar?

    Resposta

    Angie pode comprar 7 pacotes de suco.

    Exemplo\(\PageIndex{30}\)

    Daniel quer surpreender a namorada com uma festa de aniversário no restaurante favorito dela. O jantar custará $42,75 por pessoa, incluindo gorjeta e impostos. Seu orçamento para a festa é de $500. Qual é o número máximo de pessoas que Daniel pode ter na festa?

    Resposta

    Daniel pode ter 11 pessoas na festa.

    Exemplo\(\PageIndex{31}\)

    O plano telefônico de Taleisha custa a ela $28,80 por mês mais $0,20 por mensagem de texto. Quantas mensagens de texto ela pode enviar/receber e manter sua conta telefônica mensal de no máximo $50?

    Resposta

    \(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of text messages Taleisha can make}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }t= \text{the number of text messages.}} \\ {\text{Choose a variable to represent that}} &{} \\ {\text{quantity.}} &{} \\ {\textbf{Step 4. Translate }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$28.80\text{ plus }$0.20\text{ times the number of}} \\ {} &{\text{text messages is less than or equal to }$50.} \\ {} &{28.80+0.20t \leq 50} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 0.2t\leq 21.2} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space t\leq 106\text{ text messages}} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\{\space\space\space \text{Yes, }28.80+0.20(106)=50.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{} \\ {} &{\text{Taleisha can send/receive no more than}} \\ {} &{106\text{ text messages to keep her bill no}} \\ {} &{\text{more than } $50.} \\ \end{array}\)

    Exemplo\(\PageIndex{32}\)

    Sergio e Lizeth têm um orçamento de férias muito apertado. Eles planejam alugar um carro de uma empresa que cobra $75 por semana mais $0,25 por milha. Quantas milhas eles podem viajar durante a semana e ainda manter dentro do orçamento de $200?

    Resposta

    Sergio e Lizeth não podem viajar mais do que 500 milhas.

    Exemplo\(\PageIndex{33}\)

    A conta de aquecimento da Rameen é de $5,42 por mês mais $1,08 por termo. Quantas garrafas térmicas Rameen pode usar se quiser que sua conta de aquecimento seja de no máximo $87,50.

    Resposta

    A conta de aquecimento da Rameen é de $5,42 por mês mais $1,08 por termo. Quantas garrafas térmicas Rameen pode usar se quiser que sua conta de aquecimento seja de no máximo $87,50.

    Lucro é o dinheiro que permanece quando os custos são subtraídos da receita. No próximo exemplo, encontraremos o número de trabalhos que uma pequena empresária precisa realizar todos os meses para obter um certo lucro.

    Exemplo\(\PageIndex{34}\)

    Felicity tem um negócio de caligrafia. Ela cobra $2,50 por convite de casamento. Suas despesas mensais são de $650. Quantos convites ela deve escrever para obter um lucro de pelo menos $2.800 por mês?

    Resposta

    \(\begin{array} {ll} {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of invitations Felicity needs to write}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{\text{Let }j=\text{ the number of invitations.}} \\ {} &{} \\ {\space\space\space\text{Choose a variable to represent it.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{$2.50 \text{ times the number of invitations}} \\ {} &{\text{minus }$650\text{ is at least }$2,800.} \\ {} &{\space\space\space 2.50j−650\geq 2,800} \\ {\space\space\space \text{Translate into an inequality.}} &{} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 2.5j\geq 3,450} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space j\geq 1,380 \text{ invitations}} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space \text{If Felicity wrote }1400\text{ invitations, her}} &{} \\ {\space\space\space \text{profit would be }2.50(1400)−650, \text{or}} &{} \\ {\space\space\space $2,850.\text{ This is more than }$2800.} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Felicity must write at least }1,380\text{ invitations.}} \\ \end{array}\)

    Exemplo\(\PageIndex{35}\)

    Caleb tem um negócio de babá de animais de estimação. Ele cobra $32 por hora. Suas despesas mensais são de $2.272. Quantas horas ele deve trabalhar para obter um lucro de pelo menos $800 por mês?

    Resposta

    Caleb deve trabalhar pelo menos 96 horas.

    Exemplo\(\PageIndex{36}\)

    Elliot tem uma empresa de manutenção paisagística. Suas despesas mensais são de $1.100. Se ele cobra $60 por trabalho, quantos empregos ele deve fazer para obter um lucro de pelo menos $4.000 por mês?

    Resposta

    Elliot deve trabalhar pelo menos 85 empregos.

    Há muitas situações em que várias quantidades contribuem para a despesa total. Devemos nos certificar de contabilizar todas as despesas individuais ao resolvermos problemas como esse.

    Exemplo\(\PageIndex{37}\)

    Malik está planejando uma viagem de férias de verão de seis dias. Ele economiza $840 e ganha $45 por hora para dar aulas particulares. A viagem custará a ele $525 para passagem aérea, $780 para comida e passeios turísticos e $95 por noite para o hotel. Quantas horas ele deve ser tutor para ter dinheiro suficiente para pagar a viagem?

    Resposta

    \(\begin{array} {ll} {} &{} \\ {\textbf{Step 1. Read }\text{the problem.}} &{} \\ {\textbf{Step 2. Identify }\text{what you are looking for.}} &{\text{the number of hours Malik must tutor}} \\ {\textbf{Step 3. Name }\text{what you are looking for.}} &{} \\ {} &{} \\ {} &{\text{Let }h=\text{ the number of hours.}} \\ {\space\space\space\space\space\space\space \text{Choose a variable to represent that}} &{} \\ {\space\space\space\space\space\space\space \text{quantity.}} &{} \\ {\textbf{Step 4. Translate. }\text{Write a sentence that}} &{} \\ {\text{gives the information to find it.}} &{} \\ {} &{\text{The expenses must be less than or equal to}} \\{} &{\text{the income. The cost of airfare plus the}} \\{} &{\text{cost of food and sightseeing and the hotel}} \\{} &{\text{bill must be less than the savings plus the}} \\{} &{\text{amount earned tutoring.}} \\{} &{} \\ {} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space \text{Translate into an inequality.}} &{525+780+95(6)\leq 840+45h} \\ {\textbf{Step 5. Solve }\text{the inequality.}} &{} \\ {} &{} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,875\leq 840+45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 1,035\leq 45h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space 23\leq h} \\ {} &{\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space h\geq 23} \\ {} &{} \\ {} &{} \\ {\textbf{Step 6. Check }\text{the answer in the problem}} &{} \\ {\text{and make sure it makes sense.}} &{} \\ {\text{We substitute 23 into the inequality.}} &{} \\ {} &{} \\ {} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45h} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 840+45(23)} &{} \\ {\space\space\space\space\space\space\space\space 1,875\leq 1875} &{} \\ {\textbf{Step 7. Write }\text{a sentence that answers the question.}} &{\text{Malik must tutor at least }23\text{ hours.}} \\ \end{array}\)

    Exemplo\(\PageIndex{38}\)

    A melhor amiga de Brenda está tendo um casamento no destino e o evento durará três dias. Brenda economiza $500 e pode ganhar $15 por hora como babá. Ela espera pagar $350 de passagem aérea, $375 para comida e entretenimento e $60 por noite por sua parte em um quarto de hotel. Quantas horas ela deve ser babá para ter dinheiro suficiente para pagar a viagem?

    Resposta

    Brenda deve ser babá por pelo menos 27 horas.

    Exemplo\(\PageIndex{39}\)

    Josue quer fazer uma viagem de 10 noites com amigos na próxima primavera. Custará a ele $180 para gasolina, $450 para comida e $49 por noite para dividir um quarto de motel. Ele tem $520 em economias e pode ganhar $30 por calçada removendo neve. Quantas calçadas ele deve cavar para ter dinheiro suficiente para pagar a viagem?

    Resposta

    Josue deve cavar pelo menos 20 calçadas.

    Conceitos-chave

    • Desigualdades, retas numéricas e notação de intervalo
      \(x>a \quad x\geq a\quad x<a\quad x\leq a\)
      A figura mostra que a solução da desigualdade x é maior que a é indicada em uma reta numérica com um parêntese esquerdo em a e sombreado à direita, e que a solução na notação de intervalo é o intervalo de a ao infinito entre parênteses. Mostra que a solução da desigualdade x é maior ou igual a a é indicada em uma reta numérica com um colchete esquerdo em a e sombreado à direita, e que a solução na notação de intervalo é o intervalo a até o infinito dentro de um colchete esquerdo e parêntese direito. Isso mostra que a solução da desigualdade x é menor que a é indicada em uma reta numérica com um parêntese direito em a e sombreado à esquerda, e que a solução na notação de intervalo é o intervalo negativo infinito a a dentro dos parênteses. Isso mostra que a solução da desigualdade x é menor ou igual a a é indicada em uma linha numérica com um colchete direito em a e sombreado à esquerda, e que a solução na notação de intervalo é infinito negativo a a dentro de um parêntese esquerdo e colchete direito.
    • Desigualdade linear
      • Uma desigualdade linear é uma desigualdade em uma variável que pode ser escrita em uma das seguintes formas, onde a, b e c são números reais e\(a\neq 0\):

        \[ax+b<c, \qquad ax+b\leq c, \qquad ax+b>c, \qquad ax+b\geq c.\nonumber\]

    • Propriedade de adição e subtração da desigualdade
      • Para qualquer número a, b e c, se a<b, então<b, então

        \[\begin{array} {ll} {a+c<b+c} &{a−c<b−c} \\ {a+c>b+c} &{a−c>b−c} \\ \end{array} \nonumber\]

      • Podemos somar ou subtrair a mesma quantidade de ambos os lados de uma desigualdade e ainda manter a desigualdade.
    • Propriedade de multiplicação e divisão da desigualdade
      • Para qualquer número a, b e c,
        \(\begin{array} {l} \text{multiply or divide by a }\textbf{positive} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c>0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c>0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \text{multiply or divide by a }\textbf{negative} \\ \\ \space\space\space\space\space\space\space\text{if }a<b\text{ and }c<0,\text{ then } ac>bc\text{ and }\frac{a}{c}>\frac{b}{c}. \\ \space\space\space\space\space\space\space\text{if }a>b\text{ and }c<0,\text{ then } ac<bc\text{ and }\frac{a}{c}<\frac{b}{c}. \\ \end{array}\)
    • Frases que indicam desigualdades
      \(>\) \(\geq\) \(<\) \(\leq\)
      \ (>\) ">é maior do

      que

      é maior do que

      excede      		 \ (\ geq\)” data-valign="middle">é maior ou igual a

      é pelo menos não

      é menor que

      o mínimo      		 \ (é <\)” data-valign="middle"> menor que é

      menor do que tem

      menos do que é

      menor que      		 \ (\ leq\)” data-valign="middle">é menor ou igual a

      é no máximo não



      é mais do que o máximo