Capítulo 1 Exercícios de revisão

Exercícios de revisão de

Use a linguagem da álgebra

Identifique múltiplos e fatores

1. Use os testes de divisibilidade para determinar se 180 é divisível por 2, por 3, por 5, por 6 e por 10.

Responda

Divisível por$2,3,5,6$

2. Encontre a fatoração primária de 252.

3. Encontre o múltiplo menos comum de 24 e 40.

Responda

120

Nos exercícios a seguir, simplifique cada expressão.

4. $24÷3+4(5−2)$

5. $7+3[6−4(5−4)]−3^2$

Responda

4

Avalie uma expressão

Nos exercícios a seguir, avalie as seguintes expressões.

6. Quando$x=4$, ⓐ $x^3$ ⓑ $5x$ ⓒ $2x^2−5x+3$

7. $2x^2−4xy−3y^2$quando$x=3$ e$y=1$

Responda

3

Simplifique expressões combinando termos semelhantes

Nos exercícios a seguir, simplifique as seguintes expressões combinando termos semelhantes.

8. $12y+7+2y−5$

9. $14x^2−9x+11−8x^2+8x−6$

Responda

$6x^2−x+5$

Traduzir uma frase em inglês para uma expressão algébrica

Nos exercícios a seguir, traduza as frases em expressões algébricas.

10. ⓐ a soma de$4ab^2$ e$7a3b24ab^2$ e$7a^3b^2$

ⓑ o produto de$6y^2$ e$3y$

ⓒ doze a mais de$5x$

ⓓ$5y$ menos de$8y^2$

11. ⓐ onze vezes a diferença de$y$ e duas

ⓑ a diferença de onze vezes$y$ e duas

Responda

ⓐ$11(y−2)$
ⓑ$11y−2$

12. Dushko tem moedas e moedas de um centavo no bolso. O número de centavos é quatro, menos de cinco, o número de centavos. Deixe nn representar o número de níquel. Escreva uma expressão para o número de centavos.

Números inteiros

Simplifique expressões com valor absoluto

No exercício a seguir, preencha$<,>,$ ou$=$ para cada um dos seguintes pares de números.

13. ⓐ$−|7| \_\_\_−|−7|$

ⓑ$−8 \_\_\_−|−8|$

ⓒ$|−13| \_\_\_−13$

ⓓ$|−12| \_\_\_−(−12)$

Responda

ⓐ$=$
ⓑ$=$
ⓒ$>$
ⓓ$=$

Nos exercícios a seguir, simplifique.

14. $9−|3(4−8)|$

15. $12−3|1−4(4−2)|$

Responda

$−9$

Adicionar e subtrair números inteiros

Nos exercícios a seguir, simplifique cada expressão.

16. $−12+(−8)+7$

17. ⓐ$15−7$

ⓑ$−15−(−7)$

ⓒ$−15−7$

ⓓ$15−(−7)$

Responda

ⓐ$8$
ⓑ$−8$
ⓒ$−22$
ⓓ$22$

18. $−11−(−12)+5$

19. ⓐ$23−(−17)$ ⓑ$23+17$

Responda

ⓐ 40 ⓑ 40

20. $−(7−11)−(3−5)$

Multiplique e divida números inteiros

No exercício a seguir, multiplique ou divida.

21. ⓐ$−27÷9$ ⓑ$120÷(−8)$ ⓒ$4(−14)$ ⓓ$−1(−17)$

Responda

ⓐ$−3$ ⓑ$−15$ ⓒ$−56$ ⓓ$17$

Simplifique e avalie expressões com números inteiros

Nos exercícios a seguir, simplifique cada expressão.

22. ⓐ$(−7)^3$ ⓑ$−7^3$

23. $(7−11)(6−13)$

Responda

16

24. $63÷(−9)+(−36)÷(−4)$

25. $6−3|4(1−2)−(7−5)|$

Responda

$−12$

26. $(−2)^4−24÷(13−5)$

Para os exercícios a seguir, avalie cada expressão.

27. $(y+z)^2$quando$y=−4$ e$z=7$

Responda

9

28. $3x^2−2xy+4y^2$quando$x=−2$ e$y=−3$

Traduzir frases em inglês para expressões algébricas

Nos exercícios a seguir, traduza para uma expressão algébrica e simplifique, se possível.

29. a soma de$−4$ e$−9$, aumentada em$23$

Responda

$(−4+(−9))+23;10$

30. ⓐ a diferença de 17 e −8 ⓑ subtrai 17 de −25

Use números inteiros em aplicativos

No exercício a seguir, resolva.

31. Temperatura Em 10 de julho, a alta temperatura em Phoenix, Arizona, foi de 109°, e a alta temperatura em Juneau, Alasca, foi de 63°. Qual foi a diferença entre a temperatura em Palm Springs e a temperatura em Whitefield?

Responda

$46°$

Frações

Simplifique as frações

Nos exercícios a seguir, simplifique.

32. $\dfrac{204}{228}$

33. $−\dfrac{270x^3}{198y^2}$

Responda

$−\dfrac{15x^3}{11y^2}$

Multiplique e divida frações

Nos exercícios a seguir, execute a operação indicada.

34. $\left(−\dfrac{14}{15}\right)\left(\dfrac{10}{21}\right)$

35. $\dfrac{6x}{25}÷\dfrac{9y}{20}$

Responda

$\dfrac{8x}{15y}$

36. $\dfrac{−\frac{4}{9}}{\dfrac{8}{21}}$

Adicionar e subtrair frações

Nos exercícios a seguir, execute a operação indicada.

37. $\dfrac{5}{18}+\dfrac{7}{12}$

Responda

$\dfrac{31}{36}$

38. $\dfrac{11}{36}−\dfrac{15}{48}$

39. ⓐ$\dfrac{5}{8}+\dfrac{3}{4}$ ⓑ$\dfrac{5}{8}÷\dfrac{3}{4}$

Resposta

ⓐ$\dfrac{11}{8}$ ⓑ$\dfrac{5}{6}$

40. ⓐ$−\dfrac{3y}{10}−\dfrac{5}{6}$ ⓑ$−\dfrac{3y}{10}·\dfrac{5}{6}$

Use a ordem das operações para simplificar as frações

Nos exercícios a seguir, simplifique.

41. $\dfrac{4·3−2·5}{−6·3+2·3}$

Resposta

$−\dfrac{1}{6}$

42. $\dfrac{4(7−3)−2(4−9)}{−3(4+2)+7(3−6)}$

43. $\dfrac{4^3−4^2}{(\dfrac{4}{5})^2}$

Resposta

75

Avalie expressões variáveis com frações

Nos exercícios a seguir, avalie.

44. $4x^2y^2$quando$x=\dfrac{2}{3}$ e$y=−\dfrac{3}{4}$

45. $\dfrac{a+b}{a−b}$quando$a=−4$ e$b=6$

Resposta

$−15$

Decimais

Decimais arredondados

46. Arredonde$6.738$ para o número inteiro ⓐ centésimo ⓑ décimo ⓒ mais próximo.

Adicionar e subtrair números decimais

Nos exercícios a seguir, execute a operação indicada.

47. $−23.67+29.84$

Resposta

$6.17$

48. $54.3−100$

49. $79.38−(−17.598)$

Resposta

$96.978$

Multiplique e divida números decimais

Nos exercícios a seguir, execute a operação indicada.

50. $(−2.8)(3.97)$

51. $(−8.43)(−57.91)$

Resposta

488.1813

52. $(53.48)(10)$

53. $(0.563)(100)$

Resposta

$56.3$

54. $\$ 118.35÷2.6$

55. $1.84÷(−0.8)$

Resposta

$−23$

Converta números decimais, frações e porcentagens

Nos exercícios a seguir, escreva cada decimal como uma fração.

56. $\dfrac{13}{20}$

57. $−\dfrac{240}{25}$

Resposta

$−9.6$

Nos exercícios a seguir, converta cada fração em um decimal.

58. $−\dfrac{5}{8}$

59. $\dfrac{14}{11}$

Resposta

$1.\overline{27}$

Nos exercícios a seguir, converta cada decimal em uma porcentagem.

60. $2.43$

61. $0.0475$

Resposta

$4.75 \%$

Simplifique expressões com raízes quadradas

Nos exercícios a seguir, simplifique.

62. $\sqrt{289}$

63. $\sqrt{−121}$

Resposta

nenhum número real

Identifique números inteiros, números racionais, números irracionais e números reais

No exercício a seguir, liste os ⓐ números inteiros ⓑ inteiros ⓒ números racionais ⓓ números irracionais ⓔ números reais para cada conjunto de números

64. $−8,0,1.95286...,\dfrac{12}{5},\sqrt{36},9$

Localize frações e decimais na reta numérica

Nos exercícios a seguir, localize os números em uma reta numérica.

65. $\dfrac{3}{4},−\dfrac{3}{4},1\dfrac{1}{3},−1\dfrac{2}{3},\dfrac{7}{2},−\dfrac{5}{2}$

Resposta

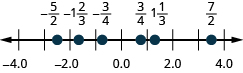
66. ⓐ$3.2$ ⓑ$−1.35$

Propriedades dos números reais

Use as propriedades comutativas e associativas

Nos exercícios a seguir, simplifique.

67. $\dfrac{5}{8}x+\dfrac{5}{12}y+\dfrac{1}{8}x+\dfrac{7}{12}y$

Resposta

$\dfrac{3}{4}x+y$

68. $−32·9·\dfrac{5}{8}$

69. $\left(\dfrac{11}{15}+\dfrac{3}{8}\right)+\dfrac{5}{8}$

Resposta

$1\dfrac{11}{15}$

Use as propriedades de identidade, inversa e zero

Nos exercícios a seguir, simplifique.

70. $\dfrac{4}{7}+\dfrac{8}{15}+\left(−\dfrac{4}{7}\right)$

71. $\dfrac{13}{15}·\dfrac{9}{17}·\dfrac{15}{13}$

Resposta

$\dfrac{9}{17}$

72. $\dfrac{0}{x−3},x\neq 3$

73. $\dfrac{5x−7}{0},5x−7\neq 0$

Resposta

indefinida

Simplifique as expressões usando a propriedade distributiva

Nos exercícios a seguir, simplifique o uso da propriedade distributiva.

74. $8(a−4)$

75. $12\left(\dfrac{2}{3}b+\dfrac{5}{6}\right)$

Resposta

$8b+10$

76. $18·\dfrac{5}{6}(2x−5)$

77. $(x−5)p$

Resposta

$xp−5p$

78. $−4(y−3)$

79. $12−6(x+3)$

Resposta

$−6x−6$

80. $6(3x−4)−(−5)$

81. $5(2y+3)−(4y−1)$

Resposta

$y+16$

Teste prático

1. Encontre a fatoração primária de$756$.

2. Combine termos semelhantes:$5n+8+2n−1$

Resposta

$7n+7$

3. Avalie quando$x=−2$ e$y=3: \dfrac{|3x−4y|}{6}$

4. Traduza para uma expressão algébrica e simplifique:

ⓐ onze a menos que menos oito

ⓑ a diferença de$−8$ e$−3$, aumentada em 5

Resposta

$−8−11 = −19$
$(−8−(−3))+5 = 0$

5. Dushko tem moedas e moedas de um centavo no bolso. O número de centavos é sete a menos de quatro vezes o número de centavos. Deixe nn representar o número de níquel. Escreva uma expressão para o número de centavos.

6. Arredonde$28.1458$ para o mais próximo

ⓐ centésimo ⓑ milésimo

Resposta

ⓐ$28.15$ ⓑ$28.146$

7. Converta

ⓐ$\dfrac{5}{11}$ com um decimal ⓑ$1.15$ em um percentual

8. Localize$\dfrac{3}{5},2.8,and−\dfrac{5}{2}$ em uma linha numérica.

Resposta

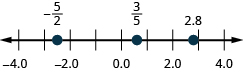
Nos exercícios a seguir, simplifique cada expressão.

9. $8+3[6−3(5−2)]−4^2$

10. $−(4−9)−(9−5)$

Resposta

1

11. $56÷(−8)+(−27)÷(−3)$

12. $16−2|3(1−4)−(8−5)|$

Resposta

$−8$

13. $−5+2(−3)^2−9$

14. $\dfrac{180}{204}$

Resposta

$\dfrac{15}{17}$

15. $−\dfrac{7}{18}+\dfrac{5}{12}$

16. $\dfrac{4}{5}÷(−\dfrac{12}{25})$

Resposta

$−\dfrac{5}{3}$

17. $\dfrac{9−3·9}{15−9}$

18. $\dfrac{4(−3+2(3−6))}{3(11−3(2+3))}$

Resposta

$3$

19. $\dfrac{5}{13}⋅\dfrac{4}{7}⋅\dfrac{13}{5}$

20. $\dfrac{−\dfrac{5}{9}}{\dfrac{10}{21}}$

Resposta

$−\dfrac{7}{6}$

21. $−4.8+(−6.7)$

22. $34.6−100$

Resposta

$−65.4$

23. $−12.04⋅(4.2)$

24. $−8÷0.05$

Resposta

160

25. $−\sqrt{121}$

26. $(\dfrac{8}{13}+\dfrac{5}{7})+\dfrac{2}{7}$

Resposta

$1\dfrac{8}{13}$

27. $5x+(−8y)−6x+3y$

28. ⓐ$\dfrac{0}{9}$ ⓑ$\dfrac{11}{0}$

Resposta

ⓐ 0 ⓑ indefinido

29. $−3(8x−5)$

30. $6(3y−1)−(5y−3)$

Resposta

$13y−3$