Skip to main content
Global

14.5 : Principe de Pascal et hydraulique

  1. Last updated
  2. Save as PDF
  • Page ID
    191732

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage
    • Principe d'État de Pascal
    • Décrire les applications du principe de Pascal
    • Déterminer les relations entre les forces dans un système hydraulique

    En 1653, le philosophe et scientifique français Blaise Pascal a publié son Traité sur l'équilibre des liquides, dans lequel il abordait les principes des fluides statiques. Un fluide statique est un fluide qui n'est pas en mouvement. Lorsqu'un fluide ne coule pas, on dit que le fluide est en équilibre statique. Si le fluide est de l'eau, on dit qu'il est en équilibre hydrostatique. Pour un fluide en équilibre statique, la force nette exercée sur n'importe quelle partie du fluide doit être nulle, sinon le fluide commencera à s'écouler.

    Les observations de Pascal, qui ont depuis été prouvées expérimentalement, constituent la base de l'hydraulique, l'un des développements les plus importants de la technologie mécanique moderne. Pascal a observé qu'un changement de pression appliqué à un fluide enfermé se transmet sans diminution à travers le fluide et aux parois de son contenant. De ce fait, nous en savons souvent plus sur la pression que sur les autres grandeurs physiques des fluides. De plus, le principe de Pascal implique que la pression totale dans un fluide est la somme des pressions provenant de différentes sources. Un bon exemple est que le fluide en profondeur dépend de la profondeur du fluide et de la pression de l'atmosphère.

    Le principe de Pascal

    Le principe de Pascal (également connu sous le nom de loi de Pascal) stipule que lorsqu'un changement de pression est appliqué à un fluide enfermé, il est transmis sans diminution à toutes les parties du fluide et aux parois de son contenant. Dans un fluide enfermé, les atomes du fluide étant libres de se déplacer, ils transmettent la pression à toutes les parties du fluide et aux parois du récipient. Tout changement de pression est transmis tel quel.

    Notez que ce principe ne signifie pas que la pression est la même en tous points d'un fluide, ce qui n'est pas vrai, puisque la pression dans un fluide proche de la Terre varie en fonction de la hauteur. Ce principe s'applique plutôt au changement de pression. Supposons que vous placiez de l'eau dans un récipient cylindrique de hauteur H et de section transversale A doté d'un piston mobile de masse m (Figure\(\PageIndex{1}\)). L'ajout de poids Mg au sommet du piston augmente la pression au sommet de\(\frac{Mg}{A}\), puisque le poids supplémentaire agit également sur la zone A du couvercle :

    \[\Delta p_{top} = \frac{Mg}{A} \ldotp\]

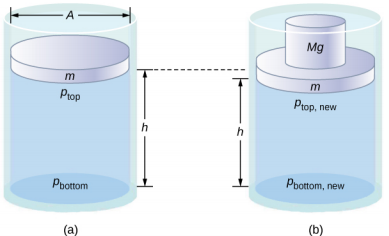
    La figure A est un dessin schématique d'un cylindre rempli de liquide et ouvert à l'atmosphère d'un côté. Un disque de masse m et de surface A identiques à la surface du cylindre est placé dans le récipient. La distance entre le disque et le fond du cylindre est h. La figure B est un schéma du cylindre avec un disque supplémentaire de masse Mg placé au sommet de la masse m provoquant le déplacement de la masse m vers le bas.
    Figure\(\PageIndex{1}\) : La pression dans un fluide change lorsque le fluide est comprimé. (a) La pression à la couche supérieure du fluide est différente de la pression à la couche inférieure. (b) L'augmentation de pression en ajoutant du poids au piston est la même partout, par exemple, p top new − p top = p bottom new − p bottom.

    Selon le principe de Pascal, la pression à tous les points de l'eau varie de la même manière\(\frac{Mg}{A}\). Ainsi, la pression au fond augmente également de\(\frac{Mg}{A}\). La pression au fond du récipient est égale à la somme de la pression atmosphérique, de la pression due au fluide et de la pression fournie par la masse. La variation de pression au fond du récipient due à la masse est

    \[\Delta p_{bottom} = \frac{Mg}{A} \ldotp\]

    Comme les variations de pression sont les mêmes partout dans le fluide, nous n'avons plus besoin d'indices pour désigner le changement de pression en haut ou en bas :

    \[\Delta p = \Delta p_{top} = \Delta p_{bottom} = \Delta p_{everywhere} \ldotp\]

    Simulation

    Pascal's Barrel est une excellente démonstration du principe de Pascal. Regardez une simulation de l'expérience de 1646 de Pascal, dans laquelle il a démontré les effets d'un changement de pression dans un fluide.

    Applications du principe de Pascal et des systèmes hydrauliques

    Les systèmes hydrauliques sont utilisés pour actionner les freins automobiles, les vérins hydrauliques et de nombreux autres systèmes mécaniques (Figure\(\PageIndex{2}\)).

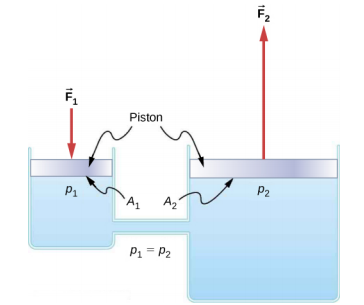
    Schéma d'un système hydraulique avec deux cylindres remplis de liquide, coiffés de pistons et reliés par un tube. Une force F1 dirigée vers le bas sur le piston gauche avec la surface A1 crée un changement de pression qui se traduit par une force ascendante F2 sur le piston droit avec la surface A2. La surface A2 est plus grande que la surface A1.
    Figure\(\PageIndex{2}\) : Un système hydraulique typique avec deux cylindres remplis de liquide, coiffés par des pistons et reliés par un tube appelé conduite hydraulique. Une force dirigée vers le bas\(\vec{F}_{1}\) sur le piston gauche crée un changement de pression qui est transmis sans diminution à toutes les parties du fluide contenu. Il en résulte une force ascendante\(\vec{F}_{2}\) sur le piston droit qui est plus importante\(\vec{F}_{1}\) que lorsque le piston droit possède une surface plus grande.

    Nous pouvons établir une relation entre les forces de ce système hydraulique simple en appliquant le principe de Pascal. Notez d'abord que les deux pistons du système sont à la même hauteur, il n'y a donc pas de différence de pression due à une différence de profondeur. La pression due à l'action de F 1 sur la zone A 1 est simplement

    \(p_{1} = \frac{F_{1}}{A_{1}}\), tel que défini par\(p = \frac{F}{A}\).

    Selon le principe de Pascal, cette pression est transmise sans diminution à travers le fluide et à toutes les parois du récipient. Ainsi, une pression p 2 est ressentie sur l'autre piston qui est égale à p 1. C'est-à-dire, p 1 = p 2. Cependant, puisque p 2 =\(\frac{F_{2}}{A_{2}}\), on voit que

    \[\frac{F_{1}}{A_{1}} = \frac{F_{2}}{A_{2}} \ldotp \label{14.12}\]

    Cette équation met en relation les rapports force/surface dans tout système hydraulique, à condition que les pistons soient à la même hauteur verticale et que le frottement dans le système soit négligeable.

    Les systèmes hydrauliques peuvent augmenter ou diminuer la force qui leur est appliquée. Pour augmenter la force, la pression est appliquée sur une plus grande surface. Par exemple, si une force de 100 N est appliquée au cylindre gauche dans la Figure 14.16 et que le cylindre droit a une surface cinq fois plus grande, la force de sortie est de 500 N. Les systèmes hydrauliques sont analogues aux simples leviers, mais ils présentent l'avantage de pouvoir envoyer la pression par des lignes courbes tortueusement à plusieurs places à la fois.

    Le vérin hydraulique est un tel système hydraulique. Un vérin hydraulique est utilisé pour soulever de lourdes charges, telles que celles utilisées par les mécaniciens automobiles pour soulever une automobile. Il s'agit d'un fluide incompressible dans un tube en U équipé d'un piston mobile de chaque côté. Un côté du tube en U est plus étroit que l'autre. Une faible force appliquée sur une petite zone peut équilibrer une force beaucoup plus importante de l'autre côté sur une plus grande surface (Figure\(\PageIndex{3}\)).

    La figure A est un schéma d'un tube en U rempli d'un fluide. Une force F1 dirigée vers le bas est appliquée sur le côté gauche avec la surface A1. Une force vers le bas F2 est appliquée sur le côté droit avec la surface A2. La surface A2 est plus grande que la surface A1. La figure B est une photo d'une voiture particulière posée sur le vérin hydraulique.
    Figure\(\PageIndex{3}\) : (a) Un vérin hydraulique fonctionne en appliquant des forces (F 1, F 2) à un fluide incompressible dans un tube en U, à l'aide d'un piston mobile (A 1, A 2) de chaque côté du tube. (b) Les vérins hydrauliques sont couramment utilisés par les mécaniciens automobiles pour soulever les véhicules afin d'effectuer les réparations et l'entretien.

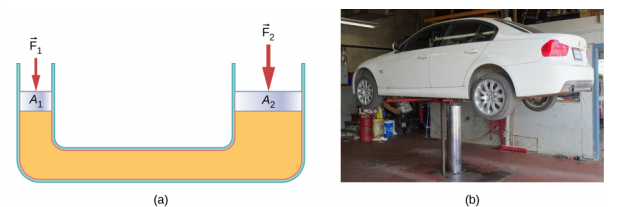
    À partir du principe de Pascal, il peut être démontré que la force nécessaire pour soulever la voiture est inférieure au poids de la voiture :

    \[F_{1} = \frac{A_{1}}{A_{2}} F_{2},\]

    où F 1 est la force appliquée pour soulever la cabine, A 1 est la section transversale du plus petit piston, A 2 est la section transversale du piston le plus gros et F 2 est le poids de la cabine.

    Exemple\(\PageIndex{1}\): Calculating Force on Wheel Cylinders: Pascal Puts on the Brakes

    Considérez le système hydraulique de l'automobile illustré à la figure\(\PageIndex{4}\). Supposons qu'une force de 100 N soit appliquée à la pédale de frein, qui agit sur le cylindre de la pédale (agissant comme un « maître-cylindre ») par l'intermédiaire d'un levier. Une force de 500 N est exercée sur le cylindre de pédale. La pression créée dans le cylindre de pédale est transmise aux quatre cylindres de roue. Le cylindre de pédale a un diamètre de 0,500 cm et chaque cylindre de roue a un diamètre de 2,50 cm. Calculez l'amplitude de la force F 2 créée au niveau de chacun des cylindres de roue.

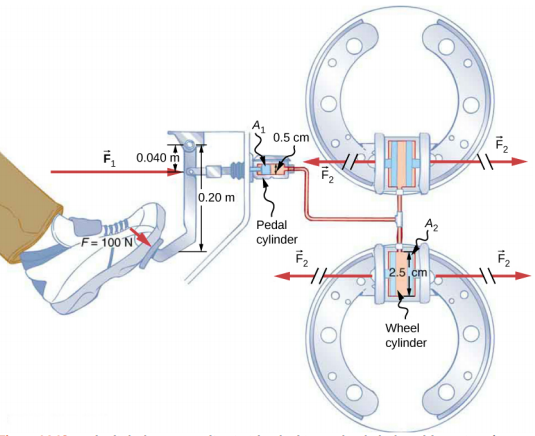
    La figure est un schéma d'un système de freinage hydraulique. Un pied est appliqué sur la pédale de frein avec la force F1. Il est transmis au cylindre de pédale avec une surface A1 de 0,5 cm. Le vérin de pédale est relié au système hydraulique par deux vérins de roue d'une surface A2 de 2,5 cm. Les cylindres de roue créent une force de sortie F2.
    Figure\(\PageIndex{4}\) : Les freins hydrauliques utilisent le principe de Pascal. Le conducteur appuie sur la pédale de frein en exerçant une force qui est augmentée par le simple levier puis par le système hydraulique. Chacun des cylindres de roue identiques reçoit la même pression et crée donc la même sortie de force F 2. Les zones de section transversale circulaire des cylindres de pédale et de roue sont représentées par A 1 et A 2, respectivement

    Stratégie

    On nous donne la force F1 appliquée au cylindre de pédale. Les surfaces transversales A 1 et A 2 peuvent être calculées à partir de leurs diamètres donnés. Ensuite, nous pouvons utiliser la relation suivante pour trouver la force F 2 :

    \[\frac{F_{1}}{A_{1}} = \frac{F_{2}}{A_{2}} \ldotp\]

    Manipulez cela de manière algébrique pour obtenir F 2 d'un côté et substituer des valeurs connues.

    Solution

    Le principe de Pascal appliqué aux systèmes hydrauliques est donné par\(\frac{F_{1}}{A_{1}} = \frac{F_{2}}{A_{2}}\) :

    \[\begin{split} F_{2} & = \frac{A_{2}}{A_{1}} F_{1} = \frac{\pi r_{2}^{2}}{\pi r_{1}^{2}} F_{1} \\ & = \frac{(1.25\; cm)^{2}}{(0.250\; cm)^{2}} \times 500\; N = 1.25 \times 10^{4}\; N \ldotp \end{split}\]

    L'importance

    Cette valeur est la force exercée par chacun des quatre cylindres de roue. Notez que nous pouvons ajouter autant de cylindres de roue que nous le souhaitons. Si chacun a un diamètre de 2,50 cm, chacun exercera 1,25 x 10 4 N. Un système hydraulique simple, par exemple d'une machine simple, peut augmenter la force mais ne peut pas effectuer plus de travail que ce qui est fait sur lui. Le travail est la force multipliée par la distance parcourue, et le cylindre de roue se déplace sur une distance plus petite que le cylindre de pédale. De plus, plus le nombre de roues ajoutées est élevé, plus la distance parcourue par chacune d'elles est petite De nombreux systèmes hydrauliques, tels que les servofreins et ceux des bulldozers, sont équipés d'une pompe motorisée qui effectue la majeure partie du travail du système.

    Exercice\(\PageIndex{1}\)

    Une presse hydraulique fonctionnerait-elle toujours correctement si un gaz est utilisé au lieu d'un liquide ?