12.4 : Contrainte, déformation et module d'élasticité (partie 1)
- Page ID
- 191477
- Expliquer les concepts de contrainte et de déformation pour décrire les déformations élastiques des matériaux
- Décrire les types de déformation élastique des objets et des matériaux
Un modèle de corps rigide est un exemple idéalisé d'objet qui ne se déforme pas sous l'action de forces extérieures. Il est très utile pour analyser des systèmes mécaniques, et de nombreux objets physiques sont en effet dans une large mesure rigides. La mesure dans laquelle un objet peut être perçu comme rigide dépend des propriétés physiques du matériau à partir duquel il est fabriqué. Par exemple, une balle de ping-pong en plastique est fragile et une balle de tennis en caoutchouc est élastique lorsqu'elle est sollicitée par des forces d'écrasement. Cependant, dans d'autres circonstances, une balle de ping-pong et une balle de tennis peuvent bien rebondir sur des corps rigides. De même, une personne qui conçoit des prothèses peut être en mesure de se rapprocher de la mécanique des membres humains en les modélisant sous forme de corps rigides ; toutefois, la véritable combinaison des os et des tissus constitue un milieu élastique.
Pour le reste de cette section, nous passons de l'examen des forces qui affectent le mouvement d'un objet à celles qui affectent la forme d'un objet. Un changement de forme dû à l'application d'une force est connu sous le nom de déformation. Même de très faibles forces sont connues pour provoquer certaines déformations. La déformation est subie par des objets ou des supports physiques sous l'action de forces extérieures, par exemple en écrasant, en pressant, en déchirant, en tordant, en cisaillant ou en séparant les objets. Dans le langage de la physique, deux termes décrivent les forces qui s'exercent sur des objets soumis à une déformation : contrainte et déformation.
La contrainte est une quantité qui décrit l'ampleur des forces à l'origine de la déformation. La contrainte est généralement définie comme la force par unité de surface. Lorsque des forces exercent une traction sur un objet et provoquent son allongement, comme l'étirement d'une bande élastique, nous appelons cette contrainte une contrainte de traction. Lorsque des forces provoquent la compression d'un objet, nous appelons cela une contrainte de compression. Lorsqu'un objet est comprimé de tous les côtés, comme un sous-marin dans les profondeurs d'un océan, nous appelons ce type de stress une contrainte globale (ou contrainte volumique). Dans d'autres situations, les forces d'action peuvent ne pas être de traction ni de compression, tout en produisant une déformation notable. Supposons, par exemple, que vous teniez un livre fermement entre les paumes de vos mains, puis que, d'une main, vous appuyez et tirez sur la couverture arrière loin de vous, tandis que de l'autre main, vous appuyez et tirez sur la couverture arrière vers vous. Dans ce cas, lorsque les forces de déformation agissent tangentiellement à la surface de l'objet, nous les appelons forces de « cisaillement » et la contrainte qu'elles provoquent est appelée contrainte de cisaillement.
L'unité de contrainte SI est le pascal (Pa). Lorsqu'un newton de force appuie sur une surface unitaire d'un mètre carré, la contrainte résultante est d'un pascal :
\[one\; pascal = 1.0\; Pa = \frac{1.0\; N}{1.0\; m^{2}} \ldotp\]
Dans le système d'unités britannique, l'unité de contrainte est « psi », qui signifie « livre par pouce carré » (lb/in 2). Une autre unité souvent utilisée pour le stress global est l'atm (atmosphère). Les facteurs de conversion sont
\[1\; psi = 6895\; Pa\; and\; 1\; Pa = 1.450 \times 10^{-4}\; psi\]
\[1\; atm = 1.013 \times 10^{5}\; Pa = 14.7\; psi \ldotp\]
Un objet ou un milieu soumis à des contraintes se déforme. La quantité qui décrit cette déformation est appelée déformation. La déformation est donnée sous la forme d'une variation fractionnelle de la longueur (sous contrainte de traction) ou du volume (sous contrainte de masse) ou de la géométrie (sous contrainte de cisaillement). Par conséquent, la déformation est un nombre sans dimension. La déformation sous contrainte de traction est appelée déformation en traction, la déformation sous contrainte apparente est appelée déformation apparente (ou déformation volumique) et celle provoquée par la contrainte de cisaillement est appelée déformation de cisaillement.
Plus la contrainte est élevée, plus la déformation est importante ; toutefois, la relation entre la déformation et la contrainte n'a pas besoin d'être linéaire. Ce n'est que lorsque la contrainte est suffisamment faible que la déformation qu'elle provoque est directement proportionnelle à la valeur de la contrainte. La constante de proportionnalité dans cette relation est appelée module d'élasticité. Dans la limite linéaire des faibles valeurs de contrainte, la relation générale entre contrainte et déformation est
\[stress = (elastic\; modulus) \times strain \ldotp \label{12.33}\]
Comme le montre l'analyse dimensionnelle de cette relation, le module d'élasticité possède la même unité physique que la contrainte, car la déformation est sans dimension.
Nous pouvons également voir dans l'équation \ ref {12.33} que lorsqu'un objet est caractérisé par une valeur élevée de module d'élasticité, l'effet de la contrainte est faible. D'autre part, un faible module d'élasticité signifie que la contrainte produit une tension importante et une déformation notable. Par exemple, une contrainte sur un élastique produit une contrainte (déformation) plus importante que la même contrainte sur un ruban en acier de mêmes dimensions, car le module d'élasticité du caoutchouc est inférieur de deux ordres de grandeur au module d'élasticité de l'acier.
Le module d'élasticité de la contrainte de traction est appelé module de Young ; celui de la contrainte d'encombrement est appelé module d'encombrement ; et celui de la contrainte de cisaillement est appelé module de cisaillement. Notez que la relation entre contrainte et déformation est une relation observée, mesurée en laboratoire. Les modules d'élasticité de divers matériaux sont mesurés dans diverses conditions physiques, telles que des températures variables, et collectés dans des tableaux de données techniques à titre de référence (tableau\(\PageIndex{1}\)). Ces tableaux sont de précieuses références pour l'industrie et pour toute personne impliquée dans l'ingénierie ou la construction. Dans la section suivante, nous discutons des relations contrainte-déformation au-delà de la limite linéaire représentée par l'équation \ ref {12.33}, dans la gamme complète de valeurs de contrainte jusqu'à un point de rupture. Dans le reste de cette section, nous étudions la limite linéaire exprimée par l'équation \ ref {12.33}.
| Matériau | Module de Young × 10 10 Pa | Module de charge × 10 10 Pa | Module de cisaillement × 10 10 Pa |
|---|---|---|---|
| Aluminium | 7,0 | 7,5 | 2,5 |
| Os (tension) | 1,6 | 0,8 | 8,0 |
| Os (compression) | 0,9 | ||
| Laiton | 9.0 | 6,0 | 3.5 |
| Brique | 1,5 | ||
| béton | 2,0 | ||
| Cuivre | 11,0 | 14,0 | 4.4 |
| Verre Crown | 6,0 | 5,0 | 2,5 |
| Granit | 4,5 | 4,5 | 2,0 |
| Cheveux (humains) | 1,0 | ||
| Bois dur | 1,5 | 1,0 | |
| Fer | 21,0 | 16,0 | 7,7 |
| Le plomb | 1,6 | 4.1 | 0,6 |
| Marbre | 6,0 | 7,0 | 2,0 |
| Nickel | 21,0 | 17,0 | 7,8 |
| Polystyrène | 3,0 | ||
| Soie | 6,0 | ||
| Fil d'araignée | 3,0 | ||
| Acier | 20,0 | 16,0 | 7,5 |
| Acétone | 0,07 | ||
| Éthanol | 0,09 | ||
| Glycérine | 0,45 | ||
| Mercure | 2,5 | ||
| Eau | 0,22 |
Contrainte de traction ou de compression, déformation et module de Young
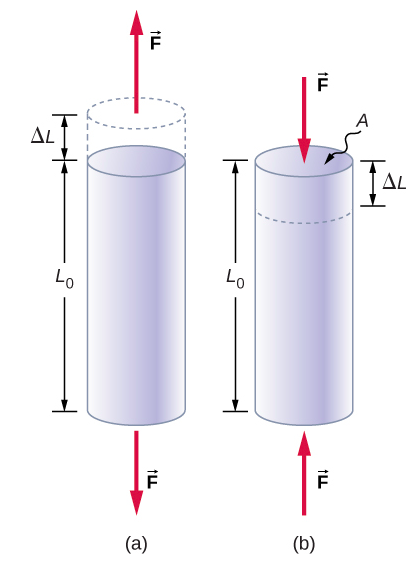
La tension ou la compression se produit lorsque deux forces antiparallèles d'égale ampleur agissent sur un objet dans une seule de ses dimensions, de telle sorte que l'objet ne bouge pas. Une façon d'envisager une telle situation est illustrée dans la Figure\(\PageIndex{1}\). Un segment de tige est étiré ou comprimé par une paire de forces agissant sur sa longueur et perpendiculairement à sa section transversale. L'effet net de ces forces est que la tige change de longueur par rapport à la longueur initiale L 0 qu'elle avait avant l'apparition des forces, à une nouvelle longueur L qu'elle possède sous l'action des forces. Ce changement de longueur\(\Delta\) L = L − L 0 peut être soit un allongement (lorsqu'il\(L\) est plus grand que la longueur initiale\(L_o\)) soit une contraction (lorsque L est inférieur à la longueur initiale L 0). Les contraintes et les déformations de traction se produisent lorsque les forces étirent un objet, provoquant son allongement, et que le changement de longueur\(\Delta L\) est positif. Les contraintes et les déformations de compression se produisent lorsque les forces contractent un objet, provoquant son raccourcissement, et que le changement de longueur\(\Delta L\) est négatif.
Dans l'une ou l'autre de ces situations, nous définissons la contrainte comme le rapport entre la force\(F_{\perp}\) de déformation et la surface transversale A de l'objet déformé. Le symbole F \(\perp\)que nous réservons à la force de déformation signifie que cette force agit perpendiculairement à la section transversale de l'objet. Les forces qui agissent parallèlement à la section transversale ne modifient pas la longueur d'un objet. La définition de la contrainte de traction est
\[tensile\; stress = \frac{F_{\perp}}{A} \ldotp \label{12.34}\]
La déformation en traction est la mesure de la déformation d'un objet soumis à une contrainte de traction et est définie comme la variation fractionnelle de la longueur de l'objet lorsque l'objet subit une contrainte de traction
\[tensile\; strain = \frac{\Delta L}{L_{0}} \ldotp \label{12.35}\]
La contrainte et la déformation en compression sont définies par les mêmes formules, les équations \ ref {12.34} et \ ref {12.35}, respectivement. La seule différence par rapport à la situation de traction est que pour les contraintes et les déformations en compression, nous prenons les valeurs absolues des côtés droits dans les équations \ ref {12.34} et \ ref {12.35}.
Le module de Young\(Y\) est le module d'élasticité lorsque la déformation est provoquée par une contrainte de traction ou de compression, et est défini par l'équation \ ref {12.33}. En divisant cette équation par la déformation en traction, nous obtenons l'expression du module de Young :
\[Y = \frac{tensile\; stress}{tensile\; strain} = \frac{\frac{F_{\perp}}{A}}{\frac{\Delta L}{L_{0}}} = \frac{F_{\perp}}{A} = \frac{L_{0}}{\Delta L} \ldotp \label{12.36}\]
Une sculpture pesant 10 000 N repose sur une surface horizontale au sommet d'un pilier vertical de 6,0 m de haut Figure\(\PageIndex{1}\). La section transversale du pilier est de 0,20 m 2 et il est fait de granit d'une densité massique de 2 700 kg/m 3. Déterminez la contrainte de compression à la section transversale située à 3,0 m en dessous du sommet du pilier et la valeur de la contrainte de compression du segment supérieur de 3,0 m du pilier.

Stratégie
Nous déterminons d'abord le poids de la partie supérieure du pilier de 3,0 m de long. La force normale qui agit sur la section transversale située à 3 m du sommet est la somme du poids du pilier et du poids de la sculpture. Une fois que nous avons obtenu la force normale, nous utilisons l'équation 12.34 pour déterminer la contrainte. Pour déterminer la déformation en compression, nous trouvons la valeur du module de Young pour le granit dans le tableau\(\PageIndex{1}\) et inversons l'équation \ ref {12.36}.
Solution
Le volume du segment de pilier avec une hauteur h = 3,0 m et une section transversale A = 0,20 m 2 est
\[V = Ah = (0.20\; m^{2})(3.0\; m) = 0.60\; m^{3} \ldotp\]
Avec une densité de granit\(\rho\) = 2,7 x 10 3 kg/m 3, la masse du segment de pilier est
\[m = \rho V = (2.7 \times 10^{3}\; kg/m^{3})(0.60\; m^{3}) = 1.60 \times 10^{3}\; kg \ldotp\]
Le poids du segment de pilier est
\[w_{p} = mg = (1.60 \times 10^{3}\; kg)(9.80\; m/s^{2}) = 1.568 \times 10^{4}\; N \ldotp\]
Le poids de la sculpture est w s = 1,0 x 10 4 N, donc la force normale sur la surface transversale située à 3,0 m sous la sculpture est
\[F_{\perp} = w_{p} + w_{s} = (1.568 + 1.0) \times 10^{4}\; N = 2.568 \times 10^{4}\; N \ldotp\]
Par conséquent, le stress est
\[stress = \frac{F_{\perp}}{A} = \frac{2.568 \times 10^{4}\; N}{0.20 m^{2}} = 1.284 \times 10^{5}\; Pa = 128.4\; kPa \ldotp\]
Le module de Young pour le granit est Y = 4,5 x 10 10 Pa = 4,5 x 10 7 kPa. Par conséquent, la contrainte de compression à cette position est
\[strain = \frac{stress}{Y} = \frac{128.4\; kPa}{4.5 \times 10^{7}\; kPa} = 2.85 \times 10^{-6} \ldotp\]
L'importance
Notez que la force normale agissant sur la section transversale du pilier n'est pas constante sur sa longueur, mais varie de sa plus petite valeur en haut à sa plus grande valeur en bas du pilier. Ainsi, si le pilier a une section transversale uniforme sur toute sa longueur, la contrainte est la plus importante à sa base.
Déterminez la contrainte de compression et la déformation à la base de la colonne de Nelson.
Une tige en acier de 2,0 m de long a une section transversale de 0,30 cm 2. La canne fait partie d'un support vertical qui soutient une lourde plate-forme de 550 kg fixée à l'extrémité inférieure de la canne. Sans tenir compte du poids de la tige, quelle est la contrainte de traction dans la tige et l'allongement de la tige sous la contrainte ?
Stratégie
Nous calculons d'abord la contrainte de traction dans la tige sous le poids de la plate-forme conformément à l'équation 12.34. Nous inversons ensuite l'équation 12.36 pour déterminer l'allongement de la tige, en utilisant L 0 = 2,0 m. À partir du tableau 12.1, le module de Young pour l'acier est Y = 2,0 x 10 11 Pa.
Solution
La substitution de valeurs numériques dans les équations nous donne
\[\begin{split} \frac{F_{\perp}}{A} & = \frac{(550\; kg)(9.8\; m/s^{2})}{3.0 \times 10^{-5}\; m^{2}} = 1.8 \times 10^{8}\; Pa \\ \Delta L & = \frac{F_{\perp}}{A} \frac{L_{0}}{Y} = (1.8 \times 10^{8}\; Pa) \left(\dfrac{2.0\; m}{2.0 \times 10^{11}\; Pa}\right) = 1.8 \times 10^{-3}\; m = 1.8\; mm \ldotp \end{split}\]
L'importance
De même que dans l'exemple avec la colonne, la contrainte de traction dans cet example n'est pas uniforme sur la longueur de la tige. Contrairement à l'exemple précédent, toutefois, si l'on prend en compte le poids de la tige, la contrainte dans la tige est la plus importante en haut et la plus faible en bas de la tige où l'équipement est fixé.
Un fil de 2,0 m de long s'étire de 1,0 mm lorsqu'il est soumis à une charge. Quelle est la contrainte de traction du fil ?
Les objets peuvent souvent subir à la fois des contraintes de compression et des contraintes de traction simultanément Figure\(\PageIndex{3}\). Un exemple est une longue étagère chargée de livres lourds qui s'affaisse entre les supports d'extrémité sous le poids des livres. La surface supérieure de l'étagère est soumise à une contrainte de compression et la surface inférieure de l'étagère est soumise à une contrainte de traction. De même, les poutres longues et lourdes s'affaissent sous leur propre poids. Dans la construction de bâtiments modernes, ces contraintes de flexion peuvent être presque éliminées grâce à l'utilisation de poutres en I Figure\(\PageIndex{4}\).


Un coffre lourd repose sur une table soutenue par trois colonnes. Regardez cette démonstration pour déplacer la boîte et voir comment la compression (ou tension) des colonnes est affectée lorsque la boîte change de position.


