Skip to main content
Global

12.3 : Exemples d'équilibre statique

  1. Last updated
  2. Save as PDF
  • Page ID
    191495

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage
    • Identifier et analyser les situations d'équilibre statique
    • Établissez un diagramme du corps libre pour un objet étendu en équilibre statique
    • Définir et résoudre des conditions d'équilibre statique pour des objets en équilibre dans diverses situations physiques

    Tous les exemples de ce chapitre sont des problèmes planaires. Par conséquent, nous utilisons les conditions d'équilibre sous la forme des composantes des équations 12.2.9 à 12.2.11. Nous avons introduit une stratégie de résolution de problèmes dans l'exemple 12.1 pour illustrer la signification physique des conditions d'équilibre. Nous généralisons maintenant cette stratégie dans une liste d'étapes à suivre pour résoudre les problèmes d'équilibre statique des corps rigides étendus. Nous procédons en cinq étapes pratiques.

    Stratégie de résolution de problèmes : équilibre statique
    1. Identifiez l'objet à analyser. Pour certains systèmes en équilibre, il peut être nécessaire de prendre en compte plus d'un objet. Identifiez toutes les forces agissant sur l'objet. Identifiez les questions auxquelles vous devez répondre. Identifiez les informations fournies dans le problème. Dans le cas de problèmes réalistes, certaines informations clés peuvent être implicites dans la situation plutôt que fournies explicitement.
    2. Établissez un diagramme du corps libre pour l'objet. (a) Choisissez le référentiel xy pour le problème. Dessinez un diagramme du corps libre de l'objet, en incluant uniquement les forces qui agissent sur celui-ci. Le cas échéant, représentez les forces en termes de leurs composantes dans le référentiel choisi. Lorsque vous effectuez cette opération pour chaque force, barrez la force d'origine afin de ne pas inclure deux fois par erreur la même force dans les équations. Étiquetez toutes les forces ; vous en aurez besoin pour calculer correctement les forces nettes dans les directions x et y. Pour une force inconnue, la direction doit être attribuée de manière arbitraire ; considérez cela comme une « direction de travail » ou une « direction soupçonnée ». La direction correcte est déterminée par le signe que vous obtenez dans la solution finale. Un signe plus (+) signifie que la direction de travail est la direction réelle. Un signe moins (−) signifie que la direction réelle est opposée à la direction de travail supposée. (b) Choisissez l'emplacement de l'axe de rotation ; en d'autres termes, choisissez le point de pivot par rapport auquel vous allez calculer les couples des forces d'action. Sur le schéma du corps libre, indiquez l'emplacement du pivot et des bras de levier des forces d'action ; vous en aurez besoin pour calculer correctement les couples. Lors de la sélection du pivot, gardez à l'esprit que le pivot peut être placé où vous le souhaitez, mais le principe directeur est que le meilleur choix simplifiera autant que possible le calcul du couple net le long de l'axe de rotation.
    3. Définissez les équations d'équilibre de l'objet. (a) Utilisez le diagramme du corps libre pour écrire une condition d'équilibre correcte (équation 12.2.9) pour les composantes de force dans la direction x. (b) Utilisez le diagramme du corps libre pour écrire une condition d'équilibre correcte (équation 12.2.13) pour les composantes de force dans la direction y. (c) Utiliser le diagramme du corps libre pour écrire une condition d'équilibre correcte (équation 12.2.11) pour les couples le long de l'axe de rotation. Utilisez l'équation 12.2.12 pour évaluer les magnitudes et les sens du couple.
    4. Simplifiez et résolvez le système d'équations pour l'équilibre afin d'obtenir des quantités inconnues. À ce stade, votre travail ne porte que sur l'algèbre. N'oubliez pas que le nombre d'équations doit être identique au nombre d'inconnues. Si le nombre d'inconnues est supérieur au nombre d'équations, le problème ne peut pas être résolu.
    5. Évaluez les expressions pour les quantités inconnues que vous avez obtenues dans votre solution. Vos réponses finales doivent avoir des valeurs numériques et des unités physiques correctes. Si ce n'est pas le cas, suivez les étapes précédentes pour retrouver l'origine de l'erreur et la corriger. Vous pouvez également vérifier indépendamment vos réponses numériques en déplaçant le pivot vers un autre emplacement et en résolvant à nouveau le problème, comme nous l'avons fait dans l'exemple 12.1.

    Notez que la mise en place d'un diagramme du corps libre pour un problème d'équilibre du corps rigide est l'élément le plus important du processus de solution. Sans une configuration correcte et un schéma correct, vous ne serez pas en mesure de noter les conditions d'équilibre correctes. Notez également qu'un diagramme de corps libre pour un corps rigide étendu susceptible de subir un mouvement de rotation est différent d'un diagramme de corps libre pour un corps qui ne subit que des mouvements de translation (comme vous l'avez vu dans les chapitres sur les lois du mouvement de Newton). En dynamique translationnelle, un corps est représenté par son CM, où toutes les forces exercées sur le corps sont liées et aucun couple n'apparaît. Cela n'est pas vrai en dynamique de rotation, où un corps rigide étendu ne peut pas être représenté par un seul point. En effet, lors de l'analyse de la rotation, nous devons identifier les couples agissant sur le corps, et le couple dépend à la fois de la force d'action et de son bras de levier. Ici, le schéma du corps libre d'un corps rigide allongé nous aide à identifier les couples externes.

    Exemple 12.3 : L'équilibre du couple

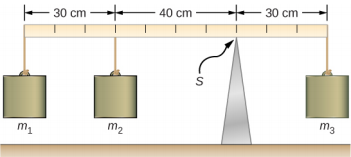
    Trois masses sont fixées à un manomètre uniforme, comme le montre la figure\(\PageIndex{1}\). La masse du capteur est de 150,0 g et les masses situées à gauche du pivot sont m 1 = 50,0 g et m 2 = 75,0 g. Déterminez la masse m3 qui équilibre le système lorsqu'il est fixé à l'extrémité droite de la manette, et la force de réaction normale au point d'appui lorsque le système est équilibré.

    La figure est un dessin schématique d'un balancier de couple, d'une poutre horizontale supportée par un point d'appui (indiqué par S) et de trois masses fixées des deux côtés du point d'appui. La masse 3 se trouve à 30 cm à droite de S. La masse 2 est à 40 cm à gauche de S. La masse 1 se trouve à 30 cm à gauche de la masse 2.
    Figure\(\PageIndex{1}\) : Dans une balance de couple, une poutre horizontale est supportée par un point d'appui (indiqué par S) et des masses sont fixées des deux côtés du point d'appui. Le système est en équilibre statique lorsque le faisceau ne tourne pas. Il est équilibré lorsque le faisceau reste plat.

    Stratégie

    Pour la disposition illustrée sur la figure, nous identifions les cinq forces suivantes agissant sur le manomètre :

    1. w 1 = m 1 g est le poids de la masse m 1 ;
    2. w 2 = m 2 g est le poids de la masse m 2 ;
    3. w = mg est le poids de l'ensemble du compteur ;
    4. w 3 = m 3 g est le poids de la masse inconnue m 3 ;
    5. F S est la force de réaction normale au point d'appui S.

    Nous choisissons un cadre de référence dans lequel la direction de l'axe y est la direction de la gravité, la direction de l'axe x se trouve le long du manche du mètre et l'axe de rotation (l'axe z) est perpendiculaire à l'axe x et passe par le point d'appui S. En d'autres termes, nous choisissons le pivot au point où le manomètre touche le support. Il s'agit d'un choix naturel pour le pivot, car ce point ne bouge pas lorsque le bâton tourne. Nous sommes maintenant prêts à configurer le diagramme du corps libre pour le manomètre. Nous indiquons le pivot et attachons cinq vecteurs représentant les cinq forces le long de la ligne représentant le manomètre, en localisant les forces par rapport à la figure pivot\(\PageIndex{2}\). À ce stade, nous pouvons identifier les bras de levier des cinq forces sur la base des informations fournies dans le problème. Pour les trois masses suspendues, le problème est explicite quant à leur emplacement le long du bâton, mais l'information concernant l'emplacement du poids w est donnée implicitement. Le mot clé ici est « uniforme ». Nos études précédentes nous ont appris que le CM d'un bâton uniforme est situé à son point médian, c'est donc là que nous attachons le poids w, à la marque des 50 cm.

    La figure est un dessin schématique de la répartition des forces pour un balancier de couple, une poutre horizontale supportée par un point d'appui (indiqué par S) et trois masses fixées des deux côtés du point d'appui. La force Fs au point S pointe vers le haut. La force w3, à droite du point S et séparée par la distance r3, pointe vers le bas. Les forces w, w2 et w1 se trouvent à gauche du point S et pointent vers le bas. Ils sont séparés par les distances r, r2 et r1, respectivement.
    Figure\(\PageIndex{2}\) : Schéma du corps libre du manomètre. Le pivot est choisi au point d'appui S.
    Solution

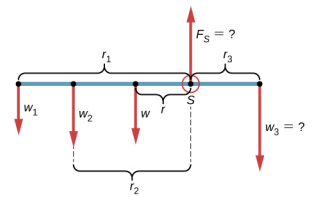
    Avec Figure\(\PageIndex{1}\) et Figure\(\PageIndex{2}\) pour référence, nous commençons par trouver les bras de levier des cinq forces agissant sur le manche :

    \[\begin{split} r_{1} & = 30.0\; cm + 40.0\; cm = 70.0\; cm \\ r_{2} & = 40.0\; cm \\ r & = 50.0\; cm - 30.0\; cm = 20.0\; cm \\ r_{S} & = 0.0\; cm\; (because\; F_{S}\; is\; attached\; at\; the\; pivot) \\ r_{3} & = 30.0\; cm \ldotp \end{split}\]

    Nous pouvons maintenant trouver les cinq couples par rapport au pivot choisi :

    \[\begin{split} \tau_{1} & = +r_{1} w_{1} \sin 90^{o} = +r_{1} m_{1} g \quad (counterclockwise\; rotation,\; positive\; sense) \\ \tau_{2} & = +r_{2} w_{2} \sin 90^{o} = +r_{2} m_{2} g \quad (counterclockwise\; rotation,\; positive\; sense) \\ \tau & = +rw \sin 90^{o} = +rmg \quad \quad \quad (gravitational\; torque) \\ \tau_{S} & = r_{S} F_{S} \sin \theta_{S} = 0 \quad \quad \quad \quad \quad (because\; r_{S} = 0\; cm) \\ \tau_{3} & = -r_{3} w_{3} \sin 90^{o} = -r_{3} m_{3} g \quad (counterclockwise\; rotation,\; negative\; sense) \end{split}\]

    La deuxième condition d'équilibre (équation pour les couples) pour le manomètre est

    \[\tau_{1} + \tau_{2} + \tau + \tau_{S} + \tau_{3} = 0 \ldotp\]

    En substituant des valeurs de couple dans cette équation, nous pouvons omettre les couples donnant une contribution nulle. De cette façon, la deuxième condition d'équilibre est

    \[+r_{1} m_{1} g + r_{2} m_{2} g + rmg - r_{3} m_{3} g = 0 \ldotp \label{12.17}\]

    En sélectionnant la direction +y à laquelle elle doit être parallèle\(\vec{F}_{S}\), la première condition d'équilibre du stick est

    \[-w_{1} - w_{2} - w + F_{S} - w_{3} = 0 \ldotp\]

    En substituant les forces, la première condition d'équilibre devient

    \[-m_{1} g - m_{2} g - mg + F_{S} - m_{3} g = 0 \ldotp \label{12.18}\]

    Nous résolvons ces équations simultanément pour les valeurs inconnues m 3 et F S. Dans l'équation \ ref {12.17}, nous annulons le facteur g et réorganisons les termes pour obtenir

    \[r_{3} m_{3} = r_{1} m_{1} + r_{2} m_{2} + rm \ldotp\]

    Pour obtenir m 3, on divise les deux côtés par r 3, donc on a

    \[\begin{split} m_{3} & = \frac{r_{1}}{r_{3}} m_{1} + \frac{r_{2}}{r_{3}} m_{2} + \frac{r}{r_{3}} m \\ & = \frac{70}{30} (50.0\; g) + \frac{40}{30} (75.0\; g) + \frac{20}{30} (150.0\; g) = 315.0 \left(\dfrac{2}{3}\right)\; g \simeq 317\; g \ldotp \end{split} \label{12.19}\]

    Pour déterminer la force de réaction normale, nous réorganisons les termes de l'équation \ ref {12.18}, en convertissant les grammes en kilogrammes :

    \[\begin{split} F_{S} & = (m_{1} + m_{2} + m + m_{3}) g \\ & = (50.0 + 75.0 + 150.0 + 316.7) \times (10^{-3}\; kg) \times (9.8\; m/s^{2}) = 5.8\; N \ldotp \end{split} \label{12.20}\]

    L'importance

    Notez que l'équation \ ref {12.17} est indépendante de la valeur de g. La balance de couple peut donc être utilisée pour mesurer la masse, car les variations des valeurs g à la surface de la Terre n'affectent pas ces mesures. Ce n'est pas le cas pour une balance à ressort car elle mesure la force.

    Exercice 12.3

    Répétez l'exemple 12.3 en utilisant l'extrémité gauche du manomètre pour calculer les couples, c'est-à-dire en plaçant le pivot à l'extrémité gauche du manomètre.

    Dans l'exemple suivant, nous montrons comment utiliser la première condition d'équilibre (équation des forces) sous la forme vectorielle donnée par l'équation 12.2.9 et l'équation 12.2.10. Nous présentons cette solution pour illustrer l'importance d'un choix approprié de référentiel. Bien que tous les repères inertiels soient équivalents et que les solutions numériques obtenues dans un cadre soient les mêmes que dans n'importe quel autre, un choix inapproprié de référentiel peut rendre la solution assez longue et complexe, alors qu'un choix judicieux de référentiel rend la solution simple. Nous le montrons dans la solution équivalente au même problème. Cet exemple particulier illustre une application de l'équilibre statique à la biomécanique.

    Exemple 12.4 : Forces exercées sur l'avant-bras

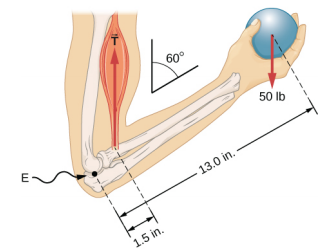
    Un haltérophile tient un poids de 50,0 livres (équivalent à 222,4 N) avec son avant-bras, comme le montre la figure\(\PageIndex{3}\). Son avant-bras est positionné à\(\beta\) = 60° par rapport au haut de son bras. L'avant-bras est soutenu par une contraction du muscle biceps, qui provoque un couple autour du coude. En supposant que la tension du biceps agit dans la direction verticale donnée par la gravité, quelle tension le muscle doit-il exercer pour maintenir l'avant-bras dans la position indiquée ? Quelle est la force exercée sur l'articulation du coude ? Supposons que le poids de l'avant-bras soit négligeable. Donnez vos réponses finales en unités SI.

    La figure est un dessin schématique d'un avant-bras pivoté autour du coude. Une balle de 50 livres est tenue dans la paume. La distance entre le coude et le ballon est de 13 pouces. La distance entre le coude et le muscle biceps, qui provoque un couple autour du coude, est de 1,5 pouce. L'avant-bras forme un angle de 60 degrés avec le haut du bras.
    Figure\(\PageIndex{3}\) : L'avant-bras est entraîné en rotation autour du coude (E) par une contraction du muscle biceps, ce qui provoque une tension\(\vec{T}_{M}\).

    Stratégie

    Nous identifions trois forces agissant sur l'avant-bras : la force inconnue\(\vec{F}\) au niveau du coude, la tension inconnue\(\vec{T}_{M}\) dans le muscle et le poids d'\(\vec{w}\)une magnitude w = 50 livres. Nous adoptons le cadre de référence avec l'axe X le long de l'avant-bras et le pivot au niveau du coude. La direction verticale est la direction du poids, qui est la même que la direction du haut du bras. L'axe X forme un angle\(\beta\) = 60° avec la verticale. L'axe Y est perpendiculaire à l'axe X. Nous établissons maintenant le diagramme du corps libre pour l'avant-bras. Nous dessinons d'abord les axes, le pivot et les trois vecteurs représentant les trois forces identifiées. Ensuite, nous localisons l'angle\(\beta\) et représentons chaque force par ses composantes x et y, en n'oubliant pas de barrer le vecteur de force d'origine pour éviter un double comptage. Enfin, nous étiquetons les forces et leurs bras de levier. Le schéma du corps libre de l'avant-bras est illustré sur la figure\(\PageIndex{4}\). À ce stade, nous sommes prêts à établir des conditions d'équilibre pour l'avant-bras. Chaque force possède des composantes x et y ; par conséquent, nous avons deux équations pour la première condition d'équilibre, une équation pour chaque composante de la force nette agissant sur l'avant-bras.

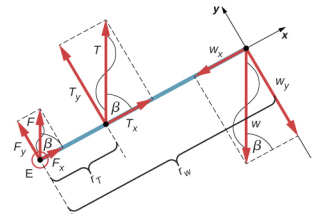
    La figure est un schéma du corps libre pour l'avant-bras. La force F est appliquée au point E. La force T est appliquée à la distance r tau du point E. La force W est appliquée du côté opposé séparé par r w du point E. Les projections des forces sur les axes x et y sont présentées. Les forces F et T forment un angle bêta avec l'axe x. La force W forme un angle bêta avec une ligne la reliant à sa projection sur l'axe y.
    Figure\(\PageIndex{4}\) : Schéma du corps libre pour l'avant-bras : le pivot est situé au point E (coude).

    Notez que dans notre cadre de référence, les contributions à la deuxième condition d'équilibre (pour les couples) proviennent uniquement des composantes y des forces, car les composantes x des forces sont toutes parallèles à leurs bras de levier, de sorte que pour chacune d'entre elles, nous avons sin\(\theta\) = 0 dans l'équation 12.2.12. Pour les composantes y, nous avons\(\theta\) = ± 90° dans l'équation 12.2.12. Notez également que le couple de la force au niveau du coude est nul car cette force est attachée au pivot. La contribution au couple net provient donc uniquement des couples de T y et de w y.

    Solution

    Nous voyons sur le diagramme du corps libre que la composante x de la force nette satisfait l'équation

    \[+F_{x} + T_{x} - w_{x} = 0 \label{12.21}\]

    et la composante y de la force nette satisfait

    \[+F_{y} + T_{y} - w_{y} = 0 \ldotp \label{12.22}\]

    L'équation \ ref {12.21} et l'équation \ ref {12.22} sont deux équations de la première condition d'équilibre (pour les forces). Ensuite, nous lisons sur le diagramme du corps libre que le couple net le long de l'axe de rotation est

    \[+r_{T} T_{y} - r_{w} w_{y} = 0 \ldotp \label{12.23}\]

    L'équation \ ref {12.23} est la deuxième condition d'équilibre (pour les couples) pour l'avant-bras. Le diagramme du corps libre montre que les bras de levier mesurent r T = 1,5 pouce et r w = 13,0 pouces. À ce stade, nous n'avons pas besoin de convertir les pouces en unités SI, car tant que ces unités sont cohérentes dans l'équation 12.23, elles s'annulent. En utilisant à nouveau le diagramme du corps libre, nous trouvons les amplitudes des forces qui les composent :

    \[\begin{split} F_{x} & = F \cos \beta = F \cos 60^{o} = \frac{F}{2} \\ T_{x} & = T \cos \beta = T \cos 60^{o} = \frac{T}{2} \\ w_{x} & = w \cos \beta = w \cos 60^{o} = \frac{w}{2} \\ F_{y} & = F \sin \beta = F \sin 60^{o} = \frac{F \sqrt{3}}{2} \\ T_{y} & = T \sin \beta = T \sin 60^{o} = \frac{T \sqrt{3}}{2} \\ w_{y} & = w \sin \beta = w \sin 60^{o} = \frac{w \sqrt{3}}{2} \ldotp \end{split}\]

    Nous substituons ces magnitudes dans l'équation \ ref {12.21}, l'équation \ ref {12.22} et l'équation \ ref {12.23} pour obtenir, respectivement,

    \[\begin{split} \frac{F}{2} + \frac{T}{2} - \frac{w}{2} & = 0 \\ \frac{F \sqrt{3}}{2} + \frac{T \sqrt{3}}{2} - \frac{w \sqrt{3}}{2} & = 0 \\ \frac{r_{T} T \sqrt{3}}{2} - \frac{r_{w} w \sqrt{3}}{2} & = 0 \ldotp \end{split}\]

    Lorsque nous simplifions ces équations, nous constatons qu'il ne nous reste que deux équations indépendantes pour les deux magnitudes de force inconnues, F et T, car l'équation \ ref {12.21} pour la composante x est équivalente à l'équation \ ref {12.22} pour la composante y. De cette façon, nous obtenons la première condition d'équilibre pour les forces

    \[F + T - w = 0 \label{12.24}\]

    et la deuxième condition d'équilibre pour les couples

    \[r_{T} T - r_{w} w = 0 \ldotp \label{12.25}\]

    L'amplitude de la tension dans le muscle est obtenue en résolvant l'équation \ ref {12.25} :

    \[T = \frac{r_{w}}{r_{T}} w =frac{13.0}{1.5} (50\; lb) = 433 \frac{1}{3}\; lb \simeq 433.3\; lb \ldotp\]

    La force au niveau du coude est obtenue en résolvant l'équation \ ref {12.24} :

    \[F = w - T = 50.0\; lb - 433.3\; lb = -383.3\; lb \ldotp\]

    Le signe négatif de l'équation indique que la force réelle exercée sur le coude est antiparallèle à la direction de travail adoptée pour dessiner le diagramme du corps libre. Dans la réponse finale, nous convertissons les forces en unités de force SI. La réponse est

    \[F = 383.3\; lb = 383.3(4.448\; N) = 1705\; N\; downward\]

    \[T = 433.3\; lb = 433.3(4.448\; N) = 1927\; N\; upward \ldotp\]

    L'importance

    Deux points importants méritent d'être soulignés à cet égard. La première concerne la conversion en unités SI, qui peut être effectuée à la toute fin de la solution tant que nous maintenons la cohérence des unités. Le deuxième problème important concerne les articulations telles que le coude. Lors de l'analyse initiale d'un problème, les articulations doivent toujours être supposées exercer une force dans une direction arbitraire, puis vous devez résoudre toutes les composantes d'une force de charnière de manière indépendante. Dans cet exemple, la force du coude se trouve être verticale car le problème suppose que la tension exercée par les biceps est également verticale. Une telle simplification n'est toutefois pas une règle générale.

    Solution 2

    Supposons que nous adoptions un cadre de référence avec la direction de l'axe Y le long du poids de 50 livres et que le pivot soit placé au niveau du coude. Dans ce cadre, les trois forces n'ont que des composantes y, donc nous n'avons qu'une seule équation pour la première condition d'équilibre (pour les forces). Nous dessinons le diagramme du corps libre de l'avant-bras, comme indiqué sur la figure\(\PageIndex{5}\), en indiquant le pivot, les forces d'action et leurs bras de levier par rapport au pivot, ainsi que les angles\(\theta_{T}\) et les angles\(\theta_{w}\) que les forces\(\vec{T}_{M}\) et\(\vec{w}\) (respectivement) font avec leurs bras de levier. Dans la définition du couple donnée par l'équation 12.2.12, l'angle\(\theta_{T}\) est l'angle de direction du vecteur\(\vec{T}_{M}\), compté dans le sens antihoraire à partir de la direction radiale du bras de levier qui pointe toujours à l'opposé du pivot. Selon la même convention, l'angle\(\theta_{w}\) est mesuré dans le sens antihoraire à partir de la direction radiale du bras de levier par rapport au vecteur\(\vec{w}\). Ainsi, les couples non nuls sont plus facilement calculés en les substituant directement dans l'équation 12.2.12 comme suit :

    \[\tau_{T} = r_{T} T \sin \theta_{T} = r_{T} T \sin \beta = r_{T} T \sin 60^{o} = + \frac{r_{T} T \sqrt{3}}{2}\]

    \[\tau_{w} = r_{w} w \sin \theta_{w} = r_{w} w \sin (\beta + 180^{o}) = -r_{w} w \sin \beta = - \frac{r_{w} w \sqrt{3}}{2} \ldotp\]

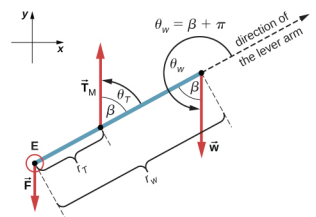
    La figure est un schéma du corps libre pour l'avant-bras. La force F est appliquée au point E. La force Tm est appliquée à la distance r tau du point E. La force W est appliquée du côté opposé séparé par r w du point E. Les projections des forces sur les axes x et y sont présentées. La force Tm forme un angle thêta tau égal à bêta avec la direction du bras de levier. La force W forme un angle thêta w égal à la somme de beta et de Pi avec la direction du bras de levier.
    Figure\(\PageIndex{5}\) : Schéma du corps libre de l'avant-bras pour la solution équivalente. Le pivot est situé au point E (coude).

    La deuxième condition d'équilibre,\(\tau_{T}\) +\(\tau_{w}\) = 0, peut maintenant être écrite sous la forme

    \[\frac{r_{T} T \sqrt{3}}{2} - \frac{r_{w} w \sqrt{3}}{2} = 0 \ldotp \label{12.26}\]

    À partir du diagramme du corps libre, la première condition d'équilibre (pour les forces) est

    \[-F + T - w = 0 \ldotp \label{12.27}\]

    L'équation \ ref {12.26} est identique à l'équation \ ref {12.25} et donne le résultat T = 433,3 livres. L'équation \ ref {12.27} donne

    \[F = T - w = 433.3\; lb - 50.0\; lb = 383.3\; lb\]

    Nous voyons que ces réponses sont identiques à nos réponses précédentes, mais le second choix pour le référentiel conduit à une solution équivalente plus simple et plus rapide car elle ne nécessite pas de résoudre les forces dans leurs composantes rectangulaires.

    Exercice 12.4

    Répétez l'exemple 12.4 en supposant que l'avant-bras est un objet de densité uniforme qui pèse 8,896 N.

    Exemple 12.5 : Une échelle adossée à un mur

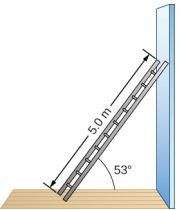
    Une échelle uniforme mesure L = 5,0 m de long et pèse 400,0 N. L'échelle repose contre un mur vertical glissant, comme le montre la figure\(\PageIndex{6}\). L'angle d'inclinaison entre l'échelle et le sol rugueux est\(\beta\) de 53°. Déterminez les forces de réaction du sol et du mur de l'échelle et le coefficient de frottement statique\(\mu_{s}\) à l'interface de l'échelle avec le plancher qui empêche l'échelle de glisser.

    La figure est un dessin schématique d'une échelle de 5,0 m de long reposant contre un mur. L'échelle forme un angle de 53 degrés avec le sol.
    Figure\(\PageIndex{6}\) A Une échelle de 5,0 m de long repose contre un mur résistant au frottement.

    Stratégie

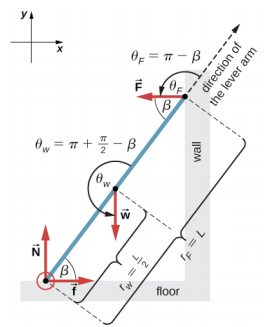
    Nous pouvons identifier quatre forces agissant sur l'échelle. La première force est la force de réaction normale N provenant du sol dans la direction verticale vers le haut. La deuxième force est la force de friction statique f =\(\mu_{s}\) N dirigée horizontalement le long du sol vers le mur. Cette force empêche l'échelle de glisser. Ces deux forces agissent sur l'échelle à son point de contact avec le sol. La troisième force est le poids w de l'échelle, fixé à son CM situé à mi-chemin entre ses extrémités. La quatrième force est la force de réaction normale F de la paroi dans la direction horizontale opposée à la paroi, fixée au point de contact avec la paroi. Il n'y a aucune autre force car le mur est glissant, ce qui signifie qu'il n'y a pas de friction entre le mur et l'échelle. Sur la base de cette analyse, nous adoptons le cadre de référence avec l'axe y dans la direction verticale (parallèle au mur) et l'axe x dans la direction horizontale (parallèle au sol). Dans ce cadre, chaque force possède soit une composante horizontale, soit une composante verticale, mais pas les deux, ce qui simplifie la solution. Nous sélectionnons le pivot au point de contact avec le sol. Dans le diagramme du corps libre de l'échelle, nous indiquons le pivot, les quatre forces et leurs bras de levier, ainsi que les angles entre les bras de levier et les forces, comme indiqué sur la figure\(\PageIndex{7}\). Avec notre choix de l'emplacement du pivot, aucun couple ne provient de la force de réaction normale N ou du frottement statique f, car ils agissent tous deux au niveau du pivot.

    La figure est un schéma à corps libre représentant une échelle qui forme un angle bêta avec le sol et repose contre un mur. La force N est appliquée au point du sol et est perpendiculaire au sol. La force W est appliquée au milieu de l'échelle. La force F est appliquée au point qui repose sur le mur et est perpendiculaire au mur. La force W forme un angle theta w avec la direction du bras de levier. Thêta w est égal à la somme de Pi et de la moitié de Pi avec le bêta soustrait. La force F forme un angle thêta F avec la direction du bras de levier. Thêta F est égal au Pi moins bêta.
    Figure\(\PageIndex{7}\) : Schéma du corps libre d'une échelle reposant contre un mur sans friction.
    Solution

    D'après le diagramme du corps libre, la force nette dans la direction x est

    \[+f - F = 0 \label{12.28}\]

    la force nette dans la direction y est

    \[+ N - w = 0 \label{12.29}\]

    et le couple net le long de l'axe de rotation au point de pivot est

    \[\tau_{w} + \tau_{F} = 0 \ldotp \label{12.30}\]

    où\(\tau_{w}\) est le couple du poids w et\(\tau_{F}\) le couple de la réaction F. À partir du diagramme du corps libre, nous avons identifié que le bras de levier de la réaction au niveau de la paroi est r F = L = 5,0 m et que le bras de levier du poids est r w\(\frac{L}{2}\) = = 2,5 m. À l'aide du diagramme à corps libre, nous déterminons les angles à utiliser dans l'équation 12.2.12 pour les couples :\(\theta_{F}\) = 180° −\(\beta\) pour le couple résultant de la force de réaction avec la paroi, et\(\theta_{w}\) = 180° + (90° −\(\beta\)) pour le couple dû au poids. Nous sommes maintenant prêts à utiliser l'équation 12.2.12 pour calculer les couples :

    \[\tau_{w} = r_{w} w \sin \theta_{w} = r_{w} w \sin (180^{o} + 90^{o} - \beta) = - \frac{L}{2} w \sin (90^{o} - \beta) = - \frac{L}{2} w \cos \beta\]

    \[tau_{F} = r_{F} F \sin \theta_{F} = r_{F} F \sin (180^{o} - \beta) = LF \sin \beta \ldotp\]

    Nous remplaçons les couples dans l'équation \ ref {12.30} et résolvons pour F :

    \[- \frac{L}{2} w \cos \beta + LF \sin \beta = 0 \label{12.31}\]

    \[F = \frac{w}{2} \cot \beta = \frac{400.0\; N}{2} \cot 53^{o} = 150.7\; N\]

    Nous obtenons la force de réaction normale avec le sol en résolvant l'équation \ ref {12.29} : N = w = 400,0 N. L'amplitude du frottement est obtenue en résolvant l'équation \ ref {12.28} : f = F = 150,7 N. Le coefficient de frottement statique est\(\mu_{s}\) =\(\frac{f}{N}\) =\(\frac{150.7}{400.0}\) = 0,377.

    La force nette exercée sur l'échelle au point de contact avec le sol est la somme vectorielle de la réaction normale du sol et des forces de friction statiques :

    \[\vec{F}_{floor} = \vec{f} + \vec{N} = (150.7\; N)(- \hat{i}) + (400.0\; N)(+ \hat{j}) = (-150.7\; \hat{i} + 400.0\; \hat{j}) N \ldotp\]

    Son ampleur est

    \[F_{floor} = \sqrt{f^{2} + N^{2}} = \sqrt{150.7^{2} + 400.0^{2}}\; N = 427.4\; N\]

    et sa direction est

    \[\varphi = \tan^{-1} \left(\dfrac{N}{f}\right) = \tan^{-1} \left(\dfrac{400.0}{150.7}\right) = 69.3^{o}\; above\; the\; floor \ldotp\]

    Il convient de souligner ici deux observations générales d'application pratique. Tout d'abord, notez que lorsque nous choisissons un point pivot, il n'est pas prévu que le système pivote réellement autour du point choisi. Dans cet exemple, l'échelle ne tourne pas du tout mais repose fermement sur le sol ; néanmoins, son point de contact avec le sol constitue un bon choix pour le pivot. Ensuite, remarquez que lorsque nous utilisons l'équation 12.2.12 pour calculer les couples individuels, nous n'avons pas besoin de résoudre les forces en leurs composantes normales et parallèles par rapport à la direction du bras de levier, et nous n'avons pas besoin de prendre en compte la sensation du couple. Tant que l'angle de l'équation 12.2.12 est correctement identifié, à l'aide d'un diagramme à corps libre, comme étant l'angle mesuré dans le sens antihoraire entre la direction du bras de levier et la direction du vecteur de force, l'équation 12.2.12 donne à la fois l'amplitude et la signification du couple. En effet, le couple est le produit vectoriel du vecteur levier bras croisé avec le vecteur force, et l'équation 12.2.12 exprime la composante rectangulaire de ce produit vectoriel le long de l'axe de rotation.

    L'importance

    Ce résultat est indépendant de la longueur de l'échelle car L est annulé dans la deuxième condition d'équilibre, Équation \ ref {12.31}. Quelle que soit la longueur ou la longueur de l'échelle, tant que son poids est de 400 N et que son angle avec le sol est de 53°, nos résultats sont valables. Mais l'échelle glissera si le couple net devient négatif dans l'équation \ ref {12.31}. Cela se produit pour certains angles lorsque le coefficient de frottement statique n'est pas suffisamment élevé pour empêcher l'échelle de glisser.

    Exercice 12.5

    Pour la situation décrite dans l'exemple 12.5, déterminez les valeurs du coefficient\(\mu_{s}\) de frottement statique pour lequel l'échelle commence à glisser, étant donné que β est l'angle que fait l'échelle avec le sol.

    Exemple 12.6 : Forces exercées sur les charnières de porte

    Une porte battante qui pèse w = 400,0 N est soutenue par des charnières A et B de sorte que la porte puisse pivoter autour d'un axe vertical passant par les charnières Figure\(\PageIndex{8}\). La porte a une largeur de b = 1,00 m et la dalle de porte a une densité de masse uniforme. Les charnières sont placées symétriquement sur le bord de la porte de manière à ce que le poids de la porte soit réparti uniformément entre elles. Les charnières sont séparées par une distance a = 2,00 m. Déterminez les forces qui s'exercent sur les charnières lorsque la porte est à moitié ouverte.

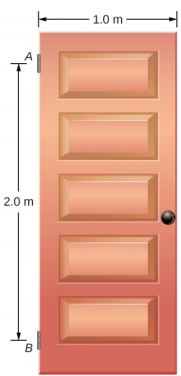
    La figure est un dessin schématique d'une porte verticale pivotante soutenue par deux charnières fixées aux points A et B. La distance entre les points A et B est de 2 mètres. La porte mesure un mètre de large.
    Figure\(\PageIndex{8}\) : Une porte verticale pivotante 400-N est soutenue par deux charnières fixées aux points A et B.

    Stratégie

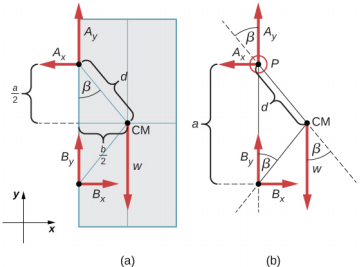
    Les forces que la porte exerce sur ses charnières peuvent être déterminées en inversant simplement le sens des forces que les charnières exercent sur la porte. Notre tâche consiste donc à trouver les forces exercées par les charnières de la porte. Trois forces agissent sur la dalle de la porte : une force inconnue\(\vec{A}\) provenant de la charnière A, une force inconnue\(\vec{B}\) provenant de la charnière B et le poids connu\(\vec{w}\) fixé au centre de masse de la dalle de porte. Le CM est situé au centre géométrique de la porte car la dalle a une densité de masse uniforme. Nous adoptons un cadre de référence rectangulaire avec l'axe y le long de la direction de la gravité et l'axe x dans le plan de la dalle, comme indiqué dans le panneau (a) de la figure\(\PageIndex{9}\), et résolvons toutes les forces dans leurs composantes rectangulaires. De cette façon, nous avons quatre composantes de forces inconnues : deux composantes de force\(\vec{A}\) (A x et A y) et deux composantes de force\(\vec{B}\) (B x et B y). Dans le diagramme du corps libre, nous représentons les deux forces au niveau des charnières par leurs composantes vectorielles, dont les orientations supposées sont arbitraires. Comme il existe quatre inconnues (A x, B x, A y et B y), nous devons établir quatre équations indépendantes. L'une des équations est la condition d'équilibre des forces dans la direction X. La deuxième équation est la condition d'équilibre des forces dans la direction y. La troisième équation est la condition d'équilibre des couples en rotation autour d'une charnière. Comme le poids est réparti uniformément entre les charnières, nous avons la quatrième équation, A y = B y. Pour définir les conditions d'équilibre, nous dessinons un diagramme à corps libre et choisissons le point de pivot sur la charnière supérieure, comme indiqué dans le panneau (b) de la figure\(\PageIndex{9}\). Enfin, nous résolvons les équations pour les composantes de force inconnues et trouvons les forces.

    La figure A est une représentation géométrique d'une porte verticale pivotante soutenue par deux charnières fixées aux points A et B. Les forces A et B sont appliquées aux points A et B. Des projections de ces forces sur les axes x et y sont présentées. La force w est appliquée au point CM. Le point CM est plus bas que le point A d'un demi-a et se trouve à droite du point A d'un demi-b. La ligne allant du point A au point CM forme un angle bêta avec le bord du mur. La figure B est un schéma à corps libre d'une porte verticale pivotante soutenue par deux charnières fixées aux points A et B. La force Ay forme un angle bêta avec la ligne reliant les points P et CM. Force By forme un angle bêta avec la ligne reliant les points B et CM. La force W forme un angle bêta avec la droite qui est le prolongement de la ligne reliant les points P et CM. La distance entre les points P et CM est d.
    Figure\(\PageIndex{9}\) : (a) Géométrie et (b) schéma de la carrosserie libre de la porte.
    Solution

    À partir du diagramme du corps libre de la porte, nous avons la première condition d'équilibre des forces :

    dans la direction x, $$-A_ {x} + B_ {x} = 0 \ Flèche droite A_ {x} + B_ {x} $ dans la direction y, $/7 A_ {y} + B_ {y} - w = 0 \ Flèche droite A_ {y} = B_ {y} = \ frac {w} {2} = \ frac {400,0 \ N ;} {2} = 200,0 \ ; N \ ldotp \]

    Nous sélectionnons le pivot au point P (charnière supérieure, selon le diagramme du corps libre) et écrivons la deuxième condition d'équilibre pour les couples de rotation autour du point P :

    pivot à P : $$ \ tau_ {w} + \ tau_ {Bx} + \ tau_ {Par} = 0 \ ldotp \ label {12,32} \]

    Nous utilisons le diagramme du corps libre pour trouver tous les termes de cette équation :

    \[\begin{split} \tau_{w} & = dw \sin (- \beta) = -dw \sin \beta = -dw \frac{\frac{b}{2}}{d} = -w \frac{b}{2} \\ \tau_{Bx} & = a B_{x} \sin 90^{o} = + a B_{x} \\ \tau_{By} & = a B_{y} \sin 180^{o} = 0 \ldotp \end{split}\]

    Pour évaluer le péché\(\beta\), nous utilisons la géométrie du triangle représenté dans la partie (a) de la figure. Maintenant, nous substituons ces couples dans l'équation \ ref {12.32} et calculons B x :

    pivot en P : $$-w \ frac {b} {2} + a B_ {x} = 0 \ Flèche droite B_ {x} = w \ frac {b} {2a} = (400,0 \ ; N) \ frac {1} {2 \ ; \ cdotp 2} = 100,0 \ ; N \ ldotp \]

    Par conséquent, les amplitudes des forces des composantes horizontales sont A x = B x = 100,0 N. Les forces exercées sur la porte sont

    à la charnière supérieure : $$ \ vec {F} _ {A \ ; sur \ ; porte} = -100,0 \ ; N \ ; \ hat {i} + 200,0 \ ; N \ ; \ hat {j} $à la charnière inférieure : $$ \ vec {F} _ {B \ ; sur \ ; porte} = +100,0 \ ; N \ ; \ hat {i} + 200,0 \ ; N \ ; \ hat {j} \ ldotp \]

    Les forces qui s'exercent sur les charnières proviennent de la troisième loi de Newton, comme

    sur la charnière supérieure : $$ \ vec {F} _ {porte \ ; on \ ; A} = 100,0 \ ; N \ ; \ hat {i} - 200,0 \ ; N \ ; \ hat {j} $sur la charnière inférieure : $$ \ vec {F} _ {porte \ ; on \ ; B} = - 100,0 \ ; N \ ; N \ ; \ hat {i} - 200,0 \ ; N \ ; \ hat {j} \ ldotp \]

    L'importance

    Notez que si le problème était formulé sans supposer que le poids soit réparti de manière égale entre les deux charnières, nous ne serions pas en mesure de le résoudre car le nombre d'inconnues serait supérieur au nombre d'équations exprimant des conditions d'équilibre.

    Exercice 12.6

    Résolvez le problème de l'exemple 12.6 en prenant la position de pivot au centre de gravité.

    Exercice 12.7

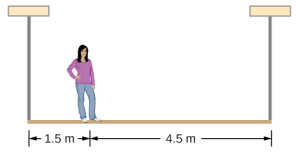
    Une personne de 50 kg se tient à 1,5 m d'une extrémité d'un échafaudage uniforme de 6,0 m de long et pesant 70,0 kg. Déterminez les tensions dans les deux cordes verticales qui soutiennent l'échafaudage.

    La figure est un dessin schématique d'une femme debout à 1,5 m d'une extrémité et à 4,5 m de l'autre extrémité d'un échafaudage.

    Exercice 12.8

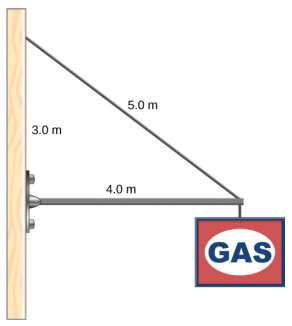
    Un panneau 400,0-N est suspendu à l'extrémité d'une entretoise uniforme. L'entretoise mesure 4,0 m de long et pèse 600,0 N. Elle est soutenue par une charnière fixée au mur et par un câble dont l'autre extrémité est attachée au mur à 3,0 m au-dessus de l'extrémité gauche de l'entretoise. Déterminez la tension du câble de support et la force de la charnière sur l'entretoise.

    La figure est un dessin schématique d'un panneau suspendu à l'extrémité d'une entretoise uniforme. L'entretoise mesure 4,0 m de long et est soutenue par un câble de 5,0 m de long attaché au mur à un point situé à 3,0 m au-dessus de l'extrémité gauche de l'entretoise.