12.2 : Conditions d'équilibre statique
- Page ID
- 191487
- Identifier les conditions physiques de l'équilibre statique.
- Dessinez un diagramme de corps libre pour un corps rigide soumis à l'action de forces.
- Expliquez comment les conditions d'équilibre nous permettent de résoudre les problèmes de statique.
Nous disons qu'un corps rigide est en équilibre lorsque ses accélérations linéaire et angulaire sont nulles par rapport à un référentiel inertiel. Cela signifie qu'un corps en équilibre peut se déplacer, mais si c'est le cas, ses vitesses linéaires et angulaires doivent être constantes. Nous disons qu'un corps rigide est en équilibre statique lorsqu'il est au repos dans le cadre de référence que nous avons sélectionné. Notez que la distinction entre l'état de repos et un état de mouvement uniforme est artificielle, c'est-à-dire qu'un objet peut être au repos dans notre cadre de référence sélectionné, alors que pour un observateur se déplaçant à une vitesse constante par rapport à notre cadre, le même objet semble être en mouvement uniforme à vitesse constante. Comme le mouvement est relatif, ce qui est en équilibre statique pour nous est en équilibre dynamique pour l'observateur en mouvement, et vice versa. Les lois de la physique étant identiques pour tous les repères inertiels, dans un référentiel inertiel, il n'y a aucune distinction entre l'équilibre statique et l'équilibre.
Selon la deuxième loi du mouvement de Newton, l'accélération linéaire d'un corps rigide est provoquée par une force nette agissant sur celui-ci, ou
\[\sum_{k} \vec{F}_{k} = m \vec{a}_{CM} \ldotp \label{12.1}\]
Ici, la somme est de toutes les forces externes agissant sur le corps, où m est sa masse et\(\vec{a}_{CM}\) est l'accélération linéaire de son centre de masse (un concept que nous avons discuté dans Momentum linéaire et collisions sur le moment linéaire et les collisions). À l'équilibre, l'accélération linéaire est nulle. Si nous mettons l'accélération à zéro dans l'équation \ ref {12.1}, nous obtenons l'équation suivante :
La première condition d'équilibre pour l'équilibre statique d'un corps rigide exprime l'équilibre translationnel :
\[\sum_{k} \vec{F}_{k} = \vec{0} \ldotp \label{12.2}\]
La première condition d'équilibre, l'équation \ ref {12.2}, est la condition d'équilibre des forces, que nous avons rencontrée lors de l'étude des applications des lois de Newton.
Cette équation vectorielle est équivalente aux trois équations scalaires suivantes pour les composantes de la force nette :
\[\sum_{k} F_{kx} = 0,\; \sum_{k} F_{ky} = 0,\; \sum_{k} F_{kz} = 0 \ldotp \label{12.3}\]
De manière analogue à l'équation \ ref {12.1}, nous pouvons affirmer que l'accélération\(\vec{\alpha}\) de rotation d'un corps rigide autour d'un axe de rotation fixe est provoquée par le couple net agissant sur le corps, ou
\[\sum_{k} \vec{\tau}_{k} = I \vec{\alpha} \ldotp \label{12.4}\]
Ici, I est l'inertie rotationnelle du corps en rotation autour de cet axe et la somme est globale à tous les couples\(\vec{\tau}_{k}\) des forces externes dans l'équation \ ref {12.2}. À l'équilibre, l'accélération de rotation est nulle. En mettant à zéro le côté droit de l'équation \ ref {12.4}, nous obtenons la deuxième condition d'équilibre :
La deuxième condition d'équilibre pour l'équilibre statique d'un corps rigide exprime l'équilibre rotationnel :
\[\sum_{k} \vec{\tau}_{k} = \vec{0} \ldotp \label{12.5}\]
La deuxième condition d'équilibre, Équation \ ref {12.5}, est la condition d'équilibre des couples que nous avons rencontrée lors de l'étude de la dynamique de rotation. Il convient de noter que cette équation d'équilibre est généralement valable pour l'équilibre rotationnel autour de n'importe quel axe de rotation (fixe ou non). Encore une fois, cette équation vectorielle équivaut à trois équations scalaires pour les composantes vectorielles du couple net :
\[\sum_{k} \tau_{kx} = 0,\; \sum_{k} \tau_{ky} = 0,\; \sum_{k} \tau_{kz} = 0 \ldotp \label{12.6}\]
La deuxième condition d'équilibre signifie qu'à l'équilibre, il n'y a aucun couple externe net susceptible de provoquer une rotation autour d'un axe. Les première et deuxième conditions d'équilibre sont énoncées dans un référentiel particulier. La première condition ne fait intervenir que des forces et est donc indépendante de l'origine du référentiel. Cependant, la deuxième condition implique le couple, qui est défini comme un produit croisé\(\vec{\tau}_{k} = \vec{r}_{k} \times \vec{F}_{k}\), où le vecteur de position\(\vec{r}_{k}\) par rapport à l'axe de rotation du point où la force est appliquée entre dans l'équation. Le couple dépend donc de l'emplacement de l'axe dans le référentiel. Cependant, lorsque les conditions d'équilibre de rotation et de translation sont maintenues simultanément dans un cadre de référence, elles le sont également dans tout autre référentiel inertiel, de sorte que le couple net autour de n'importe quel axe de rotation est toujours nul. L'explication de cette situation est assez simple.
Supposons que le vecteur\(\vec{R}\) est la position de l'origine d'un nouveau référentiel inertiel S'dans l'ancien référentiel inertiel S. De notre étude du mouvement relatif, nous savons que dans le nouveau référentiel S', le vecteur\(\vec{r}′_{k}\) de position du point où la force\(\vec{F}_{k}\) est appliquée est lié à l'\(\vec{r}_{k}\)aide de l'équation
\[\vec{r}'_{k} = \vec{r}_{k} - \vec{R} \ldotp\]
Nous pouvons maintenant additionner tous les couples\(\vec{\tau}'_{k} = \vec{r}'_{k} \times \vec{F}_{k}\) de toutes les forces externes dans un nouveau référentiel, S' :
\[\sum_{k} \vec{\tau}'_{k} = \sum_{k} \vec{r}'_{k} \times \vec{F}_{k} = \sum_{k} (\vec{r}_{k} - \vec{R}) \times \vec{F}_{k} = \sum_{k} \vec{r}_{k} \times \vec{F}_{k} - \sum_{k} \vec{R} \times \vec{F}_{k} = \sum \vec{\tau}_{k} - \vec{R} \times \sum_{k} \vec{F}_{k} = \vec{0} \ldotp\]
Dans la dernière étape de cette chaîne de raisonnement, nous avons utilisé le fait qu'en équilibre dans l'ancien cadre de référence, S, le premier terme disparaît à cause de l'équation \ ref {12.5} et le second terme disparaît à cause de l'équation \ ref {12.2}. Nous voyons donc que le couple net dans tout référentiel inertiel S'est nul, à condition que les deux conditions d'équilibre se maintiennent dans un référentiel inertiel \ ref {S}.
Cela implique en pratique que lorsque nous appliquons des conditions d'équilibre à un corps rigide, nous sommes libres de choisir n'importe quel point comme origine du référentiel. Notre choix du référentiel est dicté par les spécificités physiques du problème que nous sommes en train de résoudre. Dans un cadre de référence, la forme mathématique des conditions d'équilibre peut être assez compliquée, alors que dans un autre cadre, les mêmes conditions peuvent avoir une forme mathématique plus simple et facile à résoudre. L'origine d'un cadre de référence sélectionné est appelée point pivot.
Dans le cas le plus général, les conditions d'équilibre sont exprimées par les six équations scalaires (équations \ ref {12.3} et \ ref {12.6}). Pour les problèmes d'équilibre planaire avec rotation autour d'un axe fixe, que nous examinerons dans ce chapitre, nous pouvons réduire le nombre d'équations à trois. La procédure standard consiste à adopter un cadre de référence où l'axe z est l'axe de rotation. Avec ce choix d'axe, le couple net n'a qu'une composante z, toutes les forces qui ont des couples non nuls se situent dans le plan xy, et donc les contributions au couple net proviennent uniquement des composantes x et y des forces externes. Ainsi, pour les problèmes planaires avec l'axe de rotation perpendiculaire au plan xy, nous avons les trois conditions d'équilibre suivantes pour les forces et les couples :
\[F_{1x} + F_{2x} + \cdots + F_{Nx} = 0 \label{12.7}\]
\[F_{1y} + F_{2y} + \cdots + F_{Ny} = 0 \label{12.8}\]
\[\tau_{1} + \tau_{2} + \cdots + \tau_{N} = 0 \label{12.9}\]
où la somme est calculée sur l'ensemble des N forces extérieures agissant sur le corps et sur leurs couples. Dans l'équation \ ref {12.9}, nous avons simplifié la notation en supprimant l'indice z, mais nous comprenons ici que la somme est globale de toutes les contributions le long de l'axe z, qui est l'axe de rotation. Dans l'équation \ ref {12.9}, la composante z \(\vec{\tau}_{k}\)du couple produit par la force\(\vec{F}_{k}\) est
\[\tau_{k} = r_{k} F_{k} \sin \theta \label{12.10}\]
où r k est la longueur du bras de levier de la force et F k est l'amplitude de la force (comme vous l'avez vu dans Rotation à axe fixe). L'angle\(\theta\) est l'angle entre les vecteurs\(\vec{r}_{k}\) et\(\vec{F}_{k}\), mesuré d'un vecteur\(\vec{r}_{k}\) à l'autre\(\vec{F}_{k}\) dans le sens antihoraire (Figure\(\PageIndex{1}\)). Lorsque vous utilisez l'équation \ ref {12.10}, nous calculons souvent l'amplitude du couple et lui attribuons un sens positif (+) ou négatif (−), en fonction du sens de rotation provoqué par ce seul couple. Dans l'équation \ ref {12.9}, le couple net est la somme des termes, chaque terme étant calculé à partir de l'équation \ ref {12.10}, et chaque terme doit avoir le bon sens. De même, dans l'équation \ ref {12.7}, nous attribuons le signe + aux composantes de force dans la direction x + et le signe − aux composantes dans la direction − x. La même règle doit être systématiquement suivie dans l'équation \ ref {12.8}, lors du calcul des composantes de force le long de l'axe y.
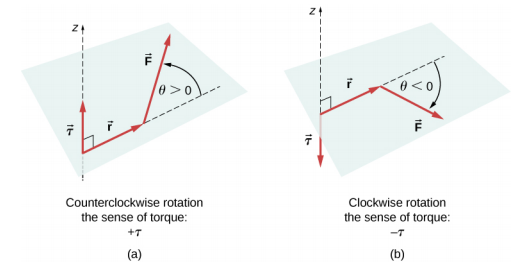
Regardez cette démonstration pour voir deux forces agir sur un carré rigide en deux dimensions. À tout moment, les conditions d'équilibre statique données par l'équation \ ref {12.7} à l'équation \ ref {12.9} sont satisfaites. Vous pouvez faire varier l'ampleur des forces et de leurs bras de levier et observer l'effet de ces changements sur le carré.
Dans de nombreuses situations d'équilibre, l'une des forces qui agissent sur le corps est son poids. Dans les diagrammes de corps libres, le vecteur de poids est attaché au centre de gravité du corps. À toutes fins pratiques, le centre de gravité est identique au centre de masse, comme vous l'avez appris dans Momentum linéaire et collisions sur le moment linéaire et les collisions. Ce n'est que dans les situations où un corps a une grande extension spatiale, de sorte que le champ gravitationnel n'est pas uniforme dans tout son volume, que le centre de gravité et le centre de masse sont situés à des points différents. Dans la pratique, cependant, même des objets aussi grands que des bâtiments ou des navires de croisière sont situés dans un champ gravitationnel uniforme à la surface de la Terre, où l'accélération due à la gravité a une magnitude constante de g = 9,8 m/s 2. Dans ces situations, le centre de gravité est identique au centre de gravité. Par conséquent, tout au long de ce chapitre, nous utilisons le centre de gravité (CM) comme point auquel le vecteur de poids est attaché. Rappelons que le CM a une signification physique particulière : lorsqu'une force externe est appliquée à un corps exactement à son CM, le corps dans son ensemble subit un mouvement de translation et une telle force ne provoque pas de rotation.
Lorsque le CM est situé hors de l'axe de rotation, un couple gravitationnel net se produit sur un objet. Le couple gravitationnel est le couple causé par le poids. Ce couple gravitationnel peut faire tourner l'objet si aucun support n'est présent pour l'équilibrer. L'amplitude du couple gravitationnel dépend de la distance à laquelle se trouve le CM par rapport au pivot. Par exemple, dans le cas d'un camion à benne basculante (Figure\(\PageIndex{2}\)), le pivot est situé sur la ligne où les pneus entrent en contact avec la surface de la route. Si le CM est situé au-dessus de la surface de la route, le couple gravitationnel peut être suffisamment important pour faire basculer le camion. Les voitures particulières équipées d'un CM bas, situées à proximité de la chaussée, résistent mieux au renversement que les camions.
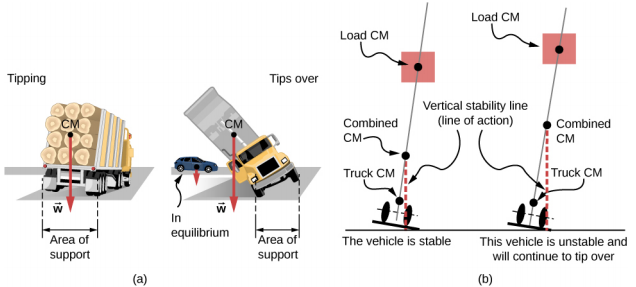
Si vous inclinez un boîtier de telle sorte qu'un bord reste en contact avec la table située en dessous, un bord de la base du support devient un pivot. Tant que le centre de gravité du boîtier reste au-dessus de la base du support, le couple gravitationnel fait pivoter le boîtier vers sa position initiale d'équilibre stable. Lorsque le centre de gravité se déplace à l'extérieur de la base du support, le couple gravitationnel fait tourner le boîtier dans la direction opposée et le boîtier se retourne. Regardez cette démonstration pour tester les positions stables et instables d'une boîte.
Une voiture particulière avec un empattement de 2,5 m pèse 52 % de son poids sur les roues avant sur un sol plat, comme l'illustre la Figure 12.4. Où se trouve le CM de cette voiture par rapport à l'essieu arrière ?
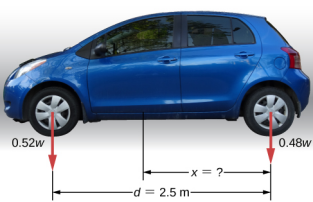
Stratégie
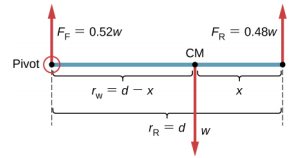
Nous ne connaissons pas le poids w de la voiture. Tout ce que nous savons, c'est que lorsque la voiture repose sur une surface plane, 0,52 W appuie sur la surface aux points de contact des roues avant et 0,48 W sur la surface aux points de contact des roues arrière. De plus, les points de contact sont séparés les uns des autres par la distance d = 2,5 m. À ces points de contact, la voiture subit des forces de réaction normales de magnitudes F F = 0,52 w et F R = 0,48 w sur les essieux avant et arrière, respectivement. Nous savons également que la voiture est un exemple de carrosserie rigide en équilibre dont le poids total w agit au niveau de son CM. Le CM est situé quelque part entre les points où agissent les forces de réaction normales, quelque part à une distance x du point où F R agit. Notre tâche consiste à trouver x. Ainsi, nous identifions trois forces agissant sur la carrosserie (la voiture), et nous pouvons dessiner un diagramme de corps libre pour la carrosserie rigide étendue, comme le montre la figure\(\PageIndex{4}\).
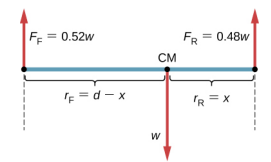
Nous sommes presque prêts à écrire les conditions d'équilibre de l'équation \ ref {12.7} à l'équation \ ref {12.9} pour la voiture, mais nous devons d'abord choisir le référentiel. Supposons que nous choisissions l'axe X sur la longueur de la voiture, l'axe Y vertical et l'axe z perpendiculaire à ce plan xy. Avec ce choix, il suffit d'écrire l'équation \ ref {12.7} et l'équation \ ref {12.9} car toutes les composantes y sont identiques à zéro. Nous devons maintenant décider de l'emplacement du point pivot. Nous pouvons choisir n'importe quel point comme emplacement de l'axe de rotation (axe z). Supposons que nous placions l'axe de rotation en CM, comme indiqué sur le schéma de carrosserie libre de la voiture. À ce stade, nous sommes prêts à écrire les conditions d'équilibre de la voiture.
Solution
Chaque condition d'équilibre ne contient que trois termes, car N = 3 forces agissent sur la voiture. La première condition d'équilibre, Équation \ ref {12.7}, se lit comme suit
\[+F_{F} - w + F_{R} = 0 \ldotp \label{12.11}\]
Cette condition est satisfaite de manière triviale, car lorsque nous substituons les données, l'équation \ ref {12.11} devient +0,52 w − w + 0,48 w = 0. La deuxième condition d'équilibre, Équation \ ref {12.9}, se lit comme suit
\[\tau_{F} + \tau_{w} + \tau_{R} = 0 \label{12.12}\]
où\(\tau_{F}\) est le couple de la force F F,\(\tau_{w}\) est le couple gravitationnel de la force w et\(\tau_{R}\) est le couple de la force F R. Lorsque le pivot est situé à CM, le couple gravitationnel est identique à zéro car le bras de levier du poids par rapport à un axe passant par CM est nul. Les lignes d'action des deux forces de réaction normales sont perpendiculaires à leurs bras de levier, donc dans l'équation \ ref {12.10}, nous avons |sin\(\theta\) | = 1 pour les deux forces. À partir du diagramme du corps libre, nous lisons que le couple\(\tau_{F}\) provoque une rotation dans le sens des aiguilles d'une montre autour du pivot en CM, donc son sens est négatif ; et le couple\(\tau_{R}\) provoque une rotation dans le sens antihoraire autour du pivot en CM, de sorte que son sens est positif. Avec ces informations, nous écrivons la deuxième condition d'équilibre comme
\[-r_{F} F_{F} + r_{R} F_{R} = 0 \ldotp \label{12.13}\]
À l'aide du diagramme du corps libre, nous identifions les amplitudes de force F R = 0,48 w et F F = 0,52 w, ainsi que leurs bras de levier correspondants r R = x et r F = d − x. Nous pouvons maintenant écrire la deuxième condition d'équilibre, Équation \ ref {12.13}, explicitement en termes de distance inconnue x :
\[-0.52(d - x)w + 0.48xw = 0 \ldotp \label{12.14}\]
Ici, le poids w s'annule et nous pouvons résoudre l'équation pour la position inconnue x du CM. La réponse est x = 0,52d = 0,52 (2,5 m) = 1,3 m. Solution Le choix du pivot à la position de l'essieu avant ne modifie pas le résultat. Le diagramme du corps libre correspondant à cet emplacement de pivot est présenté à la Figure 12.6. Pour ce choix de point pivot, la deuxième condition d'équilibre est
\[-r_{w} w + r_{R} F_{R} = 0 \ldotp \label{12.15}\]
Lorsque nous remplaçons les quantités indiquées sur le schéma, nous obtenons
\[-(d - x)w + 0.48dw = 0 \ldotp \label{12.16}\]
La réponse obtenue en résolvant l'équation \ ref {12.13} est, encore une fois, x = 0,52d = 1,3 m.
L'importance
Cet exemple montre que lors de la résolution de problèmes d'équilibre statique, nous sommes libres de choisir l'emplacement du pivot. Pour différents choix du point pivot, nous avons différents ensembles de conditions d'équilibre à résoudre. Cependant, tous les choix mènent à la même solution au problème.
Résolvez l'exemple 12.1 en choisissant le pivot à l'emplacement de l'essieu arrière.
Expliquez laquelle des situations suivantes satisfait aux deux conditions d'équilibre : (a) une balle de tennis qui ne tourne pas lorsqu'elle se déplace dans les airs ; (b) un pélican qui plane dans les airs à une vitesse constante à une altitude donnée ; ou (c) un vilebrequin dans le moteur d'une voiture garée.
Un cas particulier d'équilibre statique se produit lorsque toutes les forces externes sur un objet agissent au niveau ou le long de l'axe de rotation ou lorsque l'extension spatiale de l'objet peut être ignorée. Dans ce cas, l'objet peut être traité efficacement comme une masse ponctuelle. Dans ce cas particulier, nous n'avons pas à nous soucier de la deuxième condition d'équilibre, Equation \ ref {12.9}, car tous les couples sont identiques à zéro et la première condition d'équilibre (pour les forces) est la seule condition à être satisfaite. Le diagramme du corps libre et la stratégie de résolution de problèmes pour ce cas particulier ont été décrits dans Newton's Laws of Motion and Applications of Newton's Laws. Dans l'exemple suivant, vous verrez une situation d'équilibre typique impliquant uniquement la première condition d'équilibre.
Regardez cette démonstration pour voir trois poids reliés par des cordes sur des poulies et attachés ensemble en un nœud. Vous pouvez expérimenter les poids pour voir comment ils affectent la position d'équilibre du nœud et, en même temps, voir la représentation sous forme de diagramme vectoriel de la première condition d'équilibre à l'œuvre.
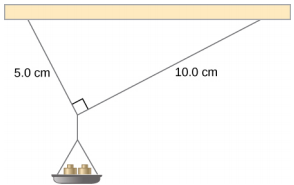
Un petit plateau d'une masse de 42,0 g est soutenu par deux cordes, comme le montre la Figure 12.7. La tension maximale que la ficelle peut supporter est de 2,80 N. La masse est ajoutée progressivement à la poêle jusqu'à ce que l'une des cordes se brise. De quelle corde s'agit-il ? Quelle quantité de masse faut-il ajouter pour que cela se produise ?
Stratégie
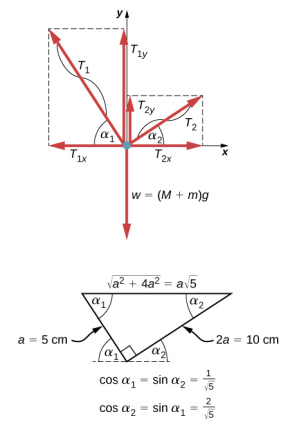
Ce système mécanique composé de cordes, de masses et de plateau est en équilibre statique. Plus précisément, le nœud qui lie les cordes au plateau est en équilibre statique. Le nœud peut être traité comme un point ; par conséquent, nous n'avons besoin que de la première condition d'équilibre. Les trois forces qui s'exercent sur le nœud sont la tension\(\vec{T}_{1}\) de la corde de 5,0 cm, la tension\(\vec{T}_{2}\) de la corde de 10,0 cm et le poids\(\vec{w}\) du plateau qui contient les masses. Nous adoptons un système de coordonnées rectangulaires avec l'axe y pointant à l'opposé de la direction de la gravité et dessinons le diagramme du corps libre pour le nœud (voir Figure 12.8). Pour trouver les composantes de tension, nous devons identifier les angles de direction\(\alpha_{1}\) et\(\alpha_{2}\) que les cordes forment avec la direction horizontale qui est l'axe X. Comme vous pouvez le voir sur la Figure 12.7, les chaînes forment les deux côtés d'un triangle droit. Nous pouvons utiliser le théorème de Pythagore pour résoudre ce triangle, illustré à la Figure 12.8, et trouver le sinus et le cosinus des angles\(\alpha_{1}\) et\(\alpha_{2}\). Ensuite, nous pouvons résoudre les tensions dans leurs composantes rectangulaires, remplacer l'équilibre dans la première condition (Équation \ ref {12.7} et Équation \ ref {12.8}) et résoudre les tensions dans les cordes. La corde la plus tendue se cassera en premier.
Solution
Le poids w qui tire sur le nœud est dû à la masse M du pan et à la masse m ajoutée au plateau, ou w = (M + m) g. À l'aide du diagramme du corps libre de la Figure 12.8, nous pouvons définir les conditions d'équilibre pour le nœud :
dans la direction x,\[-T_{1x} + T_{2x} = 0\] dans la direction y,\[+T_{1y} + T_{2y} - w = 0 \ldotp\]
À partir du diagramme du corps libre, les magnitudes des composantes de ces équations sont
\[\begin{split} T_{1x} & = T_{1} \cos \alpha_{1} = \frac{T_{1}}{\sqrt{5}},\quad T_{1y} = T_{1} \sin \alpha_{1} = \frac{2T_{1}}{\sqrt{5}} \\ T_{2x} & = T_{2} \cos \alpha_{2} = \frac{2T_{2}}{\sqrt{5}},\quad T_{2y} = T_{2} \sin \alpha_{2} = \frac{T_{2}}{\sqrt{5}} \ldotp \end{split}\]
Nous remplaçons ces composants dans les conditions d'équilibre et simplifions. Nous obtenons ensuite deux équations d'équilibre pour les tensions :
dans la direction X,\[T_{1} = 2T_{2}\]
dans la direction Y,\[\frac{2T_{1}}{\sqrt{5}} + \frac{T_{2}}{\sqrt{5}} = (M + m)g \ldotp\]
L'équation d'équilibre pour la direction x nous indique que la tension T 1 dans la corde de 5,0 cm est le double de la tension T 2 dans la corde de 10,0 cm. Par conséquent, la chaîne la plus courte se cassera. Lorsque nous utilisons la première équation pour éliminer T 2 de la deuxième équation, nous obtenons la relation entre la masse m sur le plateau et la tension T 1 dans la chaîne la plus courte :
\[\frac{2.5T_{1}}{\sqrt{5}} = (M + m)g \ldotp\]
La corde se brise lorsque la tension atteint la valeur critique de T 1 = 2,80 N. L'équation précédente peut être résolue pour la masse critique m qui brise la corde :
\[m = \frac{2.5}{\sqrt{5}} \frac{T_{1}}{g} - M = \frac{2.5}{\sqrt{5}} \frac{2.80\; N}{9.8\; m/s^{2}} - 0.042\; kg = 0.277\; kg = 277.0\; g \ldotp\]
L'importance
Supposons que le système mécanique considéré dans cet exemple soit fixé à un plafond à l'intérieur d'un ascenseur montant. Tant que l'élévateur monte à une vitesse constante, le résultat reste le même car le poids w ne change pas. Si l'élévateur se déplace vers le haut avec une accélération, la masse critique est plus faible car le poids de M + m augmente d'un poids apparent en raison de l'accélération de l'ascenseur. Néanmoins, dans tous les cas, la chaîne la plus courte se brise en premier.


