4.2 : Vecteurs de déplacement et de vitesse

Last updated
Save as PDF

Page ID: 191527

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

OBJECTIFS D'APPRENTISSAGE

Calculez des vecteurs de position dans un problème de déplacement multidimensionnel.
Résolvez le déplacement en deux ou trois dimensions.
Calculez le vecteur de vitesse en fonction du vecteur de position en fonction du temps.
Calculez la vitesse moyenne dans plusieurs dimensions.

Le déplacement et la vitesse en deux ou trois dimensions sont des extensions simples des définitions unidimensionnelles. Cependant, maintenant, ce sont des quantités vectorielles, donc les calculs avec elles doivent suivre les règles de l'algèbre vectorielle, et non de l'algèbre scalaire.

Vecteur de déplacement

Pour décrire un mouvement en deux et trois dimensions, nous devons d'abord établir un système de coordonnées et une convention pour les axes. Nous utilisons généralement les coordonnées$x$$y$, et$z$ pour localiser une particule à un point$P(x, y, z)$ en trois dimensions. Si la particule se déplace, les variables$x$$y$, et$z$ sont des fonctions du temps ($t$) :

\[x = x(t) \quad y = y(t) \quad z = z(t) \ldotp \label{4.1}\]

Le vecteur de position entre l'origine du système de coordonnées et le point P est$\vec{r}(t)$. Dans la notation vectorielle unitaire, introduite dans Systèmes de coordonnées et composants d'un vecteur,$\vec{r}$ (t) est

\[\vec{r} (t) = x(t)\; \hat{i} + y(t)\; \hat{j} + z(t)\; \hat{k} \ldotp \label{4.2}\]

La figure$\PageIndex{1}$ montre le système de coordonnées et le vecteur jusqu'au point$P$ où une particule pourrait être localisée à un moment donné$t$. Notez l'orientation des axes x, y et z. Cette orientation est appelée système de coordonnées pour la main droite et elle est utilisée tout au long du chapitre.

Un système de coordonnées x y z est affiché, avec un x positif hors de la page, un y positif vers la droite et un z positif vers le haut. Un point P, dont les coordonnées x de t, y de t et z de t est indiqué. Toutes les coordonnées de P sont positives. Le vecteur r de t depuis l'origine jusqu'à P est également représenté par une flèche violette. Les coordonnées x de t, y de t et z de t sont affichées sous forme de lignes pointillées. X de t est un segment dans le plan x y, parallèle à l'axe x, y de t est un segment dans le plan x y, parallèle à l'axe y, et z de t est un segment parallèle à l'axe z. — Figure$\PageIndex{1}$ : Système de coordonnées tridimensionnel avec une particule en position$P(x(t), y(t), z(t))$.

Avec notre définition de la position d'une particule dans un espace tridimensionnel, nous pouvons formuler le déplacement tridimensionnel. La figure$\PageIndex{3}$ montre une particule à l'instant t ₁ située à P ₁ avec le vecteur de position$\vec{r}$ (t ₁). À un instant t ₂ ultérieur, la particule est localisée en P ₂ avec le vecteur de position$\vec{r}$ (t ₂). Le vecteur de déplacement$\Delta \vec{r}$ est obtenu en soustrayant$\vec{r}(t_1)$ à$\vec{r}(t_2)$ :

\[\Delta \vec{r} = \vec{r} (t_{2}) - \vec{r} (t_{1}) \ldotp \label{4.3}\]

L'ajout de vecteurs est abordé dans Vecteurs. Notez qu'il s'agit de la même opération que nous avons faite dans une dimension, mais maintenant les vecteurs se trouvent dans un espace tridimensionnel.

Un système de coordonnées x y z est affiché, avec un x positif hors de la page, un y positif vers la droite et un z positif vers le haut. Deux points, P 1 et P 2 sont représentés. Le vecteur r de t 1 depuis l'origine vers P 1 et le vecteur r de t 2 depuis l'origine vers P 2 sont représentés par des flèches violettes. Le vecteur delta r est représenté par une flèche violette dont la queue est en P 1 et la tête en P 2. — Figure$\PageIndex{2}$ : Le déplacement$\Delta \vec{r} = \vec{r}(t_2) − \vec{r}(t_1)$ est le vecteur de$P_1$ à$P_2$.

Les exemples suivants illustrent le concept de déplacement en plusieurs dimensions

Exemple 4.1 : Satellite en orbite polaire

Un satellite se trouve sur une orbite polaire circulaire autour de la Terre à une altitude de 400 km, ce qui signifie qu'il passe directement au-dessus des pôles Nord et Sud. Quelles sont l'amplitude et la direction du vecteur de déplacement entre le moment où il se trouve directement au-dessus du pôle Nord et le moment où il se trouve à −45° de latitude ?

Stratégie

Nous faisons une image du problème pour visualiser graphiquement la solution. Cela nous aidera à mieux comprendre le déplacement. Nous utilisons ensuite des vecteurs unitaires pour résoudre le déplacement.

Solution

La figure$\PageIndex{3}$ montre la surface de la Terre et un cercle qui représente l'orbite du satellite. Bien que les satellites se déplacent dans un espace tridimensionnel, ils suivent des trajectoires d'ellipses, qui peuvent être représentées graphiquement en deux dimensions. Les vecteurs de position sont tracés à partir du centre de la Terre, que nous considérons comme l'origine du système de coordonnées, avec l'axe Y au nord et l'axe des abscisses à l'est. Le vecteur entre eux est le déplacement du satellite. Nous prenons le rayon de la Terre comme étant de 6370 km, donc la longueur de chaque vecteur de position est de 6770 km.

Un système de coordonnées x y, centré sur la Terre, est affiché. Un x positif est à l'est et un y positif au nord. Un cercle bleu plus grand et concentrique à la Terre est représenté. Le vecteur r de t 1 est une flèche orange allant de l'origine à l'endroit où le cercle bleu croise l'axe y (90 degrés dans le sens inverse des aiguilles d'une montre à partir de l'axe x positif). Le vecteur r de t 2 est une flèche orange allant de l'origine à l'emplacement sur le cercle bleu à moins 45 degrés. Le vecteur delta r est représenté par une flèche violette pointant vers le bas et vers la droite, commençant à la tête du vecteur r de t 1 et se terminant à la tête du vecteur r de t 2. — Figure$\PageIndex{3}$ : Deux vecteurs de position sont tracés à partir du centre de la Terre, qui est l'origine du système de coordonnées, avec l'axe Y au nord et l'axe des abscisses à l'est. Le vecteur entre eux est le déplacement du satellite.

En notation vectorielle unitaire, les vecteurs de position sont

\[ \begin{align*} \vec{r}(t_{1}) &= 6770 \ldotp \; km\; \hat{j} \\[4pt] \vec{r}(t_{2}) &= 6770 \ldotp \; km (\cos (-45°))\; \hat{i} + 6770 \ldotp \; km (\sin(−45°))\; \hat{j} \ldotp \end{align*}\]

En évaluant le sinus et le cosinus, nous avons

\[ \begin{align*} \vec{r}(t_{1}) &= 6770 \ldotp \hat{j} \\[4pt] \vec{r}(t_{2}) &= 4787\; \hat{i} − 4787\; \hat{j} \ldotp \end{align*}\]

Nous pouvons maintenant trouver$\Delta \vec{r}$ le déplacement du satellite :

\[\Delta \vec{r} = \vec{r} (t_{2}) - \vec{r} (t_{1}) = 4787\; \hat{i} - 11,557\; \hat{j} \ldotp \nonumber\]

L'ampleur du déplacement est

\[|\Delta \vec{r}| = \sqrt{(4787)^{2} + (-11,557)^{2}} = 12,509\; km. \nonumber\]

L'angle que fait le déplacement avec l'axe X est

\[\theta = \tan^{-1} \left(\dfrac{-11,557}{4787}\right) = -67.5^{o} \nonumber.\]

L'importance

Le tracé du déplacement donne des informations et une signification à la solution vectorielle unitaire au problème. Lorsque vous tracez le déplacement, nous devons inclure ses composantes ainsi que sa magnitude et l'angle qu'il fait avec un axe choisi, dans ce cas, l'axe X (Figure$\PageIndex{4}$).

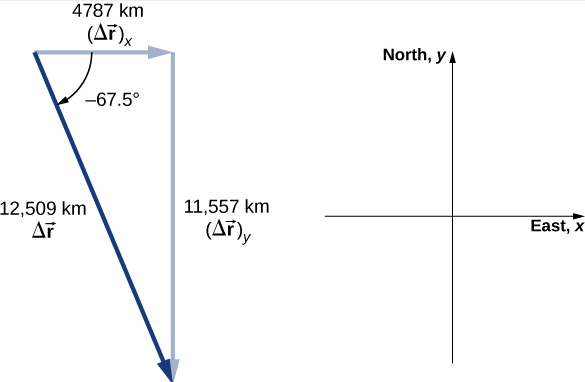
Un système de coordonnées x y est affiché. Un x positif est à l'est et un y positif au nord. Le vecteur delta r sub x pointe vers l'est et a une magnitude de 4787 kilomètres. Le vecteur delta r sub y pointe vers le sud et a une magnitude de 11 557 kilomètres. Le vecteur delta r pointe vers le sud-est, commençant à la queue du delta r sub x et se terminant à la tête du delta r sub y et a une magnitude de 12 509 kilomètres. — Figure$\PageIndex{4}$ : Vecteur de déplacement avec composantes, angle et amplitude.

Notez que le satellite a suivi une trajectoire courbe le long de son orbite circulaire pour passer de sa position initiale à sa position finale dans cet exemple. Il aurait également pu parcourir 4787 km à l'est, puis 11 557 km vers le sud pour arriver au même endroit. Ces deux trajectoires sont plus longues que la longueur du vecteur de déplacement. En fait, le vecteur de déplacement donne le chemin le plus court entre deux points en une, deux ou trois dimensions.

De nombreuses applications en physique peuvent avoir une série de déplacements, comme indiqué dans le chapitre précédent. Le déplacement total est la somme des déplacements individuels, mais cette fois, nous devons faire attention, car nous ajoutons des vecteurs. Nous illustrons ce concept par un exemple de mouvement brownien.

Exemple 4.2 : mouvement brownien

Le mouvement brownien est un mouvement aléatoire chaotique de particules en suspension dans un fluide, résultant de collisions avec les molécules du fluide. Ce mouvement est tridimensionnel. Les déplacements par ordre numérique d'une particule soumise à un mouvement brownien peuvent ressembler à ce qui suit, en micromètres (Figure$\PageIndex{5}$) :

\[\Delta \vec{r}_{1} = 2.0\; \hat{i} + \hat{j} + 3.0 \hat{k}\]

\[\Delta \vec{r}_{2} = - \hat{i} + 3.0\; \hat{k}\]

\[\Delta \vec{r}_{3} = 4.0\; \hat{i} -2.0\; \hat{j} + \hat{k}\]

\[\Delta \vec{r}_{4} = -3.0\; \hat{i} + \hat{j} + 3.0\; \hat{k} \ldotp\]

Quel est le déplacement total de la particule par rapport à son origine ?

Un système de coordonnées x y z avec des distances mesurées en micromètres et comprises entre -10 et +10 micromètres est illustré. Les déplacements delta r sub 1 sont égaux à 2 I hat plus j hat plus 2 k hat, delta r sub 2 est égal à -1 I hat plus 3 k hat, et delta r sub 3 est égal à -3 I hat plus j hat plus 2 k hat sont représentés par des segments de ligne bleue. Vecteur r 1 qui part de l'origine. Chaque déplacement suivant commence là où se termine le précédent. Le vecteur delta r total est représenté par une ligne rouge commençant à l'origine et se terminant à la fin du vecteur delta r 4. Le delta ou le total est égal à 2 K plus 0 Y plus 9 k chapeau. — Figure$\PageIndex{5}$ : Trajectoire d'une particule subissant des déplacements aléatoires du mouvement brownien. Le déplacement total est indiqué en rouge.

Solution

Nous formons la somme des déplacements et les ajoutons sous forme de vecteurs :

\[\begin{split} \Delta \vec{r}_{Total} & = \sum \Delta \vec{r}_{i} = \Delta \vec{r}_{1} + \Delta \vec{r}_{2} + \Delta \vec{r}_{3} + \Delta \vec{r}_{4} \\ & = (2.0 - 1.0 + 4.0 - 3.0)\; \hat{i} + (1.0 + 0 - 2.0 + 1.0)\; \hat{j} + (3.0 +3.0 + 1.0 + 2.0)\; \hat{k} \\ & = 2.0\; \hat{i} + 0\; \hat{j} + 9.0\; \hat{k}\; \mu m \ldotp \end{split}\]

Pour compléter la solution, nous exprimons le déplacement sous la forme d'une amplitude et d'une direction,

\[| \Delta \vec{r}_{Total}| = \sqrt{2.0^{2} + 0^{2} + 9.0^{2}} = 9.2 \mu m, \quad \theta = \tan^{-1} \left(\dfrac{9}{2}\right) = 77^{o},\]

par rapport à l'axe X dans le plan xz.

L'importance

Sur la figure, nous pouvons voir que l'ampleur du déplacement total est inférieure à la somme des magnitudes des déplacements individuels.

Vecteur de vitesse

Dans le chapitre précédent, nous avons trouvé la vitesse instantanée en calculant la dérivée de la fonction de position par rapport au temps. Nous pouvons faire la même opération en deux et trois dimensions, mais nous utilisons des vecteurs. Le vecteur de vitesse instantanée est maintenant

\[\vec{v} (t) = \lim_{\Delta t \rightarrow 0} \frac{\vec{r} (t + \Delta t) - \vec{r} (t)}{\Delta t} = \frac{d \vec{r}}{dt} \ldotp \label{4.4}\]

Examinons graphiquement l'orientation relative du vecteur de position et du vecteur de vitesse. Dans la figure,$\PageIndex{6}$ nous montrons les vecteurs$\vec{r}$ (t) et$\vec{r}$ (t +$\Delta$ t), qui donnent la position d'une particule se déplaçant le long d'une trajectoire représentée par la ligne grise. Lorsque$\Delta$ t passe à zéro, le vecteur de vitesse, donné par l'équation \ ref {4.4}, devient tangent à la trajectoire de la particule au temps t.

Les vecteurs r de t et r de t plus delta t sont représentés par des flèches rouges dans le système de coordonnées x y. Les deux vecteurs commencent à l'origine. Le vecteur delta r pointe de la tête du vecteur r de t vers la tête du vecteur r de t plus delta t. — Figure$\PageIndex{6}$ : Une particule se déplace le long d'une trajectoire indiquée par la ligne grise. Dans la limite, lorsque$\Delta$ t approche zéro, le vecteur de vitesse devient tangent à la trajectoire de la particule.

L'équation \ ref {4.4} peut également être écrite en termes de composantes de$\vec{v}$ (t). Depuis

\[\vec{r} (t) = x(t)\; \hat{i} + y(t)\; \hat{j} + z(t)\; \hat{k},\]

nous pouvons écrire

\[\vec{v} (t) = v_{x} (t)\; \hat{i} + v_{y} (t)\; \hat{j} + v_{z} (t)\; \hat{k} \label{4.5}\]

où

\[v_{x} (t) = \frac{dx(t)}{dt}, \quad v_{y} (t) = \frac{dy(t)}{dt}, \quad v_{z} (t) = \frac{dz(t)}{dt} \ldotp \label{4.6}\]

Si seule la vitesse moyenne est préoccupante, nous avons l'équivalent vectoriel de la vitesse moyenne unidimensionnelle pour deux et trois dimensions :

\[\vec{v}_{avg} = \frac{\vec{r} (t_{2}) - \vec{r} (t_{1})}{t_{2} - t_{1}} \ldotp \label{4.7}\]

Exemple 4.3 : Calcul du vecteur de vitesse

La fonction de position d'une particule est$\vec{r}$ (t) = 2,0 t ²$\hat{i}$ + (2,0 + 3,0 t)$\hat{j}$ + 5,0 t$\hat{k}$ m. (a) Quelles sont la vitesse et la vitesse instantanées à t = 2,0 s ? (b) Quelle est la vitesse moyenne entre 1,0 s et 3,0 s ?

Solution

En utilisant l'équation \ ref {4.5} et l'équation \ ref {4.6}, et en prenant la dérivée de la fonction de position par rapport au temps, nous trouvons

$$v (t) = \ frac {d \ vec {r} (t)} {dt} = 4,0t \ ; \ hat {i} + 3,0 \ ; \ chapeau {j} + 5,0 \ ; \ chapeau {k} \ ; m/s$$$ \ vec {v} (2,0 \ ; s) = 8,0 \ ; \ chapeau {i} + 3,0 \ ; \ chapeau {j} + 5,0 \ ; \ hat {k} \ ; M/S$$$$Vitesse \ ; | \ vec {v} (2,0 \ ; s) | = \ sqrt {8^ {2} + 3^ {2} + 5^ {2}} = 9,9 \ ; m/s \ ldotp$$
À partir de l'équation \ ref {4.7}, $$ \ begin {split} \ vec {v} _ {avg} & = \ frac {\ vec {r} (t_ {2}) - \ vec {r} (t_ {1})} {t_ {2} - t_ {1}} = \ frac {\ vec {r} (3,0 \ ; s) - \ {vec {r} r} (1,0 \ ; s)} {3,0 \ ; s - 1,0 \ ; s} = \ frac {(18 \ ; \ hat {i} + 11 \ ; \ chapeau {j} + 15 \ ; \ chapeau {k}) m - (2 \ ; \ chapeau {i} + 5 \ ; \ chapeau {j} + 5 \ ; \ chapeau {k}) m} {2,0 \ ; s} \ \ & \ frac {( 16 \ ; \ hat {i} + 6 \ ; \ chapeau {j} + 10 \ ; \ chapeau {k}) m} {2,0 \ ; s} = 8,0 \ ; \ chapeau {i} + 3,0 \ ; \ chapeau {j} + 5,0 \ ; \ chapeau {k} \ ; m/s \ ldotp \ end {split} $$

L'importance

Nous voyons que la vitesse moyenne est la même que la vitesse instantanée à t = 2,0 s, du fait que la fonction de vitesse est linéaire. Cela ne doit pas nécessairement être le cas en général. En fait, la plupart du temps, les vitesses instantanées et moyennes ne sont pas les mêmes.

Exercice 4.1

La fonction de position d'une particule est$\vec{r}$ (t) = 3,0t ³$\hat{i}$ + 4,0$\hat{j}$. (a) Quelle est la vitesse instantanée à t = 3 s ? (b) La vitesse moyenne entre 2 s et 4 s est-elle égale à la vitesse instantanée à t = 3 s ?

L'indépendance des mouvements perpendiculaires

Lorsque nous examinons les équations tridimensionnelles de position et de vitesse écrites en notation vectorielle unitaire, Équation \ ref {4.2} et Équation \ ref {4.5}, nous voyons que les composantes de ces équations sont des fonctions distinctes et uniques du temps qui ne dépendent pas les unes des autres. Le mouvement le long de la direction x n'a aucune part de son mouvement le long des directions y et z, et il en va de même pour les deux autres axes de coordonnées. Ainsi, le mouvement d'un objet en deux ou trois dimensions peut être divisé en mouvements distincts et indépendants le long des axes perpendiculaires du système de coordonnées dans lequel le mouvement a lieu.

Pour illustrer ce concept en ce qui concerne le déplacement, imaginez une femme marchant d'un point A à un point B dans une ville aux pâtés de maisons carrées. La femme qui emprunte le chemin d'un point A à un point B peut marcher vers l'est sur de nombreux pâtés de maisons, puis vers le nord (deux directions perpendiculaires) pour atteindre B. Seul son mouvement vers l'est influe sur la distance qu'elle parcourt vers l'est. De même, la distance qu'elle parcourt vers le nord n'est affectée que par son mouvement vers le nord.

Indépendance du mouvement

Dans la description cinématique du mouvement, nous sommes en mesure de traiter séparément les composantes horizontale et verticale du mouvement. Dans de nombreux cas, le mouvement dans le sens horizontal n'affecte pas le mouvement dans le sens vertical, et vice versa.

Un exemple illustrant l'indépendance des mouvements verticaux et horizontaux est donné par deux balles de baseball. Une balle de baseball est retirée du repos. Au même instant, un autre est projeté horizontalement de la même hauteur et suit une trajectoire courbe. Un stroboscope saisit la position des balles à intervalles de temps fixes lorsqu'elles tombent (Figure$\PageIndex{7}$).

Deux balles identiques sont illustrées à 5 endroits à intervalles de temps égaux. Les balles commencent à la même position verticale. Les flèches vertes représentent les vitesses horizontales et les flèches violettes représentent les vitesses verticales à chaque position. La balle de droite a une vitesse horizontale initiale alors que la balle de gauche n'a aucune vitesse horizontale. Le mouvement horizontal est une vitesse horizontale constante à tout moment pour les deux balles. Le mouvement vertical est une accélération verticale constante. La vitesse verticale de chaque balle augmente en amplitude et pointe vers le bas. À chaque instant, les deux balles ont des positions verticales et des vitesses verticales identiques. — Figure$\PageIndex{7}$ : Schéma des mouvements de deux balles identiques : l'une tombe du repos et l'autre a une vitesse horizontale initiale. Chaque position suivante correspond à un intervalle de temps égal. Les flèches représentent les vitesses horizontale et verticale à chaque position. La balle de droite a une vitesse horizontale initiale alors que la balle de gauche n'a aucune vitesse horizontale. Malgré la différence de vitesse horizontale, les vitesses et positions verticales sont identiques pour les deux balles, ce qui montre que les mouvements verticaux et horizontaux sont indépendants.

Il est remarquable que pour chaque flash du stroboscope, les positions verticales des deux boules soient les mêmes. Cette similitude implique que le mouvement vertical est indépendant du fait que la balle se déplace horizontalement ou non. (En supposant l'absence de résistance de l'air, le mouvement vertical d'un objet qui tombe est influencé uniquement par la gravité, et non par des forces horizontales.) Un examen attentif de la balle lancée horizontalement montre qu'elle parcourt la même distance horizontale entre les éclairs. En effet, il n'y a aucune force supplémentaire sur la balle dans le sens horizontal après son lancement. Ce résultat signifie que la vitesse horizontale est constante et n'est affectée ni par le mouvement vertical ni par la gravité (qui est verticale). Notez que ce cas n'est vrai que dans des conditions idéales. Dans le monde réel, la résistance de l'air affecte la vitesse des balles dans les deux sens.

La trajectoire incurvée bidimensionnelle de la balle lancée horizontalement est composée de deux mouvements unidimensionnels indépendants (horizontal et vertical). La clé pour analyser un tel mouvement, appelé mouvement du projectile, est de le résoudre en mouvements dans des directions perpendiculaires. La résolution d'un mouvement bidimensionnel en composants perpendiculaires est possible car les composants sont indépendants.