16.3 : Ondes électromagnétiques planes
- Page ID
- 191204
À la fin de cette section, vous serez en mesure de :
- Décrire comment les équations de Maxwell prédisent les directions relatives des champs électriques et magnétiques, ainsi que la direction de propagation des ondes électromagnétiques planes
- Expliquez comment les équations de Maxwell prédisent que la vitesse de propagation des ondes électromagnétiques dans l'espace libre est exactement la vitesse de la lumière
- Calculer l'amplitude relative des champs électriques et magnétiques dans une onde plane électromagnétique
- Décrire comment les ondes électromagnétiques sont produites et détectées
Les ondes mécaniques traversent un milieu tel qu'une ficelle, de l'eau ou de l'air. La prédiction la plus significative des équations de Maxwell est peut-être l'existence de champs électriques et magnétiques (ou électromagnétiques) combinés qui se propagent dans l'espace sous forme d'ondes électromagnétiques. Comme les équations de Maxwell s'appliquent à l'espace libre, les ondes électromagnétiques prédites, contrairement aux ondes mécaniques, ne nécessitent pas de milieu pour se propager.
Un traitement général de la physique des ondes électromagnétiques n'entre pas dans le cadre de ce manuel. Nous pouvons cependant étudier le cas particulier d'une onde électromagnétique qui se propage dans l'espace libre le long de l'axe x d'un système de coordonnées donné.
Ondes électromagnétiques dans une direction
Une onde électromagnétique est constituée d'un champ électrique, défini comme d'habitude en termes de force par charge sur une charge stationnaire, et d'un champ magnétique, défini en termes de force par charge sur une charge mobile. Le champ électromagnétique est supposé être fonction uniquement de la coordonnée x et du temps. La composante y du champ électrique s'écrit alors\(E_y (x,t)\), la composante z du champ magnétique comme, etc. Comme nous supposons de l'espace libre\(B_z (x,t)\), il n'y a pas de charges ni de courants libres, donc nous pouvons définir\(Q_{in} = 0\) et\(I = 0\) dans les équations de Maxwell.
La nature transversale des ondes électromagnétiques
Nous examinons d'abord ce que la loi de Gauss pour les champs électriques implique concernant les directions relatives du champ électrique et la direction de propagation dans une onde électromagnétique. Supposons que la surface gaussienne est la surface d'une boîte rectangulaire dont la section transversale est un carré du côté l et dont le troisième côté a une longueur\(\Delta x\), comme le montre la figure\(\PageIndex{1}\). Comme le champ électrique est fonction uniquement de x et de t, la composante y du champ électrique est la même en haut (étiqueté côté 2) et en bas (côté 1) de la boîte, de sorte que ces deux contributions au flux s'annulent. L'argument correspondant vaut également pour le flux net provenant de la composante z du champ électrique à travers les côtés 3 et 4. Tout flux net à travers la surface provient donc entièrement de la composante x du champ électrique. Parce que le champ électrique ne dépend pas de y ou de z, qu'\(E_x(x,t)\)il est constant sur la face de la boîte de surface A et qu'il a une valeur éventuellement différente\(E_x (x + \Delta x, t)\) qui est constante sur la face opposée de la boîte.
L'application de la loi de Gauss donne
\[\text{Net flux} = - E_x (x,t) A + E_x (x + \Delta x, t) A = \dfrac{Q_{in}}{\epsilon_0} \label{16.13}\]
où\(A = l \times l\) est la surface des faces avant et arrière de la surface rectangulaire. Mais la charge incluse l'est\(Q_{in} = 0\), donc le flux net de ce composant est également nul, et l'équation \ ref {16.13} implique\(E_x (x,t) = E_x (x + \Delta x, t)\) pour tout\(\Delta x\). Par conséquent, s'il existe une composante x du champ électrique, elle ne peut pas varier avec x. Un tel champ uniforme serait simplement superposé artificiellement à l'onde progressive, par exemple en ayant une paire de plaques chargées en parallèle. Un tel composant ne\(E_x(x,t)\) ferait pas partie d'une onde électromagnétique se propageant le long de l'axe x ; il en va de même\(E_x(x,t) = 0\) pour cette onde. Par conséquent, les seules composantes non nulles du champ électrique sont\(E_y(x,t)\) et\(E_z(x,t)\) perpendiculaires à la direction de propagation de l'onde.
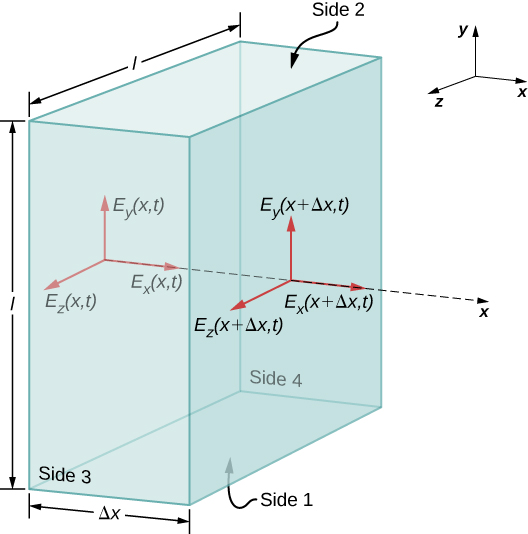
A similar argument holds by substituting E for B and using Gauss’s law for magnetism instead of Gauss’s law for electric fields. This shows that the B field is also perpendicular to the direction of propagation of the wave. The electromagnetic wave is therefore a transverse wave, with its oscillating electric and magnetic fields perpendicular to its direction of propagation.
The speed of propagation of electromagnetic waves
We can next apply Maxwell’s equations to the description given in connection with Figure 16.2.3 in the previous section to obtain an equation for the E field from the changing B field, and for the B field from a changing E field. We then combine the two equations to show how the changing E and B fields propagate through space at a speed precisely equal to the speed of light.
First, we apply Faraday’s law over Side 3 of the Gaussian surface, using the path shown in Figure \(\PageIndex{2}\). Because \(E_x(x,t) = 0\), we have
\[\oint \vec{E} \cdot d\vec{s} = - E_y(x,t)l + E_y(x + \Delta x,t)l.\]
Assuming \(\Delta x\) is small and approximating \(E_y (x + \Delta x,t)\) by
\[E_y (x + \Delta x,t) = E_y (x,t) + \dfrac{\partial E_y(x,t)}{\partial x} \Delta x,\]
we obtain
\[\oint \vec{E} \cdot d\vec{s} = \dfrac{\partial E_y (x,t)}{\partial x} (l\Delta x).\]
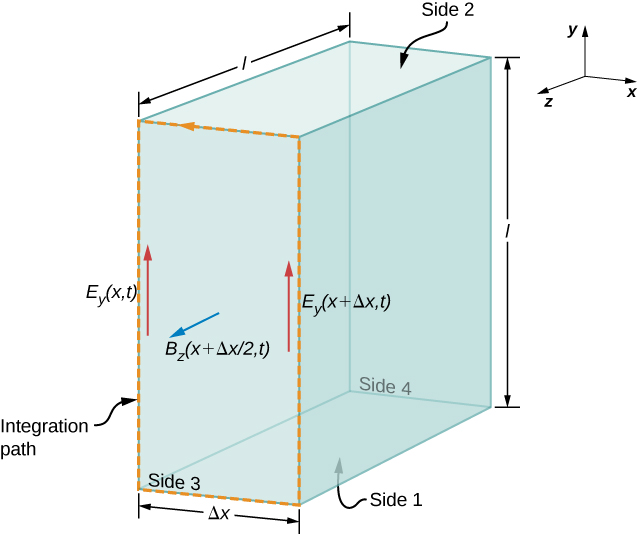
Comme\(\Delta x\) il est faible, le flux magnétique à travers la face peut être approximé par sa valeur au centre de la zone parcourue, à savoir\(B_z\left(x + \dfrac{\Delta x}{2}, t\right)\). Le flux du champ B à travers la face 3 est alors le champ B multiplié par la surface,
\[\oint_S \vec{B} \cdot \vec{n} dA = B_z \left(x + \dfrac{\Delta x}{2}, t\right) (l \Delta x). \label{16.14}\]
\[\oint \vec{E} \cdot d\vec{s} = -\dfrac{d}{dt} \int_S \vec{B} \cdot \vec{n} dA.\label{16.15}\]
Par conséquent, à partir des équations \ ref {16.13} et \ ref {16.14},
\[\dfrac{\partial E_y (x,t)}{\partial x} (l \Delta x) = - \dfrac{\partial}{\partial t} \left[ B_z \left( x + \dfrac{\Delta x}{2}, t\right) \right] (l\Delta x).\]
Annulation\(l \Delta x\) et prise de la limite au fur\(\Delta x = 0\) et à mesure qu'il nous reste
\[\dfrac{\partial E_y (x,t)}{\partial x} = - \dfrac{\partial B_z(x,t)}{\partial t}. \label{16.16}\]
Nous aurions plutôt pu appliquer la loi de Faraday à la surface supérieure (numérotée 2) de la Figure\(\PageIndex{2}\), pour obtenir l'équation résultante
\[\dfrac{\partial B_z(x,t)}{\partial t} = - \dfrac{\partial E_y (x,t)}{\partial x}. \label{16.17}\]
Il s'agit de l'équation décrivant le champ E dépendant de l'espace produit par le champ B dépendant du temps.
Ensuite, nous appliquons la loi Ampère-Maxwell (avec\(I = 0\)) sur les deux mêmes faces (Surface 3 puis Surface 2) de la boîte rectangulaire de la Figure\(\PageIndex{2}\). En appliquant l'équation 16.2.16,
\[\oint \vec{B} \cdot d\vec{s} = \mu_0 \epsilon_0 (d/dt) \int_S \vec{E} \cdot n \, da\]
à la surface 3, puis à la surface 2, donne les deux équations
\[\dfrac{\partial E_y (x,t)}{\partial x} = - \epsilon_0 \mu_0 \dfrac{\partial E_z (x,t)}{\partial t}, \label{16.18}\]
et
\[\dfrac{\partial B_z(x,t)}{\partial x} = - \epsilon_0 \mu_0 \dfrac{\partial E_y (x,t)}{\partial t}. \label{16.19}\]
Ces équations décrivent le champ B dépendant de l'espace produit par le champ E dépendant du temps.
Nous combinons ensuite les équations montrant le champ B changeant produisant un champ E avec l'équation montrant le champ E changeant produisant un champ B. En prenant la dérivée de l'équation \ ref {16.16} par rapport à x et en utilisant l'équation \ ref {16.26}, on obtient
\[\dfrac{\partial^2E_y}{\partial x^2} = \dfrac{\partial}{\partial x}\left(\dfrac{\partial E_y}{\partial x}\right) = - \dfrac{\partial}{\partial x}\left(\dfrac{\partial B_z}{\partial t}\right) = - \dfrac{\partial}{\partial t}\left(\dfrac{\partial B_z}{\partial x}\right) = \dfrac{\partial}{\partial t}\left(\epsilon_0 \mu_0 \dfrac{\partial E_y}{\partial t}\right)\]
ou
\[\dfrac{\partial^2E_y}{\partial x^2} = \epsilon_0 \mu_0 \dfrac{\partial^2 E_y}{\partial t^2}\]
C'est la forme que prend l'équation générale des vagues pour notre onde plane. Comme les équations décrivent une onde se déplaçant à une vitesse c encore non spécifiée, nous pouvons supposer que les composantes du champ sont chacune des fonctions de x — ct pour l'onde se déplaçant dans la direction + x, c'est-à-dire
\[E_y (x,t) = f(\xi) \, where \, \xi = x - ct. \label{16.21}\]
Il s'agit d'un exercice mathématique pour montrer, en utilisant la règle de la chaîne pour la différenciation, que les équations \ ref {16.17} et \ ref {16.18} impliquent
\[1 = \epsilon_0 \mu_0 c^2.\]
La vitesse de l'onde électromagnétique dans l'espace libre est donc donnée en termes de perméabilité et de permittivité de l'espace libre par
\[c = \dfrac{1}{\sqrt{\epsilon_0\mu_0}}. \label{16.22}\]
Nous aurions tout aussi bien pu supposer une onde électromagnétique avec des composantes de champ\(E_z (x,t)\) et\(B_y (x,t)\). Le même type d'analyse avec l'équation \ ref {16.25} et \ ref {16.24} montrerait également que la vitesse d'une onde électromagnétique est de\(c = 1/\sqrt{\epsilon_0\mu_0}\).
La physique des champs électromagnétiques itinérants a été élaborée par Maxwell en 1873. Il a montré d'une manière plus générale que notre dérivation que les ondes électromagnétiques se déplacent toujours dans l'espace libre à une vitesse donnée par l'équation \ ref {16.18}. Si nous évaluons la vitesse\(c = \dfrac{1}{\sqrt{\epsilon_0\mu_0}}\), nous constatons que
\[c = \dfrac{1}{\sqrt{\left(8.85 \times 10^{-12} \dfrac{C^2}{N \cdot m^2}\right)\left(4\pi \times 10^{-7} \dfrac{T \cdot m}{A}\right)}} = 3.00 \times 10^8 m/s,\]
qui est la vitesse de la lumière. Imaginez l'excitation que Maxwell a dû ressentir lorsqu'il a découvert cette équation ! Il avait découvert un lien fondamental entre deux phénomènes apparemment indépendants : les champs électromagnétiques et la lumière.
L'équation d'onde a été obtenue en (1) trouvant le champ E produit par le champ B changeant, (2) en trouvant le champ B produit par le champ E changeant et en combinant les deux résultats. Laquelle des équations de Maxwell était à la base de l'étape (1) et laquelle de l'étape (2) ?
- Réponse (étape 1)
-
Loi de Faraday
- Réponse (étape 2)
-
la loi Ampère-Maxwell
Comment les champs E et B sont-ils liés
Jusqu'à présent, nous avons vu que les taux de variation des différentes composantes des champs E et B sont liés, que l'onde électromagnétique est transversale et que l'onde se propage à la vitesse c. Nous montrons ensuite ce que les équations de Maxwell impliquent sur le rapport entre les magnitudes des champs E et B et les directions relatives des champs E et B.
Nous examinons maintenant les solutions à l'équation \ ref {16.16} sous forme d'ondes planes pour le champ électrique :
\[E_y(x,t) = E_0 \, \cos \, (kx - \omega t). \label{16.23}\]
Nous avons pris arbitrairement l'onde pour qu'elle se déplace dans la direction +x et avons choisi sa phase de telle sorte que l'intensité de champ maximale se produise à l'origine à un moment donné\(t = 0\). Nous avons raison de ne considérer que les sinus et les cosinus de cette manière et de généraliser les résultats, car le théorème de Fourier implique que nous pouvons exprimer n'importe quelle onde, y compris même les fonctions de pas carrés, comme une superposition de sinus et de cosinus.
À n'importe quel point spécifique de l'espace, le champ E oscille de manière sinusoïdale à une fréquence angulaire\(\omega\) comprise entre\(+E_0\) et\(-E_0\) et et de même, le champ B oscille entre\(+B_0\) et\(-B_0\). L'amplitude de l'onde est la valeur maximale de\(E_y(x,t)\). La période d'oscillation T est le temps nécessaire pour une oscillation complète. La fréquence f est le nombre d'oscillations complètes par unité de temps, et est liée à la fréquence angulaire\(\omega\) par\(\omega = 2\pi f\). La longueur d'onde\(\lambda\) est la distance parcourue par un cycle complet de l'onde, et le nombre d'ondes k est le nombre de longueurs d'onde qui correspondent à une distance de\(2\pi\) dans les unités utilisées. Ces grandeurs sont liées de la même manière que pour une onde mécanique :
\[\omega = 2\pi f, \, \, f = \dfrac{1}{T}, \, \, k = \dfrac{2\pi}{\lambda}, \, \, and \, \, c = f\lambda = \omega/k.\]
Étant donné que la solution de\(E_y\) a la forme indiquée dans l'équation \ ref {16.20}, nous devons déterminer le\(B\) champ qui l'accompagne. À partir de l'équation \ ref {16.24}, la composante du champ magnétique\(B_z\) doit obéir
\[\dfrac{\partial B_z}{\partial t} = - \dfrac{\partial E_y}{\partial x}\]
\[\dfrac{\partial B_z}{\partial t} = - \dfrac{\partial}{\partial x} E_0 \, \cos \, (kx - \omega t) = kE_0 \, sin\, (kx - \omega t). \label{16.24}\]
Comme la solution pour le motif de champ B de l'onde se propage dans la direction + x à la même vitesse c que le motif de champ E, elle doit être fonction de\(k(x - ct) = kx - \omega t\). Ainsi, nous concluons de l'équation \ ref {16.21}\(B_z\) que
\[B_z(x,t) = \dfrac{k}{\omega} E_0 \, \cos \, (kx - \omega t) = \dfrac{1}{c}E_0 \, \cos \, (kx - \omega t).\]
Ces résultats peuvent être écrits sous la forme
\[E_y(x,t) = E_0 \, \cos \, (kx - \omega t)\]
\[B_z(x,t) = B_0 \, \cos \, (kx - \omega t) \label{16.25}\]
\[\dfrac{E_y}{B_z} = \dfrac{E_0}{B_0} = c. \label{16.26}\]
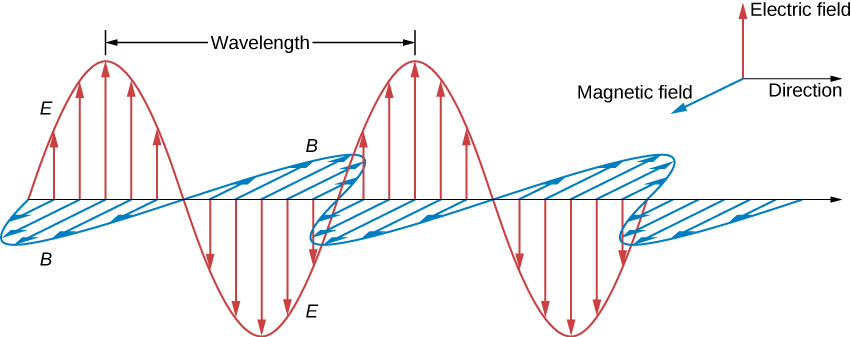
Par conséquent, les pics des champs E et B coïncident, de même que les creux de l'onde, et en chaque point, les champs E et B sont dans le même rapport égal à la vitesse de la lumière c. L'onde plane a la forme illustrée sur la figure\(\PageIndex{3}\).
What is the maximum strength of the B field in an electromagnetic wave that has a maximum E-field strength of 1000 V/m?
Strategy
To find the B-field strength, we rearrange Equation \ref{16.23} to solve for \(B\), yielding
\[B = \dfrac{E}{c}. \nonumber\]
Solution We are given E, and c is the speed of light. Entering these into the expression for B yields
\[B = \dfrac{1000 \, V/m}{3.00 \times 10^8 \, m/s} = 3.33 \times 10^{-6} T. \nonumber\]
Significance
The B-field strength is less than a tenth of Earth’s admittedly weak magnetic field. This means that a relatively strong electric field of 1000 V/m is accompanied by a relatively weak magnetic field.
Changing electric fields create relatively weak magnetic fields. The combined electric and magnetic fields can be detected in electromagnetic waves, however, by taking advantage of the phenomenon of resonance, as Hertz did. A system with the same natural frequency as the electromagnetic wave can be made to oscillate. All radio and TV receivers use this principle to pick up and then amplify weak electromagnetic waves, while rejecting all others not at their resonant frequency.
What conclusions did our analysis of Maxwell’s equations lead to about these properties of a plane electromagnetic wave:
- the relative directions of wave propagation, of the E field, and of B field,
- the speed of travel of the wave and how the speed depends on frequency, and
- the relative magnitudes of the E and B fields.
- Answer a
-
The directions of wave propagation, of the E field, and of B field are all mutually perpendicular.
- Answer b
-
The speed of the electromagnetic wave is the speed of light \(c = 1/\sqrt{\epsilon_0\mu_0}\) independent of frequency.
- Answer c
-
The ratio of electric and magnetic field amplitudes is \(E/B = c\).
Production and Detection of Electromagnetic Waves
A steady electric current produces a magnetic field that is constant in time and which does not propagate as a wave. Accelerating charges, however, produce electromagnetic waves. An electric charge oscillating up and down, or an alternating current or flow of charge in a conductor, emit radiation at the frequencies of their oscillations. The electromagnetic field of a dipole antenna is shown in Figure \(\PageIndex{4}\). The positive and negative charges on the two conductors are made to reverse at the desired frequency by the output of a transmitter as the power source. The continually changing current accelerates charge in the antenna, and this results in an oscillating electric field a distance away from the antenna. The changing electric fields produce changing magnetic fields that in turn produce changing electric fields, which thereby propagate as electromagnetic waves. The frequency of this radiation is the same as the frequency of the ac source that is accelerating the electrons in the antenna. The two conducting elements of the dipole antenna are commonly straight wires. The total length of the two wires is typically about one-half of the desired wavelength (hence, the alternative name half-wave antenna), because this allows standing waves to be set up and enhances the effectiveness of the radiation.
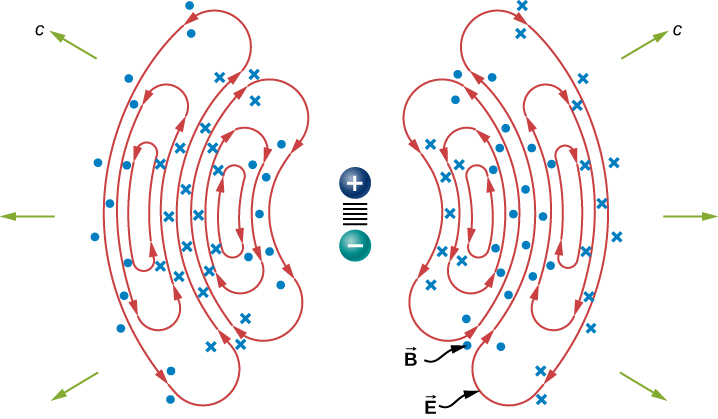
Les lignes de champ électrique dans un plan sont affichées. Le champ magnétique est perpendiculaire à ce plan. Ce champ de rayonnement présente une symétrie cylindrique autour de l'axe du dipôle. Les lignes de champ proches du dipôle ne sont pas représentées. Le motif n'est pas du tout uniforme dans toutes les directions. Le signal le plus fort se trouve dans des directions perpendiculaires à l'axe de l'antenne, qui serait horizontal si l'antenne est montée verticalement. L'intensité est nulle le long de l'axe de l'antenne. Les champs détectés loin de l'antenne proviennent des champs électriques et magnétiques changeants qui s'induisent mutuellement et se propagent sous forme d'ondes électromagnétiques. Loin de l'antenne, les fronts d'ondes, ou surfaces à phase égale pour l'onde électromagnétique, sont presque sphériques. Encore plus loin de l'antenne, le rayonnement se propage comme des ondes électromagnétiques planes.
Les ondes électromagnétiques emportent l'énergie loin de leur source, comme une onde sonore transportant l'énergie d'une onde stationnaire sur une corde de guitare. Une antenne destinée à recevoir des signaux électromagnétiques fonctionne en sens inverse. Les ondes électromagnétiques entrantes induisent des courants oscillants dans l'antenne, chacun à sa propre fréquence. Le récepteur radio comprend un circuit syntoniseur dont la fréquence de résonance peut être ajustée. Le tuner répond fortement à la fréquence souhaitée mais pas aux autres, ce qui permet à l'utilisateur de régler la diffusion souhaitée. Les composants électriques amplifient le signal formé par les électrons en mouvement. Le signal est ensuite converti en format audio et/ou vidéo.
Utilisez cette simulation pour diffuser des ondes radio. Faites bouger l'électron de l'émetteur manuellement ou faites-le osciller automatiquement. Affichez le champ sous forme de courbe ou de vecteurs. Le diagramme à bandes montre la position des électrons au niveau de l'émetteur et du récepteur.


