12.7 : Solénoïdes et toroïdes
- Page ID
- 191053
À la fin de cette section, vous serez en mesure de :
- Établissez une relation entre la façon dont le champ magnétique d'un solénoïde varie en fonction de la distance et du courant en utilisant à la fois la loi de Biot-Savart et la loi d'Ampère
- Établissez une relation entre la façon dont le champ magnétique d'un tore varie en fonction de la distance et du courant en utilisant la loi d'Ampère
Deux des dispositifs électromagnétiques les plus courants et les plus utiles sont appelés solénoïdes et toroïdes. Sous une forme ou une autre, ils font partie de nombreux instruments, grands et petits. Dans cette section, nous examinons le champ magnétique typique de ces appareils.
Solénoïdes
Un long fil enroulé sous la forme d'une bobine hélicoïdale est connu sous le nom de solénoïde. Les solénoïdes sont couramment utilisés dans les recherches expérimentales nécessitant des champs magnétiques. Un solénoïde est généralement facile à enrouler et, près de son centre, son champ magnétique est assez uniforme et directement proportionnel au courant dans le fil.
La figure\(\PageIndex{1}\) montre un solénoïde composé de N spires de fil enroulées étroitement sur une longueur L. Un courant I circule le long du fil du solénoïde. Le nombre de tours par unité de longueur est N/L ; par conséquent, le nombre de tours dans une longueur infinitésimale dy est (N/L) dy tours. Cela produit un courant
\[dI = \frac{NI}{L} dy. \label{12.24}\]
Nous calculons d'abord le champ magnétique au point P de la figure\(\PageIndex{1}\). Ce point se trouve sur l'axe central du solénoïde. Nous découpons essentiellement le solénoïde en fines tranches épaisses et traitons chacune comme une boucle de courant. Ainsi, dI est le courant traversant chaque tranche. Le champ magnétique\(d\vec{B}\) dû au courant dI dans dy peut être déterminé à l'aide de l'équation 12.5.3 et de l'équation \ ref {12.24} :
\[d\vec{B} = \frac{\mu_0 R^2 dI}{2(y^2 + R^2)^{3/2}}\hat{j} = \left( \frac{\mu_0 IR^2 N}{2L}\hat{j}\right) \frac{dy}{(y^2 + R^2)^{3/2}} \label{12.25}\]
où nous avons utilisé l'équation \ ref {12.24} pour remplacer dI. Le champ résultant en P est obtenu en intégrant\(d\vec{B}\) le champ sur toute la longueur du solénoïde. Il est plus facile d'évaluer cette intégrale en remplaçant la variable indépendante de y par\(\theta\). À partir de l'inspection de la figure\(\PageIndex{1}\), nous avons :
\[sin \, \theta = \frac{y}{\sqrt{y^2 + R^2}}.\label{12.26}\]
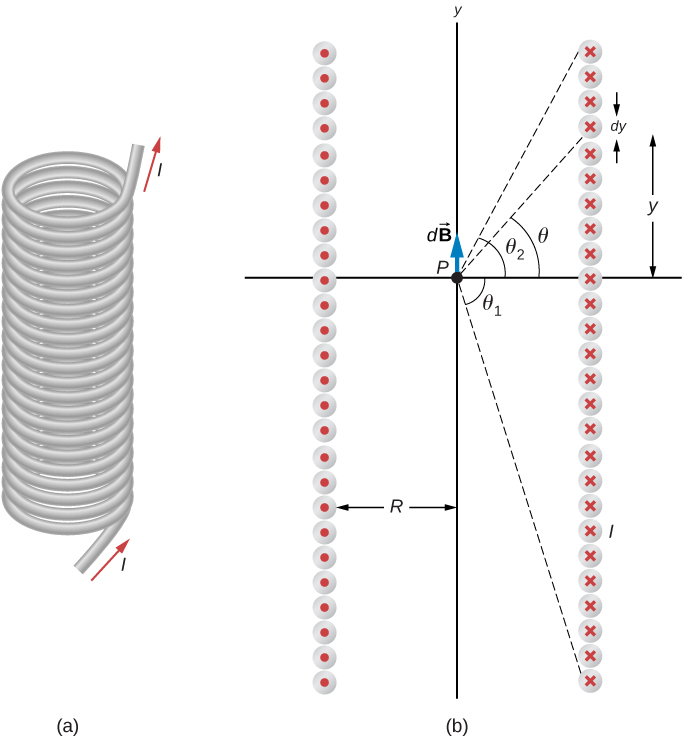
En prenant le différentiel des deux côtés de cette équation, nous obtenons
\[cos \, \theta \, d\theta = \left[ - \frac{y^2}{(y^2 + R^2)^{3/2}} + \frac{1}{\sqrt{y^2 + R^2}}\right] dy \]
\[ = \frac{R^2 dy}{(y^2 + R^2)^{3/2}}.\]
Lorsque cela est remplacé dans l'équation par\(d\vec{B}\), nous avons
\[\vec{B} = \frac{\mu_0 I N}{2L}\hat{j} \int_{\theta_1}^{\theta_2} cos \, \theta \, d\theta = \frac{\mu_0 I N}{2L} (sin \, \theta_2 - sin \, \theta_1)\hat{j}, \label{12.27}\]
qui est le champ magnétique le long de l'axe central d'un solénoïde fini.
Le solénoïde infiniment long, pour lequel, présente un intérêt particulier\(L \rightarrow \infty\). D'un point de vue pratique, le solénoïde infini est un solénoïde dont la longueur est beaucoup plus grande que son rayon\((L >> R)\). Dans ce cas,\(\theta_1 = \frac{-\pi}{2}\) et\(\theta_2 = \frac{\pi}{2}\). Ensuite, à partir de l'équation \ ref {12.27}, le champ magnétique le long de l'axe central d'un solénoïde infini est
\[\vec{B} = \frac{\mu_0 IN}{2L} \hat{j} [sin(\pi/2) - sin(-\pi/2)] = \frac{\mu_0 IN}{L} \hat{j}\]ou
\[\vec{B} = \mu_0 n I \hat{j}, \label{12.28}\]
où n est le nombre de tours par unité de longueur. Vous pouvez trouver la direction de\(\vec{B}\) avec une règle de la main droite : courbez vos doigts dans le sens du courant et votre pouce pointe le long du champ magnétique à l'intérieur du solénoïde.
Nous utilisons maintenant ces propriétés, ainsi que la loi d'Ampère, pour calculer l'amplitude du champ magnétique à n'importe quel endroit à l'intérieur du solénoïde infini. Considérez le chemin fermé de la Figure\(\PageIndex{2}\). Le long du segment 1,\(\vec{B}\) est uniforme et parallèle à la trajectoire. Le long des segments 2 et 4,\(\vec{B}\) est perpendiculaire à une partie du chemin et disparaît sur le reste de celui-ci. Les segments 2 et 4 ne contribuent donc pas à la ligne intégrale de la loi d'Ampère. Le long du segment 3,\(\vec{B} = 0\) car le champ magnétique est nul à l'extérieur du solénoïde. Si vous considérez une boucle de loi d'Ampère à l'extérieur du solénoïde, le courant circule dans des directions opposées sur différents segments de fil. Il n'y a donc pas de courant fermé ni de champ magnétique selon la loi d'Ampère. Il n'y a donc aucune contribution à l'intégrale linéaire à partir du segment 3. Par conséquent, nous trouvons
\[\oint \vec{B} \cdot d\vec{l} = \int_1 \vec{B} \cdot d\vec{l} = Bl. \label{12.29}\]
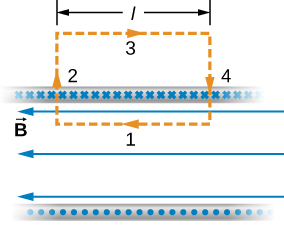
Le solénoïde a n tours par unité de longueur, de sorte que le courant qui traverse la surface entourée par le chemin est NLi. Donc, selon la loi d'Ampère,
\[Bl = \mu_0 n lI\]et
\[B = \mu_0 n I \label{12.30}\]
dans le solénoïde. Cela concorde avec ce que nous avons constaté précédemment pour B sur l'axe central du solénoïde. Ici, cependant, l'emplacement du segment 1 est arbitraire, nous avons donc découvert que cette équation donne le champ magnétique partout à l'intérieur du solénoïde infini.
À l'extérieur du solénoïde, on peut tracer une boucle de loi d'Ampère autour de l'ensemble du solénoïde. Cela engloberait le courant circulant dans les deux sens. Par conséquent, le courant net à l'intérieur de la boucle est nul. Selon la loi d'Ampère, si le courant net est nul, le champ magnétique doit être nul. Par conséquent, pour les emplacements situés en dehors du rayon du solénoïde, le champ magnétique est nul.
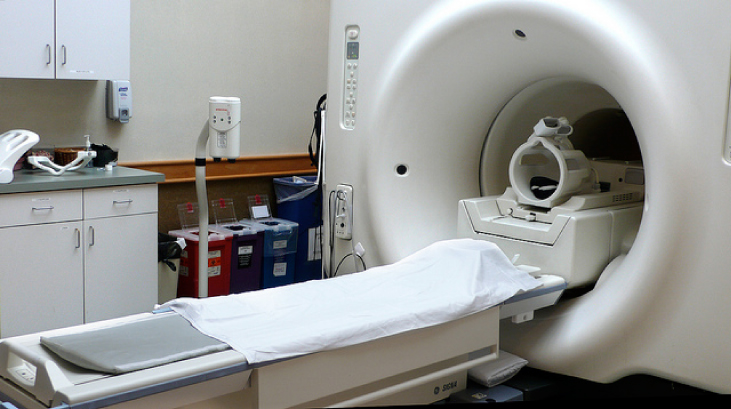
Lorsqu'un patient subit une imagerie par résonance magnétique (IRM), il s'allonge sur une table qui est déplacée au centre d'un gros solénoïde capable de générer de très grands champs magnétiques. Le solénoïde est capable de ces champs élevés provenant de courants élevés circulant à travers des fils supraconducteurs. Le grand champ magnétique est utilisé pour modifier le spin des protons dans le corps du patient. Le temps nécessaire pour que les spins s'alignent ou se relâchent (retour à leur orientation initiale) est une caractéristique des différents tissus qui peut être analysée pour voir si la structure des tissus est normale (Figure\(\PageIndex{3}\)).
Un solénoïde comporte 300 spires enroulées autour d'un cylindre de 1,20 cm de diamètre et de 14,0 cm de long. Si le courant traversant les bobines est de 0,410 A, quelle est l'amplitude du champ magnétique à l'intérieur et à proximité du milieu du solénoïde ?
Stratégie
On nous donne le nombre de tours et la longueur du solénoïde afin de pouvoir trouver le nombre de tours par unité de longueur. Par conséquent, le champ magnétique à l'intérieur et à proximité du milieu du solénoïde est donné par l'équation \ ref {12.30}. À l'extérieur du solénoïde, le champ magnétique est nul.
Solution
Le nombre de tours par unité de longueur est
\[n = \frac{300 \, turns}{0.140 \, m} = 2.14 \times 10^3 \, turns/m.\]
Le champ magnétique produit à l'intérieur du solénoïde est
\[B = \mu_0 nI = (4\pi \times 10^{-7} T \cdot m/A)(2.14 \times 10^3 turns/m)(0.410 \, A)\]
\[B = 1.10 \times 10^{-3}T.\]
L'importance
Cette solution n'est valable que si la longueur du solénoïde est raisonnablement grande par rapport à son diamètre. Cet exemple est un cas où cela est valide.
Quel est le rapport entre le champ magnétique produit à l'aide d'une formule finie et l'approximation infinie pour un angle\(\theta\) de (a)\(85^o\) ? (b)\(89^o\) ? Le solénoïde a 1000 tours sur 50 cm et un courant de 1,0 A circule à travers les bobines
- Solution
-
a. 1,00382 ; b. 1.00015
Toroïdes
Un tore est une bobine en forme de beignet étroitement enroulée avec un fil continu, comme illustré dans la partie (a) de la Figure\(\PageIndex{4}\). Si le tore a N enroulements et que le courant dans le fil est I, quel est le champ magnétique à la fois à l'intérieur et à l'extérieur du tore ?
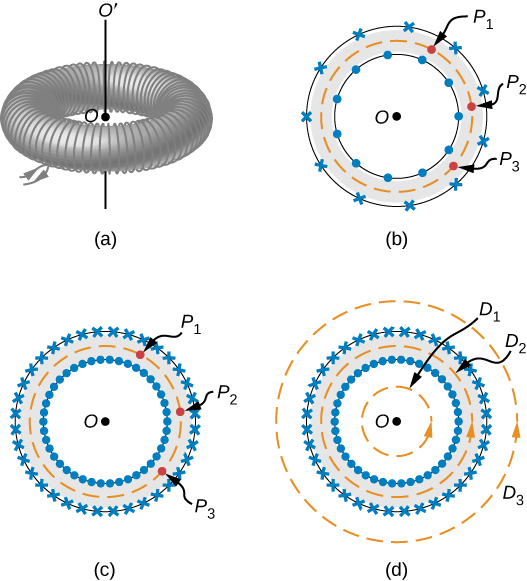
On part de l'hypothèse d'une symétrie cylindrique autour de l'axe OO'. En fait, cette hypothèse n'est pas exactement correcte, car comme le\(\PageIndex{4}\) montre la partie (b) de la figure, la vue de la bobine toroïdale varie d'un point à l'autre (par exemple,\(P_1, \, P_2\) et\(P_3\)) sur une trajectoire circulaire centrée autour de OO '. Cependant, si le tore est étroitement enroulé, tous les points du cercle deviennent essentiellement équivalents [partie (c) de la figure\(\PageIndex{4}\)], et la symétrie cylindrique est une approximation précise.
Avec cette symétrie, le champ magnétique doit être tangent et d'amplitude constante le long de toute trajectoire circulaire centrée sur OO '. Cela nous permet d'écrire pour chacun des chemins\(D_1, \, D_2\) et\(D_3\) comme indiqué dans la partie (d) de la figure\(\PageIndex{4}\),
\[\oint \vec{B} \cdot d\vec{l} = B(2\pi r). \label{12.31}\]
La loi d'Ampère relie cette intégrale au courant net traversant toute surface délimitée par le chemin d'intégration. Pour un trajet externe au tore, soit aucun courant ne traverse la surface enveloppante (chemin\(D_1\)), soit le courant traversant la surface dans une direction est exactement équilibré par le courant qui la traverse dans la direction opposée (trajet\(D_3\)). Dans les deux cas, aucun courant net ne traverse la surface, donc
\[\oint B(2\pi r) = 0\]et
\[B = 0 \, (outside \, the \, toroid). \label{12.32}\]
Les spires d'un tore forment une hélice plutôt que des boucles circulaires. Il en résulte un petit champ extérieur à la bobine ; cependant, la dérivation ci-dessus est valable si les bobines étaient circulaires.
Pour un trajet circulaire à l'intérieur du tore (trajet\(D_2\)), le courant dans le fil coupe la surface N fois, ce qui donne un courant net NI à travers la surface. Nous trouvons maintenant avec la loi d'Ampère,
\[B(2\pi r) = \mu_0 NI\]et
\[B = \frac{\mu_0 NI}{2\pi r} \, (within \, the \, toroid). \label{12.33}\]
Le champ magnétique est dirigé dans le sens antihoraire pour les enroulements représentés. Lorsque le courant dans les bobines est inversé, la direction du champ magnétique s'inverse également.
Le champ magnétique à l'intérieur d'un tore n'est pas uniforme, car il varie inversement avec la distance r de l'axe OO'. Cependant, si le rayon central R (le rayon à mi-chemin entre les rayons intérieur et extérieur du tore) est beaucoup plus grand que le diamètre de la section transversale des bobines r, la variation est assez faible et l'amplitude du champ magnétique peut être calculée par l'équation \ ref {12.33} où \(r = R\).


