12.5 : Champ magnétique d'une boucle de courant
- Page ID
- 191048
À la fin de cette section, vous serez en mesure de :
- Expliquez comment la loi de Biot-Savart est utilisée pour déterminer le champ magnétique dû à un courant dans une boucle de fil en un point situé le long d'une ligne perpendiculaire au plan de la boucle.
- Déterminez le champ magnétique d'un arc de courant.
La boucle circulaire de la Figure\(\PageIndex{1}\) a un rayon R, transporte un courant I et se trouve dans le plan xz. Quel est le champ magnétique dû au courant en un point arbitraire P le long de l'axe de la boucle ?
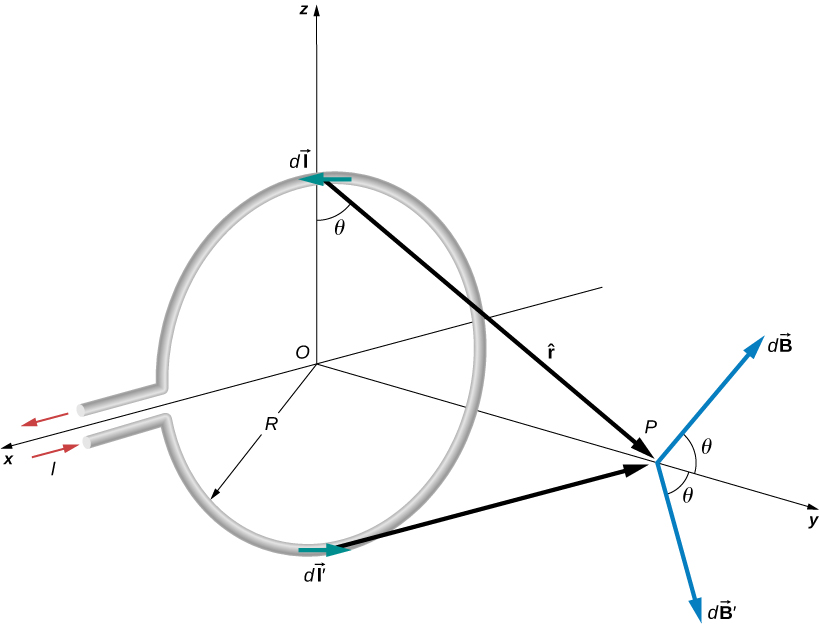
Nous pouvons utiliser la loi de Biot-Savart pour déterminer le champ magnétique dû à un courant. Nous considérons d'abord des segments arbitraires situés sur les côtés opposés de la boucle pour montrer qualitativement par les résultats vectoriels que la direction du champ magnétique net se situe le long de l'axe central à partir de la boucle. À partir de là, nous pouvons utiliser la loi de Biot-Savart pour dériver l'expression du champ magnétique.
Soit P une distance y du centre de la boucle. D'après la règle de droite, le champ magnétique\(d\vec{B}\) en P, produit par l'élément actuel,\(I \, d\vec{l}\) est dirigé selon un angle\(\theta\) au-dessus de l'axe y, comme indiqué. Comme\(d\vec{l}\) il est parallèle le long de l'axe x et\(\hat{r}\) se trouve dans le plan yz, les deux vecteurs sont perpendiculaires, donc nous avons
\[dB = \frac{\mu_0}{4\pi} \frac{I \, dl \, sin \, \pi/2}{r^2} = \frac{\mu_0}{4\pi} \frac{I \, dl}{y^2 + R^2} \label{12.13}\]où nous l'avons utilisé\(r^2 = y^2 + R^2\).
Considérons maintenant le champ magnétique\(d\vec{B}'\) dû à l'élément de courant\(I \, d\vec{l}'\), qui est directement opposé\(I \, d\vec{l}\) sur la boucle. L'amplitude de\(d\vec{B}'\) est également donnée par l'équation \ ref {12.13}, mais elle est dirigée vers un angle θ en dessous de l'axe y. Les composantes de l'axe y\(d\vec{B}\) et\(d\vec{B}'\) perpendiculaires à celui-ci s'annulent donc, et pour calculer le champ magnétique net, seules les composantes situées le long de l'axe y doivent être prises en compte. La somme des composantes perpendiculaires à l'axe de la boucle est nulle par paires. Ainsi, au point P :
\[\vec{B} = \hat{j} \int_{loop} dB \, cos \, \theta = \hat{j} \frac{\mu_0 I}{4\pi} \int_{loop}\frac{cos \, \theta \, dl}{y^2 + R^2}. \label{12.14}\]
Pour tous\(d\vec{l}\) les éléments du fil, y, R et\(\theta\) sont constants et sont liés par
\[cos \, \theta = \frac{R}{\sqrt{y^2 + R^2}}. \nonumber\]
Maintenant, à partir de l'équation \ ref {12.14}, le champ magnétique à P est
\[\vec{B} = \hat{j}\frac{\mu_0IR}{4\pi (y^2 + R^2)^{3/2}} \int_{loop}dl = \frac{\mu_0 IR^2}{2(y^2 + R^2)^{3/2}}\hat{j} \label{12.15}\]où nous l'avons utilisé\(\int_{loop}dl = 2\pi R\). Comme indiqué dans le chapitre précédent, la boucle de courant fermée est un dipôle magnétique du moment\(\vec{\mu} = I \, A\hat{n}\). Pour cet exemple\(\hat{n} = \hat{j}\),\(A = \pi R^2\) et donc le champ magnétique à P peut également être écrit comme
\[\vec{B} = \frac{\mu_0 \mu \hat{j}}{2\pi (y^2 + R^2)^{3/2}}. \label{12.16}\]
\(y = 0\)En définissant l'équation \ ref {12.16}, nous obtenons le champ magnétique au centre de la boucle :
\[\vec{B} = \frac{\mu_0 I}{2R} \hat{j} \label{12.17}.\]
Cette équation devient\(B = \mu_0 n I/(2R)\) pour une bobine plate de n boucles par longueur. Il peut également être exprimé sous la forme
\[\vec{B} = \frac{\mu_0\vec{\mu}}{2\pi R^3}. \label{12.18}\]
Si nous considérons que\(y >> R\) dans l'équation \ ref {12.16}, l'expression se réduit à une expression connue sous le nom de champ magnétique d'un dipôle :
\[\vec{B} = \frac{\mu_0 \vec{\mu}}{2\pi y^3}. \label{12.19}\]
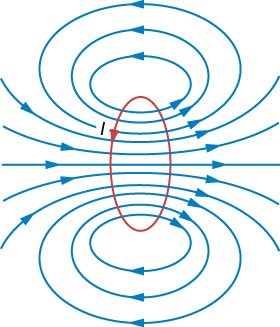
Le calcul du champ magnétique dû à la boucle de courant circulaire à des points hors axe nécessite des mathématiques assez complexes, nous allons donc simplement regarder les résultats. Les lignes de champ magnétique ont la forme indiquée sur la figure\(\PageIndex{2}\). Notez qu'une ligne de champ suit l'axe de la boucle. C'est la ligne de terrain que nous venons de trouver. De plus, très proches du fil, les lignes de champ sont presque circulaires, comme les lignes d'un long fil droit.
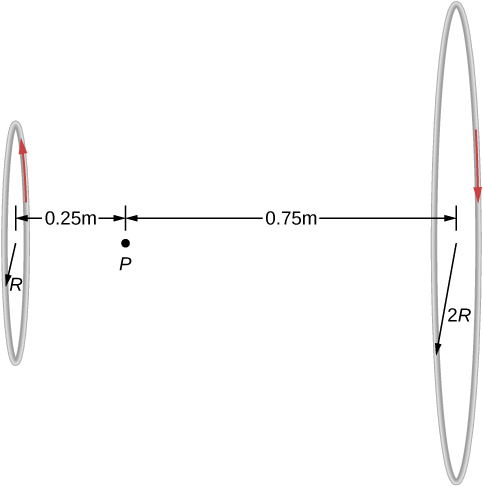
Deux boucles de fil transportent le même courant de 10 mA, mais circulent dans des directions opposées, comme le montre la figure\(\PageIndex{3}\). Une boucle est mesurée pour avoir un rayon de,\(R = 50 \, cm\) tandis que l'autre boucle a un rayon de\(2R = 100 \, cm\). La distance entre la première boucle et le point où le champ magnétique est mesuré est de 0,25 m et la distance entre ce point et la seconde boucle est de 0,75 m. Quelle est l'amplitude du champ magnétique net au point P ?
Stratégie
Le champ magnétique au point P a été déterminé dans l'équation \ ref {12.15}. Comme les courants circulent dans des directions opposées, le champ magnétique net est la différence entre les deux champs générés par les bobines. En utilisant les quantités données dans le problème, le champ magnétique net est ensuite calculé.
Solution
La résolution du champ magnétique net à l'aide de l'équation \ ref {12.15} et des quantités données dans le problème donne
\[B = \frac{\mu_0 IR_1^2}{2(y_1^2 + R_1^2)^{3/2}} - \frac{\mu_0 IR_2^2}{2(y_2^2 + R_2^2)^{3/2}}\]
\[B = \frac{(4\pi \times 10^{-7}T \cdot m/A)(0.010 \, A)(0.5 \, m)^2}{2((0.25 \, m)^2 + (0.5 \, m)^2)^{3/2}} - \frac{(4\pi \times 10^{-7}T \cdot m/A)(0.010 \, A)(1.0 \, m)^2}{2((0.75 \, m)^2 + (1.0 \, m)^2)^{3/2}}\]
\(B = 5.77 \times 10^{-9}T\)vers la droite.
L'importance
Les bobines de Helmholtz ont généralement des boucles de rayons égaux avec un courant circulant dans la même direction afin d'avoir un champ uniforme fort au point médian entre les boucles. Une application similaire de la distribution du champ magnétique créée par les bobines de Helmholtz se trouve dans une bouteille magnétique capable de piéger temporairement des particules chargées. Voir Forces et champs magnétiques pour une discussion à ce sujet.
À l'aide de l'exemple\(\PageIndex{1}\), à quelle distance devriez-vous déplacer la première bobine pour avoir un champ magnétique mesurable nul au point P ?
- Solution
-
0,608 mètres


