7.4 : Calculs du potentiel électrique
- Page ID
- 191237
À la fin de cette section, vous serez en mesure de :
- Calculez le potentiel dû à une recharge ponctuelle
- Calculez le potentiel d'un système de redevances à points multiples
- Décrire un dipôle électrique
- Définir le moment dipolaire
- Calculez le potentiel d'une distribution de charge continue
Les charges ponctuelles, telles que les électrons, font partie des éléments constitutifs fondamentaux de la matière. De plus, les distributions de charge sphériques (telles que la charge sur une sphère métallique) créent des champs électriques externes exactement comme une charge ponctuelle. Le potentiel électrique dû à une charge ponctuelle est donc un cas que nous devons examiner.
Nous pouvons utiliser le calcul pour déterminer le travail nécessaire pour déplacer une charge d'essai q d'une grande distance à une distance de r d'une charge ponctuelle q. En notant le lien entre le travail et le potentiel\(W = -q\Delta V\), comme dans la dernière section, nous pouvons obtenir le résultat suivant.
Le potentiel électrique\(V\) d'une charge ponctuelle est donné par
\[\underbrace{V = \dfrac{kq}{r}}_{\text{point charge}} \label{PointCharge}\]
où\(k\) est une constante égale à\(9.0 \times 10^9 \, N \cdot m^2/C^2\).
Le potentiel dans l'équation \ ref {PointCharge} à l'infini est choisi comme étant nul. Ainsi,\(V\) pour un point, la charge diminue avec la distance, alors que\(\vec{E}\) pour un point, la charge diminue avec la distance au carré :
\[E = \dfrac{F}{q_t} = \dfrac{kq}{r^2}\]
Rappelons que le potentiel électrique V est scalaire et n'a pas de direction, alors que le champ électrique\(\vec{E}\) est un vecteur. Pour déterminer la tension due à une combinaison de charges ponctuelles, vous devez additionner les tensions individuelles sous forme de nombres. Pour déterminer le champ électrique total, vous devez ajouter les champs individuels sous forme de vecteurs, en tenant compte de l'amplitude et de la direction. Ceci est cohérent avec le fait que V est étroitement associé à l'énergie, un scalaire, alors qu'il\(\vec{E}\) est étroitement associé à la force, un vecteur.
Les charges de l'électricité statique se situent généralement\((\mu C)\) entre le nanocoulomb (nC) et le microcoulomb. Quelle est la tension à 5 cm du centre d'une sphère métallique solide de 1 cm de diamètre ayant une charge statique de -3,00 nC ?
Stratégie
Comme nous l'avons vu dans Charges et champs électriques, la charge sur une sphère métallique s'étale uniformément et produit un champ semblable à celui d'une charge ponctuelle située en son centre. Ainsi, nous pouvons trouver la tension à l'aide de l'équation\(V = \dfrac{kq}{r}\).
Solution
En entrant des valeurs connues dans l'expression du potentiel d'une charge ponctuelle (équation \ ref {PointCharge}), nous obtenons
\[\begin{align} V &= k\dfrac{q}{r} \nonumber \\[4pt] &= (9.00 \times 10^9 \, N \cdot m^2/C^2)\left(\dfrac{-3.00 \times 10^{-9}C}{5.00 \times 10^{-2}m}\right) \nonumber \\[4pt] &= - 539 \, V. \nonumber \end{align} \nonumber \]
L'importance
La valeur négative de la tension signifie qu'une charge positive serait attirée à une plus grande distance, car le potentiel est plus faible (plus négatif) que sur de plus grandes distances. À l'inverse, une charge négative serait repoussée, comme prévu.
Un générateur Van de Graaff de démonstration possède une sphère métallique de 25,0 cm de diamètre qui produit une tension de 100 kV à proximité de sa surface (Figure). Quelle charge excédentaire se trouve sur la sphère ? (Supposons que chaque valeur numérique soit représentée ici par trois chiffres significatifs.)
Stratégie
Le potentiel à la surface est le même que celui d'une charge ponctuelle au centre de la sphère, à 12,5 cm de distance. (Le rayon de la sphère est de 12,5 cm.) Nous pouvons ainsi déterminer l'excédent de charge à l'aide de l'équation \ ref {PointCharge}
\[V = \dfrac{kq}{r}.\]
Solution
La résolution\(q\) et la saisie de valeurs connues donnent
\[\begin{align} q &= \dfrac{rV}{k} \nonumber \\[4pt] &= \dfrac{(0.125 \, m)(100 \times 10^3 \, V)}{8.99 \times 10^9 N \cdot m^2/C^2} \nonumber \\[4pt] &= 1.39 \times 10^{-6} C \nonumber \\[4pt] &= 1.39 \, \mu C. \nonumber \end{align} \nonumber \]
L'importance
Il s'agit d'une charge relativement faible, mais elle produit une tension assez importante. Nous avons une autre indication selon laquelle il est difficile de stocker des charges isolées.
Quel est le potentiel à l'intérieur de la sphère métallique dans l'exemple\(\PageIndex{1}\) ?
Solution
\[\begin{align} V &= k\dfrac{q}{r} \nonumber \\[4pt] &= (8.99 \times 10^9 N \cdot m^2/C^2) \left(\dfrac{-3.00 \times 10^{-9} C}{5.00 \times 10^{-3} m}\right) \nonumber \\[4pt] &= - 5390 \, V\nonumber \end{align} \nonumber \]
Rappelez-vous que le champ électrique à l'intérieur d'un conducteur est nul. Ainsi, tout trajet entre un point de la surface et n'importe quel point de l'intérieur aura un integrand de zéro lors du calcul de la variation de potentiel, de sorte que le potentiel à l'intérieur de la sphère est identique à celui de la surface.
Les tensions dans ces deux exemples peuvent être mesurées à l'aide d'un compteur qui compare le potentiel mesuré au potentiel du sol. Le potentiel du sol est souvent considéré comme nul (au lieu de prendre le potentiel à l'infini pour zéro). C'est la différence de potentiel entre deux points qui est importante et, très souvent, on suppose implicitement qu'un point de référence, tel que la Terre ou un point très éloigné, est au potentiel zéro. Comme indiqué précédemment, cela est analogue à la prise du niveau de la mer, comme\(h = 0\) lorsque l'on considère l'énergie potentielle gravitationnelle\(U_g = mgh\).
Systèmes de facturation à points multiples
Tout comme le champ électrique obéit à un principe de superposition, il en va de même pour le potentiel électrique. Prenons l'exemple d'un système composé de N charges\(q_1,q_2,. . ., q_N\). Quel est le potentiel électrique net V à un point spatial P à partir de ces charges ? Chacune de ces charges est une charge source qui produit son propre potentiel électrique au point P, indépendamment de tout autre changement. \(V_1, V_2, . . ., V_N\)Soit les potentiels électriques en P produits par les charges\(q_1,q_2,. . ., q_N\), respectivement. Ensuite, le potentiel électrique net\(V_p\) à ce point est égal à la somme de ces potentiels électriques individuels. Vous pouvez facilement le montrer en calculant l'énergie potentielle d'une charge d'essai lorsque vous amenez la charge d'essai du point de référence à l'infini au point P :
\[V_p = V_1 + V_2 + . . . + V_N = \sum_1^N V_i.\]
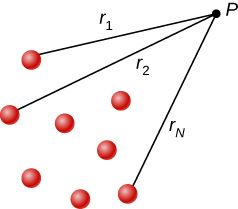
Notez que le potentiel électrique suit le même principe de superposition que le champ électrique et l'énergie potentielle électrique. Pour le montrer plus explicitement, notez qu'une charge d'essai\(q_i\) au point P dans l'espace a des\(r_1,r_2, . . . ,r_N\) distances par rapport aux N charges fixées dans l'espace ci-dessus, comme indiqué sur la figure\(\PageIndex{2}\). En utilisant notre formule pour déterminer le potentiel d'un nombre de points pour chacun de ces frais (supposés être des points), nous constatons que
\[V_p = \sum_1^N k\dfrac{q_i}{r_i} = k\sum_1^N \dfrac{q_i}{r_i}. \label{eq20}\]
Par conséquent, l'énergie potentielle électrique de la charge d'essai est
\[U_p = q_tV_p = q_tk\sum_1^N \dfrac{q_i}{r_i},\]ce qui est identique au travail visant à introduire la charge d'essai dans le système, comme indiqué dans la première section du chapitre.
Le dipôle électrique
Un dipôle électrique est un système de deux charges égales mais opposées à une distance fixe l'une de l'autre. Ce système est utilisé pour modéliser de nombreux systèmes du monde réel, y compris les interactions atomiques et moléculaires. L'un de ces systèmes est la molécule d'eau, dans certaines circonstances. Ces circonstances se rencontrent à l'intérieur d'un four à micro-ondes, où des champs électriques de directions alternées font changer d'orientation les molécules d'eau. Cette vibration est identique à la chaleur au niveau moléculaire.
Considérez le dipôle de la figure\(\PageIndex{3}\) avec l'amplitude de charge\(q = 3.0 \, \mu C\) et la distance de séparation\(d = 4.0 \, cm.\) Quel est le potentiel aux endroits suivants dans l'espace ? (a) (0, 0, 1,0 cm) ; (b) (0, 0, —5,0 cm) ; (c) (3,0 cm, 0, 2,0 cm).
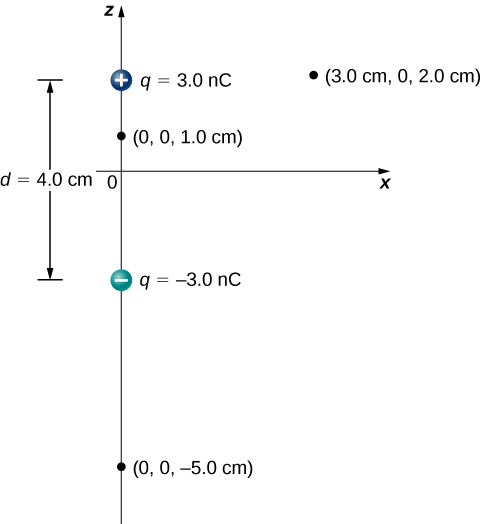
Stratégie
S'applique\(V_p = k \sum_1^N \dfrac{q_i}{r_i}\) à chacun de ces trois points.
Solution
un.\(V_p = k \sum_1^N \dfrac{q_i}{r_i} = (9.0 \times 10^9 \, N \cdot m^2/C^2) \left(\dfrac{3.0\space nC}{0.010 \, m} - \dfrac{3.0\space nC}{0.030 \, m}\right) = 1.8 \times 10^3 \, V\)
b.\(V_p = k \sum_1^N \dfrac{q_i}{r_i} = (9.0 \times 10^9 \, N \cdot m^2/C^2) \left(\dfrac{3.0\space nC}{0.070 \, m} - \dfrac{3.0\space nC}{0.030 \, m}\right) = -5.1 \times 10^2 \, V\)
c.\(V_p = k \sum_1^N \dfrac{q_i}{r_i} = (9.0 \times 10^9 \, N \cdot m^2/C^2) \left(\dfrac{3.0\space nC}{0.030 \, m} - \dfrac{3.0\space nC}{0.050 \, m}\right) = 3.6 \times 10^2 \, V\)
L'importance
Notez que l'évaluation du potentiel est nettement plus simple que celle du champ électrique, car le potentiel est un scalaire et non un vecteur.
Quel est le potentiel sur l'axe X ? L'axe Z
Solution
Sur l'axe x, le potentiel est nul, en raison des charges égales et opposées situées à la même distance de celui-ci. Sur l'axe z, nous pouvons superposer les deux potentiels ; nous constaterons que pour\(z > > d\), encore une fois, le potentiel passe à zéro en raison de l'annulation.
Examinons maintenant le cas particulier où la distance entre le point P et le dipôle est bien supérieure à la distance entre les charges du dipôle,\(r >> d\) par exemple, lorsque nous nous intéressons au potentiel électrique dû à une molécule polarisée telle qu'une molécule d'eau. Ce n'est pas si loin (infini) que nous pouvons simplement traiter le potentiel comme nul, mais la distance est suffisamment grande pour que nous puissions simplifier nos calculs par rapport à l'exemple précédent.
Nous commençons par noter que dans\(\PageIndex{4}\) la figure, le potentiel est donné par
\[V_p = V_+ + V_- = k \left( \dfrac{q}{r_+} - \dfrac{q}{r_-} \right)\]
où
\[r_{\pm} = \sqrt{x^2 + \left(z \pm \dfrac{d}{2}\right)^2}.\]
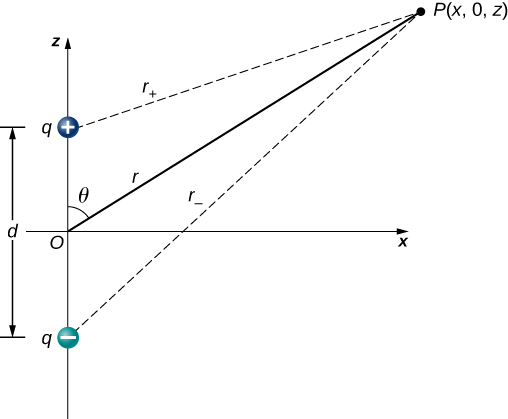
C'est toujours la formule exacte. Pour tirer parti de cela\(r \gg d\), nous réécrivons les rayons en termes de coordonnées polaires, avec\(x = r \, \sin \, \theta\) et z = r \, \ cos \, \ thêta \). Cela nous donne
\[r_{\pm} = \sqrt{r^2 \, \sin^2 \, \theta + \left(r \, \cos \, \theta \pm \dfrac{d}{2} \right)^2}.\]
Nous pouvons simplifier cette expression en retirant r de la racine,
\[r_{\pm} = \sqrt{\sin^2 \, \theta + \left(r \, \cos \, \theta \pm \dfrac{d}{2} \right)^2}\]
puis en multipliant les parenthèses
\[r_{\pm} = r \sqrt{\sin^2\space \theta + \cos^2 \, \theta \pm \cos \, \theta\dfrac{d}{r} + \left(\dfrac{d}{2r}\right)^2} = r\sqrt{1 \pm \cos \, \theta \dfrac{d}{r} + \left(\dfrac{d}{2r}\right)^2}.\]
Le dernier terme de la racine est suffisamment petit pour être négligeable (souvenez-vous que\(r >> d\), et qu'\((d/r)^2\)il est donc extrêmement petit, il est effectivement nul au niveau que nous allons probablement mesurer), ce qui nous laisse
\[r_{\pm} = r\sqrt{1 \pm \cos \, \theta \dfrac{d}{r}}.\]
Utilisation de l'approximation binomiale (résultat standard issu des mathématiques des séries, quand elle\(a\) est petite)
\[\dfrac{1}{\sqrt{1 \pm a}} \approx 1 \pm \dfrac{a}{2}\]
et en le remplaçant dans notre formule\(V_p\), nous obtenons
\[V_p = k\left[\dfrac{q}{r}\left(1 + \dfrac{d \, \cos \, \theta}{2r} \right) - \dfrac{q}{r}\left(1 - \dfrac{d \, \cos \, \theta}{2r}\right)\right] = k\dfrac{qd \, \cos \theta}{r^2}.\]
Cela peut être écrit plus facilement si nous définissons une nouvelle quantité, le moment dipolaire électrique,
\[\vec{p} = q\vec{d},\]
où ces vecteurs pointent de la charge négative à la charge positive. Notez que cela a une magnitude qd. Cette quantité nous permet d'écrire le potentiel au point P dû à un dipôle à l'origine sous la forme
\[V_p = k\dfrac{\vec{p} \cdot \hat{r}}{r^2}.\]
Un schéma de l'application de cette formule est illustré à la figure\(\PageIndex{5}\).
Il existe également des moments d'ordre supérieur, pour les quadrupôles, les octupoles, etc. Vous les verrez dans les prochains cours.
Potentiel des distributions de charge continues
Nous avons beaucoup travaillé avec les charges ponctuelles, mais qu'en est-il des distributions de charge continues ? Rappelez-vous de l'équation \ ref {eq20} que
\[V_p = k\sum \dfrac{q_i}{r_i}.\]
Nous pouvons traiter une distribution de charge continue comme un ensemble de points individuels séparés à l'infini. Cela donne l'intégrale
\[V_p = \int \dfrac{dq}{r}\]
pour le potentiel en un point P. Notez qu'il\(r\) s'agit de la distance entre chaque point individuel de la distribution de charge et le point P. Comme nous l'avons vu dans Charges et champs électriques, les charges infinitésimales sont données par
\[\underbrace{dq = \lambda \, dl}_{one \, dimension}\]
\[\underbrace{dq = \sigma \, dA}_{two \, dimensions}\]
\[\underbrace{dq = \rho \, dV \space}_{three \, dimensions}\]
où\(\lambda\) est la densité de charge linéaire,\(\sigma\) est la charge par unité de surface et\(\rho\) est la charge par unité de volume.
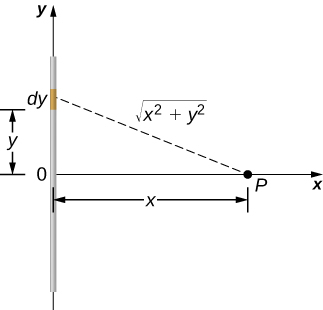
Déterminez le potentiel électrique d'un fil non conducteur chargé uniformément de densité linéaire\(\lambda\) (coulomb/mètre) et de longueur L en un point situé sur une ligne qui divise le fil en deux parties égales.
Stratégie
Pour régler le problème, nous choisissons des coordonnées cartésiennes de manière à exploiter au maximum la symétrie du problème. Nous plaçons l'origine au centre du fil et orientons l'axe y le long du fil de manière à ce que les extrémités du fil soient à\(y = \pm L/2\). Le point de champ P se trouve dans le plan xy et comme le choix des axes dépend de nous, nous choisissons l'axe x pour passer par le point de champ P, comme indiqué sur la figure\(\PageIndex{6}\).
Solution
Considérons un petit élément de la distribution de charge entre y et\(y + dy\). La charge dans cette cellule est\(dq = \lambda \, dy\) et la distance entre la cellule et le point de champ P est\(\sqrt{x^2 + y^2}\). Par conséquent, le potentiel devient
\[\begin{align} V_p &= k \int \dfrac{dq}{r} \nonumber \\[4pt] &= k\int_{-L/2}^{L/2} \dfrac{\lambda \, dy}{\sqrt{x^2 + y^2}} \nonumber \\[4pt] &= k\lambda \left[ln \left(y + \sqrt{y^2 + x^2}\right) \right]_{-L/2}^{L/2} \nonumber \\[4pt] &= k\lambda \left[ ln \left(\left(\dfrac{L}{2}\right) + \sqrt{\left(\dfrac{L}{2}\right)^2 + x^2}\right) - ln\left(\left(-\dfrac{L}{2}\right) + \sqrt{\left(-\dfrac{L}{2}\right)^2 + x^2}\right)\right] \nonumber \\[4pt] &= k\lambda ln \left[ \dfrac{L + \sqrt{L^2 + 4x^2}}{-L + \sqrt{L^2 + 4x^2}}\right]. \nonumber \end{align} \nonumber\]
L'importance
Notez que c'était plus simple que le problème équivalent pour le champ électrique, en raison de l'utilisation de quantités scalaires. Rappelons que nous nous attendons à ce que le niveau zéro du potentiel soit infini, lorsque nous avons une charge finie. Pour examiner cela, nous prenons la limite du potentiel ci-dessus lorsque x approche de l'infini ; dans ce cas, les termes contenus dans le logarithme naturel se rapprochent de un, et donc le potentiel approche zéro dans cette limite. Notez que nous aurions pu résoudre ce problème de manière équivalente en coordonnées cylindriques ; le seul effet serait de substituer r pour x et z pour y.
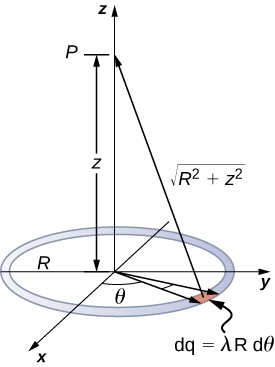
Un anneau a une densité de charge uniforme\(\lambda\), avec des unités de coulomb par unité de mètre d'arc. Déterminez le potentiel électrique à un point de l'axe passant par le centre de l'anneau.
Stratégie
Nous utilisons la même procédure que pour le fil chargé. La différence ici est que la charge est répartie sur un cercle. Nous divisons le cercle en éléments infinitésimaux en forme d'arcs sur le cercle et utilisons les coordonnées cylindriques illustrées sur la figure\(\PageIndex{7}\).
Solution
Un élément général de l'arc entre\(\theta\) et\(\theta + d\theta\) est de longueur\(Rd\theta\) et contient donc une charge égale à\(\lambda Rd\theta\). L'élément se trouve à une distance\(\sqrt{z^2 + R^2}\) de P, et donc le potentiel est
\[\begin{align} V_p &= k\int \dfrac{dq}{r} \nonumber \\[4pt] &= k \int_0^{2\pi} \dfrac{\lambda Rd\theta}{\sqrt{z^2 + R^2}} \nonumber \\[4pt] &= \dfrac{k \lambda R}{\sqrt{z^2 + R^2}} \int_0^{2\pi} d\theta \nonumber \\[4pt] &= \dfrac{2\pi k \lambda R}{\sqrt{z^2 + R^2}} \nonumber \\[4pt] &= k \dfrac{q_{tot}}{\sqrt{z^2 + R^2}}. \nonumber \end{align} \nonumber\]
L'importance
Ce résultat est attendu car chaque élément de l'anneau se trouve à la même distance du point P. Le potentiel net en P est celui de la charge totale placée à la distance commune,\(\sqrt{z^2 + R^2}\).
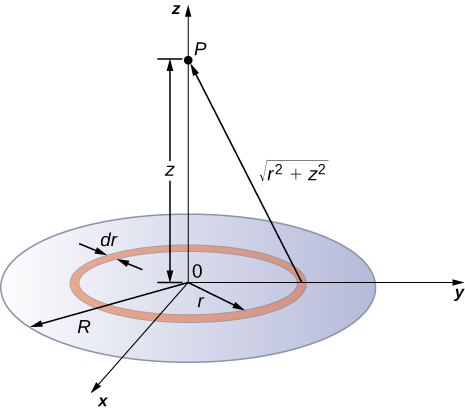
Un disque de rayon R a une densité de charge uniforme\(\sigma\) avec des unités de coulombmètre au carré. Déterminez le potentiel électrique à n'importe quel point de l'axe passant par le centre du disque.
Stratégie
Nous divisons le disque en cellules en forme d'anneau et utilisons le résultat pour un anneau élaboré dans l'exemple précédent, puis nous intégrons sur r en plus de\(\theta\). Ceci est illustré dans la figure\(\PageIndex{8}\).
Solution
Une cellule de largeur infinitésimale comprise entre les coordonnées cylindriques r et\(r + dr\) illustrées sur la figure\(\PageIndex{8}\) sera un anneau de charges dont le potentiel électrique\(dV_p\) au point de champ a l'expression suivante
\[dV_p = k \dfrac{dq}{\sqrt{z^2 + r^2}}\]
où
\[dq = \sigma 2\pi r dr.\]
La superposition du potentiel de tous les anneaux infinitésimaux qui composent le disque donne le potentiel net au point P. Cela se fait en intégrant de\(r = 0\) à\(r = R\) :
\[\begin{align} V_p &= \int dV_p = k2\pi \sigma \int_0^R \dfrac{r \, dr}{\sqrt{z^2 + r^2}}, \nonumber \\[4pt] &= k2\pi \sigma ( \sqrt{z^2 + R^2} - \sqrt{z^2}).\nonumber \end{align} \nonumber\]
L'importance
La procédure de base pour un disque consiste d'abord à intégrer autour de θ, puis sur r. Cela a été démontré pour une densité de charge uniforme (constante). Souvent, la densité de charge varie avec r, puis la dernière intégrale donnera des résultats différents.
Trouvez le potentiel électrique dû à un fil chargé uniformément d'une longueur infinie.
Stratégie
Puisque nous avons déjà déterminé le potentiel d'un fil fini de longueur L dans Example\(\PageIndex{4}\), nous pouvons nous demander si la prise\(L \rightarrow \infty\) en compte de notre résultat précédent fonctionnera :
\[V_p = \lim_{L \rightarrow \infty} k \lambda \ln \left(\dfrac{L + \sqrt{L^2 + 4x^2}}{-L + \sqrt{L^2 + 4x^2}}\right).\]
Cependant, cette limite n'existe pas car l'argument du logarithme devient [2/0] as\(L \rightarrow \infty\), donc cette façon de trouver V d'un fil infini ne fonctionne pas. La raison de ce problème peut être attribuée au fait que les charges ne sont pas localisées dans un certain espace mais continuent à l'infini dans la direction du fil. Par conséquent, notre hypothèse (tacite) selon laquelle le potentiel zéro doit se trouver à une distance infinie du fil n'est plus valide.
Pour éviter cette difficulté de calcul des limites, utilisons la définition du potentiel en intégrant le champ électrique de la section précédente et la valeur du champ électrique issue de cette configuration de charge du chapitre précédent.
Solution
Nous utilisons l'intégrale
\[V_p = - \int_R^p \vec{E} \cdot d\vec{l}\]
où R est une distance finie de la ligne de charge, comme indiqué sur la figure\(\PageIndex{9}\).
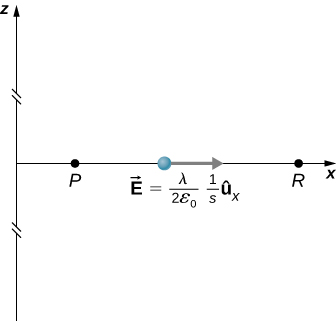
Avec cette configuration, nous utilisons\(\vec{E}_p = 2k \lambda \dfrac{1}{s} \hat{s}\) et\(d\vec{l} = d\vec{s}\) pour obtenir
\[\begin{align} V_p - V_R &= - \int_R^p 2k\lambda \dfrac{1}{s}ds \nonumber \\[4pt] &= -2 k \lambda \ln\dfrac{s_p}{s_R}. \nonumber \end{align} \nonumber\]
Maintenant, si nous définissons le potentiel de référence\(V_R = 0\) à\(s_R = 1 \, m\), cela simplifie
\[V_p = -2 k\lambda \, \ln \, s_p.\]
Notez que cette forme de potentiel est tout à fait utilisable ; elle est de 0 à 1 m et n'est pas définie à l'infini, c'est pourquoi nous n'avons pas pu utiliser cette dernière comme référence.
L'importance
Bien que le calcul direct du potentiel puisse être très pratique, nous venons de trouver un système pour lequel cette stratégie ne fonctionne pas bien. Dans de tels cas, le retour à la définition du potentiel en termes de champ électrique peut offrir une solution.
Quel est le potentiel sur l'axe d'un anneau de charge non uniforme, où se situe la densité de charge\(\lambda (\theta) = \lambda \, \cos \, \theta\) ?
Solution
Il sera nul, car à tous les points de l'axe, il y a des charges égales et opposées à égale distance du point d'intérêt. Notez que cette distribution aura en fait un moment dipolaire.


