6.A : La loi de Gauss (réponses)
- Page ID
- 191110
Vérifiez votre compréhension
6.1. Placez-le de manière à ce que son unité normale soit perpendiculaire à\(\displaystyle \vec{E}\).
6.2. \(\displaystyle mab^2/2\)
6,3 a.\(\displaystyle 3.4×10^5N⋅m^2/C;\)
b.\(\displaystyle −3.4×10^5N⋅m^2/C;\)
c.\(\displaystyle 3.4×10^5N⋅m^2/C;\)
d. 0
6.4. Dans ce cas, il n'y a que\(\displaystyle \vec{E}_{out}\). Donc, oui.
6,5. \(\displaystyle \vec{E}=\frac{λ_0}{2πε_0}\frac{1}{d}\hat{r}\); Cela concorde avec le calcul de l'exemple 5.5 où nous avons trouvé le champ électrique en l'intégrant sur le fil chargé. Remarquez à quel point le calcul de ce champ électrique est beaucoup plus simple avec la loi de Gauss.
6.6. S'il y a d'autres objets chargés autour, les charges à la surface de la sphère ne seront pas nécessairement sphériquement symétriques ; il y en aura davantage dans certaines directions que dans d'autres directions.
Questions conceptuelles
1. a. Si la surface plane est perpendiculaire au vecteur de champ électrique, le flux maximal serait obtenu. b. Si la surface plane était parallèle au vecteur de champ électrique, le flux minimum serait obtenu.
3. vrai
5. Comme le vecteur du champ électrique est\(\displaystyle \frac{1}{r^2}\) dépendant, les flux sont les mêmes depuis\(\displaystyle A=4πr^2\).
7. a. Non ;
b. zéro
9. Les deux champs varient comme\(\displaystyle \frac{1}{r^2}\). Comme la constante gravitationnelle est beaucoup plus petite que\(\displaystyle \frac{1}{4πε_0}\), le champ gravitationnel est plusieurs ordres de grandeur plus faible que le champ électrique.
11. Non, il est produit par toutes les charges à la fois à l'intérieur et à l'extérieur de la surface gaussienne.
13. Non, car la situation n'est pas symétrique, ce qui rend la loi de Gauss difficile à simplifier.
15. N'importe quelle forme de la surface gaussienne peut être utilisée. La seule restriction est que l'intégrale gaussienne doit être calculable ; par conséquent, une boîte ou un cylindre sont les formes géométriques les plus pratiques pour la surface gaussienne.
17. Oui
19. Comme le champ électrique est nul à l'intérieur d'un conducteur, une charge de\(\displaystyle −2.0μC\) est induite sur la surface intérieure de la cavité. Cela mettra une charge de\(\displaystyle +2.0μC\) sur la surface extérieure, laissant une charge nette de\(\displaystyle −3.0μC\) sur la surface.
Problèmes
21. \(\displaystyle Φ=\vec{E}⋅\vec{A}→EAcosθ=2.2×10^4N⋅m^2/C\)champ électrique dans le sens de la normale de l'unité ; champ\(\displaystyle Φ=\vec{E}⋅\vec{A}→EAcosθ=−2.2×10^4N⋅m^2/C\) électrique opposé à la normale de l'unité
23. \(\displaystyle \frac{3×10^{−5}N⋅m^2/C}{(0.05m)^2}=E⇒σ=2.12×10^{−13}C/m^2\)
25. un\(\displaystyle Φ=0.17N⋅m^2/C\) ;.
b.\(\displaystyle Φ=0\) ;
c.\(\displaystyle Φ=EAcos0°=1.0×10^3N/C(2.0×10^{−4}m)^2cos0°=0.20N⋅m^2/C\)
27. \(\displaystyle Φ=3.8×10^4N⋅m^2/C\)
29. \(\displaystyle \vec{E}(z)=\frac{1}{4πε_0}\frac{2λ}{z}\hat{k},∫\vec{E}⋅\hat{n}dA=\frac{λ}{ε_0}l\)
31. un\(\displaystyle Φ=3.39×10^3N⋅m^2/C\) ;.
b.\(\displaystyle Φ=0\) ;
c.\(\displaystyle Φ=−2.25×10^5N⋅m^2/C\) ;
d.\(\displaystyle Φ=90.4N⋅m^2/C\)
33. \(\displaystyle Φ=1.13×10^6N⋅m^2/C\)
35. Créez un cube avec q au centre, en utilisant le cube du côté a. Il faudrait quatre cubes du côté a pour former un côté du grand cube. Le côté ombré du petit cube représenterait 1/24 de la surface totale du grand cube ; par conséquent, le flux à travers la zone ombrée serait de\(\displaystyle Φ=\frac{1}{24}\frac{q}{ε_0}\).
37. \(\displaystyle q=3.54×10^{−7}C\)
39. zéro, également parce que le flux entrant est égal au flux sortant
41. \(\displaystyle r>R,E=\frac{Q}{4πε_0r^2};r<R,E=\frac{qr}{4πε_0R^3}\)
43. \(\displaystyle EA=\frac{λl}{ε_0}⇒E=4.50×10^7N/C\)
45. a. 0 ;
b. 0 ;
c.\(\displaystyle \vec{E}=6.74×10^6N/C(−\hat{r})\)
47. a. 0 ;
b.\(\displaystyle E=2.70×10^6N/C\)
49. a. Oui, la longueur de la tige est bien supérieure à la distance jusqu'au point en question.
b. Non, la longueur de la tige est du même ordre de grandeur que la distance jusqu'au point en question.
c. Oui, la longueur de la tige est bien supérieure à la distance jusqu'au point en question.
d. Non. La longueur de la tige est du même ordre de grandeur que la distance jusqu'au point en question.
51. un\(\displaystyle \vec{E}=\frac{Rσ_0}{ε_0}\frac{1}{r}\hat{r}⇒σ_0=5.31×10^{−11}C/m^2, λ=3.33×10^{−12}C/m\) ;.
b.\(\displaystyle Φ=\frac{q_{enc}}{ε_0}=\frac{3.33×10^{−12}C/m(0.05m)}{ε+0}=0.019N⋅m^2/C\)
53. \(\displaystyle E2πrl=\frac{ρπr^2l}{ε_0}⇒E=\frac{ρr}{2ε_0}(r≤R); E2πrl=\frac{ρπR^2l}{ε_0}⇒E=\frac{ρR^2}{2ε_0r}(r≥R)\)
55. \(\displaystyle Φ=\frac{q_{enc}}{ε_0}⇒q_{enc}=−1.0×10^{−9}C\)
57. \(\displaystyle q_{enc}=\frac{4}{5}παr^5, E4πr^2=\frac{4παr^5}{5ε_0}⇒E=\frac{αr^3}{5ε_0}(r≤R), q_{enc}=\frac{4}{5}παR^5,E4πr^2=\frac{4παR^5}{5ε_0}⇒E=\frac{αR^5}{5ε_0r^2}(r≥R)\)
59. intégrer par pièces :\(\displaystyle q_{enc}=4πρ_0[−e^{−αr}(\frac{(r)^2}{α}+\frac{2r}{α^2}+\frac{2}{α^3})+\frac{2}{α^3}]⇒E=\frac{ρ_0}{r^2ε_0}[−e^{−αr}(\frac{(r)^2}{α}+\frac{2r}{α^2}+\frac{2}{α^3})+\frac{2}{α^3}]\)
61.
63. a. À l'extérieur : à l'intérieur\(\displaystyle E2πrl=\frac{λl}{ε_0}⇒E=\frac{3.0C/m}{2πε_0r}\)\(\displaystyle E_{in}=0\) ;
b.
65. a.\(\displaystyle E2πrl=\frac{λl}{ε_0}⇒E=\frac{λ}{2πε_0r}r≥R\) E à l'intérieur est égal à 0 ;
b.
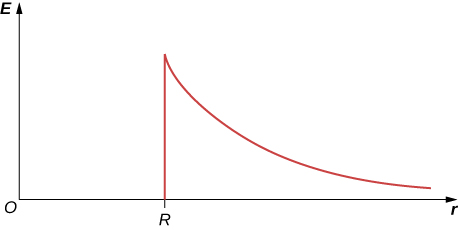
67. \(\displaystyle E=5.65×10^4N/C\)
69. \(\displaystyle λ=\frac{λl}{ε_0}⇒E=\frac{aσ}{ε_0r}r≥a, E=0\)à l'intérieur puisque\(\displaystyle q\) fermé = 0
71. un\(\displaystyle E=0\) ;.
b.\(\displaystyle E2πrL=\frac{Q}{ε_0}⇒E=\frac{Q}{2πε_0rL}\) ; c.\(\displaystyle E=0\) puisque r serait soit à l'intérieur de la deuxième coque, soit à l'extérieur, q entouré vaut 0.
Problèmes supplémentaires
73. \(\displaystyle ∫\vec{E}⋅\hat{n}dA=a^4\)
75. a.\(\displaystyle ∫\vec{E}⋅\hat{n}dA=E_0r^2π\) ; b. zéro, puisque le flux à travers la moitié supérieure annule le flux à travers la moitié inférieure de la sphère
77. \(\displaystyle Φ=\frac{q_{enc}}{ε_0}\); Il y a deux contributions à l'intégrale de surface : l'une sur le côté du rectangle\(\displaystyle x=0\) et l'autre sur le côté à\(\displaystyle x=2.0m\) ;\(\displaystyle −E(0)[1.5m^2]+E(2.0m)[1.5m^2]=\frac{q_{enc}}{ε_0}=−100Nm2^/C\)
où le signe moins indique que at\(\displaystyle x=0\), le champ électrique se trouve le long d'un x positif et que la normale de l'unité est le long d'un x négatif. At\(\displaystyle x=2\), la normale unitaire et le vecteur du champ électrique sont dans la même direction :\(\displaystyle q_{enc}=ε_0Φ=−8.85×10^{−10}C\)
79. n'a pas gardé des directions cohérentes pour les vecteurs de surface ou les champs électriques
81. a.\(\displaystyle σ=3.0×10^{−3}C/m^2, +3×10^{−3}C/m^2\) sur l'un et\(\displaystyle −3×10^{−3}C/m^2\) sur l'autre ;
b.\(\displaystyle E=3.39×10^8N/CE=3.39×10^8N/C\)
83. Construisez un cylindre de Gauss le long de l'axe z avec une section transversale A.
\(\displaystyle |z|≥\frac{a}{2}q_{enc}=ρAa,Φ=\frac{ρAa}{ε_0}⇒E=\frac{ρa}{2ε_0}\),
\(\displaystyle |z|≤\frac{a}{2}q_{enc}=ρA2z,E(2A)=\frac{ρA2z}{ε_0}⇒E=\frac{ρz}{ε_0}\)
85. un\(\displaystyle r>b_2\)\(\displaystyle E4πr^2=\frac{\frac{4}{3}π[ρ_1(b^3_1−a^3_1)+ρ_2(b^3_2−a^3_2)}{ε_0}⇒E=\frac{ρ_1(b^3_1−a^3_1)+ρ_2(b^3_2−a^3_2)}{3ε_0r^2}\) ;.
b.\(\displaystyle a_2<r<b_2\)\(\displaystyle E4πr^2=\frac{\frac{4}{3}π[ρ_1(b^3_1−a^3_1)+ρ_2(r^3−a^3_2)]}{ε_0}⇒E=\frac{ρ_1(b^3_1−a^3_1)+ρ_2(r^3−a^3_2)}{3ε_0r^2}\) ;
c.\(\displaystyle b_1<r<a_2\)\(\displaystyle E4πr^2=\frac{\frac{4}{3}πρ_1(b^3_1−a^3_1)}{ε_0}⇒E=\frac{ρ_1(b^3_1−a^3_1)}{3ε_0r^2}\) ;
d\(\displaystyle a_1<r<b_1\)\(\displaystyle E4πr^2=\frac{\frac{4}{3}πρ_1(r^3_−a^3_1)}{ε_0}⇒E=\frac{ρ_1(r^3−a^3_1)}{3ε_0r^2}\) ;.
e. 0
87. Champ électrique dû à la plaque sans trou :\(\displaystyle E=\frac{σ}{2ε_0}\)
Champ électrique d'un seul trou rempli de \ (\ displaystyle −σE= \ frac {−σ} {2ε_0} (1− \ frac {z} {\ sqrt {R^2+z^2}}).
Ainsi,\(\displaystyle E_{net}=\frac{σ}{2ε_0}\frac{h}{\sqrt{R^2+h^2}}\)
89. a.\(\displaystyle E=0\) ; b.\(\displaystyle E=\frac{q_1}{4πε_0r^2}\) ; c.\(\displaystyle E=\frac{q_1+q_2}{4πε_0r^2}\) ; d. 0\(\displaystyle q_1−q_1, q_1+q_2\)
Problèmes liés au défi
91. Compte tenu du lien référencé, en utilisant une distance de\(\displaystyle 237×10^{15} m\) 4 par rapport à Vega et un diamètre de 2,4 m pour le miroir principal 5, nous constatons qu'à une longueur d'onde de 555,6 nm, Vega émet\(\displaystyle 2.44×10^{24}J/s\) à cette longueur d'onde. Notez que le flux à travers le miroir est essentiellement constant.
93. La symétrie du système oblige\(\displaystyle \vec{E}\) à être perpendiculaire à la feuille et constante sur tout plan parallèle à la feuille. Pour calculer le champ électrique, nous choisissons la surface gaussienne cylindrique illustrée. La section transversale et la hauteur du cylindre sont respectivement A et 2x, et le cylindre est positionné de manière à être coupé en deux par la feuille plane. Comme E est perpendiculaire à chaque extrémité et parallèle au côté du cylindre, nous avons EA comme flux à travers chaque extrémité et il n'y a pas de flux à travers le côté. La charge enfermée par le cylindre est\(\displaystyle σA\), selon la loi de Gauss\(\displaystyle 2EA=\frac{σA}{ε_0}\), et le champ électrique d'une feuille de charge infinie est
\(\displaystyle E=\frac{σ}{2ε_0}\), conformément au calcul indiqué dans le texte.
95. Il y a Q/2 de chaque côté de la plaque puisque la charge nette est\(\displaystyle Q: σ=\frac{Q}{2A}\),
\(\displaystyle ∮_S\vec{E}⋅\hat{n}dA=\frac{2σΔA}{ε_0}⇒E_P=\frac{σ}{ε_0}=\frac{Q}{ε_02A}\)


