4.7 : Entropie
- Page ID
- 191133
À la fin de cette section, vous serez en mesure de :
- Décrire la signification de l'entropie
- Calculez le changement d'entropie pour certains processus simples
La deuxième loi de la thermodynamique s'exprime le mieux en termes de modification de la variable thermodynamique connue sous le nom d'entropie, qui est représentée par le symbole S. L'entropie, comme l'énergie interne, est une fonction de l'état. Cela signifie que lorsqu'un système passe d'un état à un autre, le changement d'entropie\(\Delta S\) est indépendant de la trajectoire et dépend uniquement des variables thermodynamiques des deux états.
Nous considérons\(\Delta S\) d'abord un système soumis à un processus réversible à température constante. Dans ce cas, la variation de l'entropie du système est donnée par
\[\Delta S = \dfrac{Q}{T}, \label{eq1}\]
où\(Q\) est maintenue la chaleur échangée par le système à une température T (en kelvins). Si le système absorbe de la chaleur, c'\(Q > 0\)est-à-dire avec, l'entropie du système augmente. Par exemple, supposons qu'un gaz soit maintenu à une température constante de 300 K alors qu'il absorbe 10 J de chaleur dans le cadre d'un processus réversible. Ensuite, à partir de l'équation \ ref {eq1}, le changement d'entropie du gaz est
\[\Delta S = \dfrac{10 \, J}{300 \, K} = 0.033 \, J/K.\]
De même, si le gaz perd 5,0 J de chaleur,\(Q = -5.0 \, J\) c'est-à-dire à la température\(T = 200 \, K\), nous avons le changement d'entropie du système donné par
\[\Delta S = \dfrac{-5.0 \, J}{200 \, K} = -0.025 \, J/K.\]
De la chaleur est ajoutée lentement à un morceau de glace de 50 g\(0^oC\) jusqu'à ce qu'il soit complètement fondu dans de l'eau à la même température. Qu'est-ce que le changement d'entropie de la glace ?
Stratégie
Comme le processus est lent, nous pouvons l'assimiler à un processus réversible. La température est constante, et nous pouvons donc utiliser l'équation \ ref {eq1} dans le calcul.
Solution
La glace est fondue par l'ajout de chaleur :\[Q = mL_f = 50 \, g \times 335 \, J/g = 16.8 \, kJ. \nonumber\]
Dans ce processus réversible, la température du mélange glace-eau est fixée à\(0^oC\) ou 273 K. À partir de\(\Delta S = Q/T\), le changement d'entropie de la glace est
\[\Delta S = \dfrac{16.8 \, kJ}{273 \, K} = 61.5 \, J/K \nonumber\]
quand il fond pour devenir de l'eau à\(0^oC\).
L'importance
Lors d'un changement de phase, la température est constante, ce qui nous permet d'utiliser l'équation \ ref {eq1} pour résoudre ce problème. La même équation pourrait également être utilisée si nous passons d'une phase liquide à une phase gazeuse, car la température ne change pas non plus au cours de ce processus.
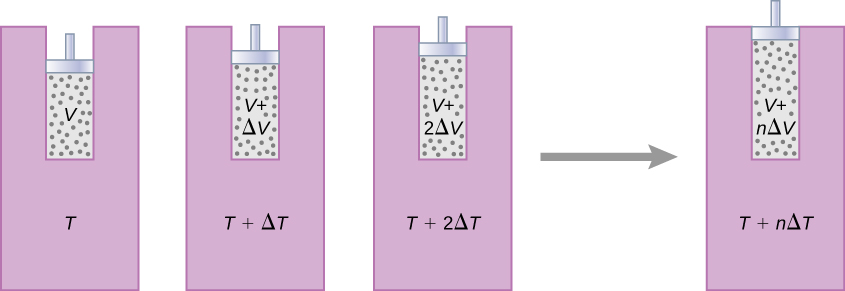
Le changement d'entropie d'un système pour une transition arbitraire et réversible pour laquelle la température n'est pas nécessairement constante est défini par modification\(\Delta S = Q/T\). Imaginez un système passant de l'état A à l'état B en petites étapes discrètes. Les températures associées à ces états sont\(T_A\) et\(T_B\), respectivement. À chaque étape de la transition, le système échange de la chaleur de\(\Delta Q_i\) manière réversible à une température\(T_i\). Cela peut être réalisé expérimentalement en plaçant le système en contact thermique avec un grand nombre de réservoirs de chaleur à des températures variables\(T_i\), comme illustré sur la figure\(\PageIndex{1}\). Le changement d'entropie pour chaque étape est\(\Delta S_i = Q_i/T_i\). La variation nette de l'entropie du système pour la transition est
\[\Delta S = S_B - S_A = \sum_i \Delta S_i = \sum_i \dfrac{\Delta Q_i}{T_i}. \nonumber\]
Nous prenons maintenant la limite au fur\(\Delta Q_i \rightarrow 0\) et à mesure et le nombre de pas approche de l'infini. Ensuite, en remplaçant la sommation par une intégrale, on obtient
\[\Delta S = S_B - S_A = \int_A^B \dfrac{dQ}{T}, \label{eq5} \]
où l'intégrale est prise entre l'état initial A et l'état final B. Cette équation n'est valable que si la transition de A vers B est réversible.
À titre d'exemple, déterminons le changement d'entropie net d'un moteur réversible lorsqu'il subit un seul cycle de Carnot. Dans les étapes adiabatiques 2 et 4 du cycle illustré sur la figure\(\PageIndex{1}\), aucun échange de chaleur n'a lieu, donc\(\Delta S_2 = \Delta S_4 = \int dQ/T = 0\). À l'étape 1, le moteur absorbe de la chaleur\(Q_h\) à une température donnée\(T_h\), donc son changement d'entropie est\(\Delta S_1 = Q_h/T_h\). De même, à l'étape 3,\(\Delta S_3 = -Q_c/T_c\). Le changement d'entropie net du moteur en un cycle de fonctionnement est alors
\[\Delta S_E = \Delta S_1 + \Delta S_2 + \Delta S_3 + \Delta S_4 = \dfrac{Q_h}{T_h} - \dfrac{Q_c}{T_c}.\]
Cependant, nous savons que pour un moteur Carnot,
\[\dfrac{Q_h}{T_h} = \dfrac{Q_c}{T_c},\]
donc
\[\Delta S_E = 0.\]
Il n'y a aucun changement net de l'entropie du moteur Carnot sur un cycle complet. Bien que ce résultat ait été obtenu pour un cas particulier, sa validité peut être démontrée de manière beaucoup plus générale : il n'y a pas de changement net de l'entropie d'un système soumis à un processus cyclique réversible complet. Mathématiquement, nous écrivons cette déclaration comme
\[\oint dS = \oint \dfrac{dQ}{T} = 0 \label{eq10}\]
où\(\oint\) représente l'intégrale sur une trajectoire fermée réversible.
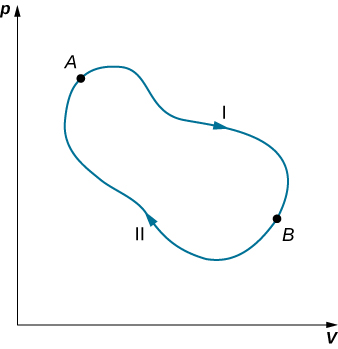
Nous pouvons utiliser l'équation \ ref {eq10} pour montrer que le changement d'entropie d'un système soumis à un processus réversible entre deux états donnés est indépendant du chemin. Un chemin fermé arbitraire pour un cycle réversible passant par les états A et B est illustré sur la figure\(\PageIndex{2}\). À partir de l'équation \ ref {eq10}, nous le savons\(\oint dS = 0\) pour ce chemin fermé. Nous pouvons diviser cette intégrale en deux segments, l'un le long de I, qui mène de A à B, l'autre le long de II, qui mène de B à A. Alors
\[\left[\int_A^BdS\right]_I + \left[\int_B^A dS\right]_{II} = 0\]
Comme le processus est réversible,
\[\left[\int_A^B dS\right] = \left[\int_A^B dS\right] \nonumber\]
Par conséquent, le changement d'entropie lors du passage de A à B est le même pour les voies I et II. Puisque les voies I et II sont des voies arbitraires et réversibles, le changement d'entropie lors d'une transition entre deux états d'équilibre est le même pour tous les processus réversibles joignant ces états. L'entropie, comme l'énergie interne, est donc une fonction d'état.
Que se passe-t-il si le processus est irréversible ? Lorsque le processus est irréversible, on s'attend à ce que l'entropie d'un système fermé, ou du système et de son environnement (l'univers), augmente. Par conséquent, nous pouvons réécrire cette expression comme
\[\Delta S \geq 0,\nonumber \]
où\(S\) est l'entropie totale du système fermé ou de l'univers entier, et le signe égal indique un processus réversible. Le fait est l'énoncé entropique de la deuxième loi de la thermodynamique :
L'entropie d'un système fermé et de l'univers entier ne diminue jamais.
Nous pouvons montrer que cette déclaration est conforme à la déclaration Kelvin, à la déclaration Clausius et au principe Carnot.
Déterminez le changement d'entropie d'un objet de masse m et de chaleur spécifique c qui est refroidi rapidement (et de manière irréversible) à une pression constante de\(T_h\) à\(T_c\).
Stratégie
Le processus est clairement défini comme étant un processus irréversible ; par conséquent, nous ne pouvons pas simplement calculer le changement d'entropie à partir du processus réel. Cependant, comme l'entropie d'un système est fonction de l'état, nous pouvons imaginer un processus réversible qui part du même état initial et se termine à l'état final donné. Ensuite, le changement d'entropie du système est donné par l'équation \ ref {eq5},\(\Delta S = \int_A^B dQ/T\).
Solution
Pour remplacer ce refroidissement rapide par un processus qui se déroule de manière réversible, nous imaginons que l'objet chaud est mis en contact thermique avec des réservoirs de chaleur successivement plus froids dont les températures varient de\(T_h\) à\(T_c\). Tout au long de la transition de substitution, l'objet perd des quantités infinitésimales de chaleur dQ, donc nous avons
\[\Delta S = \int_{T_h}^{T_c} \dfrac{dQ}{T}. \nonumber\]
À partir de la définition de la capacité thermique, un échange infinitésimal dQ pour l'objet est lié à sa variation de température dT par
\[dQ = mcdT. \nonumber\]
En substituant ce dQ à l'expression pour,\(\Delta S\) nous obtenons le changement d'entropie de l'objet lorsqu'il est refroidi à pression constante de\(T_h\) à\(T_c\) :
\[\Delta S = \int_{T_h}^{T_c} \dfrac{mcdT}{T} = mcln\dfrac{T_c}{T_h}. \nonumber\]
Notez cela\(\Delta S < 0\) ici parce que\(T_c > T_h\). En d'autres termes, l'objet a perdu une partie de son entropie. Mais si nous comptons tout ce qui est utilisé pour évacuer la chaleur de l'objet, nous en retrouverons quand même\(S_{universe} > 0\) parce que le processus est irréversible.
L'importance
Si la température change pendant le flux de chaleur, vous devez la maintenir à l'intérieur de l'intégrale pour résoudre le changement d'entropie. Si, toutefois, la température est constante, vous pouvez simplement calculer le changement d'entropie en divisant le flux de chaleur par la température.
Les étapes d'un moteur Stirling réversible sont les suivantes. Pour ce problème, nous utiliserons 0,0010 mol d'un gaz monatomique qui commence à une température\(133^oC\) et un volume de\(0.10 m^3\) ce gaz seront appelés point A. Ensuite, il passe par les étapes suivantes :
- Etape AB : expansion isotherme\(33^oC\) de\(0.20 \, m^3\) à\(0.10 \, m^3\)
- Etape BC : refroidissement isochore pour\(33^oC\)
- Etape CD : compression isotherme\(33^oC\) de\(0.20 \, m^3\) à\(0.10 \, m^3\)
- Étape DA : chauffage isochore vers\(133^oC\) et\(0.10 \, m^3\)
(a) Dessinez le diagramme PV du moteur Stirling avec les étiquettes appropriées.
(b) Remplissez le tableau suivant.
| Étape | W (J) | Q (J) | \(\Delta S\)(J/K) |
|---|---|---|---|
| Étape AB | \ (\ Delta S \) (J/K) « > | ||
| Étape BC | \ (\ Delta S \) (J/K) « > | ||
| Étape CD | \ (\ Delta S \) (J/K) « > | ||
| Étape DA | \ (\ Delta S \) (J/K) « > | ||
| Cycle complet | \ (\ Delta S \) (J/K) « > |
(c) Comment l'efficacité du moteur Stirling se compare-t-elle à celle du moteur Carnot fonctionnant dans les deux mêmes réservoirs de chaleur ?
Stratégie
À l'aide de la loi des gaz idéaux, calculez la pression à chaque point afin qu'ils puissent être étiquetés sur le diagramme pV. Le travail isotherme est calculé à l'aide de\(W = nRT \, ln\left(\frac{V_2}{V_1}\right)\), et aucun travail n'est effectué dans le cadre d'un processus isochore. Le flux de chaleur est calculé à partir de la première loi de la thermodynamique,\(Q = \Delta E_{int} - W\) où\(\Delta E_{int} = \frac{3}{2}nR\Delta T\) pour les gaz monoatomiques. Les étapes isothermes ont une modification de l'entropie de Q/T, alors que les étapes isochores en ont une\(\Delta S = \frac{3}{2}n R \, ln \left(\frac{T_2}{T_1} \right)\). L'efficacité d'un moteur thermique est calculée en utilisant\(e_{Stir} = W/Q_h\).
Solution
- Le graphique est présenté ci-dessous.
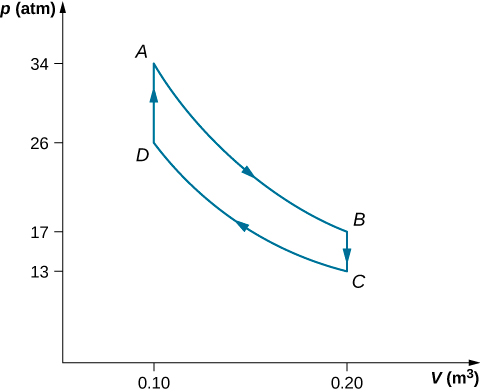
- Le tableau complet est présenté ci-dessous.
Étape W (J) Q (J) \(\Delta S\)(J/K) Étape AB Isotherme 2.3 2.3 \ (\ Delta S \) (J/K) « >0,0057 Étape BC : Isochore 0 —1,2 \ (\ Delta S \) (J/K) « >0,0035 Étape CD Isotherme —1,8 —1,8 \ (\ Delta S \) (J/K) « >—0,0059 Etape DA : Isochore 0 1.2 \ (\ Delta S \) (J/K) « >—0,0035 Cycle complet 0,5 0,5 \ (\ Delta S \) (J/K) « >~ 0 - L'efficacité du moteur thermique Stirling est\[e_{Stir} = W/Q_h = (Q_{AB} + Q_{CD})/(Q_{AB} + Q{DA}) = 0.5/4.5 = 0.11. \nonumber\]
If this were a Carnot engine operating between the same heat reservoirs, its efficiency would be
\[e_{Car} = 1 - \left(\dfrac{T_c}{T_h} \right) = 0.25 \nonumber\]
Therefore, the Carnot engine would have a greater efficiency than the Stirling engine.
Significance
In the early days of steam engines, accidents would occur due to the high pressure of the steam in the boiler. Robert Stirling developed an engine in 1816 that did not use steam and therefore was safer. The Stirling engine was commonly used in the nineteenth century, but developments in steam and internal combustion engines have made it difficult to broaden the use of the Stirling engine.
The Stirling engine uses compressed air as the working substance, which passes back and forth between two chambers with a porous plug, called the regenerator, which is made of material that does not conduct heat as well. In two of the steps, pistons in the two chambers move in phase.


