4.5 : Exposés de la deuxième loi de la thermodynamique
- Page ID
- 191124
À la fin de cette section, vous serez en mesure de :
- Comparez les énoncés de la deuxième loi de la thermodynamique selon les formulations de Kelvin et Clausius
- Interpréter la seconde de la thermodynamique via l'irréversibilité
Plus tôt dans ce chapitre, nous avons présenté l'énoncé de Clausius sur la deuxième loi de la thermodynamique, qui repose sur l'irréversibilité du flux de chaleur spontané. Comme nous l'avons remarqué alors, la deuxième loi de la thermodynamique peut être énoncée de différentes manières, et il peut être démontré que toutes les autres impliquent les autres. En termes de moteurs thermiques, la deuxième loi de la thermodynamique peut être énoncée comme suit :
Il est impossible de convertir la chaleur d'une source unique en travail sans aucun autre effet.
C'est ce que l'on appelle l'énoncé Kelvin de la deuxième loi de la thermodynamique. Cette déclaration décrit un « moteur parfait » inaccessible, tel que représenté schématiquement sur la figure\(\PageIndex{1a}\). Notez que « sans aucun autre effet » est une restriction très stricte. Par exemple, un moteur peut absorber de la chaleur et la transformer en fonctionnement, mais pas s'il complète un cycle. Si un cycle n'est pas terminé, la substance contenue dans le moteur n'est pas dans son état initial et, par conséquent, un « autre effet » s'est produit. Un autre exemple est celui d'une chambre à gaz capable d'absorber la chaleur d'un réservoir de chaleur et de fonctionner de manière isotherme contre un piston lorsqu'il se dilate. Toutefois, si le gaz revenait à son état initial (c'est-à-dire qu'il devait terminer un cycle), il faudrait le comprimer et en extraire de la chaleur.
La déclaration Kelvin est la manifestation d'un problème technique bien connu. Malgré les avancées technologiques, nous ne sommes pas en mesure de construire un moteur thermique\(100\%\) efficace. La première loi n'exclut pas la possibilité de construire un moteur parfait, mais la seconde l'interdit.
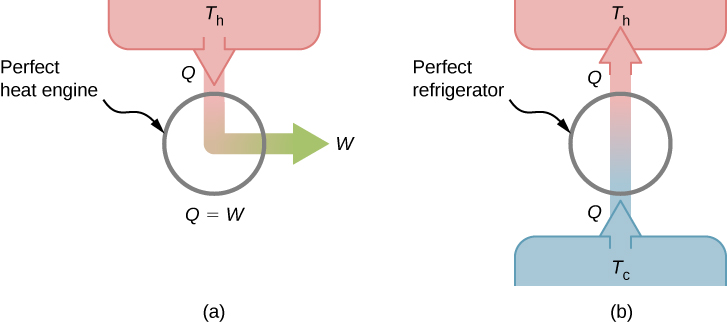
Nous pouvons montrer que l'instruction Kelvin est équivalente à l'instruction Clausius si nous considérons les deux objets de l'instruction Clausius comme un réservoir froid et un réservoir chaud. Ainsi, la déclaration de Clausius devient la suivante : Il est impossible de construire un réfrigérateur qui transfère la chaleur d'un réservoir froid à un réservoir chaud sans l'aide d'une source extérieure. La déclaration de Clausius est liée à l'observation quotidienne selon laquelle la chaleur ne circule jamais spontanément d'un objet froid vers un objet chaud. Le transfert de chaleur dans le sens de l'augmentation de la température nécessite toujours un apport énergétique. Un « réfrigérateur parfait », illustré sur la figure\(\PageIndex{1b}\), qui fonctionne sans une telle aide extérieure, est impossible à construire.
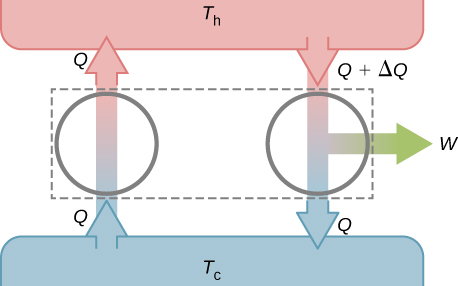
Pour prouver l'équivalence des déclarations de Kelvin et de Clausius, nous démontrons que si une déclaration est fausse, il s'ensuit nécessairement que l'autre déclaration est également fausse. Supposons d'abord que l'affirmation de Clausius soit fausse, de sorte que le réfrigérateur parfait de Figure\(\PageIndex{1b}\) existe. Le réfrigérateur retire la chaleur Q d'un réservoir froid à une certaine température\(T_c\) et la transfère entièrement vers un réservoir chaud à une certaine température\(T_h\). Considérons maintenant un véritable moteur thermique fonctionnant dans la même plage de températures. Il extrait la chaleur\(Q + \Delta Q\) du réservoir chaud, fait fonctionner W et rejette la chaleur Q vers le réservoir froid. À partir de la première loi, ces quantités sont liées par
\[W = (Q + \Delta Q) - Q = \Delta Q.\]
Supposons que ces deux appareils soient combinés comme indiqué sur la figure\(\PageIndex{2}\). La chaleur nette retirée du réservoir chaud est\(\Delta Q\) qu'aucun transfert de chaleur net ne se produit vers ou depuis le réservoir froid, et le travail W est effectué sur un corps externe. Car\(W = \Delta Q\) la combinaison d'un réfrigérateur parfait et d'un véritable moteur thermique est elle-même un moteur thermique parfait, contredisant ainsi l'affirmation de Kelvin. Ainsi, si la déclaration de Clausius est fausse, la déclaration Kelvin doit également l'être.
À l'aide de la deuxième loi de la thermodynamique, nous démontrons maintenant deux propriétés importantes des moteurs thermiques fonctionnant entre deux réservoirs de chaleur. La première propriété est que tout moteur réversible fonctionnant entre deux réservoirs a un rendement supérieur à celui de tout moteur irréversible fonctionnant entre les deux mêmes réservoirs.
La deuxième propriété à démontrer est que tous les moteurs réversibles fonctionnant entre les deux mêmes réservoirs ont le même rendement. Pour le montrer, nous commençons par les deux moteurs D et E de la figure\(\PageIndex{3a}\), qui fonctionnent entre deux réservoirs de chaleur communs à des températures\(T_h\) et\(T_c\). Tout d'abord, nous supposons que D est un moteur réversible et que E est un moteur irréversible hypothétique dont le rendement est supérieur à D. Si les deux moteurs effectuent la même quantité de travail\(W\) par cycle, cela s'ensuit\(Q_h > Q'_h\).\(e=\frac{W}{Q_h}=1-\frac{Q_C}{Q_h}\) Il découle alors de la première loi que\(Q_c > Q'_c\).
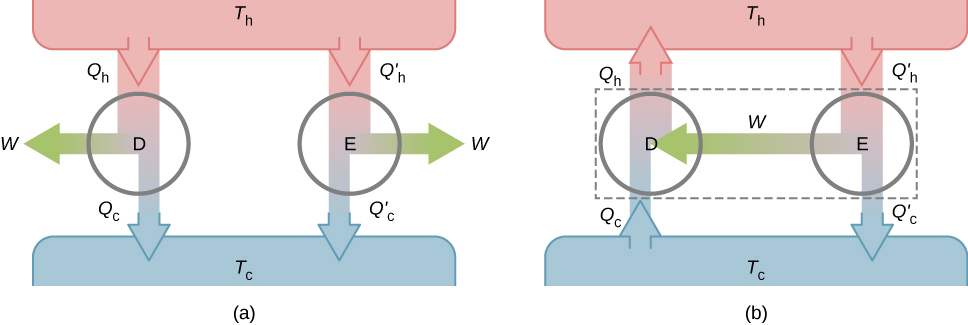
Supposons que le cycle de D soit inversé pour qu'il fonctionne comme un réfrigérateur et que les deux moteurs soient couplés de telle sorte que la puissance de travail de E soit utilisée pour entraîner D, comme indiqué sur la figure\(\PageIndex{3b}\). Puisque\(Q_h > Q'_h\) et\(Q_c > Q'_c\), le résultat net de chaque cycle équivaut à un transfert spontané de chaleur du réservoir froid vers le réservoir chaud, un processus que la deuxième loi ne permet pas. L'hypothèse initiale doit donc être fausse et il est impossible de construire un moteur irréversible de telle sorte que E soit plus efficace que le moteur réversible D.
Il est maintenant assez facile de démontrer que les rendements de tous les moteurs réversibles fonctionnant entre les mêmes réservoirs sont égaux. Supposons que D et E soient tous deux des moteurs réversibles. S'ils sont couplés comme le montre la figure\(\PageIndex{3b}\), l'efficacité de E ne peut pas être supérieure à l'efficacité de D, sinon la deuxième loi serait violée. Si les deux moteurs sont ensuite inversés, le même raisonnement implique que le rendement de D ne peut pas être supérieur à celui de E. La combinaison de ces résultats permet de conclure que tous les moteurs réversibles fonctionnant entre les deux mêmes réservoirs ont le même rendement.
Quelle est l'efficacité d'un moteur thermique parfait ? Quel est le coefficient de performance d'un réfrigérateur parfait ?
Solution
Un moteur thermique parfait aurait\(Q_c = 0\), ce qui conduirait à\(e = 1 - Q_c/Q_h = 1\). Un réfrigérateur parfait ne nécessiterait aucun travail, c'est-à-dire\(W = 0\), ce qui conduit à\(K_R = Q_c/W \rightarrow \infty\).
Montrez cela\(Q_h - Q'_h = Q_c - Q'_c\) pour le moteur hypothétique de la Figure\(\PageIndex{1b}\).
Solution
Depuis le moteur sur la droite, nous avons\(W = Q'_h - Q'_c\). Depuis le réfrigérateur sur la droite, nous avons\(Q_h = Q_c + W\). Ainsi\(W = Q'_h - Q'_c = Q_h - Q_c\).


