Skip to main content
Global

3.6 : Capacités thermiques d'un gaz idéal

  1. Last updated
  2. Save as PDF
  • Page ID
    190992

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objectifs d'apprentissage

    À la fin de cette section, vous serez en mesure de :

    • Définir la capacité thermique d'un gaz idéal pour un procédé spécifique
    • Calculez la chaleur spécifique d'un gaz idéal pour un processus isobare ou isochore
    • Expliquer la différence entre les capacités calorifiques d'un gaz idéal et d'un gaz réel
    • Estimer la variation de la chaleur spécifique d'un gaz sur des plages de températures

    Nous avons déjà découvert la chaleur spécifique et la capacité calorifique molaire ; toutefois, nous n'avons pas envisagé de processus par lequel de la chaleur est ajoutée. C'est ce que nous faisons dans cette section. Nous examinons d'abord un processus dans lequel le système a un volume constant, puis nous le comparons à un système à pression constante et montrons comment leurs chaleurs spécifiques sont liées.

    Commençons par regarder la figure\(\PageIndex{1}\), qui montre deux récipients A et B, contenant chacun 1 mol du même type de gaz idéal à une température T et un volume V. La seule différence entre les deux cuves est que le piston situé au sommet de A est fixe, tandis que celui situé au sommet de B est libre de se déplacer à l'encontre d'une pression extérieure constante p. Nous examinons maintenant ce qui se passe lorsque la température du gaz dans chaque récipient augmente lentement\(T + dT\) avec l'ajout de chaleur.

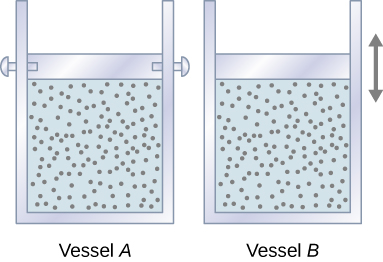
    Deux conteneurs, étiquetés Navire A et Navire B, sont illustrés. Les deux sont remplis de gaz et sont bouchés par un piston. Dans la cuve A, le piston est bloqué. Dans la cuve B, le piston peut coulisser librement, comme indiqué par une double flèche à proximité du piston.
    Figurine\(\PageIndex{1}\): Two vessels are identical except that the piston at the top of A is fixed, whereas that atop B is free to move against a constant external pressure p.

    Since the piston of vessel A is fixed, the volume of the enclosed gas does not change. Consequently, the gas does no work, and we have from the first law

    \[dE_{int} = dQ - dW = dQ.\]

    We represent the fact that the heat is exchanged at constant volume by writing

    \[dQ = C_VndT,\] where \(C_V\) is the molar heat capacity at constant volume of the gas. In addition, since \(dE_{int} = dQ\) for this particular process,

    \[dE_{int} = C_VndT. \label{3.9}\]

    We obtained this equation assuming the volume of the gas was fixed. However, internal energy is a state function that depends on only the temperature of an ideal gas. Therefore, \(dE_{int} = C_VndT\) gives the change in internal energy of an ideal gas for any process involving a temperature change dT.

    When the gas in vessel B is heated, it expands against the movable piston and does work \(dW = pdV\). In this case, the heat is added at constant pressure, and we write \[dQ = C_{p}ndT,\] where \(C_p\) is the molar heat capacity at constant pressure of the gas. Furthermore, since the ideal gas expands against a constant pressure,

    \[d(pV) = d(RnT)\] becomes \[pdV = RndT.\]

    Finally, inserting the expressions for dQ and pdV into the first law, we obtain

    \[dE_{int} = dQ - pdV = (C_{p}n - Rn)dT.\]

    We have found \(dE_{int}\) for both an isochoric and an isobaric process. Because the internal energy of an ideal gas depends only on the temperature, \(dE_{int}\) must be the same for both processes. Thus,

    \[C_{V}ndT = (C_{p}n - Rn)dT,\]

    and

    \[C_p = C_V + R. \label{eq50}\]

    The derivation of Equation \ref{eq50} was based only on the ideal gas law. Consequently, this relationship is approximately valid for all dilute gases, whether monatomic like He, diatomic like \(O_2\), or polyatomic like \(CO_2\) or \(NH_3\).

    In the preceding chapter, we found the molar heat capacity of an ideal gas under constant volume to be

    \[C_V = \dfrac{d}{2}R,\]

    where d is the number of degrees of freedom of a molecule in the system. Table \(\PageIndex{1}\) shows the molar heat capacities of some dilute ideal gases at room temperature. The heat capacities of real gases are somewhat higher than those predicted by the expressions of \(C_V\) and \(C_p\) given in Equation \ref{eq50}. This indicates that vibrational motion in polyatomic molecules is significant, even at room temperature. Nevertheless, the difference in the molar heat capacities, \(C_p - C_V\), is very close to R, even for the polyatomic gases.

    Table \(\PageIndex{1}\): Molar Heat Capacities of Dilute Ideal Gases at Room Temperature
    \(C_p\) \(C_V\) \(C_p - C_V\)
    Type of Molecule Gas \(C_p\)" style="text-align:center;" class="lt-phys-4362">(J/mol K) \(C_V\)" style="text-align:center;" class="lt-phys-4362">(J/mol K) \(C_p - C_V\)" style="text-align:center;" class="lt-phys-4362">(J/mol K)
    Monatomic Ideal \(C_p\)" style="text-align:center;" class="lt-phys-4362">\(\frac{5}{2}R = 20.79\) \(C_V\)" style="text-align:center;" class="lt-phys-4362">\(\frac{3}{2}R = 12.47\) \(C_p - C_V\)" style="text-align:center;" class="lt-phys-4362">\(R = 8.31\)
    Diatomic Ideal \(C_p\)" style="text-align:center;" class="lt-phys-4362">\(\frac{7}{2}R = 29.10\) \(C_V\)" style="text-align:center;" class="lt-phys-4362">\(\frac{5}{2}R = 20.79\) \(C_p - C_V\)" style="text-align:center;" class="lt-phys-4362">\(R = 8.31\)
    Polyatomic Ideal \(C_p\)" style="text-align:center;" class="lt-phys-4362">\(4R = 33.26\) \(C_V\)" style="text-align:center;" class="lt-phys-4362">\(3R = 24.04\) \(C_p - C_V\)" style="text-align:center;" class="lt-phys-4362">\(R = 8.31\)

    Glossary

    molar heat capacity at constant pressure
    quantifies the ratio of the amount of heat added removed to the temperature while measuring at constant pressure
    molar heat capacity at constant volume
    quantifies the ratio of the amount of heat added removed to the temperature while measuring at constant volume