2.4 : Capacité thermique et équirépartition de l'énergie
- Page ID
- 191177
À la fin de cette section, vous serez en mesure de :
- Résoudre les problèmes liés au transfert de chaleur vers et depuis des gaz monoatomiques idéaux dont les volumes sont maintenus constants
- Résoudre des problèmes similaires pour les gaz idéaux non monatomiques en fonction du nombre de degrés de liberté d'une molécule
- Estimer les capacités thermiques des métaux à l'aide d'un modèle basé sur les degrés de liberté
Dans le chapitre sur la température et la chaleur, nous avons défini la capacité thermique spécifique à l'aide de l'équation\(Q = mc\Delta T\), ou\(c = (1/m)Q/\Delta T\). Cependant, les propriétés d'un gaz idéal dépendent directement du nombre de moles dans un échantillon. Nous définissons donc ici la capacité thermique spécifique en termes de nombre de moles, et non de masse. De plus, lorsque nous parlons de solides et de liquides, nous avons ignoré toute variation de volume et de pression liée à des changements de température, une bonne approximation pour les solides et les liquides, mais pour les gaz, nous devons imposer certaines conditions aux variations de volume ou de pression. Ici, nous nous concentrons sur la capacité thermique avec un volume maintenu constant. Nous pouvons le calculer pour un gaz idéal.
Capacité thermique d'un gaz monatomique idéal à volume constant
Nous définissons la capacité thermique molaire à volume constant \(C_V\)comme
\[\underbrace{C_V = \dfrac{1}{n} \dfrac{Q}{\Delta T}}_{\text{with constant V}}\nonumber \]
Ceci est souvent exprimé sous la forme
\[Q = nC_V\Delta T\nonumber \]
Si le volume ne change pas, il n'y a pas de déplacement global, donc aucun travail n'est effectué, et le seul changement d'énergie interne est dû au flux de chaleur\(\Delta E_{int} = Q\). (Cette déclaration est abordée plus en détail dans le chapitre suivant.) Nous utilisons l'équation\(E_{int} = 3nRT/2\) pour écrire\(\Delta E_{int} = 3nR\Delta T/2\) et la remplacer par Q\(\Delta E\) pour trouver\(Q = 3nR\Delta T/2\), ce qui donne le résultat simple suivant pour un gaz monatomique idéal :
\[C_V = \dfrac{3}{2}R.\nonumber \]
Elle est indépendante de la température, ce qui justifie l'utilisation de différences finies au lieu d'une dérivée. Cette formule est en accord avec les résultats expérimentaux.
Dans le chapitre suivant, nous discutons de la chaleur spécifique molaire à pression constante\(C_p\), qui est toujours supérieure à\(C_V\).
Un échantillon de 0,125 kg de xénon est contenu dans un cylindre métallique rigide, suffisamment grand pour que le xénon puisse être modélisé comme un gaz idéal, à une température de\(20.0^oC\). Le cylindre est déplacé à l'extérieur par une chaude journée d'été. Lorsque le xénon s'équilibre en atteignant la température ambiante, 180 J de chaleur lui sont acheminés à travers les parois du cylindre. Qu'est-ce que la température d'équilibre ? Ignorez l'expansion du cylindre métallique.
Solution
- Identifiez les éléments connus : Nous savons que la température initiale\(T_1\) est\(20.0^oC\), que la chaleur Q est de 180 J et que la masse m du xénon est de 0,125 kg.
- Identifiez l'inconnu. Nous avons besoin de la température finale, donc nous en aurons besoin\(\Delta T\).
- Déterminez les équations nécessaires. Comme le xénon est monatomique, on peut l'utiliser\(Q = 3nR\Delta T/2\). Ensuite, nous avons besoin du nombre de taupes\(n = m/M\).
- Remplacez les valeurs connues dans les équations et résolvez les inconnues.
La masse molaire du xénon est de 131,3 g, on obtient donc
\[n = \dfrac{125 \, g}{131.3 \, g/mol} = 0.952 \, mol, \nonumber\nonumber \]
\[\Delta T = \dfrac{2Q}{3nR} = \dfrac{2(180 \, J)}{3(0.952 \, mol)(8.31 \, J/mol \cdot \, ^oC)} = 15.2^oC. \nonumber\nonumber \]
Par conséquent, la température finale est de\(35.2^oC \). Le problème pourrait tout aussi bien être résolu en kelvin ; comme un kelvin est de la même taille qu'un degré Celsius de changement de température, vous obtiendrez\(\Delta T = 15.2 \, K \).
L'importance
Le chauffage d'un gaz idéal ou presque idéal à volume constant est important dans les moteurs automobiles et dans de nombreux autres systèmes pratiques.
Supposons que 2 moles d'hélium à 200 K soient mélangées à 2 moles de krypton à 400 K dans un calorimètre. Quelle est la température finale ?
- Réponse
-
Comme le nombre de moles est égal et que l'on sait que les capacités calorifiques molaires des deux gaz sont égales, la température se situe à mi-chemin entre les températures initiales, 300 K.
Nous aimerions généraliser nos résultats aux gaz idéaux contenant plus d'un atome par molécule. Dans de tels systèmes, les molécules peuvent avoir d'autres formes d'énergie en plus de l'énergie cinétique de translation, telles que l'énergie cinétique de rotation et les énergies cinétiques et potentielles vibrationnelles. Nous verrons qu'une règle simple nous permet de déterminer les énergies moyennes présentes sous ces formes et de résoudre les problèmes de la même manière que nous l'avons fait pour les gaz monoatomiques.
Degrés de liberté
Dans la section précédente, nous avons constaté cela\(\frac{1}{2}mv^2 = \frac{3}{2}k_BT\) et\(v^2 = 3v_x^2\), d'où cela s'ensuit\(\frac{1}{2}mv_x^2 = \frac{1}{2}k_BT\). La même équation vaut pour\(\frac{3}{2}k_BT\) la somme des contributions\(\frac{1}{2}k_BT\) de chacune des trois dimensions du mouvement de translation. En ce qui concerne le gaz dans son ensemble, nous constatons que le 3 de la formule reflète\(C_V = \frac{3}{2}R\) également ces trois dimensions. Nous définissons un degré de liberté comme un mouvement possible indépendant d'une molécule, tel que chacune des trois dimensions de la traduction. Ensuite, si d représente le nombre de degrés de liberté, la capacité thermique molaire à volume constant d'un gaz idéal monatomique est\(C_V = \frac{d}{2}R\), où\(d = 3\).
La branche de la physique appelée mécanique statistique nous indique, et l'expérience le confirme, que\(C_V\) cette équation donne pour tout gaz idéal, quel que soit le nombre de degrés de liberté. Ce fait découle d'un résultat plus général, le théorème d'équipartition, qui s'applique en thermodynamique classique (non quantique) aux systèmes en équilibre thermique dans des conditions techniques qui dépassent notre portée. Ici, nous mentionnons uniquement que dans un système, l'énergie est partagée entre les degrés de liberté par les collisions.
L'énergie d'un système thermodynamique en équilibre est répartie également entre ses degrés de liberté. Par conséquent, la capacité calorifique molaire d'un gaz idéal est proportionnelle à son nombre de degrés de liberté, d :\[C_V = \dfrac{d}{2}R.\nonumber \]
Ce résultat est dû au physicien écossais James Clerk Maxwell (1831−1871), dont le nom apparaîtra plusieurs fois dans ce livre.
Prenons l'exemple d'un gaz diatomique idéal (un bon modèle pour l'\(N_2\)azote et l'oxygène\(O_2\)). Un tel gaz possède plus de degrés de liberté qu'un gaz monatomique. Outre les trois degrés de liberté de translation, il dispose de deux degrés de liberté de rotation perpendiculaires à son axe. De plus, la molécule peut vibrer le long de son axe. Ce mouvement est souvent modélisé en imaginant un ressort reliant les deux atomes, et nous savons par un simple mouvement harmonique que ce mouvement possède à la fois une énergie cinétique et une énergie potentielle. Chacune de ces formes d'énergie correspond à un degré de liberté, ce qui en donne deux autres.
On pourrait s'attendre à ce que, pour un gaz diatomique, nous utilisions 7 comme nombre de degrés de liberté ; classiquement, si les molécules d'un gaz n'avaient qu'une énergie cinétique de translation, les collisions entre molécules les feraient rapidement tourner et vibrer. Cependant, comme expliqué dans le module précédent, la mécanique quantique contrôle les degrés de liberté actifs. Le résultat est illustré dans la figure\(\PageIndex{1}\). Les énergies de rotation et de vibration sont limitées à des valeurs discrètes. Pour des températures inférieures à environ 60 K, les énergies des molécules d'hydrogène sont trop faibles pour qu'une collision fasse passer l'état de rotation ou l'état vibrationnel d'une molécule de la plus faible énergie à la deuxième plus faible. La seule forme d'énergie est donc l'énergie cinétique translationnelle,\(d = 3\) et/ou\(C_V = 3R/2\) comme dans un gaz monatomique. Au-delà de cette température, les deux degrés de liberté de rotation commencent à contribuer, c'est-à-dire que certaines molécules sont excitées vers l'état de rotation avec la deuxième énergie la plus faible. (Cette température est bien inférieure à celle à laquelle contribuent les rotations des gaz monatomiques, car les molécules diatomiques ont des inerties rotationnelles beaucoup plus élevées et donc des énergies de rotation beaucoup plus faibles.) D'environ la température ambiante (un peu moins de 300 K) à environ 600 K, les degrés de liberté de rotation sont pleinement actifs, mais pas les degrés vibratoires, et\(d = 5\). Enfin, au-dessus de 3000 K environ, les degrés de liberté vibratoires sont pleinement actifs, et\(d = 7\) comme le prédit la théorie classique.
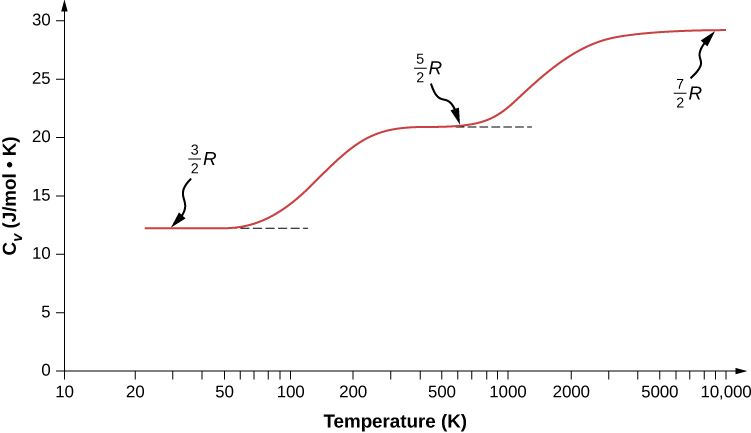
Les molécules polyatomiques ont généralement un degré de liberté de rotation supplémentaire à température ambiante, car elles ont des moments d'inertie comparables autour de n'importe quel axe. Ainsi, à température ambiante, ils ont\(d = 6\) et à haute température,\(d = 8\). Nous supposons généralement que les gaz ont les valeurs théoriques de température ambiante de d.
Comme le montre le tableau\(\PageIndex{1}\), les résultats concordent bien avec les expériences menées sur de nombreux gaz monoatomiques et diatomiques, mais la concordance pour les gaz triatomiques n'est que passable. Les différences proviennent d'interactions que nous avons ignorées entre et au sein des molécules.
| Gaz | \(C_V/R\)à 1\(25^oC\) et 1 atm |
|---|---|
| Ar | \ (C_V/R \) à\(25^oC\) et 1 heure » >1,50 |
| Il | \ (C_V/R \) à\(25^oC\) et 1 heure » >1,50 |
| Nouveau | \ (C_V/R \) à\(25^oC\) et 1 heure » >1,50 |
| CO | \ (C_V/R \) à\(25^oC\) et 1 hame">2,50 |
| \(H_2\) | \ (C_V/R \) à\(25^oC\) et 1 hame">2,47 |
| \(N_2\) | \ (C_V/R \) à\(25^oC\) et 1 hame">2,50 |
| \(O_2\) | \ (C_V/R \) à\(25^oC\) et 1 hame">2,53 |
| \(F_2\) | \ (C_V/R \) à\(25^oC\) et 1 hame">2,8 |
| \(CO_2\) | \ (C_V/R \) à\(25^oC\) et 1 hame">3,48 |
| \(H_2S\) | \ (C_V/R \) à\(25^oC\) et 1 heure du matin » >3,13 |
| \(N_2O\) | \ (C_V/R \) à\(25^oC\) et 1 hame">3,66 |
Qu'en est-il de l'énergie interne des gaz diatomiques et polyatomiques ? Pour de tels gaz, cela\(C_V\) dépend de la température (Figure\(\PageIndex{1}\)), nous n'avons donc pas le type de résultat simple que nous avons pour les gaz idéaux monatomiques.
Capacité thermique molaire des éléments solides
L'idée d'équipartition conduit à une estimation de la capacité calorifique molaire des éléments solides à des températures ordinaires. Nous pouvons modéliser les atomes d'un solide attachés aux atomes voisins par des ressorts (Figure\(\PageIndex{2}\)).
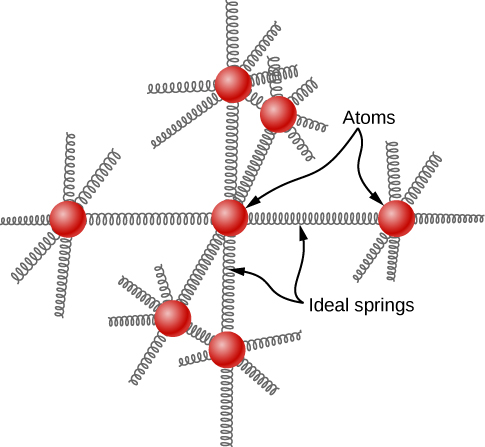
À l'instar de la discussion sur les vibrations dans le module précédent, chaque atome possède six degrés de liberté : un degré cinétique et un potentiel pour chacune des directions x, y et z. En conséquence, la chaleur spécifique molaire d'un métal doit être de 3 R. Ce résultat, connu sous le nom de loi de Dulong et Petit, fonctionne assez bien expérimentalement à température ambiante. (Pour chaque élément, il tombe en panne à basse température pour des raisons de mécanique quantique. Les effets quantiques étant particulièrement importants pour les particules de faible masse, la loi de Dulong et Petit échoue déjà à température ambiante pour certains éléments légers, tels que le béryllium et le carbone. Il échoue également pour certains éléments plus lourds pour diverses raisons au-delà de ce que nous pouvons couvrir.)
La stratégie pour résoudre ces problèmes est la même que celle utilisée dans Phase Changes pour les effets du transfert de chaleur. La seule nouveauté est que vous devez déterminer si le cas qui vient d'être présenté, à savoir des gaz idéaux à volume constant, s'applique au problème. (Pour les éléments solides, il est généralement préférable de rechercher la capacité thermique spécifique que de l'estimer à l'aide de la loi de Dulong et Petit.) Dans le cas d'un gaz idéal, déterminez le nombre d de degrés de liberté à partir du nombre d'atomes dans la molécule de gaz et utilisez-le pour calculer\(C_V\) (ou\(C_V\) utilisez-le pour résoudre d).
Un morceau de 300 g de gallium solide (un métal utilisé dans les dispositifs à semi-conducteurs) à son point de fusion\(30.0^oC\) est uniquement en contact avec 12,0 moles d'air (supposé diatomique)\(95.0^oC\) dans un récipient isolé. Lorsque l'air atteint l'équilibre avec le gallium, 202 g de gallium ont fondu. Sur la base de ces données, quelle est la chaleur de fusion du gallium ? Supposons que le volume d'air ne change pas et qu'il n'y ait aucun autre transfert de chaleur.
Stratégie
Nous allons utiliser l'équation\(Q_{hot} + Q_{cold} = 0\). Comme une partie du gallium ne fond pas, nous savons que la température finale est toujours le point de fusion. Ensuite, la seule\(Q_{hot}\) est la perte de chaleur lorsque l'air se refroidit,\(Q_{hot} = n_{air}C_V\Delta T\), où\(C_V = 5R/2\). La seule\(Q_{cold}\) est la chaleur latente de fusion du gallium,\(Q_{cold} = m_{Ga}L_f\). C'est positif car la chaleur s'écoule dans le gallium.
Solution
- Configurez l'équation :\[n_{air}C_V\Delta T + m_{Ga}L_f = 0.\nonumber \]
- Remplacez les valeurs connues et résolvez :\[(12.0 \, mol) \left(\dfrac{5}{2}\right) \left(8.31 \dfrac{J}{mol \cdot \, ^oC}\right)(30.0^oC - 95.0^oC) + (0.202 \, kg)L_f = 0.\nonumber \]
Nous résolvons de trouver que la chaleur de fusion du gallium est de 80,2 kJ/kg.


