2.5 : Distribution des vitesses moléculaires

Objectifs d'apprentissage

À la fin de cette section, vous serez en mesure de :

• Décrire la distribution des vitesses moléculaires dans un gaz idéal
• Déterminez les vitesses moléculaires moyennes et les plus probables dans un gaz idéal

Les particules d'un gaz idéal se déplacent toutes à des vitesses relativement élevées, mais elles ne se déplacent pas à la même vitesse. La vitesse efficace est une sorte de moyenne, mais de nombreuses particules se déplacent plus vite et beaucoup plus lentement. La distribution réelle des vitesses a plusieurs implications intéressantes pour d'autres domaines de la physique, comme nous le verrons dans les chapitres suivants.

La distribution Maxwell-Boltzmann

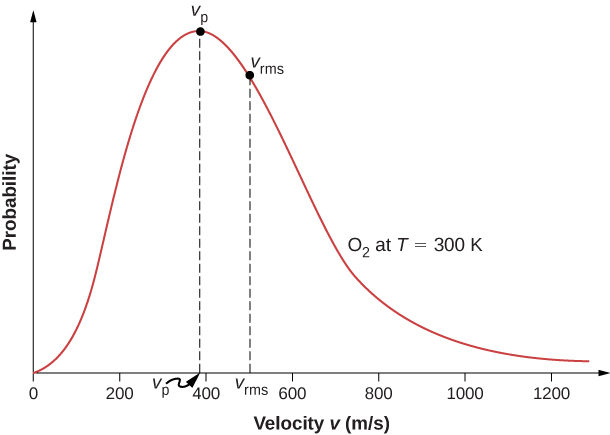
Le mouvement des molécules dans un gaz est aléatoire en amplitude et en direction pour chaque molécule, mais un gaz composé de nombreuses molécules a une distribution prévisible des vitesses moléculaires. Cette distribution prévisible des vitesses moléculaires est connue sous le nom de distribution de Maxwell-Boltzmann, d'après ses auteurs, qui l'ont calculée sur la base de la théorie cinétique, et elle a depuis été confirmée expérimentalement (Figure \(\PageIndex{1}\)).

Pour comprendre cette figure, il faut définir une fonction de distribution des vitesses moléculaires, car avec un nombre fini de molécules, la probabilité qu'une molécule ait exactement une vitesse donnée est de 0.

Figurine\(\PageIndex{1}\): The Maxwell-Boltzmann distribution of molecular speeds in an ideal gas. The most likely speed \(v_p\) is less than the rms speed \(v_{rms}\). Although very high speeds are possible, only a tiny fraction of the molecules have speeds that are an order of magnitude greater than \(v_{rms}\).

We define the distribution function \(f(v)\) by saying that the expected number \(N(v_1, v_2)\) of particles with speeds between \(v_1\) and \(v_2\) is given by

\[N(v_1,v_2) = N\int_{v_1}^{v_2} f(v)dv. \nonumber\]

[Since N is dimensionless, the unit of f(v) is seconds per meter.] We can write this equation conveniently in differential form: \[dN = Nf(v)dv.\]

In this form, we can understand the equation as saying that the number of molecules with speeds between v and \(v + dv\) is the total number of molecules in the sample times f(v) times dv. That is, the probability that a molecule’s speed is between v and \(v + dv\) is f(v)dv.

We can now quote Maxwell’s result, although the proof is beyond our scope.

Maxwell-Boltzmann Distribution of Speeds

The distribution function for speeds of particles in an ideal gas at temperature \(T\) is

\[f(v) = \dfrac{4}{\sqrt{\pi}}\left(\dfrac{m}{2k_BT}\right)^{3/2} v^2e^{-mv^2/2k_BT}.\]

The factors before the \(v^2\) are a normalization constant; they make sure that \(N(0,\infty ) = N\) by making sure that \(\int_0^{|infty} f(v)dv = 1.\) Let’s focus on the dependence on v. The factor of \(v^2\) means that \(f(0) = 0\) and for small v, the curve looks like a parabola. The factor of \(e^{-m_0v^2/2k_BT}\) means that \(\lim_{v\rightarrow \infty} f(v) = 0\) and the graph has an exponential tail, which indicates that a few molecules may move at several times the rms speed. The interaction of these factors gives the function the single-peaked shape shown in the figure.

Example \(\PageIndex{1}\): Calculating the Ratio of Numbers of Molecules Near Given Speeds

In a sample of nitrogen \(N_2\) with a molar mass of 28.0 g/mol) at a temperature of \(273^oC\) find the ratio of the number of molecules with a speed very close to 300 m/s to the number with a speed very close to 100 m/s.

Strategy

Since we’re looking at a small range, we can approximate the number of molecules near 100 m/s as \(dN_{100} = f(100 \, m/s)dv\). Then the ratio we want is

\[\dfrac{dN_{300}}{dN_{100}} = \dfrac{f(300 \, m/s)dv}{f(100 \, m/s)dv} = \dfrac{f(300 \, m/s)}{f(100 \, m/s)}. \nonumber\]

All we have to do is take the ratio of the two f values.

Solution

1. Identify the knowns and convert to SI units if necessary. \[T = 300 \, K, \, k_B = 1.38 \times 10^{-23} J/K\] \[M = 0.0280 \, kg/mol \, so \, m = 4.65 \times 10^{-26} \, kg\]
2. Substitute the values and solve. \[\begin{align*} \dfrac{f(300 \, m/s)}{f(100 \, m/s)} &= \dfrac{\frac{4}{\sqrt{\pi}}\left(\frac{m}{2k_BT}\right)^{3/2} (300 \, m/s)^2 exp[-m(300 \, m/s)^2/2k_BT]}{\frac{4}{\sqrt{\pi}}\left(\frac{m}{2k_BT}\right)^{3/2} (100 \, m/s)^2 exp[-m(100 \, m/s)^2 /2k_BT]} \\[4pt] &= \dfrac{(300 \, m/s)^2 exp [-(4.65 \times 10^{-26} \, kg)(300 \, m/s)^2 /2(1.38 \times 10^{-23} J/K) (300 \, K)]}{(100 \, m/s)^2 exp [-(4.65 \times 10^{-26} \, kg)(100 \, m/s)^2 /2(1.38 \times 10^{-23} J/K) (300 \, K)]} \\[4pt] &= 3^2 exp \left[-\dfrac{(4.65 \times 10^{-26} kg)[(300 \, m/s)^2 - (100 \, m/s)^2]}{2(1.38 \times 10^{-23} \, J/K)(300 \, K)} \right] = 5.74 \end{align*}\]

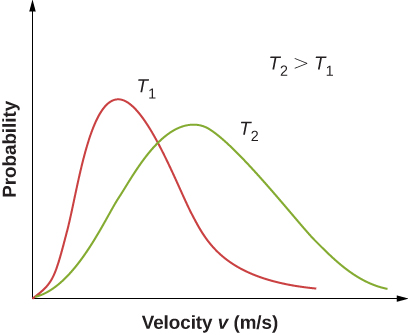
Figure \(\PageIndex{2}\) shows that the curve is shifted to higher speeds at higher temperatures, with a broader range of speeds.

Figure\(\PageIndex{2}\) : La distribution de Maxwell-Boltzmann est déplacée vers des vitesses plus élevées et élargie à des températures plus élevées.

Avec un nombre relativement restreint de molécules, la distribution des vitesses fluctue autour de la distribution de Maxwell-Boltzmann. Cependant, vous pouvez visionner cette simulation pour voir les caractéristiques essentielles selon lesquelles les molécules plus massives se déplacent plus lentement et ont une distribution plus étroite. Utilisez le réglage « 2 gaz, vitesses aléatoires ». Notez l'affichage en bas qui compare les histogrammes des distributions de vitesse avec les courbes théoriques.

Nous pouvons utiliser une distribution de probabilité pour calculer les valeurs moyennes en multipliant la fonction de distribution par la quantité à moyenner et en intégrant le produit sur toutes les vitesses possibles. (Cela est similaire au calcul des moyennes de distributions discrètes, dans lequel vous multipliez chaque valeur par le nombre de fois qu'elle se produit, additionnez les résultats et divisez par le nombre de valeurs. L' intégrale est analogue aux deux premières étapes, et la normalisation est analogue à la division par le nombre de valeurs.) Ainsi, la vitesse moyenne est

\ [\ overline {v} = \ int_0^ {\ infty} vf (v) dv = \ sqrt {\ dfrac {8} {\ pi}  \ dfrac {k_BT} {m}} = \ sqrt {\ dfrac {8} {\ pi} \ dfrac {RT} {M}}. \]

De même,

\ [v_ {rms} = \ sqrt {\ overline {v} ^2} = \ sqrt {\ int_0^ {\ infty} v^2 f (v) dv} = \ sqrt {\ dfrac {3k_BT} {m}} = \ sqrt {\ dfrac {3RT} {M}} \]

comme dans la pression, la température et la vitesse RMS. La vitesse la plus probable, également appelée vitesse de pointe,\(v_p\) est la vitesse au sommet de la distribution des vitesses. (En statistiques, cela s'appellerait le mode.) Elle est inférieure à la vitesse efficace\(v_{rms}\). La vitesse la plus probable peut être calculée par la méthode la plus courante qui consiste à fixer la dérivée de la fonction de distribution, par rapport à v, à 0. Le résultat est

\[v_p = \sqrt{\dfrac{2k_BT}{m}} = \sqrt{\dfrac{2RT}{M}},\]

ce qui est inférieur à\(v_{rms}\). En fait, la vitesse efficace est supérieure à la fois à la vitesse la plus probable et à la vitesse moyenne.

La vitesse maximale fournit un moyen parfois plus pratique d'écrire la fonction de distribution Maxwell-Boltzmann :

\[f(v) = \dfrac{4v^2}{\sqrt{\pi}v_p^3}e^{-v^2/v_p^2}\]

Dans le facteur\(e^{-mv^2/2k_BT}\), il est facile de reconnaître l'énergie cinétique de translation. Ainsi, cette expression est égale à \(e^{-K/k_BT}\). La distribution f (v) peut être transformée en une distribution d'énergie cinétique en l'exigeant \(f(K)dK = f(v)dv\). Boltzmann a montré que la formule résultante est beaucoup plus généralement applicable si l'on remplace l'énergie cinétique de translation par l'énergie mécanique totale E. Le résultat de Boltzmann est

\ [f (E) = \ dfrac {2} {\ sqrt {\ pi}} (k_BT) ^ {-3/2} \ sqrt {E} e^ {-e/k_BT} =  \ dfrac {2} {\ sqrt {\ pi} (k_BT) ^ {3/2}}  \ dfrac {\ sqrt {E}} {e^ {e/k_k_k bT}}. \]

La première partie de cette équation, avec l'exponentielle négative, est la manière habituelle de l'écrire. Nous donnons la deuxième partie uniquement pour faire remarquer que\(e^{E/k_BT}\) le dénominateur est omniprésent en mécanique statistique quantique et classique.

Stratégie de résolution de problèmes : Speed Distribution

• Étape 1. Examinez la situation pour déterminer si elle est liée à la distribution des vitesses moléculaires.
• Étape 2. Dressez une liste des quantités données ou pouvant être déduites du problème tel qu'indiqué (identifiez les quantités connues).
• Étape 3. Identifiez exactement ce qui doit être déterminé dans le problème (identifiez les quantités inconnues). Une liste écrite est utile.
• Étape 4. Convertissez les valeurs connues en unités SI appropriées (K pour la température, Pa pour la pression,\(m^3\) pour le volume, molécules pour N et moles pour n). Dans de nombreux cas, cependant, il sera plus pratique d'utiliser R et la masse molaire que d'utiliser\(k_B\) et la masse moléculaire.
• Étape 5. Déterminez si vous avez besoin de la fonction de distribution pour la vitesse ou de celle pour l'énergie, et si vous utilisez une formule pour l'une des vitesses caractéristiques (moyenne, très probablement ou efficace), si vous recherchez un ratio des valeurs de la fonction de distribution ou si vous vous approchez d'une intégrale.
• Étape 6. Résolvez l'équation appropriée pour la loi du gaz idéal pour la quantité à déterminer (la quantité inconnue). Notez que si vous prenez un ratio des valeurs de la fonction de distribution, les facteurs de normalisation se divisent. Ou si vous approximez une intégrale, utilisez la méthode demandée dans le problème.
• Étape 7. Substituez les quantités connues, ainsi que leurs unités, dans l'équation appropriée et obtenez des solutions numériques complètes avec des unités.

Nous pouvons maintenant acquérir une compréhension qualitative d'un casse-tête concernant la composition de l'atmosphère de la Terre. L'hydrogène est de loin l'élément le plus répandu dans l'univers, et l'hélium est de loin le deuxième élément le plus répandu. De plus, l'hélium est constamment produit sur Terre par désintégration radioactive. Pourquoi ces éléments sont-ils si rares dans notre atmosphère ? La réponse est que les molécules de gaz qui atteignent des vitesses supérieures à la vitesse d'échappement de la Terre, soit environ 11 km/s, peuvent s'échapper de l' atmosphère vers l'espace. En raison de la masse plus faible des molécules d'hydrogène et d' hélium, elles se déplacent à des vitesses plus élevées que les autres molécules de gaz, telles que l'azote et l'oxygène. Seules quelques-unes dépassent la vitesse d'échappement, mais beaucoup moins de molécules plus lourdes le font. Ainsi, au cours des milliards d'années d'existence de la Terre, beaucoup plus de molécules d'hydrogène et d' hélium se sont échappées de l'atmosphère que d'autres molécules, et pratiquement aucune de ces molécules n'est présente aujourd'hui.

Nous pouvons également examiner de nouveau le refroidissement par évaporation, dont nous avons parlé dans le chapitre sur la température et la chaleur. Les liquides, comme les gaz, ont une distribution d'énergies moléculaires. Les molécules les plus énergétiques sont celles qui peuvent échapper aux attraits intermoléculaires du liquide. Ainsi, lorsqu'une partie du liquide s'évapore, les molécules qui restent ont une énergie moyenne plus faible et le liquide a une température plus basse.