6.6 : Les ondes de matière de De Broglie
- Page ID
- 189638
À la fin de cette section, vous serez en mesure de :
- Décrivez l'hypothèse de Broglie concernant les ondes de matière
- Expliquer comment l'hypothèse de de Broglie justifie la quantification du moment cinétique dans la théorie quantique de l'atome d'hydrogène de Bohr
- Décrire l'expérience Davisson-Germer
- Interpréter l'idée de Broglie des ondes de matière et de la façon dont elles expliquent les phénomènes de diffraction des électrons
La formule de Compton a établi qu'une onde électromagnétique peut se comporter comme une particule de lumière lorsqu'elle interagit avec la matière. En 1924, Louis de Broglie a proposé une nouvelle hypothèse spéculative selon laquelle les électrons et autres particules de matière peuvent se comporter comme des ondes. Aujourd'hui, cette idée est connue sous le nom d'hypothèse de Broglie sur les ondes de matière. En 1926, l'hypothèse de De Broglie et les débuts de la théorie quantique de Bohr ont conduit au développement d'une nouvelle théorie de la mécanique quantique des ondes pour décrire la physique des atomes et des particules subatomiques. La mécanique quantique a ouvert la voie à de nouvelles inventions et technologies d'ingénierie, telles que le laser et l'imagerie par résonance magnétique (IRM). Ces nouvelles technologies sont à l'origine de découvertes dans d'autres sciences telles que la biologie et la chimie.
Selon l'hypothèse de Broglie, les photons sans masse ainsi que les particules massives doivent satisfaire à un ensemble commun de relations qui relient l'énergie\(E\) à la fréquence\(f\) et le moment\(p\) linéaire à la longueur d'onde\(λ\). Nous avons discuté de ces relations pour les photons dans le contexte de l'effet Compton. Nous les rappelons maintenant dans un contexte plus général. Toute particule qui possède de l'énergie et de la quantité de mouvement est une onde de Broglie de fréquence\(f\) et de longueur d'onde\(\lambda\) :
\[ E = h f \label{6.53} \]
\[ \lambda = \frac{h}{p} \label{6.54} \]
Voici\(E\) et\(p\) se trouvent respectivement l'énergie relativiste et la quantité de mouvement d'une particule. Les relations de De Broglie sont généralement exprimées en termes de vecteur\(\vec{k}\) d'onde et de fréquence d'onde\(\omega = 2 \pi f\), comme nous le faisons habituellement pour les ondes :\(k = 2 \pi / \lambda\)
\ begin {aligné}
&E= \ hbar \ omega \ label {6,55} \ \
& \ vec {p} = \ hbar \ vec {k} \ label {6,56}
\ end {aligné}
La théorie des ondes nous dit qu'une onde transporte son énergie avec la vitesse du groupe. Pour les ondes de matière, cette vitesse de groupe est la vitesse\(u\) de la particule. En identifiant l'énergie E et le moment p d'une particule avec son énergie relativiste\(mc^2\) et son moment relativiste\(mu\), respectivement, il ressort des relations de Broglie que les ondes de matière répondent à la relation suivante :
\[ \lambda f =\frac{\omega}{k}=\frac{E / \hbar}{p / \hbar}=\frac{E}{p} = \frac{m c^{2}}{m u}=\frac{c^{2}}{u}=\frac{c}{\beta} \label{6.57} \]
où\(\beta = u/c\). Quand une particule est sans masse, nous avons\(u=c\) et l'équation \ ref {6.57} devient\(\lambda f = c\).
Calculez la longueur d'onde de Broglie de :
- un ballon de basket de 0,65 kg lancé à une vitesse de 10 m/s,
- un électron non relativiste avec une énergie cinétique de 1,0 eV, et
- un électron relativiste d'une énergie cinétique de 108 keV.
Stratégie
Nous utilisons l'équation \ ref {6.57} pour trouver la longueur d'onde de Broglie. Lorsque le problème implique un objet non relativiste se déplaçant avec une vitesse u non relativiste, comme dans (a) lorsque\(\beta=u / c \ll 1\), nous utilisons un moment non relativiste p. Lorsque l'approximation non relativiste ne peut pas être utilisée, comme dans (c), nous devons utiliser le moment relativiste\(p=m u=m_{0} \gamma u=E_{0} \gamma \beta/c\), où l'énergie massique restante d'une particule est\(E_0 = m c^2 \) et\(\gamma\) est le facteur de Lorentz\(\gamma=1 / \sqrt{1-\beta^{2}}\). L'énergie totale\(E\) d'une particule est donnée par l'équation \ ref {6.53} et l'énergie cinétique est\(K=E-E_{0}=(\gamma-1) E_{0}\). Lorsque l'énergie cinétique est connue, nous pouvons inverser l'équation 6.4.2 pour trouver la quantité de mouvement
\[ p=\sqrt{\left(E^{2}-E_{0}^{2}\right) / c^{2}}=\sqrt{K\left(K+2 E_{0}\right)} / c \nonumber \]
et remplacez-la dans l'équation \ ref {6.57} pour obtenir
\[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}} \label{6.58} \]
Selon le problème à résoudre, dans cette équation, nous pouvons utiliser les valeurs suivantes pour hc :
\[ h c=\left(6.626 \times 10^{-34} \: \mathrm{J} \cdot \mathrm{s}\right)\left(2.998 \times 10^{8} \: \mathrm{m} / \mathrm{s}\right)=1.986 \times 10^{-25} \: \mathrm{J} \cdot \mathrm{m}=1.241 \: \mathrm{eV} \cdot \mu \mathrm{m} \nonumber \]
Solution
- Pour le basket, l'énergie cinétique est\[ K=m u^{2} / 2=(0.65 \: \mathrm{kg})(10 \: \mathrm{m} / \mathrm{s})^{2} / 2=32.5 \: \mathrm{J} \nonumber \] et le reste de l'énergie massique est.\[ E_{0}=m c^{2}=(0.65 \: \mathrm{kg})\left(2.998 \times 10^{8} \: \mathrm{m} / \mathrm{s}\right)^{2}=5.84 \times 10^{16} \: \mathrm{J} \nonumber \] Nous voyons cela\(K /\left(K+E_{0}\right) \ll 1\) et utilisons\(p=m u=(0.65 \: \mathrm{kg})(10 \: \mathrm{m} / \mathrm{s})=6.5 \: \mathrm{J} \cdot \mathrm{s} / \mathrm{m} \) :\[ \lambda=\frac{h}{p}=\frac{6.626 \times 10^{-34} \: \mathrm{J} \cdot \mathrm{s}}{6.5 \: \mathrm{J} \cdot \mathrm{s} / \mathrm{m}}=1.02 \times 10^{-34} \: \mathrm{m} \nonumber \]
- Pour l'électron non relativiste,\[ E_{0}=mc^{2}=\left(9.109 \times 10^{-31} \mathrm{kg}\right)\left(2.998 \times 10^{8} \mathrm{m} / \mathrm{s}\right)^{2}=511 \mathrm{keV} \nonumber \] et quand\(K = 1.0 \: eV\), nous l'avons fait\(K/(K+E_0) = (1/512) \times 10^{-3} \ll 1\), nous pouvons donc utiliser la formule non relativiste. Cependant, il est plus simple d'utiliser ici l'équation \ ref {6.58} :\[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}}=\frac{1.241 \: \mathrm{eV} \cdot \mu \mathrm{m}}{\sqrt{(1.0 \: \mathrm{eV})[1.0 \: \mathrm{eV}+2(511 \: \mathrm{keV})]}}=1.23 \: \mathrm{nm} \nonumber \] Si nous utilisons le moment non relativiste, nous obtenons le même résultat car 1 eV est beaucoup plus petit que la masse restante de l'électron.
- Pour un électron rapide avec\(K=108 \: keV\), les effets relativistes ne peuvent être négligés car son énergie totale est\(E = K = E_0 = 108 \: keV + 511 \: keV = 619 \: keV\) et n'\(K/E = 108/619\)est pas négligeable :\[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}}=\frac{1.241 \: \mathrm{eV} \cdot \mu \mathrm{m}}{\sqrt{108 \: \mathrm{keV}[108 \: \mathrm{keV}+2(511 \: \mathrm{keV})]}}=3.55 \: \mathrm{pm} \nonumber \].
L'importance
Ces estimations montrent que les longueurs d'onde d'objets macroscopiques tels qu'une balle sont incommensurablement petites selon De Broglie. Par conséquent, même s'ils existent, ils ne sont pas détectables et n'affectent pas le mouvement des objets macroscopiques.
Quelle est la longueur d'onde de Broglie d'un proton non relativiste avec une énergie cinétique de 1,0 eV ?
- Réponse
-
17 h
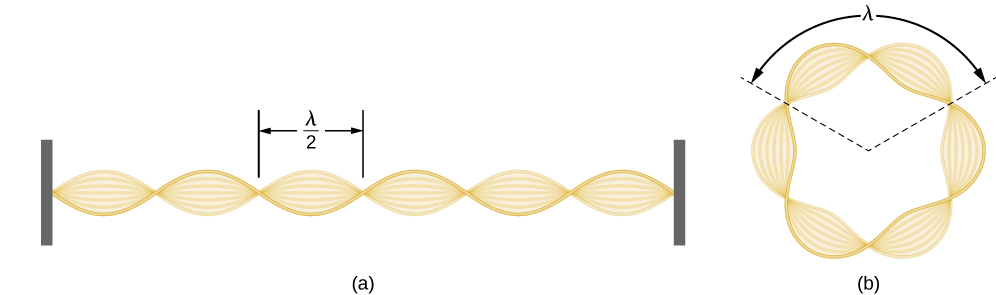
En utilisant le concept de l'onde de matière électronique, de Broglie a justifié la quantification du moment cinétique de l'électron dans l'atome d'hydrogène, qui a été postulée dans la théorie quantique de Bohr. L'explication physique de la première condition de quantification de Bohr vient naturellement lorsque nous supposons qu'un électron d'un atome d'hydrogène se comporte non pas comme une particule mais comme une onde. Pour y voir clair, imaginez une corde de guitare tendue qui est serrée aux deux extrémités et vibre dans l'un de ses modes normaux. Si la longueur de la chaîne est l (Figure\(\PageIndex{1}\)), les longueurs d'onde de ces vibrations ne peuvent pas être arbitraires mais doivent être telles qu'un nombre entier k de demi-longueurs d'onde\(\lambda/2\) corresponde exactement à la distance l entre se termine. C'est la condition\(l=k \lambda /2\) d'une onde stationnaire sur une corde. Supposons maintenant qu'au lieu de serrer la ficelle sur les murs, nous plions sa longueur en cercle et fixons ses extrémités l'une à l'autre. Cela produit une chaîne circulaire qui vibre dans des modes normaux, satisfaisant la même condition d'onde stationnaire, mais le nombre de demi-longueurs d'onde doit maintenant être pair\(k\)\(k=2n\), et la longueur l est maintenant connectée au rayon\(r_n\) du cercle. Cela signifie que les rayons ne sont pas arbitraires mais doivent satisfaire à la condition d'onde stationnaire suivante :
\[ 2 \pi r_{n}=2 n \frac{\lambda}{2} \label{6.59}. \]
Si un électron sur la n ème orbite de Bohr se déplace comme une onde, selon l'équation \ ref {6.59}, sa longueur d'onde doit être égale à\(\lambda = 2 \pi r_n / n\). En supposant que l'équation \ ref {6.58} est valide, l'onde électronique de cette longueur d'onde correspond au moment linéaire de l'électron,\(p = h/\lambda = nh / (2 \pi r_n) = n \hbar /r_n\). Sur une orbite circulaire, le moment cinétique de l'électron doit donc être
\[ L_{n}=r_{n} p=r_{n} \frac{n \hbar}{r_{n}}=n \hbar \label{6.60} . \]
Cette équation est la première des conditions de quantification de Bohr, donnée par l'équation 6.5.6. Fournir une explication physique de la condition de quantification de Bohr est un argument théorique convaincant en faveur de l'existence d'ondes de matière.
Détermine la longueur d'onde de Broglie d'un électron à l'état fondamental de l'hydrogène.
Stratégie
Nous combinons la première condition de quantification de l'équation \ ref {6.60} avec l'équation 6.5.6 et utilisons l'équation 6.5.9 pour le premier rayon de Bohr avec\(n = 1\).
Solution
Quand\(n=1\) et\(r_n = a_0 = 0.529 \: Å\), la condition de quantification de Bohr donne\(a_{0} p=1 \cdot \hbar \Rightarrow p=\hbar / a_{0}\). La longueur d'onde des électrons est :
\[ \lambda=h / p = h / \hbar / a_{0} = 2 \pi a_{0} = 2 \pi(0.529 \: Å)=3.324 \: Å .\nonumber \]
L'importance
Nous obtenons le même résultat lorsque nous utilisons directement l'équation \ ref {6.58}.
Détermine la longueur d'onde de Broglie d'un électron dans le troisième état excité de l'hydrogène.
- Réponse
-
\(\lambda = 2 \pi n a_0 = 2 (3.324 \: Å) = 6.648 \: Å\)
La présence d'ondes de matière a été confirmée expérimentalement en 1927 lorsque C. Davisson et L. Germer ont réalisé une série d'expériences de diffusion d'électrons qui ont clairement montré que les électrons se comportent comme des ondes. Davisson et Germer n'ont pas organisé leur expérience pour confirmer l'hypothèse de Broglie : la confirmation est venue en tant que sous-produit de leurs études expérimentales de routine sur des surfaces métalliques soumises à un bombardement d'électrons.
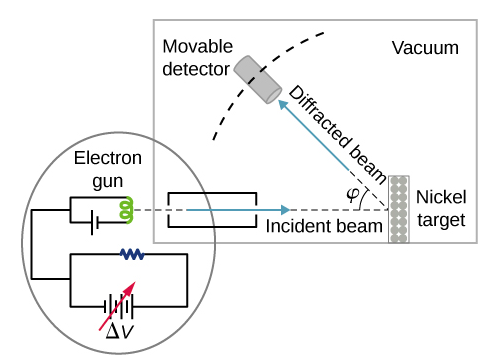
Dans le cadre de l'expérience particulière qui a fourni les toutes premières preuves d'ondes électroniques (connue aujourd'hui sous le nom d'expérience Davisson-Germer), ils ont étudié une surface de nickel. Leur échantillon de nickel a été spécialement préparé dans un four à haute température pour modifier sa structure polycristalline habituelle en une forme dans laquelle de grands domaines monocristallins occupent le volume. La figure\(\PageIndex{2}\) montre la configuration expérimentale. Les électrons thermiques sont libérés par un élément chauffé (généralement constitué de tungstène) dans le canon à électrons et accélérés par une différence de potentiel ΔV, devenant ainsi un faisceau d'électrons bien collimaté produit par un canon à électrons. L'énergie cinétique\(K\) des électrons est ajustée en sélectionnant une valeur de la différence de potentiel dans le canon à électrons. Cela produit un faisceau d'électrons avec une valeur définie de moment linéaire, conformément à la conservation de l'énergie :
\[ e \Delta V=K=\frac{p^{2}}{2 m} \Rightarrow p=\sqrt{2 m e \Delta V} \label{6.61} \]
Le faisceau d'électrons est incident sur l'échantillon de nickel dans la direction normale à sa surface. À la surface, il se disperse dans différentes directions. L'intensité du faisceau diffusé dans une direction sélectionnée φφ est mesurée par un détecteur très sensible. La position angulaire du détecteur par rapport à la direction du faisceau incident peut être modifiée de φ=0° à φ=90°. L'ensemble de l'installation est enfermé dans une chambre à vide pour empêcher les collisions d'électrons avec des molécules d'air, car de telles collisions thermiques modifieraient l'énergie cinétique des électrons et ne sont pas souhaitables.
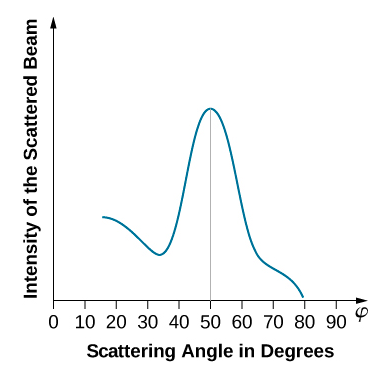
Lorsque la cible en nickel a une forme polycristalline avec de nombreux cristaux microscopiques orientés de manière aléatoire, les électrons incidents se diffusent de sa surface dans diverses directions aléatoires. Par conséquent, l'intensité du faisceau d'électrons diffusé est sensiblement la même dans toutes les directions, ressemblant à une réflexion diffuse de la lumière provenant d'une surface poreuse. Cependant, lorsque la cible de nickel a une structure cristalline régulière, l'intensité du faisceau d'électrons diffusé montre un maximum clair à un angle spécifique et les résultats montrent un diagramme de diffraction clair (voir Figure\(\PageIndex{3}\)). Des diagrammes de diffraction similaires formés par les rayons X diffusés par divers solides cristallins ont été étudiés en 1912 par les physiciens William H. Bragg et William L. Bragg, père et fils. La loi de Bragg en cristallographie aux rayons X fournit un lien entre la longueur\(\lambda\) d'onde du rayonnement incident sur un réseau cristallin, l'espacement entre les réseaux et la position du maximum d'interférence dans le rayonnement diffracté (voir Diffraction).
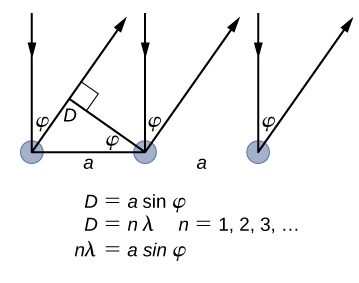
L'espacement entre les réseaux de la cible de Davisson—Germer, déterminé par cristallographie aux rayons X, a été mesuré comme étant\(a=2.15 \: Å\). Contrairement à la cristallographie aux rayons X dans laquelle les rayons X pénètrent dans l'échantillon, dans l'expérience originale de Davisson-Germer, seuls les atomes de surface interagissent avec le faisceau d'électrons incident. Pour la diffraction de surface, l'intensité maximale du faisceau d'électrons réfléchi est observée pour des angles de diffusion qui satisfont à la condition nλ = a sin φ (voir Figure\(\PageIndex{4}\)). Le maximum du premier ordre (pour n = 1) est mesuré à un angle de diffusion de φ≈ 50° à ΔV≈ 54 V, ce qui donne la longueur d'onde du rayonnement incident sous la forme λ= (2,15 Å) sin 50° = 1,64 Å. D'autre part, un potentiel de 54 V accélère les électrons incidents jusqu'à des énergies cinétiques de K = 54 eV. Leur impulsion, calculée à partir de l'équation \ ref {6.61}, est\(p = 2.478 \times 10^{−5} \: eV \cdot s/m\). Lorsque nous substituons ce résultat par l'équation \ ref {6.58}, la longueur d'onde de Broglie est obtenue comme
\[ \lambda=\frac{h}{p}=\frac{4.136 \times 10^{-15} \mathrm{eV} \cdot \mathrm{s}}{2.478 \times 10^{-5} \mathrm{eV} \cdot \mathrm{s} / \mathrm{m}}=1.67 \mathrm{Å} \label{6.62}. \]
Le même résultat est obtenu lorsque nous utilisons K = 54 eV dans l'équation \ ref {6.61}. La proximité de ce résultat théorique avec la valeur expérimentale de Davisson—Germer de λ = 1,64 Å est un argument convaincant en faveur de l'existence d'ondes de matière de de Broglie.
Les raies de diffraction mesurées avec des électrons de faible énergie, telles que celles utilisées dans l'expérience Davisson-Germer, sont assez larges (Figure\(\PageIndex{3}\)) car les électrons incidents sont diffusés uniquement depuis la surface. La résolution des images de diffraction s'améliore considérablement lorsqu'un faisceau d'électrons de plus haute énergie traverse une fine feuille métallique. Cela se produit parce que l'image de diffraction est créée en diffusant de nombreux plans cristallins à l'intérieur du volume, et que les maxima produits lors de la diffusion aux angles de Bragg sont nets (Figure\(\PageIndex{5}\)).

Depuis les travaux de Davisson et Germer, l'hypothèse de de Broglie a été largement testée à l'aide de diverses techniques expérimentales, et l'existence d'ondes de Broglie a été confirmée pour de nombreuses particules élémentaires. Les neutrons ont été utilisés dans des expériences de diffusion pour déterminer les structures cristallines des solides à partir des modèles d'interférence formés par les ondes de matière neutronique. Le neutron a une charge nulle et sa masse est comparable à la masse d'un proton chargé positivement. Les neutrons et les protons peuvent être considérés comme des ondes de matière. Par conséquent, la propriété d'être une onde de matière n'est pas spécifique aux particules chargées électriquement mais vaut pour toutes les particules en mouvement. Des ondes de matière de molécules aussi grosses que le carbone\(C_{60}\) ont été mesurées. Tous les objets physiques, petits ou grands, sont associés à une onde de matière tant qu'ils restent en mouvement. Le caractère universel des ondes de matière de de Broglie est solidement établi.
Supposons qu'un faisceau de neutrons soit utilisé dans une expérience de diffraction sur un solide cristallin typique. Estimez l'énergie cinétique d'un neutron (en eV) dans le faisceau de neutrons et comparez-la à l'énergie cinétique d'un gaz idéal en équilibre à température ambiante.
Stratégie
Nous supposons qu'un espacement cristallin typique a est de l'ordre de 1,0 Å. Pour observer un diagramme de diffraction sur un tel réseau, la longueur d'onde λ des neutrons doit être du même ordre de grandeur que l'espacement entre les réseaux. Nous utilisons l'équation \ ref {6.61} pour trouver le moment p et l'énergie cinétique K. Pour comparer cette énergie à l'énergie\(E_T\) du gaz idéal en équilibre à température ambiante\(T = 300 \, K\), nous utilisons la relation\(K = 3/2 k_BT\), où\(k_B = 8.62 \times 10^{-5}eV/K\) est la constante de Boltzmann.
Solution
Nous évaluons le PC pour le comparer à l'énergie massique restante du neutron\(E_0 = 940 \, MeV\) :
\[p = \frac{h}{\lambda} \Rightarrow pc = \frac{hc}{\lambda} = \frac{1.241 \times 10^{-6}eV \cdot m}{10^{-10}m} = 12.41 \, keV. \nonumber \]
Nous voyons cela\(p^2c^2 << E_0^2\) et nous pouvons utiliser l'énergie cinétique non relativiste :
\[K = \frac{p^2}{2m_n} = \frac{h^2}{2\lambda^2 m_n} = \frac{(6.63\times 10^{−34}J \cdot s)^2}{(2\times 10^{−20}m^2)(1.66 \times 10^{−27} kg)} = 1.32 \times 10^{−20} J = 82.7 \, meV. \nonumber \]
L'énergie cinétique du gaz idéal en équilibre à 300 K est la suivante :
\[K_T = \frac{3}{2}k_BT = \frac{3}{2} (8.62 \times 10^{-5}eV/K)(300 \, K) = 38.8 \, MeV. \nonumber \]
Nous voyons que ces énergies sont du même ordre de grandeur.
L'importance
Les neutrons dont les énergies se situent dans cette gamme, ce qui est typique d'un gaz idéal à température ambiante, sont appelés « neutrons thermiques ».
Dans un supercollisionneur du CERN, les protons peuvent être accélérés à des vitesses de 0,75 c. Quelles sont leurs longueurs d'onde de Broglie à cette vitesse ? Quelles sont leurs énergies cinétiques ?
Stratégie
L'énergie massique restante d'un proton est\(E_0 = m_0c^2 = (1.672 \times 10^{−27} kg)(2.998 \times 10^8m/s)^2 = 938 \, MeV\). Lorsque la vitesse du proton est connue, nous avons β = 0,75 et\(\beta \gamma = 0.75 / \sqrt{1 - 0.75^2} = 1.714\). Nous obtenons la longueur d'onde λλ et l'énergie cinétique K à partir de relations relativistes.
Solution
\[\lambda = \frac{h}{p} = \frac{hc}{\beta \gamma E_0} = \frac{1.241 \, eV \cdot \mu m}{1.714 (938 \, MeV)} = 0.77 \, fm \nonumber \]
\[K = E_0(\gamma - 1) = 938 \, MeV (1 /\sqrt{1 - 0.75^2} - 1) = 480.1\, MeV \nonumber \]
L'importance
Notez qu'étant donné qu'un proton est 1835 fois plus massif qu'un électron, si cette expérience était réalisée avec des électrons, un simple redimensionnement de ces résultats nous donnerait la longueur d'onde de l'électron de (1835) 0,77 fm = 1,4 pm et son énergie cinétique de 480,1 MeV /1835 = 261,6 keV.
Déterminez la longueur d'onde de Broglie et l'énergie cinétique d'un électron libre qui se déplace à une vitesse de 0,75 c.
- Réponse
-
\(\lambda = 1.417 \, pm; \, K = 261.56 \, keV\)


