6.5 : Modèle de Bohr pour l'atome d'hydrogène
- Page ID
- 189629
À la fin de cette section, vous serez en mesure de :
- Expliquer la différence entre le spectre d'absorption et le spectre d'émission du rayonnement émis par les atomes
- Décrivez l'expérience de la feuille d'or de Rutherford et la découverte du noyau atomique
- Expliquer la structure atomique de l'hydrogène
- Décrire les postulats des débuts de la théorie quantique pour l'atome d'hydrogène
- Résumez comment le modèle quantique de Bohr de l'atome d'hydrogène explique le spectre de rayonnement de l'hydrogène atomique
Historiquement, le modèle de Bohr de l'atome d'hydrogène est le tout premier modèle de structure atomique qui explique correctement les spectres de rayonnement de l'hydrogène atomique. Le modèle occupe une place particulière dans l'histoire de la physique car il a introduit une théorie quantique précoce, qui a entraîné de nouveaux développements dans la pensée scientifique et a ensuite abouti au développement de la mécanique quantique. Pour comprendre les spécificités du modèle de Bohr, nous devons d'abord passer en revue les découvertes du XIXe siècle qui ont motivé sa formulation.
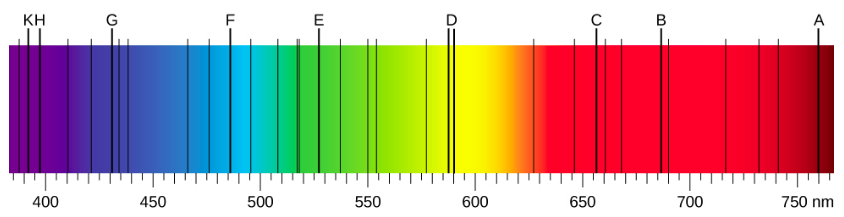
Lorsque nous utilisons un prisme pour analyser la lumière blanche provenant du soleil, plusieurs raies sombres sont observées dans le spectre solaire (Figure\(\PageIndex{1}\)). Les raies d'absorption solaire sont appelées raies de Fraunhofer, d'après Joseph von Fraunhofer, qui a mesuré avec précision leurs longueurs d'onde. Entre 1854 et 1861, Gustav Kirchhoff et Robert Bunsen ont découvert que, pour les différents éléments chimiques, le spectre d'émission de raies d'un élément correspond exactement à son spectre d'absorption linéaire. La différence entre le spectre d'absorption et le spectre d'émission est expliquée dans la figure\(\PageIndex{2}\).
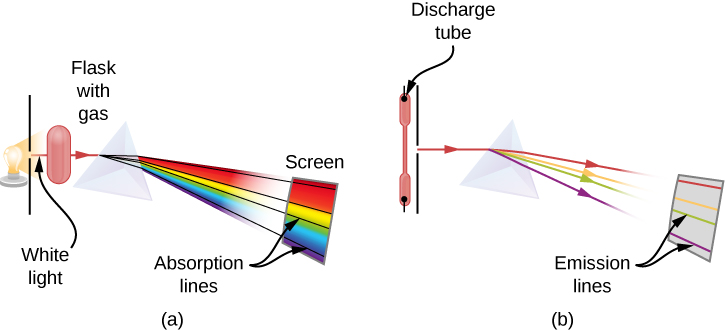
Un spectre d'absorption est observé lorsque la lumière traverse un gaz. Ce spectre apparaît sous forme de lignes noires qui apparaissent uniquement à certaines longueurs d'onde sur le fond du spectre continu de lumière blanche (Figure\(\PageIndex{2}\)). Les longueurs d'onde manquantes nous indiquent quelles longueurs d'onde du rayonnement sont absorbées par le gaz. Le spectre d'émission est observé lorsque de la lumière est émise par un gaz. Ce spectre est vu sous forme de lignes colorées sur fond noir (figures\(\PageIndex{3}\) et\(\PageIndex{4}\)). Les positions des raies d'émission nous indiquent quelles longueurs d'onde du rayonnement sont émises par le gaz. Chaque élément chimique possède son propre spectre d'émission caractéristique. Pour chaque élément, les positions de ses raies d'émission sont exactement les mêmes que celles de ses raies d'absorption. Cela signifie que les atomes d'un élément spécifique n'absorbent le rayonnement qu'à des longueurs d'onde spécifiques et que le rayonnement qui n'a pas ces longueurs d'onde n'est pas du tout absorbé par l'élément. Cela signifie également que le rayonnement émis par les atomes de chaque élément a exactement les mêmes longueurs d'onde que le rayonnement qu'ils absorbent.


Les spectres d'émission des éléments ont des structures complexes ; ils le deviennent encore plus pour les éléments dont le numéro atomique est élevé. Le spectre le plus simple, illustré sur la figure\(\PageIndex{4}\), appartient à l'atome d'hydrogène. Seules quatre lignes sont visibles à l'œil nu. Comme vous pouvez le lire de droite à gauche sur la Figure\(\PageIndex{4}\), ces lignes sont les suivantes : rouge (656 nm), appelée\(H-\alpha\) ligne ; aqua (486 nm), bleue (434 nm) et violette (410 nm). Les raies dont la longueur d'onde est inférieure à 400 nm apparaissent dans la partie ultraviolette du spectre (Figure\(\PageIndex{4}\), tout à gauche) et sont invisibles à l'œil nu. Il existe une infinité de raies spectrales invisibles dans la série pour l'hydrogène.
Une formule empirique pour décrire les positions (longueurs d'onde) λ des raies d'émission d'hydrogène de cette série a été découverte en 1885 par Johann Balmer. Elle est connue sous le nom de formule Balmer :
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - \dfrac{1}{n^2}\right). \label{balmer} \]
La constante\(R_H = 1.09737 \times 10^7 m^{-1}\) est appelée constante de Rydberg pour l'hydrogène. Dans l'équation \ ref {balmer}, l'entier positif n prend des valeurs\(n = 3, 4,5,6\) pour les quatre lignes visibles de cette série. La série de raies d'émission donnée par la formule de Balmer est appelée série de Balmer pour l'hydrogène. D'autres raies d'émission d'hydrogène découvertes au XXe siècle sont décrites par la formule de Rydberg, qui résume toutes les données expérimentales :
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{n_f^2} - \dfrac{1}{n_i^2}\right)\label{rydberg} \]
où\(n_i = n_f > n_i\) (en incréments entiers).
Quand\(n_f = 1\), la série de raies spectrales est appelée série Lyman. Lorsque\(n_f = 2\), la série est appelée série de Balmer, et dans ce cas, la formule de Rydberg coïncide avec la formule de Balmer (équation \ ref {balmer}). Quand\(n_f = 3\), la série s'appelle la série Paschen. Quand\(n_f = 4\), la série s'appelle la série Brackett. Quand\(n_f = 5\), la série s'appelle la série Pfund. Quand\(n_f = 6\), nous avons la série Humphreys. Comme vous pouvez le deviner, il existe une infinité de bandes spectrales de ce type dans le spectre de l'hydrogène, car il\(n_f\) peut s'agir de n'importe quel nombre entier positif.
La formule de Rydberg pour l'hydrogène donne les positions exactes des raies spectrales telles qu'elles sont observées en laboratoire ; cependant, au début du XXe siècle, personne ne pouvait expliquer pourquoi elle fonctionnait si bien. La formule de Rydberg est restée inexpliquée jusqu'à ce que le premier modèle réussi de l'atome d'hydrogène soit proposé en 1913.
Calculez les longueurs d'onde les plus longues et les plus courtes de la série Balmer.
Stratégie
Nous pouvons utiliser soit la formule de Balmer (équation \ ref {balmer}) soit la formule de Rydberg (équation \ ref {rydberg}). La longueur d'onde la plus longue est obtenue lorsque\(1/n_i\) i est le plus grand\(n_i = n_f + 1 = 3\), c'est-à-dire quand,\(n_f = 2\) pour la série Balmer. La plus petite longueur d'onde est obtenue quand elle\(1/n_i\) est la plus petite, c'est-à-dire\(1/n_i \rightarrow 0\) quand\(n_i \rightarrow \infty\).
Solution
La limite des ondes longues :
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - \dfrac{1}{3^2}\right) = (1.09737 \times 10^7) \dfrac{1}{m} \left( \dfrac{1}{4} - \dfrac{1}{9}\right) \Rightarrow \lambda = 656.3 \, nm \nonumber \]
La limite des ondes courtes :
\[ \dfrac{1}{\lambda} = R_H \left( \dfrac{1}{2^2} - 0\right) = (1.09737 \times 10^7) \dfrac{1}{m} \left( \dfrac{1}{4} \right) \Rightarrow \lambda = 364.6 \, nm. \nonumber \]
L'importance
Notez qu'il existe une infinité de raies spectrales situées entre ces deux limites.
Quelles sont les limites de la série Lyman ? Tu peux voir ces raies spectrales ?
- Réponse
-
121,5 nm et 91,1 nm ; non, ces bandes spectrales se situent dans l'ultraviolet
La clé pour percer le mystère des spectres atomiques réside dans la compréhension de la structure atomique. Les scientifiques savent depuis longtemps que la matière est composée d'atomes. Selon la science du XIXe siècle, les atomes sont les plus petites quantités indivisibles de matière. Cette croyance scientifique a été bouleversée par une série d'expériences révolutionnaires qui ont prouvé l'existence de particules subatomiques, telles que des électrons, des protons et des neutrons.
L'électron a été découvert et identifié comme étant la plus petite quantité de charge électrique par J.J. Thomson en 1897 lors de ses expériences sur les rayons cathodiques, également appelées expériences sur les rayons β : un rayon β est un faisceau d'électrons. En 1904, Thomson a proposé le premier modèle de structure atomique, connu sous le nom de modèle du « pudding aux prunes », dans lequel un atome était constitué d'une matière chargée positivement inconnue dans laquelle étaient incorporés des électrons négatifs, comme des prunes dans un pudding. Vers 1900, E. Rutherford et, indépendamment, Paul Ulrich Villard, ont classé tous les rayonnements connus à l'époque sous\(\alpha\) le nom de rayons,\(β\) de rayons et\(\gamma\) de rayons (un\(\gamma\) rayon est un faisceau de photons de haute énergie). En 1907, Rutherford et Thomas Royds ont utilisé des méthodes de spectroscopie pour montrer que les particules de\(\alpha\) rayonnement chargées positivement (appelées\(\alpha\) particules) sont en fait des atomes d'hélium doublement ionisés. En 1909, Rutherford, Ernest Marsden et Hans Geiger ont utilisé des\(\alpha\) particules dans leur célèbre expérience de diffusion qui a réfuté le modèle de Thomson (voir Momentum linéaire et collisions).
Lors de l'expérience sur la feuille d'or de Rutherford (également connue sous le nom d'expérience Geiger—Marsden), des particules α ont été incidentes sur une fine feuille d'or et ont été dispersées par des atomes d'or à l'intérieur de la feuille (voir Types de collisions). Les particules sortantes ont été détectées par un écran à scintillation à 360° entourant la cible en or (pour une description détaillée de la configuration expérimentale, voir Momentum linéaire et collisions). Lorsqu'une particule diffusée a heurté l'écran, un minuscule flash de lumière (scintillation) a été observé à cet endroit. En comptant les scintillations observées sous différents angles par rapport à la direction du faisceau incident, les scientifiques ont pu déterminer quelle fraction des particules incidentes était diffusée et quelle fraction n'avait pas été déviée du tout. Si le modèle du pudding aux prunes était correct, il n'y aurait pas de particules α rétrodiffusées. Cependant, les résultats de l'expérience de Rutherford ont montré que, bien qu'une fraction importante de particules α émerge de la feuille sans être du tout dispersées comme si la feuille ne les gênait pas, une fraction significative des particules α était rétrodiffusée vers la source. Ce type de résultat n'a été possible que lorsque la majeure partie de la masse et la totalité de la charge positive de l'atome d'or étaient concentrées dans un espace minuscule à l'intérieur de l'atome.
En 1911, Rutherford a proposé un modèle nucléaire de l'atome. Dans le modèle de Rutherford, un atome contenait un noyau chargé positivement de taille négligeable, presque comme un point, mais comprenant presque toute la masse de l'atome. L'atome contenait également des électrons négatifs situés à l'intérieur de l'atome mais relativement éloignés du noyau. Dix ans plus tard, Rutherford a inventé le nom de proton pour le noyau de l'hydrogène et le nom de neutron pour une particule hypothétique électriquement neutre qui médierait la liaison de protons positifs dans le noyau (le neutron a été découvert en 1932 par James Chadwick). Rutherford est crédité de la découverte du noyau atomique ; toutefois, le modèle de structure atomique de Rutherford n'explique pas la formule de Rydberg pour les raies d'émission d'hydrogène.
Le modèle de Bohr de l'atome d'hydrogène, proposé par Niels Bohr en 1913, a été le premier modèle quantique qui expliquait correctement le spectre d'émission d'hydrogène. Le modèle de Bohr combine la mécanique classique du mouvement planétaire avec le concept quantique des photons. Une fois que Rutherford a établi l'existence du noyau atomique, l'intuition de Bohr selon laquelle l'électron négatif de l'atome d'hydrogène doit tourner autour du noyau positif est devenue une conséquence logique de la loi de distance carrée inverse de l'attraction électrostatique. Rappelons que la loi de Coulomb décrivant l'attraction entre deux charges opposées a une forme similaire à la loi universelle de la gravitation de Newton en ce sens que la force gravitationnelle et la force électrostatique diminuent toutes deux au fur et à mesure que\(1/r^2\), où r est la distance de séparation entre les corps. . De la même manière que la Terre tourne autour du soleil, l'électron négatif de l'atome d'hydrogène peut tourner autour du noyau positif. Cependant, une charge accélératrice émet son énergie. Classiquement, si l'électron se déplaçait autour du noyau de façon planétaire, il subirait une accélération centripète et émettrait ainsi de l'énergie qui le ferait descendre en spirale dans le noyau. Un tel atome d'hydrogène planétaire ne serait pas stable, ce qui est contraire à ce que nous savons des atomes d'hydrogène ordinaires qui ne se désintègrent pas. De plus, le mouvement classique de l'électron ne permet pas d'expliquer le spectre d'émission discret de l'hydrogène.
Pour contourner ces deux difficultés, Bohr a proposé les trois postulats suivants du modèle de Bohr :
- L'électron négatif se déplace autour du noyau positif (proton) sur une orbite circulaire. Toutes les orbites des électrons sont centrées sur le noyau. Toutes les orbites classiquement possibles ne sont pas disponibles pour un électron lié au noyau.
- Les orbites électroniques autorisées satisfont à la première condition de quantification : sur la n ème orbite, le moment cinétique\(L_n\) de l'électron ne peut prendre que des valeurs discrètes :\[L_n = n\hbar, \, where \, n = 1,2,3, . . . \nonumber \] ce postulat indique que le moment cinétique de l'électron est quantifié. Désignée par\(r_n\) et\(v_n\), respectivement, le rayon de la n ième orbite et la vitesse de l'électron sur celle-ci, la première condition de quantification peut être exprimée explicitement comme\[m_ev_nr_n = n\hbar. \label{6.34} \]
- Un électron est autorisé à effectuer des transitions d'une orbite où se trouve son énergie\(E_n\) à une autre orbite où se trouve son énergie\(E_m\). Lorsqu'un atome absorbe un photon, l'électron effectue une transition vers une orbite de plus haute énergie. Lorsqu'un atome émet un photon, l'électron passe sur une orbite à faible énergie. Les transitions électroniques avec absorption ou émission de photons simultanées se produisent instantanément. Les transitions électroniques autorisées satisfont à la deuxième condition de quantification :\[hf = |E_n - E_m| \nonumber \] où\(hf\) est l'énergie d'un photon émis ou absorbé en fonction de la fréquence\(f\). La deuxième condition de quantification indique que le changement d'énergie d'un électron dans l'atome d'hydrogène est quantifié.
Ces trois postulats des débuts de la théorie quantique de l'atome d'hydrogène nous permettent de déduire non seulement la formule de Rydberg, mais également la valeur de la constante de Rydberg et d'autres propriétés importantes de l'atome d'hydrogène telles que ses niveaux d'énergie, son énergie d'ionisation et la taille des orbites électroniques. Notez que dans le modèle de Bohr, ainsi que deux postulats de quantification non classiques, nous avons également la description classique de l'électron en tant que particule soumise à la force de Coulomb, et son mouvement doit obéir aux lois du mouvement de Newton. L'atome d'hydrogène, en tant que système isolé, doit obéir aux lois de conservation de l'énergie et de la quantité de mouvement, comme le montre la physique classique. En gardant ce cadre théorique à l'esprit, nous sommes prêts à poursuivre notre analyse.
Orbites d'électrons
Pour obtenir la taille\(r_n\) des électrons sur l'orbite et leur vitesse\(v_n\), nous nous tournons vers la mécanique newtonienne. En tant que particule chargée, l'électron subit une attraction électrostatique vers le noyau chargé positivement au centre de son orbite circulaire. Cette attraction électrostatique est la force centripète qui fait que l'électron se déplace en cercle autour du noyau. Par conséquent, l'amplitude de la force centripète est identifiée à l'amplitude de la force électrostatique :
\[ \dfrac{m_ev_n^2}{r_n} = \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{r_n^2}. \label{6.36} \]
Ici,\(e\) indique la valeur de la charge élémentaire. L'électron négatif et le proton positif ont la même valeur de charge,
\[|q| = e. \nonumber \]
Lorsque l'équation \ ref {6.36} est combinée à la première condition de quantification donnée par l'équation \ ref {6.34}, nous pouvons résoudre pour la vitesse et pour le rayon\(r_n\) :\(v_n\)
\[v_n = \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{\hbar} \dfrac{1}{n} \label{6.37} \]
\[r_n = 4\pi \epsilon_0 \dfrac{\hbar^2}{m_ee^2}n^2. \label{6.38} \]
Notez que ces résultats nous indiquent que la vitesse de l'électron ainsi que le rayon de son orbite dépendent uniquement de l'indice n qui énumère l'orbite, car toutes les autres grandeurs des équations précédentes sont des constantes fondamentales. Nous voyons dans l'équation \ ref {6.38} que la taille de l'orbite augmente au carré de n. Cela signifie que la deuxième orbite est quatre fois plus grande que la première, et que la troisième orbite est neuf fois plus grande que la première, et ainsi de suite. Nous voyons également à partir de l'équation \ ref {6.37} que la vitesse de l'électron sur l'orbite diminue à mesure que la taille de l'orbite augmente. La vitesse de l'électron est maximale sur la première orbite de Bohr\(n = 1\), pour, qui est l'orbite la plus proche du noyau. Le rayon de la première orbite de Bohr est appelé rayon de Bohr de l'hydrogène, noté par\(a_0\). Sa valeur est obtenue\(n = 1\) en définissant dans l'équation \ ref {6.38} :
\[a_0 = 4\pi \epsilon_0 \dfrac{\hbar^2}{m_ee^2} = 5.29 \times 10^{-11} m = 0.529\space Å. \nonumber \]
Nous pouvons la remplacer\(a_0\) dans l'équation \ ref {6.38} pour exprimer le rayon de la n ème orbite en termes de\(a_0\) :
\[r_n = a_0n^2. \label{6.40} \]
Ce résultat signifie que les orbites des électrons dans l'atome d'hydrogène sont quantifiées parce que le rayon orbital ne prend que des valeurs spécifiques de\(a_0\)\(4a_0\),\(9a_0\),,\(16a_0\)... données par l'équation \ ref {6.40}, et aucune autre valeur n'est autorisée.
Energies électroniques
L'énergie totale\(E_n\) d'un électron sur la n ième orbite est la somme de son énergie cinétique\(K_n\) et de son énergie potentielle électrostatique\(U_n\). En utilisant l'équation \ ref {6.37}, nous trouvons que
\[K_n = \dfrac{1}{2}m_ev_n^2 = \dfrac{1}{32\pi^2 \epsilon^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.41} \]
Rappelons que l'énergie potentielle électrostatique d'interaction entre deux charges\(q_1\) séparées par une distance\(r_{12}\) est de\((1/4\pi \epsilon_0)q_1q_2/r_{12}\).\(q_2\) \(q_1 = +e\)Voici la charge du noyau dans l'atome d'hydrogène (la charge du proton),\(q_2 = -e\) la charge de l'électron et\(r_{12} = r_n\) le rayon de la n- ième orbite. Nous utilisons maintenant l'équation \ ref {6.38} pour déterminer l'énergie potentielle de l'électron :
\[U_n = - \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2}{r_n} = - \dfrac{1}{16\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.42} \]
L'énergie totale de l'électron est la somme de l'équation \ ref {6.41} et de l'équation \ ref {6.42} :
\[E_n = K_n + U_n = - \dfrac{1}{32\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} \dfrac{1}{n^2}. \label{6.43} \]
Notez que l'énergie dépend uniquement de l'indice n car les symboles restants dans l'équation \ ref {6.43} sont des constantes physiques. La valeur du facteur constant dans l'équation \ ref {6.43} est
\[E_0 = \dfrac{1}{32\pi^2 \epsilon_0^2} \dfrac{m_ee^4}{\hbar^2} = \dfrac{1}{8\epsilon_0^2} \dfrac{m_ee^4}{h^2} = 2.17 \times 10^{-18} J = 13.6 \, eV. \label{6.44} \]
Il est pratique d'exprimer l'énergie de l'électron sur la n ième orbite en termes de cette énergie, comme
\[E_n = -E_0 \dfrac{1}{n^2}. \label{6.45} \]
Nous pouvons maintenant voir que les énergies électroniques de l'atome d'hydrogène sont quantifiées car elles ne peuvent avoir que des valeurs discrètes\(-E_0, \, -E_0/4, \, -E_0/9, \, -E_0/16, . . . \) données par l'équation \ ref {6.45}, et aucune autre valeur énergétique n'est autorisée. Cet ensemble d'énergies électroniques autorisées est appelé spectre énergétique de l'hydrogène (Figure\(\PageIndex{5}\)). L'indice n qui énumère les niveaux d'énergie dans le modèle de Bohr est appelé nombre quantique d'énergie. Nous identifions l'énergie de l'électron à l'intérieur de l'atome d'hydrogène avec l'énergie de l'atome d'hydrogène. Notez que la plus petite valeur d'énergie est obtenue pour\(n = 1\), de sorte que l'atome d'hydrogène ne peut pas avoir une énergie inférieure à cela. Cette plus petite valeur de l'énergie électronique de l'atome d'hydrogène est appelée énergie fondamentale de l'atome d'hydrogène et sa valeur est
\[E_1 = −E_0 = −13.6 \, eV. \label{6.46} \]
L'atome d'hydrogène peut avoir d'autres énergies supérieures à l'état fondamental. Ces états énergétiques supérieurs sont appelés états énergétiques excités d'un atome d'hydrogène.
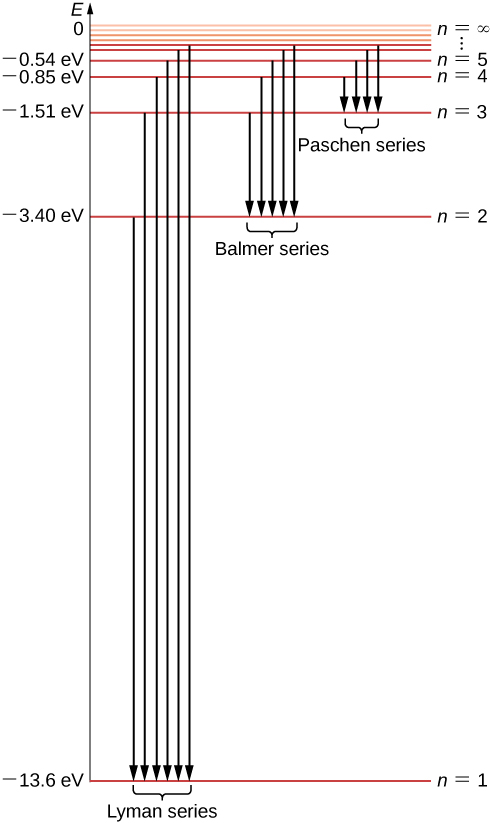
Il n'y a qu'un seul état fondamental, mais il existe une infinité d'états excités car il existe une infinité de valeurs de n dans l'équation \ ref {6.45}. Nous disons que l'électron est dans le « premier état excité » lorsque son énergie est\(E_n\) (quand\(n = 2\)), le deuxième état excité lorsque son énergie est\(E_3\) (quand\(n = 3\)) et, en général, dans le n ème état sorti lorsque son énergie l'est\(E_n + 1\). Il n'y a pas d'état excité le plus élevé de tous ; cependant, il y a une limite à la séquence des états excités. Si nous continuons\(n\) à augmenter dans l'équation \ ref {6.45}, nous trouvons que la limite est\(- lim_{n \rightarrow \infty} \, E_0/n^2 = 0\). Dans cette limite, l'électron n'est plus lié au noyau mais devient un électron libre. Un électron reste lié à l'atome d'hydrogène tant que son énergie est négative. Un électron qui tourne autour du noyau sur la première orbite de Bohr, la plus proche du noyau, se trouve à l'état fondamental, où son énergie a la plus faible valeur. À l'état fondamental, l'électron est le plus fortement lié au noyau et son énergie est donnée par l'équation \ ref {6.46}. Si nous voulons retirer cet électron de l'atome, nous devons lui fournir suffisamment d'énergie\(E_{\infty}\), pour au moins équilibrer son énergie fondamentale\(E_1\) :
\[E_{\infty} + E_1 = 0 \Rightarrow E_{\infty} = - E_1 = - (- E_0) = E_0 = 13.6 \, eV. \label{6.47} \]
L'énergie nécessaire pour retirer l'électron de l'atome est appelée énergie d'ionisation. L'énergie d'\(E_{\infty}\)ionisation nécessaire pour retirer l'électron de la première orbite de Bohr est appelée limite d'ionisation de l'atome d'hydrogène. La limite d'ionisation dans l'équation \ ref {6.47} que nous obtenons dans le modèle de Bohr correspond à la valeur expérimentale.
Lignes d'émission spectrales d'hydrogène
Pour obtenir les longueurs d'onde du rayonnement émis lorsqu'un électron passe de la n- ième orbite à la m -ième orbite, nous utilisons la deuxième des conditions de quantification de Bohr et l'équation \ ref {6.45} pour les énergies. L'émission d'énergie par l'atome ne peut se produire que lorsqu'un électron passe d'un état excité à un état d'énergie inférieure. Au cours d'une telle transition, le photon émis emporte la différence d'énergie entre les états impliqués dans la transition. La transition ne peut pas aller dans l'autre sens car l'énergie d'un photon ne peut pas être négative, ce qui signifie que pour l'émission, nous devons avoir\(E_n > E_m\) et\(n > m\). Par conséquent, le troisième des postulats de Bohr donne
\[\begin{align} hf &= |E_n - E_m| \nonumber \\[4pt] &= E_n - E_m \nonumber \\[4pt] &= -E_0 \dfrac{1}{n^2} + E_m \dfrac{1}{m^2} \nonumber \\[4pt] &= E_0 \left( \dfrac{1}{m^2} - \dfrac{1}{n^2} \right). \label{6.48} \end{align} \]
Nous exprimons maintenant l'énergie du photon en termes de longueur d'onde et divisons les deux côtés de l'équation \ ref {6.48} par\(hc\).\(hf = hc/\lambda\) Le résultat est
\[ \dfrac{1}{\lambda} = \dfrac{E_0}{hc} \left( \dfrac{1}{m^2} - \dfrac{1}{n^2} \right). \label{6.49} \]
La valeur de la constante dans cette équation est
\[\dfrac{E_0}{hc} = \dfrac{13.6 \, eV}{(4.136 \times 10^{-15} eV \cdot s)(2.997 \times 10^8 m/s)} = 1.097 \times 10^7 \dfrac{1}{m}. \label{6.50} \]
Cette valeur est exactement la constante de Rydberg\(R_H\) dans la formule heuristique de Rydberg Equation \ ref {rydberg}. En fait, l'équation \ ref {6.49} est identique à la formule de Rydberg, car pour un m donné, nous avons\(n = m + 1, \, m + 2, . . .\). Ainsi, le modèle quantique de Bohr de l'atome d'hydrogène nous permet de déduire la constante expérimentale de Rydberg à partir des principes de base et de l'exprimer en termes de constantes fondamentales. Les transitions entre les orbites électroniques autorisées sont illustrées sur la figure\(\PageIndex{5}\).
Nous pouvons répéter les mêmes étapes qui ont conduit à l'équation \ ref {6.49} pour obtenir la longueur d'onde du rayonnement absorbé ; cela donne à nouveau l'équation \ ref {6.49} mais cette fois pour les positions des raies d'absorption dans le spectre d'absorption de l'hydrogène. La seule différence est que, pour l'absorption, le nombre quantique\(m\) est l'indice de l'orbite occupée par l'électron avant la transition (orbite à basse énergie) et le nombre quantique\(n\) est l'indice de l'orbite vers laquelle l'électron effectue la transition (orbite à énergie plus élevée). La différence entre les énergies des électrons sur ces deux orbites est l'énergie du photon absorbé.
Si un atome d'hydrogène à l'état fondamental absorbe un photon de 93,7 nm, correspondant à une ligne de transition de la série Lyman, comment cela affecte-t-il l'énergie et la taille de l'atome ? Quelle quantité d'énergie est nécessaire pour ioniser l'atome lorsqu'il est dans cet état excité ? Donnez vos réponses en unités absolues et par rapport à l'état fondamental.
Stratégie
Avant l'absorption, l'atome est dans son état fondamental. Cela signifie que la transition des électrons a lieu de l'orbite\(m = 1\) vers un peu plus haut sur l'orbite. Tout d'abord, nous devons déterminer nn pour la longueur d'onde absorbée\(\lambda = 93.7 \, nm\). Ensuite, nous pouvons utiliser l'équation \ ref {6.45} pour trouver l'énergie\(E_n\) de l'état excité et son énergie d'ionisation\(E_{\infty,n}\), et utiliser l'équation \ ref {6.40} pour trouver le rayon\(r_n\) de l'atome à l'état excité. Pour estimer n, nous utilisons l'équation \ ref {6.49}.
Solution
Remplacez par\(m = 1\) λ = 93,7 nm dans l'équation \ ref {6,49} et résolvez par n. Vous ne devriez pas vous attendre à obtenir une réponse entière parfaite à cause d'erreurs d'arrondissement, mais votre réponse sera proche d'un entier, et vous pouvez estimer n en prenant la partie intégrale de votre réponse :
\[ \begin{align*} \dfrac{1}{\lambda} &= R_H \left( \dfrac{1}{1^1} - \dfrac{1}{n^2}\right) \\[4pt] \Rightarrow n &= \dfrac{1}{\sqrt{1 - \dfrac{1}{\lambda R_H}}} \\[4pt] &= \dfrac{1}{\sqrt{1 - \dfrac{1}{(93.7 \times 10^{−9}m)(1.097 \times 10^7 m^{−1})}}} \\[4pt] &= 6.07 \\[4pt] \Rightarrow n &= 6. \end{align*} \]
Le rayon de l'\(n = 6\)orbite est
\[r_n = a_0n^2= a_06^2 = 36a_0 = 36(0.529 \times 10^{−10} \, m) = 19.04 \times 10^{−10}\space m ≅ 19.0 \, Å. \nonumber \]
Ainsi, après absorption du photon de 93,7 nm, la taille de l'atome d'hydrogène à l'\(n = 6\)état excité est 36 fois plus grande qu'avant l'absorption, lorsque l'atome était à l'état fondamental. L'énergie du cinquième état excité (\(n = 6\)) est :
\[E_n = - \dfrac{E_0}{n^2} = - \dfrac{E_0}{6^2} = - \dfrac{E_0}{36} = - \dfrac{13.6 \, eV}{36} ≅ − 0.378 \, eV. \nonumber \]
Après absorption du photon de 93,7 nm, l'énergie de l'atome d'hydrogène est plus grande qu'elle ne l'était avant l'absorption. L'ionisation de l'atome lorsqu'il est dans le cinquième état excité (\(n = 6\)) nécessite 36 fois moins d'énergie que lorsque l'atome est à l'état fondamental :
\[E_{\infty,6} = -E_6 = -(-0.378 \, eV) = 0.378 \, eV. \nonumber \]
L'importance
Nous pouvons analyser n'importe quelle raie spectrale du spectre de l'hydrogène de la même manière. Ainsi, les mesures expérimentales des raies spectrales nous fournissent des informations sur la structure atomique de l'atome d'hydrogène.
Lorsqu'un électron d'un atome d'hydrogène se trouve dans son premier état excité, quelles sont les prévisions du modèle de Bohr concernant sa vitesse orbitale et son énergie cinétique ? Quelle est l'ampleur de son moment cinétique orbital ?
- Réponse
-
\(v_2 = 1.1 \times 10^6 m/s ≅0.0036 \, c;\)
\(L_2 = 2\hbar K_2 = 3.4 \, eV\)
Le modèle de Bohr de l'atome d'hydrogène prédit également correctement les spectres de certains ions semblables à l'hydrogène. Les ions de type hydrogène sont des atomes d'éléments dont le numéro atomique Z est supérieur à un (\(Z = 1\)pour l'hydrogène) mais dont tous les électrons sont retirés sauf un. Par exemple, un atome d'hélium électriquement neutre possède un numéro atomique\(Z = 2\). Cela signifie qu'il a deux électrons en orbite autour du noyau avec une charge de\(q = +Ze\). Lorsque l'un des électrons orbitaux est retiré de l'atome d'hélium (nous disons, lorsque l'atome d'hélium est ionisé individuellement), il reste une structure atomique semblable à de l'hydrogène où l'électron restant tourne autour du noyau avec une charge de\(q = +Ze\). Ce type de situation est décrit par le modèle de Bohr. En supposant que la charge du noyau ne soit pas\(+e\) mais\(+Ze\), nous pouvons répéter toutes les étapes, en commençant par l'équation \ ref {6.36}, pour obtenir les résultats pour un ion de type hydrogène :
\[r_n = \dfrac{a_0}{Z}n^2 \label{6.51} \]
où se\(a_0\) trouve l'orbite de Bohr de l'hydrogène, et
\[E_n = -Z^2E_0 \dfrac{1}{n^2} \label{6.52} \]
où\(E_0\) est la limite d'ionisation d'un atome d'hydrogène. Ces équations sont de bonnes approximations tant que le numéro atomique Z n'est pas trop grand.
Le modèle de Bohr est important car il s'agit du premier modèle à postuler la quantification des orbites d'électrons dans les atomes. Il s'agit donc d'une des premières théories quantiques qui ont donné le point de départ au développement de la théorie quantique moderne. Il a introduit le concept d'un nombre quantique pour décrire les états atomiques. La limite de la théorie quantique primitive est qu'elle ne peut pas décrire des atomes dans lesquels le nombre d'électrons en orbite autour du noyau est supérieur à un. Le modèle de Bohr de l'hydrogène est un modèle semi-classique car il combine le concept classique des orbites électroniques avec le nouveau concept de quantification. Le succès remarquable de ce modèle a incité de nombreux physiciens à chercher à expliquer pourquoi un tel modèle devrait fonctionner et à comprendre la physique qui sous-tend les postulats des débuts de la théorie quantique. Cette recherche a donné naissance à un tout nouveau concept d' « ondes de matière ».


