6.4 : L'effet Compton
- Page ID
- 189633
À la fin de cette section, vous serez en mesure de :
- Décrivez l'expérience de Compton
- Expliquer le décalage de longueur d'onde de Comp
- Décrire comment des expériences avec des rayons X confirment la nature particulaire du rayonnement
Deux des idées influentes d'Einstein introduites en 1905 étaient la théorie de la relativité spéciale et le concept d'un quantique de lumière, que nous appelons aujourd'hui photon. Au-delà de 1905, Einstein est allé plus loin en suggérant que les ondes électromagnétiques se propageant librement étaient constituées de photons qui sont des particules de lumière, au même titre que les électrons ou autres particules massives sont des particules de matière. Un faisceau de lumière monochromatique de longueur d'onde\(\lambda\) (ou, de manière équivalente, de fréquence\(f\)) peut être considéré soit comme une onde classique, soit comme un ensemble de photons qui se déplacent dans le vide à une seule vitesse\(c\) (la vitesse de la lumière), et qui transportent tous la même énergie\(E_f = hf\). Cette idée s'est révélée utile pour expliquer les interactions de la lumière avec les particules de matière.
Moment d'un photon
Contrairement à une particule de matière caractérisée par sa masse au repos\(m_0\), un photon est sans masse. Dans le vide, contrairement à une particule de matière qui peut varier de vitesse mais ne peut pas atteindre la vitesse de la lumière, un photon se déplace à une seule vitesse, qui est exactement la vitesse de la lumière. Du point de vue de la mécanique classique newtonienne, ces deux caractéristiques impliquent qu'un photon ne devrait pas exister du tout. Par exemple, comment déterminer le moment linéaire ou l'énergie cinétique d'un corps dont la masse est nulle ? Ce paradoxe apparent disparaît si l'on décrit un photon comme une particule relativiste. Selon la théorie de la relativité spéciale, toute particule de la nature obéit à l'équation énergétique relativiste
\[E^2 = p^2c^2 + m_0^2c^4. \label{6.17} \]
Cette relation peut également être appliquée à un photon. Dans l'équation \ ref {6.17},\(E\) est l'énergie totale d'une particule,\(p\) son moment linéaire et\(m_0\) sa masse de repos. Pour un photon, il suffit de définir\(m_0 = 0\) dans l'équation \ ref {6.17}, ce qui conduit à l'expression de la quantité\(p_f\) de mouvement d'un photon
\[p_f = \dfrac{E_f}{c}. \label{6.18} \]
Ici, l'énergie du photon\(E_f\) est la même que celle d'un quantum de fréquence de la lumière\(f\), que nous avons introduit pour expliquer l'effet photoélectrique :
\[E_f = hf = \dfrac{hc}{\lambda}. \label{6.19} \]
La relation d'onde qui relie la fréquence à la longueur\(f\) d'onde\(λ\) et à la vitesse vaut\(c\) également pour les photons :
\[\lambda f = c \label{6.20} \]
Par conséquent, un photon peut être caractérisé de manière équivalente soit par son énergie et sa longueur d'onde, soit par sa fréquence et sa quantité de mouvement. Les équations \ ref {6.19} et \ ref {6.20} peuvent être combinées dans la relation explicite entre le moment d'un photon et sa longueur d'onde :
\[p_f = \dfrac{h}{\lambda}. \label{6.21} \]
Notez que cette équation ne nous donne que l'amplitude de l'impulsion du photon et ne contient aucune information sur la direction dans laquelle le photon se déplace. Pour inclure la direction, il est habituel d'écrire l'impulsion du photon sous forme de vecteur :
\[\vec{p}_f = \hbar \vec{l}. \label{6.22} \]
Dans l'équation \ ref {6.22},\(\hbar = h/2\pi\) est la constante de Planck réduite (prononcée « h-bar »), qui est simplement la constante de Planck divisée par le facteur\(2\pi\). Le vecteur\(\vec{l}\) est appelé « vecteur d'onde » ou vecteur de propagation (la direction dans laquelle un photon se déplace). Le vecteur de propagation indique la direction du vecteur de moment linéaire du photon. L'amplitude du vecteur d'onde est
\[k = |\vec{k}| = 2\pi /\lambda \nonumber \]
et s'appelle le numéro d'onde. Notez que cette équation n'introduit aucune nouvelle physique. Nous pouvons vérifier que l'amplitude du vecteur dans l'équation \ ref {6.22} est la même que celle donnée par l'équation \ ref {6.18}.
L'effet Compton
L'effet Compton est le terme utilisé pour désigner un résultat inhabituel observé lorsque des rayons X sont diffusés sur certains matériaux. Selon la théorie classique, lorsqu'une onde électromagnétique est diffusée par des atomes, la longueur d'onde du rayonnement diffusé devrait être la même que la longueur d'onde du rayonnement incident. Contrairement à cette prédiction de la physique classique, les observations montrent que lorsque les rayons X sont diffusés par certains matériaux, tels que le graphite, les rayons X diffusés ont des longueurs d'onde différentes de la longueur d'onde des rayons X incidents. Ce phénomène classiquement inexplicable a été étudié expérimentalement par Arthur H. Compton et ses collaborateurs, et Compton a donné son explication en 1923.
Pour expliquer le changement des longueurs d'onde mesurées lors de l'expérience, Compton a utilisé l'idée d'Einstein selon laquelle la lumière est une particule. L'effet Compton occupe une place très importante dans l'histoire de la physique car il montre que le rayonnement électromagnétique ne peut pas être expliqué comme un phénomène purement ondulatoire. L'explication de l'effet Compton a fourni un argument convaincant à la communauté des physiques selon lequel les ondes électromagnétiques peuvent effectivement se comporter comme un flux de photons, ce qui a permis de placer le concept de photon sur des bases solides.
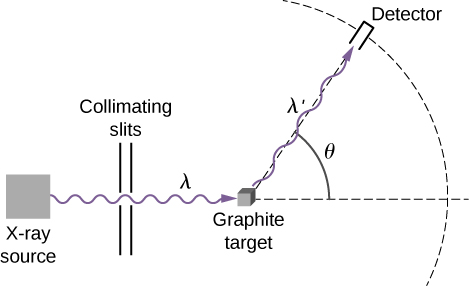
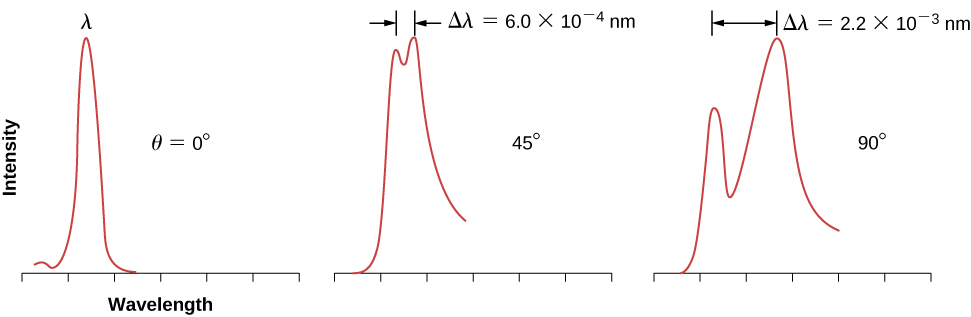
Les schémas de la configuration expérimentale de Compton sont présentés dans la figure\(\PageIndex{1}\). L'idée de l'expérience est simple : des rayons X monochromatiques de longueur d'onde\(λ\) sont incidents sur un échantillon de graphite (la « cible »), où ils interagissent avec les atomes à l'intérieur de l'échantillon ; ils émergent ensuite sous forme de rayons X diffusés de longueur d'onde\(λ'\). Un détecteur placé derrière la cible peut mesurer l'intensité du rayonnement diffusé dans n'importe quelle direction\(θ\) par rapport à la direction du faisceau de rayons X incident. Cet angle de diffusion,\(θ\), est l'angle entre la direction du faisceau diffusé et la direction du faisceau incident. Dans cette expérience, nous connaissons l'intensité et la longueur d'onde\(λ\) du faisceau entrant (incident) ; et pour un angle de diffusion donné\(θ\), nous mesurons l'intensité et la longueur\(λ'\) d'onde du faisceau sortant (diffusé). Les résultats typiques de ces mesures sont présentés sur la figure\(\PageIndex{2}\), où l'\(x\)axe -est la longueur d'onde des rayons X diffusés et l'\(y\)axe -est l'intensité des rayons X diffusés, mesurée pour différents angles de diffusion (indiqués sur les graphiques). Pour tous les angles de diffusion (sauf pour\(θ=0°\)), nous mesurons deux pics d'intensité. Un pic est situé à la longueur d'onde\(λ\), qui est la longueur d'onde du faisceau incident. L'autre pic est situé à une autre longueur d'onde,\(λ'\). Les deux pics sont séparés par\(Δλ\), ce qui dépend de l'angle\(θ\) de diffusion du faisceau sortant (dans le sens de l'observation). La séparation s'\(Δλ\)appelle le quart de travail de Compton.
Poste de travail Compton
Comme le donne Compton, l'explication du décalage de Compton est que dans le matériau cible, le graphite, les électrons de valence sont faiblement liés dans les atomes et se comportent comme des électrons libres. Compton a supposé que le rayonnement X incident est un flux de photons. Un photon entrant dans ce flux entre en collision avec un électron de valence dans la cible en graphite. Au cours de cette collision, le photon entrant transfère une partie de son énergie et de sa quantité de mouvement à l'électron cible et quitte la scène sous forme de photon diffusé. Ce modèle explique en termes qualitatifs pourquoi le rayonnement diffusé a une longueur d'onde plus longue que le rayonnement incident. En termes simples, un photon qui a perdu une partie de son énergie émerge sous la forme d'un photon de fréquence plus basse ou, de manière équivalente, d'une longueur d'onde plus longue. Pour montrer que son modèle était correct, Compton l'a utilisé pour dériver l'expression du décalage de Compton. Dans sa dérivation, il a supposé que le photon et l'électron sont des particules relativistes et que la collision obéit à deux principes de bon sens :
- la conservation de la quantité de mouvement linéaire et
- la conservation de l'énergie relativiste totale.
Dans la dérivation suivante du décalage de Compton,\(E_f\) et\(\vec{p}_f\) indiquent l'énergie et la quantité de mouvement, respectivement, d'un photon incident avec une fréquence\(f\). Le photon entre en collision avec un électron relativiste au repos, ce qui signifie qu'immédiatement avant la collision, l'énergie de l'électron est entièrement son énergie de masse restante\(m_0c^2\). Immédiatement après la collision, l'électron possède de l'énergie\(E\) et du moment\(\vec{p}\), qui répondent tous deux à l'équation \ ref {6.19}. Immédiatement après la collision, le photon sortant possède de l'énergie\(\vec{\tilde{E}}_f\), de la quantité de mouvement\(\vec{\tilde{p}}_f\) et de la fréquence\(f'\). La direction du photon incident est horizontale de gauche à droite, et la direction du photon sortant est angulaire\(θ\), comme illustré sur la figure\(\PageIndex{1}\). L'angle de diffusion\(θ\) est l'angle entre les vecteurs de moment\(\vec{p}_f\) et\(\vec{\tilde{p}}_f\), et nous pouvons écrire leur produit scalaire :
\[\vec{p} \cdot \vec{\tilde{p}}_f = p_f\vec{p}_f \cos \, \theta. \label{6.23} \]
Suivant l'argument de Compton, nous supposons que le photon et l'électron qui entrent en collision forment un système isolé. Cette hypothèse est valable pour les électrons faiblement liés qui, à une bonne approximation, peuvent être traités comme des particules libres. Notre première équation est la conservation de l'énergie pour le système photon-électron :
\[E_f + m_0c^2 = \tilde{E}_f + E. \label{6.24} \]
Le côté gauche de cette équation est l'énergie du système à l'instant précédant immédiatement la collision, et le côté droit de l'équation est l'énergie du système à l'instant immédiatement après la collision. Notre deuxième équation est la conservation du moment linéaire pour le système photon—électron où l'électron est au repos à l'instant précédant immédiatement la collision :
\[\vec{p}_f = \vec{\tilde{p}}_f + \vec{p}. \label{6.25} \]
Le côté gauche de cette équation est le moment du système juste avant la collision, et le côté droit de l'équation est le moment du système juste après la collision. Toute la physique de la diffusion Compton est contenue dans ces trois équations précédentes, le reste étant de l'algèbre. À ce stade, nous pourrions passer à la formule finale du décalage de Compton, mais il est utile de mettre en évidence les principales étapes algébriques qui mènent à la formule de Compton, que nous donnons ici comme suit.
Nous commençons par réarranger les termes de l'équation \ ref {6.24} et les mettre au carré :
\[[(E_f - \tilde{E}_f) + m_0c^2]^2 = E^2. \nonumber \]
À l'étape suivante, nous remplaçons l'équation \ ref {6.19} par\(E^2\), simplifions et divisons les deux côtés par\(c^2\) pour obtenir
\[(E_f / c - \tilde{E}_f / c)^2 + 2m_0c (E_f / c - \tilde{E}_f / c) = p^2. \nonumber \]
Nous pouvons maintenant utiliser l'équation \ ref {6.21} pour exprimer cette forme d'équation énergétique en termes de moments. Le résultat est
\[(p_f - \tilde{p}_f)^2 + 2m_0 c(p_f - \tilde{p}_f) = p^2. \label{6.26} \]
Pour éliminer\(p^2\), nous passons à l'équation de moment Equation \ ref {6.25}, nous réorganisons ses termes et la mettons au carré pour obtenir
\[ \begin{align*} (\vec{p}_f - \vec{\tilde{p}}_f)^2 &= p^2 \\[4pt] &= p_f^2 + \tilde{p}_f^2 - 2p_f \tilde{p}_f \, \cos \, \theta. \end{align*} \nonumber \]
Le produit des vecteurs de moment est donné par l'équation \ ref {6.23}. Lorsque nous substituons ce résultat\(p^2\) à l'équation \ ref {6.26}, nous obtenons l'équation d'énergie qui contient l'angle de diffusion θ :
\[(p_f - \tilde{p}_f)^2 + 2m_0c(p_f - \tilde{p}_f) = p_f^2 + \tilde{p}_f^2 - 2p_f \tilde{p}_f \, \cos \, \theta. \nonumber \]
Avec une algèbre plus poussée, ce résultat peut être simplifié en
\[\dfrac{1}{\tilde{p}_f} - \dfrac{1}{p_f} = \dfrac{1}{m_0c}(1 - \cos \, \theta). \label{6.27} \]
Maintenant, rappelez l'équation \ ref {6.21} et écrivez :\(1/\tilde{p}_f = \lambda' /h\) et\(1/p_f = \lambda /h\). Lorsque ces relations sont substituées dans l'équation \ ref {6.27}, nous obtenons la relation pour le décalage de Compton :
\[\lambda' - \lambda = \dfrac{h}{m_0c}(1 - \cos \, \theta). \label{6.28} \]
Le facteur\(h/m_0c\) est appelé la longueur d'onde Compton de l'électron :
\[\lambda_c = \dfrac{h}{m_0c} = 0.00243 \, nm = 2.43 \, pm. \label{6.29} \]
En désignant le décalage par\(\Delta \lambda = \lambda' - \lambda\), le résultat final peut être réécrit comme
\[\Delta \lambda = \lambda_c (1 - \cos \, \theta). \label{6.30} \]
Cette formule pour le décalage de Compton décrit remarquablement bien les résultats expérimentaux présentés dans la Figure\(\PageIndex{2}\). Les données de diffusion mesurées pour le molybdène, le graphite, la calcite et de nombreux autres matériaux cibles sont en accord avec ce résultat théorique. Le pic non décalé illustré sur la figure\(\PageIndex{1}\) est dû à des collisions de photons avec des électrons internes étroitement liés dans le matériau cible. Les photons qui entrent en collision avec les électrons internes des atomes cibles entrent en collision avec l'atome entier. Dans ce cas extrême, la masse restante dans l'équation \ ref {6.29} doit être remplacée par la masse restante de l'atome. Ce type de décalage est inférieur de quatre ordres de grandeur au décalage causé par les collisions avec des électrons et est si faible qu'il peut être négligé.
La diffusion Compton est un exemple de diffusion inélastique, dans laquelle le rayonnement diffusé a une longueur d'onde plus longue que la longueur d'onde du rayonnement incident. Dans l'usage actuel, le terme « diffusion Compton » est utilisé pour désigner la diffusion inélastique de photons par des particules libres et chargées. Dans la diffusion Compton, le fait de traiter les photons comme des particules dont les moments peuvent être transférés à des particules chargées fournit le contexte théorique permettant d'expliquer les changements de longueur d'onde mesurés dans les expériences ; cela prouve que le rayonnement est constitué de photons.
Une radiographie incidente à 71 pm est incidente sur une cible de calcite. Détermine la longueur d'onde du rayon X diffusé à un angle de 30°30°. Quel est le changement le plus important auquel on peut s'attendre dans le cadre de cette expérience ?
Stratégie
Pour trouver la longueur d'onde du rayon X diffusé, nous devons d'abord trouver le décalage de Compton pour l'angle de diffusion donné,\(\theta = 30°\). Nous utilisons l'équation \ ref {6.30}. On ajoute ensuite ce décalage à la longueur d'onde incidente pour obtenir la longueur d'onde diffusée. Le décalage Compton le plus important se produit à l'angle\(\theta\) où la valeur\(1 - \cos \, \theta\) est la plus élevée, c'est-à-dire pour l'angle\(\theta = 180°\).
Solution
Le changement à\(\theta = 30°\) est
\[\begin{align*} \Delta \lambda &= \lambda_c (1 - \cos \, 30°) \\[4pt] &= 0.134 \lambda_c \\[4pt] &= (0.134)(2.43) \, pm \\[4pt] &= 0.32 \end{align*} \nonumber \]
Cela donne la longueur d'onde diffusée :
\[\begin{align*} \lambda' &= \lambda + \Delta \lambda \\[4pt] &= (71 + 0.325) \, pm \\[4pt] &= 71.325 \,pm. \end{align*} \nonumber \]
Le changement le plus important est
\[\begin{align*} (\Delta \lambda )_{max} &= \lambda_c(1 − \cos \, 180°) \\[4pt] &= 2(2.43 \, pm) \\[4pt] &= 4.86 \, pm. \end{align*} \nonumber \]
L'importance
Le plus grand décalage de longueur d'onde est détecté pour le rayonnement rétrodiffusé ; cependant, la plupart des photons du faisceau incident traversent la cible et seule une petite fraction des photons est rétrodiffusée (généralement moins de 5 %). Ces mesures nécessitent donc des détecteurs très sensibles.
Une radiographie incidente à 71 pm est incidente sur une cible de calcite. Détermine la longueur d'onde du rayon X diffusé à un angle de 60°. Quel est le plus petit changement auquel on peut s'attendre dans le cadre de cette expérience ?
- Réponse
-
\((\Delta \lambda)_{min} = 0 \, m\)à un angle de 0° ;\(71.0 \, pm + 0.5 \lambda_c = 72.215 \, pm\)


