6.2 : Rayonnement du corps noir
- Page ID
- 189612
À la fin de cette section, vous serez en mesure de :
- Appliquez les lois de Wien et de Stefan pour analyser le rayonnement émis par un corps noir
- Expliquer l'hypothèse de Planck concernant les quanta énergétiques
Tous les corps émettent un rayonnement électromagnétique sur une gamme de longueurs d'onde. Dans un chapitre précédent, nous avons appris qu'un corps plus froid dégage moins d'énergie qu'un corps plus chaud. Nous savons également par observation que lorsqu'un corps est chauffé et que sa température augmente, la longueur d'onde perçue du rayonnement émis passe de l'infrarouge au rouge, puis du rouge à l'orange, et ainsi de suite. À mesure que sa température augmente, le corps brille avec des couleurs correspondant à des longueurs d'onde toujours plus petites du spectre électromagnétique. C'est le principe sous-jacent de l'ampoule à incandescence : un filament métallique chaud brille en rouge et, lorsque le chauffage se poursuit, sa lueur finit par couvrir toute la partie visible du spectre électromagnétique. La température (T) de l'objet qui émet un rayonnement, ou de l'émetteur, détermine la longueur d'onde à laquelle l'énergie rayonnée est maximale. Par exemple, le Soleil, dont la température de surface est comprise entre 5 000 K et 6 000 K, rayonne le plus fortement dans une gamme de longueurs d'onde d'environ 560 nm dans la partie visible du spectre électromagnétique. Votre corps, lorsqu'il est à sa température normale d'environ 300 K, rayonne le plus fortement dans la partie infrarouge du spectre.
Le rayonnement incident sur un objet est partiellement absorbé et partiellement réfléchi. À l'équilibre thermodynamique, la vitesse à laquelle un objet absorbe le rayonnement est la même que la vitesse à laquelle il l'émet. Par conséquent, un bon absorbeur de rayonnement (tout objet qui absorbe le rayonnement) est également un bon émetteur. Un absorbeur parfait absorbe tout le rayonnement électromagnétique qui lui arrive ; un tel objet est appelé corps noir.

Bien que le corps noir soit une idéalisation, étant donné qu'aucun objet physique n'absorbe 100 % du rayonnement incident, nous pouvons construire une réalisation rapprochée d'un corps noir sous la forme d'un petit trou dans la paroi d'une enceinte étanche connue sous le nom de radiateur à cavité, comme le montre la figure\(\PageIndex{1}\). Les parois intérieures d'un radiateur à cavité sont rugueuses et noircies, de sorte que tout rayonnement pénétrant par un petit trou dans la paroi de la cavité est piégé à l'intérieur de la cavité. À l'équilibre thermodynamique (à la température T), les parois de la cavité absorbent exactement autant de rayonnement qu'elles n'en émettent. De plus, à l'intérieur de la cavité, le rayonnement pénétrant dans le trou est équilibré par le rayonnement qui en sort. Le spectre d'émission d'un corps noir peut être obtenu en analysant la lumière émise par le trou. Les ondes électromagnétiques émises par un corps noir sont appelées rayonnement du corps noir.
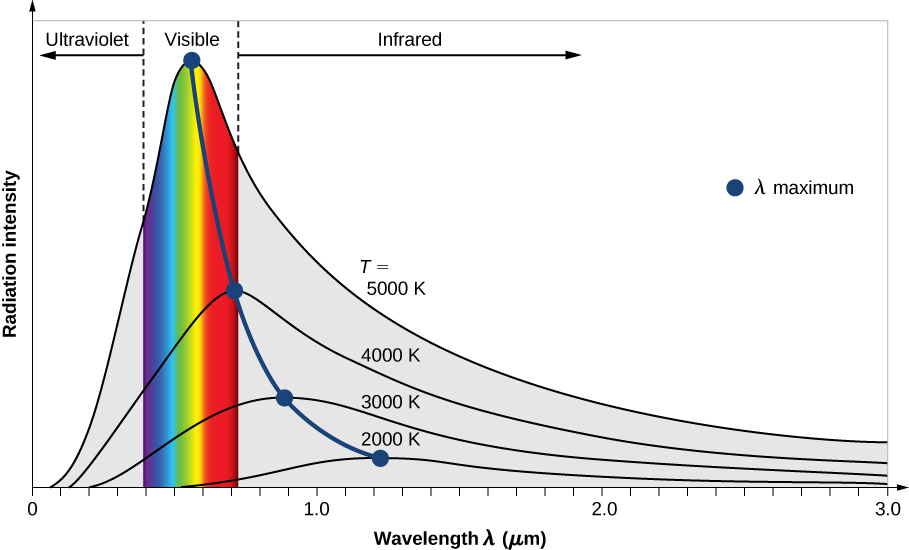
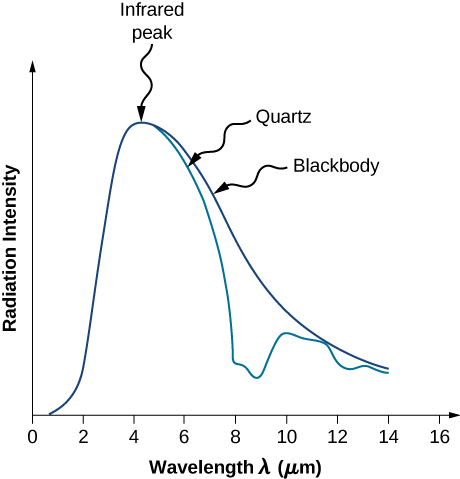
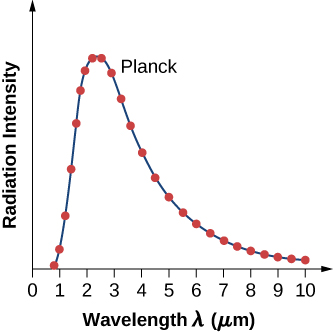
L'intensité\(I(\lambda, T)\) du rayonnement du corps noir dépend de la longueur\(\lambda\) d'onde du rayonnement émis et de la température T du corps noir (Figure\(\PageIndex{2}\)). La fonction\(I(\lambda, T)\) est l'intensité de puissance rayonnée par unité de longueur d'onde ; en d'autres termes, c'est la puissance rayonnée par unité de surface du trou dans un radiateur à cavité par unité de longueur d'onde. Selon cette définition,\(I(\lambda, T)d\lambda\) est la puissance par unité de surface émise dans l'intervalle de longueur d'onde de\(\lambda\) à\(\lambda + d\lambda\). La distribution de l'intensité entre les longueurs d'onde du rayonnement émis par les cavités a été étudiée expérimentalement à la fin du XIXe siècle. En général, le rayonnement émis par les matériaux ne suit qu'approximativement la courbe de rayonnement du corps noir (Figure\(\PageIndex{3}\)) ; cependant, les spectres des étoiles communes suivent de très près la courbe de rayonnement du corps noir.
Deux lois importantes résument les résultats expérimentaux du rayonnement du corps noir : la loi de déplacement de Wien et la loi de Stefan. La loi de déplacement de Wien est illustrée sur la figure\(\PageIndex{2}\) par la courbe reliant les maxima sur les courbes d'intensité. Sur ces courbes, nous voyons que plus le corps est chaud, plus la longueur d'onde correspondant au pic d'émission de la courbe de rayonnement est courte. Quantitativement, la loi de Vienne se lit comme suit :
\[\lambda_{max}T = 2.898 \times 10^{-3} m \cdot K \label{Wien} \]
où\(\lambda_{max}\) est la position du maximum sur la courbe de rayonnement. En d'autres termes,\(\lambda_{max}\) c'est la longueur d'onde à laquelle un corps noir rayonne le plus fortement à une température T donnée. Notez que dans l'équation \ ref {Wien}, la température est exprimée en kelvins. La loi de déplacement de Wien nous permet d'estimer la température des étoiles éloignées en mesurant la longueur d'onde du rayonnement qu'elles émettent.
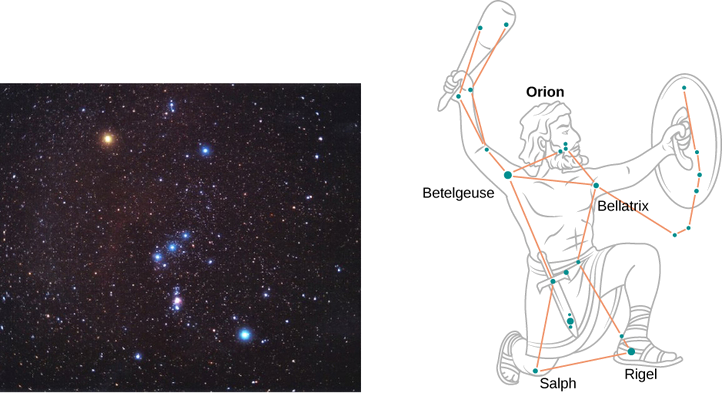
Par temps clair pendant les mois d'hiver, si vous vous trouvez dans l'hémisphère nord et que vous regardez le ciel, vous pouvez voir la constellation d'Orion (Le Chasseur). Une étoile de cette constellation, Rigel, scintille en bleu et une autre étoile, Bételgeuse, a une couleur rougeâtre, comme le montre la figure\(\PageIndex{4}\). Laquelle de ces deux étoiles est la plus cool, Bételgeuse ou Rigel ?
Stratégie
Nous traitons chaque étoile comme un corps noir. Ensuite, selon la loi de Vienne, sa température est inversement proportionnelle à la longueur d'onde de son intensité maximale. La longueur d'onde\(\lambda_{max}^{(blue)}\) de la lumière bleue est plus courte que la longueur d'onde\(\lambda_{max}^{(red)}\) de la lumière rouge. Même si nous ne connaissons pas les longueurs d'onde précises, nous pouvons tout de même définir une proportion.
Solution
En écrivant la loi de Vienne pour l'étoile bleue et pour l'étoile rouge, nous avons
\[\begin {align*} \lambda_{max}^{(red)}T_{(red)} &= 2.898 \times 10^{-3} m \cdot K \\[5pt] &= \lambda_{max}^{(blue)} T_{(blue)} \end{align*} \nonumber \]
Une fois simplifié, cela donne
\[T_{(red)} = \dfrac{\lambda_{max}^{(blue)}}{\lambda_{max}^{(red)}}T_{(blue)} < T_{(blue)} \nonumber \]
Par conséquent, Bételgeuse est plus fraîche que Rigel.
L'importance
Notez que la loi de déplacement de Wien nous indique que plus la température d'un corps émetteur est élevée, plus la longueur d'onde du rayonnement qu'il émet est courte. L'analyse qualitative présentée dans cet exemple est généralement valable pour tout corps émetteur, qu'il s'agisse d'un objet de grande taille tel qu'une étoile ou d'un petit objet tel que le filament incandescent d'une ampoule à incandescence.
La flamme d'une bougie parfumée à la pêche est de couleur jaunâtre et celle d'un brûleur de Bunsen dans un laboratoire de chimie a une couleur bleutée. Quelle flamme a une température plus élevée ?
- Réponse
La deuxième relation expérimentale est la loi de Stefan, qui concerne la puissance totale du rayonnement du corps noir émis sur l'ensemble du spectre des longueurs d'onde à une température donnée. Dans\(\PageIndex{2}\), cette puissance totale est représentée par l'aire située sous la courbe de rayonnement du corps noir pour un T donné. Lorsque la température d'un corps noir augmente, la puissance totale émise augmente également. Quantitativement, la loi de Stefan exprime cette relation comme
\[P(T) = \sigma AT^4 \nonumber \]
où\(A\) est la surface d'un corps noir,\(T\) sa température (en kelvins) et\(σ\) la constante de Stefan—Boltzmann,\(\sigma = 5.670 \times 10^{-8} W/(m^2 \cdot K^4)\). La loi de Stefan nous permet d'estimer la quantité d'énergie émise par une étoile en mesurant sa température à distance.
Une étoile telle que notre Soleil finira par évoluer vers une étoile « géante rouge », puis vers une étoile « naine blanche ». Une naine blanche typique a à peu près la taille de la Terre et sa température de surface est d'environ\(2.5 \times 10^4 K\). Une géante rouge typique a une température de surface\(3.0 \times 10^3 K\) et un rayon environ 100 000 fois plus grands que ceux d'une naine blanche. Quelle est la puissance moyenne rayonnée par unité de surface et la puissance totale rayonnée par chacun de ces types d'étoiles ? Comment se comparent-ils ?
Stratégie
Si nous traitons l'étoile comme un corps noir, alors selon la loi de Stefan, la puissance totale émise par l'étoile est proportionnelle à la quatrième puissance de sa température. Pour déterminer la puissance rayonnée par unité de surface, il n'est pas nécessaire de faire d'hypothèses sur la forme de l'étoile car P/A dépend uniquement de la température. Cependant, pour calculer la puissance totale, nous devons supposer que l'énergie rayonne à travers une surface sphérique entourant l'étoile, de sorte que la surface est\(A = 4\pi R^2\), où R est son rayon.
Solution
Une simple proportion basée sur la loi de Stefan donne
\[\dfrac{P_{dwarf}/A_{dwarf}}{P_{giant}/A_{giant}} = \dfrac{\sigma T_{dwarf}^4}{\sigma T_{giant}^4} = \left(\dfrac{T_{dwarf}}{T_{giant}}\right)^4 = 4820 \label{6.5} \]
La puissance émise par unité de surface par une naine blanche est environ 5 000 fois supérieure à la puissance émise par une géante rouge. En désignant ce ratio par\(a=4.8×10^3\), l'équation \ ref {6.5} donne
\[\dfrac{P_{dwarf}}{P_{giant}} = \alpha \dfrac{A_{dwarf}}{A_{giant}} = \alpha \dfrac{4\pi R_{dwarf}^2}{4\pi R_{giant}^2} = \alpha \left( \dfrac{R_{dwarf}}{R_{giant}} \right)^2 = 4.8 \times 10^{−7} \nonumber \]
Nous voyons que la puissance totale émise par une naine blanche ne représente qu'une infime fraction de la puissance totale émise par une géante rouge. Malgré sa température relativement plus basse, la puissance globale émise par une géante rouge dépasse de loin celle de la naine blanche, car la géante rouge a une superficie beaucoup plus grande. Pour estimer la valeur absolue de la puissance émise par unité de surface, nous utilisons à nouveau la loi de Stefan. Pour la naine blanche, on obtient
\[\dfrac{P_{dwarf}}{A_{dwarf}} = \sigma T_{dwarf}^4 = 5.670 \times 10^{-8} \dfrac{W}{m^2 \cdot K^4} (2.5 \times 10^4 \, K)^4 = 2.2 \times 10^{10} \dfrac{W}{m^2} \label{6.7} \]
Le résultat analogue pour la géante rouge est obtenu en redimensionnant le résultat pour une naine blanche :
\[\dfrac{P_{giant}}{A_{giant}} = \dfrac{2.2 \times 10^{10}}{4.82 \times 10^3} \dfrac{W}{m^2} = 4.56 \times 10^6 \dfrac{W}{m^2} \cong 4.6 \times 10^{-6} \dfrac{W}{m^2} \nonumber \]
L'importance
Pour estimer la puissance totale émise par une naine blanche, nous pouvons en principe utiliser l'équation \ ref {6.7}. Cependant, pour trouver sa surface, il faut connaître le rayon moyen, ce qui n'est pas donné dans cet exemple. La solution s'arrête donc là. Il en va de même pour l'étoile géante rouge.
Un tisonnier est en train d'être chauffé. À mesure que sa température augmente, le tisonnier commence à briller, d'abord d'un rouge terne, puis d'un rouge vif, puis d'un orange et enfin d'un jaune. Utilisez la courbe de rayonnement du corps noir ou la loi de Wien pour expliquer ces changements de couleur de la lueur.
- Réponse
-
La longueur d'onde maximale du rayonnement diminue avec l'augmentation de la température.
Supposons que deux étoiles,\(α\) et\(β\), rayonnent exactement de la même puissance totale. Si le rayon de l'étoile\(α\) est trois fois supérieur à celui de l'étoile\(β\), quel est le rapport des températures de surface de ces étoiles ? Lequel est le plus chaud ?
- Réponse
-
\(T_{\alpha}/T_{\beta} = 1/\sqrt{3} \cong 0.58\), donc l'étoile\(\beta\) est plus chaude.
Le terme « corps noir » a été inventé par Gustav R. Kirchhoff en 1862. La courbe de rayonnement du corps noir était connue expérimentalement, mais sa forme a échappé à toute explication physique jusqu'en 1900. Le modèle physique d'un corps noir à la température T est celui des ondes électromagnétiques enfermées dans une cavité (Figure\(\PageIndex{1}\)) et en équilibre thermodynamique avec les parois de la cavité. Les vagues peuvent échanger de l'énergie avec les parois. L'objectif ici est de déterminer la distribution de la densité d'énergie entre les différents modes de vibration à différentes longueurs d'onde (ou fréquences). En d'autres termes, nous voulons savoir quelle quantité d'énergie est transportée par une seule longueur d'onde ou une bande de longueurs d'onde. Une fois que nous connaissons la distribution de l'énergie, nous pouvons utiliser des méthodes statistiques standard (similaires à celles étudiées dans un chapitre précédent) pour obtenir la courbe de rayonnement du corps noir, la loi de Stefan et la loi de déplacement de Wien. Lorsque le modèle physique est correct, les prédictions théoriques doivent être les mêmes que les courbes expérimentales.
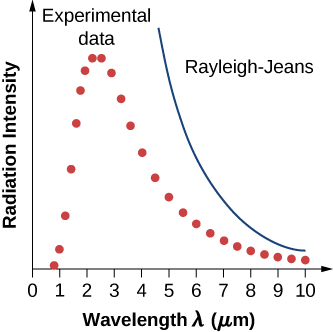
Dans une approche classique du problème du rayonnement du corps noir, dans laquelle le rayonnement est traité comme des ondes (comme vous l'avez étudié dans les chapitres précédents), les modes des ondes électromagnétiques piégées dans la cavité sont en équilibre et échangent continuellement leur énergie avec les parois de la cavité. Il n'y a aucune raison physique pour qu'une onde fasse autrement : n'importe quelle quantité d'énergie peut être échangée, soit en étant transférée de l'onde au matériau de la paroi, soit en étant reçue par l'onde depuis le matériau de la paroi. Ce tableau classique est à la base du modèle développé par Lord Rayleigh et, indépendamment, par Sir James Jeans. Le résultat de ce modèle classique des courbes de rayonnement du corps noir est connu sous le nom de loi de Rayleigh—Jeans. Cependant, comme le montre la figure\(\PageIndex{5}\), la loi de Rayleigh—Jeans ne parvient pas à reproduire correctement les résultats expérimentaux. Dans la limite des courtes longueurs d'onde, la loi de Rayleigh—Jeans prédit une intensité de rayonnement infinie, ce qui est incompatible avec les résultats expérimentaux selon lesquels l'intensité du rayonnement a des valeurs finies dans la région ultraviolette du spectre. Cette divergence entre les résultats de la théorie classique et ceux des expériences, que l'on a appelé la catastrophe ultraviolette, montre que la physique classique ne parvient pas à expliquer le mécanisme du rayonnement des corps noirs.
Le problème du rayonnement du corps noir a été résolu en 1900 par Max Planck. Planck a utilisé la même idée que le modèle Rayleigh—Jeans en ce sens qu'il a traité les ondes électromagnétiques entre les parois de la cavité de manière classique et a supposé que le rayonnement est en équilibre avec les parois de la cavité. L'idée novatrice que Planck a introduite dans son modèle est l'hypothèse que le rayonnement de la cavité provient d'oscillations atomiques à l'intérieur des parois de la cavité, et que ces oscillations ne peuvent avoir que des valeurs d'énergie discrètes. Par conséquent, le rayonnement piégé à l'intérieur des parois de la cavité ne peut échanger de l'énergie avec les parois qu'en quantités discrètes. L'hypothèse de Planck concernant les valeurs d'énergie discrètes, qu'il a appelée quanta, suppose que les oscillateurs situés à l'intérieur des parois de la cavité ont des énergies quantifiées. C'était une idée toute nouvelle qui allait au-delà de la physique classique du XIXe siècle car, comme vous l'avez appris dans un chapitre précédent, dans le tableau classique, l'énergie d'un oscillateur peut prendre n'importe quelle valeur continue. Planck a supposé que l'énergie d'un oscillateur (\(E_n\)) ne peut avoir que des valeurs discrètes ou quantifiées :
\[E_n = nhf, \, where \, n = 1,2,3, \ldots \label{eq30} \]
Dans l'équation \ ref {eq30},\(f\) est la fréquence de l'oscillateur de Planck. Le nombre naturel\(n\) qui énumère ces énergies discrètes est appelé nombre quantique. La constante physique\(h\) est appelée constante de Planck :
\[h = 6.626 \times 10^{-34} J \cdot s = 4.136 \times 10^{-15} eV \cdot s \label{6.10} \]
Chaque valeur d'énergie discrète correspond à un état quantique d'un oscillateur de Planck. Les états quantiques sont énumérés par des nombres quantiques. Par exemple, lorsque l'oscillateur de Planck est dans son premier état\(n 1\) quantique, son énergie l'est\(E_1 = hf\) ; lorsqu'il est dans l'état\(n = 2\) quantique, son énergie l'est\(E_2 = 2hf\) ; lorsqu'il est dans l'état\(n = 3\) quantique,\(E_3 = 3hf\) etc.
Notez que l'équation \ ref {eq30} montre qu'il existe une infinité d'états quantiques, qui peuvent être représentés par une séquence {hf, 2 hf, 3 hf,..., (n — 1) hf, nhf, (n + 1) hf, (n + 1) hf,...}. Chacun des deux états quantiques consécutifs de cette séquence est séparé par un saut d'énergie,\(\delta E = hf\). Un oscillateur situé dans la paroi peut recevoir de l'énergie du rayonnement dans la cavité (absorption) ou transmettre de l'énergie au rayonnement dans la cavité (émission). Le processus d'absorption envoie l'oscillateur vers un état quantique supérieur, et le processus d'émission envoie l'oscillateur vers un état quantique inférieur. Quel que soit le sens de cet échange d'énergie, la plus petite quantité d'énergie pouvant être échangée est hf. Il n'y a pas de limite supérieure à la quantité d'énergie qui peut être échangée, mais ce qui est échangé doit être un multiple entier de hf. Si le paquet d'énergie n'a pas cette quantité exacte, il n'est ni absorbé ni émis par la paroi du corps noir.
L'hypothèse des quanta d'énergie de Planck indique que la quantité d'énergie émise par l'oscillateur est transportée par le quantum du rayonnement,\(\Delta E\) :
\[\Delta E = hf \label{planck} \]
Rappelons que la fréquence du rayonnement électromagnétique est liée à sa longueur d'onde et à la vitesse de la lumière par la relation fondamentale\(f\lambda = c\). This means that we can express Équation \ ref {6.10} de manière équivalente en termes de longueur d'onde.\(\lambda\). When included in the computation of the energy density of a blackbody, Planck’s hypothesis gives the following theoretical expression for the power intensity of emitted radiation per unit wavelength:
\[I(\lambda, T) = \dfrac{2\pi hc^2}{\lambda^5} \dfrac{1}{e^{hc/\lambda k_BT} - 1} \label{6.11} \]
où c est la vitesse de la lumière dans le vide et kBkB est la constante de Boltzmann,\(k_B = 1.380 \times 10^{-23} J/K\). La formule théorique exprimée dans l'équation \ ref {6.11} est appelée loi de rayonnement du corps noir de Planck. Cette loi est en accord avec la courbe expérimentale de rayonnement du corps noir (Figure\(\PageIndex{2}\)). De plus, la loi de déplacement de Wien et la loi de Stefan peuvent toutes deux être dérivées de l'équation \ ref {6.11}. Pour dériver la loi de déplacement de Wien, nous utilisons le calcul différentiel pour déterminer le maximum de la courbe d'intensité du rayonnement\(I(\lambda, T)\). Pour dériver la loi de Stefan et trouver la valeur de la constante de Stefan—Boltzmann, nous utilisons le calcul intégral et l'intégrons\(I(\lambda, T)\) pour trouver la puissance totale rayonnée par un corps noir à une température dans tout le spectre des longueurs d'onde allant de\(\lambda = 0\) à\(\lambda = \infty\). Cette dérivation fera l'objet d'un exercice plus loin dans ce chapitre.
Un oscillateur quantique dans la paroi de la cavité de la\(\PageIndex{1}\) figure vibre à une fréquence de\(5.0 \times 10^{14} Hz\). Calculez l'espacement entre ses niveaux d'énergie.
Stratégie
Les états énergétiques d'un oscillateur quantique sont donnés par l'équation \ ref {eq30}. L'espacement énergétique\(\Delta E\) est obtenu en déterminant la différence d'énergie entre deux états quantiques adjacents pour les nombres quantiques n + 1 et n.
Solution
Nous pouvons substituer la fréquence donnée et la constante de Planck directement dans l'équation :
\[\begin {align*} \Delta E &= E_{n + 1} − En = (n + 1)hf − nhf \\[5pt] &= hf \\[5pt] &= (6.626 \times 10^{−34} \, J \cdot s)(5.0 \times 10^{14} \, Hz) \\[5pt] &= 3.3 \times 10^{− 19} \, J \end{align*} \nonumber \]
L'importance
Notez que nous ne précisons pas quel type de matériau a été utilisé pour construire la cavité. Ici, un oscillateur quantique est un modèle théorique d'un atome ou d'une molécule de matériau dans la paroi.
Une molécule vibre à une fréquence de\(5.0 \times 10^{14}\, Hz\). Quel est le plus petit écart entre ses niveaux d'énergie vibratoire ?
- Réponse
-
\(3.3 \times 10^{-19} J\)
Une masse de 1,0 kg oscille à l'extrémité d'un ressort avec une constante de ressort de 1 000 N/m. L'amplitude de ces oscillations est de 0,10 m. Utilisez le concept de quantification pour déterminer l'espacement énergétique de cet oscillateur classique. La quantification de l'énergie est-elle significative pour les systèmes macroscopiques tels que cet oscillateur ?
Stratégie
Nous utilisons l'équation \ ref {planck} comme si le système était un oscillateur quantique, mais avec la fréquence f de la masse qui vibre sur un ressort. Pour évaluer si la quantification a un effet significatif ou non, nous comparons l'espacement des énergies quantiques à l'énergie totale macroscopique de cet oscillateur classique.
Solution
Pour la constante de ressort\(k = 1.0 \times 10^3 N/m\), la fréquence f de la masse,\(m = 1.0 \, kg\), est
\[f = \dfrac{1}{2\pi} \sqrt{\dfrac{k}{m}} = \dfrac{1}{2\pi} \sqrt{\dfrac{1.0 \times 10^3 N/m}{1.0 \, kg}} \simeq 5.0 \, Hz \nonumber \]
Le quantum d'énergie qui correspond à cette fréquence est
\[\Delta E = hf = (6.626 \times 10^{-34} J \cdot s)(5.0 \, Hz) = 3.3 \times 10^{-33} J \nonumber \]
Lorsque les vibrations ont une amplitude\(A = 0.10 \, m\), l'énergie des oscillations est
\[E = \dfrac{1}{2} kA^2 = \dfrac{1}{2}(1000 \, N/m)(0.1 \, m)^2 = 5.0 \, J \nonumber \]
L'importance
Ainsi, pour un oscillateur classique, nous avons\(\Delta E/E \approx 10^{-34}\). Nous constatons que la séparation des niveaux d'énergie est incommensurablement faible. Par conséquent, à toutes fins pratiques, l'énergie d'un oscillateur classique prend des valeurs continues. C'est pourquoi les principes classiques peuvent être appliqués aux systèmes macroscopiques rencontrés dans la vie quotidienne sans perte de précision.
Le résultat de l'exemple\(\PageIndex{4}\) serait-il différent si la masse n'était pas de 1,0 kg mais une masse minuscule de 1,0 µ g et que l'amplitude des vibrations était de 0,10 µm ?
- Réponse
-
Non, parce qu'alors\(\Delta E /E \approx 10^{-21}\)
Lorsque Planck a publié ses résultats pour la première fois, l'hypothèse des quanta énergétiques n'a pas été prise au sérieux par la communauté des physiciens car elle ne découlait d'aucune théorie physique établie à l'époque. Elle a été perçue, même par Planck lui-même, comme une astuce mathématique utile qui a permis de bien « ajuster » théoriquement la courbe expérimentale. Cette perception a changé en 1905 lorsqu'Einstein a publié son explication de l'effet photoélectrique, dans laquelle il a donné un nouveau sens au quantum énergétique de Planck : celui d'une particule de lumière.


