Skip to main content
Global

5.7 : Pratique du chapitre

  1. Last updated
  2. Save as PDF
  • Page ID
    191673

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    5.1 Propriétés des fonctions de densité de probabilité continues

    1.

    Quel type de distribution le graphique illustre-t-il ?

    L'axe horizontal est compris entre 0 et 10. La distribution est modélisée par un rectangle s'étendant de x = 3 à x =8.

    Figurine\(\PageIndex{23}\)

    2.

    Quel type de distribution le graphique illustre-t-il ?

    Ce graphique présente une pente descendante. Il commence à un point de l'axe Y et s'approche de l'axe des X sur le bord droit du graphique.

    Figurine\(\PageIndex{24}\)

    3.

    Quel type de distribution le graphique illustre-t-il ?

    Ce graphique montre un graphique en forme de cloche. Le graphique symétrique atteint sa hauteur maximale à x = 0 et s'incline progressivement vers le bas jusqu'à l'axe X de chaque côté du pic.

    Figurine\(\PageIndex{25}\)

    4.

    Que représente la zone ombrée ? \(P\)(___\(< x <\) ___)

    Ce graphique montre une distribution uniforme. L'axe horizontal est compris entre 0 et 10. La distribution est modélisée par un rectangle s'étendant de x = 1 à x = 8. Une région comprise entre x = 2 et x = 5 est ombrée à l'intérieur du rectangle.

    Figurine\(\PageIndex{26}\)

    5.

    Que représente la zone ombrée ? \(P\)(___\(< x <\) ___)

    Ce graphique montre une distribution exponentielle. Le graphique présente une pente descendante. Il commence à un point de l'axe Y et s'approche de l'axe des X sur le bord droit du graphique. La région située sous le graphique, de x = 6 à x = 7, est ombrée.

    Figurine\(\PageIndex{27}\)

    6.

    Pour une distribution de probabilité continue,\(0 \leq x \leq 15\). Qu'\(P(x > 15)\)est-ce que c'est

    7.

    Quelle est la surface sous laquelle se trouve la fonction\(f(x)\) si la fonction est une fonction de densité de probabilité continue ?

    8.

    Pour une distribution de probabilité continue,\(0 \leq x \leq 10\). Qu'\(P(x = 7)\)est-ce que c'est

    9.

    Une fonction de probabilité continue est limitée à la partie comprise entre\(x = 0\) et\(7\). Qu'\(P(x = 10)\)est-ce que c'est

    10.

    \(f(x)\)car une fonction de probabilité continue est\(\frac{1}{5}\), et la fonction est limitée à\(0 \leq x \leq 5\). Qu'\(P(x < 0)\)est-ce que c'est

    11.

    \(f(x)\), une fonction de probabilité continue, est égale à\(\frac{1}{12}\), et la fonction est limitée à\(0 \leq x \leq 12\). Qu'\(P(0 < x < 12)\)est-ce que c'est

    12.

    Déterminez la probabilité qui\(x\) se situe dans la zone ombrée.

    Figurine\(\PageIndex{28}\)

    13.

    Déterminez la probabilité qui\(x\) se situe dans la zone ombrée.

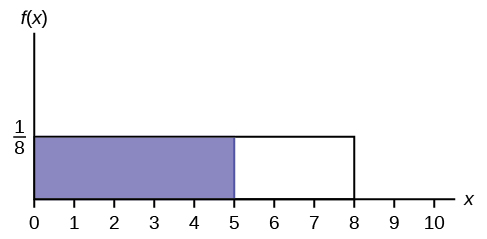    902063719447ede776b3c000cae81c74ed9c2ff5 (1) .jpg
    Figurine\(\PageIndex{29}\)

    14.

    Déterminez la probabilité qui\(x\) se situe dans la zone ombrée.

    Figurine\(\PageIndex{30}\)

    15.

    \(f(x)\), une fonction de probabilité continue, est égale à\(\frac{1}{3}\) et la fonction est limitée à\(1 \leq x \leq 4\). Décrivez\(P(x>\frac{3}{2})\).

    5.2 La distribution uniforme

    Utilisez les informations suivantes pour répondre aux dix prochaines questions. Les données qui suivent sont la superficie en pieds carrés (en 1 000 pieds carrés) de 28 maisons.

    \ (\ PageIndex {2} \) « >
    1,5 2.4 3.6 2.6 1,6 2.4 2,0
    3.5 2,5 1,8 2.4 2,5 3.5 4,0
    2.6 1,6 2.2 1,8 3.8 2,5 1,5
    2,8 1,8 4,5 1,9 1,9 3.1 1,6
    Tableau\(\PageIndex{2}\)

    La moyenne de l'échantillon = 2,50 et l'écart type de l'échantillon = 0,8302.

    La distribution peut être écrite sous la forme\(X \sim U(1.5, 4.5)\).

    16.

    De quel type de distribution s'agit-il ?

    17.

    Dans cette distribution, les résultats sont tout aussi probables. Qu'est-ce que cela signifie ?

    18.

    Quelle est la hauteur de\(f(x)\) la distribution de probabilité continue ?

    19.

    Quelles sont les contraintes qui pèsent sur les valeurs de\(x\) ?

    20.

    Graphe\(P(2 < x < 3)\).

    21.

    Qu'\(P(2 < x < 3)\)est-ce que c'est

    22.

    Qu'\(P(x < 3.5 | x < 4)\)est-ce que c'est

    23.

    Qu'\(P(x = 1.5)\)est-ce que c'est

    24.

    Déterminez la probabilité qu'une maison sélectionnée au hasard possède plus de 3 000 pieds carrés étant donné que vous savez déjà que la maison a plus de 2 000 pieds carrés.

    Utilisez les informations suivantes pour répondre aux huit exercices suivants. Une distribution est donnée sous la forme\(X \sim U(0, 12)\).

    25.

    Qu'\(a\)est-ce que c'est Qu'est-ce que cela représente ?

    26.

    Qu'\(b\)est-ce que c'est Qu'est-ce que cela représente ?

    27.

    Qu'est-ce que la fonction de densité de probabilité ?

    28.

    Quelle est la moyenne théorique ?

    29.

    Qu'est-ce que l'écart type théorique ?

    30.

    Dessinez le graphique de la distribution pour\(P(x > 9)\).

    31.

    Trouve\(P(x > 9)\).

    Utilisez les informations suivantes pour répondre aux onze exercices suivants. L'âge des voitures sur le parking du personnel d'un collège de banlieue est uniformément réparti entre six mois (0,5 an) et 9,5 ans.

    32.

    Qu'est-ce qui est mesuré ici ?

    33.

    Définissez la variable aléatoire en quelques mots\(X\).

    34.

    Les données sont-elles discrètes ou continues ?

    35.

    L'intervalle de valeurs pour\(x\) est ______.

    36.

    La distribution pour\(X\) est ______.

    37.

    Ecrivez la fonction de densité de probabilité.

    38.

    Tracez la distribution de probabilité.

    1. Esquissez le graphique de la distribution de probabilité.
      Il s'agit d'un modèle de graphique vierge. Les axes vertical et horizontal ne sont pas étiquetés.

      Figurine\(\PageIndex{31}\)

    2. Identifiez les valeurs suivantes :
      • Valeur la plus basse pour\(\overline{x}\) : _______
      • Valeur la plus élevée pour\(\overline{x}\) : _______
      • Hauteur du rectangle : _______
      • Étiquette pour l'axe X (mots) : _______
      • Étiquette pour l'axe Y (mots) : _______

    39.

    Déterminez l'âge moyen des voitures du lot.

    40.

    Déterminez la probabilité qu'une voiture choisie au hasard dans le lot ait moins de quatre ans.

    1. Esquissez le graphique et ombrez la zone d'intérêt.
      Graphe vide avec axes verticaux et horizontaux.

      Figurine\(\PageIndex{32}\)

    2. Déterminez la probabilité. \(P(x < 4)\)= _______

    41.

    En ne considérant que les voitures âgées de moins de 7,5 ans, déterminez la probabilité qu'une voiture choisie au hasard dans le lot ait moins de quatre ans.

    1. Esquissez le graphique, ombrez la zone d'intérêt.
      Il s'agit d'un modèle de graphique vierge. Les axes vertical et horizontal ne sont pas étiquetés.

      Figurine\(\PageIndex{33}\)

    2. Déterminez la probabilité. \(P(x < 4 | x < 7.5) =\)_______

    42.

    Qu'est-ce qui a changé dans les deux problèmes précédents qui a rendu les solutions différentes ?

    43.

    Déterminez le troisième quartile d'âge des voitures dans le lot. Cela signifie que vous devrez trouver la valeur de telle sorte que\(\frac{3}{4}\), soit 75 %, des voitures aient au plus cet âge (inférieur ou égal).

    1. Esquissez le graphique et ombrez la zone d'intérêt.
      Graphe vide avec axes verticaux et horizontaux.

      Figurine\(\PageIndex{34}\)

    2. Trouvez la valeur\(k\) telle que\(P(x < k) = 0.75\).
    3. Le troisième quartile est _______

    5.3 La distribution exponentielle

    Utilisez les informations suivantes pour répondre aux dix exercices suivants. Un représentant du service client doit passer un temps différent avec chaque client pour résoudre divers problèmes. Le temps passé avec chaque client peut être modélisé selon la répartition suivante :\(X \sim Exp(0.2)\)

    44.

    De quel type de distribution s'agit-il ?

    45.

    Les résultats sont-ils également probables dans cette distribution ? Pourquoi ou pourquoi pas ?

    46.

    Qu'\(m\)est-ce que c'est Qu'est-ce que cela représente ?

    47.

    Quel est le moyen ?

    48.

    Qu'est-ce que l'écart type ?

    49.

    Indiquez la fonction de densité de probabilité.

    50.

    Tracez la distribution.

    51.

    Trouve\(P(2 < x < 10)\).

    52.

    Trouve\(P(x > 6)\).

    53.

    Détermine le 70 e percentile.

    Utilisez les informations suivantes pour répondre aux sept exercices suivants. Une distribution est donnée sous la forme\(X \sim Exp(0.75)\).

    54.

    Qu'est-ce que moi ?

    55.

    Qu'est-ce que la fonction de densité de probabilité ?

    56.

    Qu'est-ce que la fonction de distribution cumulée ?

    57.

    Dessinez la distribution.

    58.

    Trouve\(P(x < 4)\).

    59.

    Détermine le 30 e percentile.

    60.

    Trouvez la médiane.

    61.

    Lequel est le plus grand, la moyenne ou la médiane ?

    Utilisez les informations suivantes pour répondre aux 16 exercices suivants. Le carbone 14 est un élément radioactif dont la demi-vie est d'environ 5 730 ans. On dit que le carbone 14 se dégrade de façon exponentielle. Le taux de décroissance est de 0,000121. Nous commençons avec un gramme de carbone 14. Nous nous intéressons au temps (années) qu'il faut pour décomposer le carbone 14.

    62.

    Qu'est-ce qui est mesuré ici ?

    63.

    Les données sont-elles discrètes ou continues ?

    64.

    Définissez la variable aléatoire en quelques mots\(X\).

    65.

    Qu'est-ce que le taux de décroissance (\(m\)) ?

    66.

    La distribution pour\(X\) est ______.

    67.

    Déterminez la quantité (pourcentage d'un gramme) de carbone 14 qui dure moins de 5 730 ans. Cela signifie, trouver\(P(x < 5,730)\).

    1. Esquissez le graphique et ombrez la zone d'intérêt.
      Il s'agit d'un modèle de graphique vierge. Les axes vertical et horizontal ne sont pas étiquetés.

      Figurine\(\PageIndex{35}\)

    2. Déterminez la probabilité. \(P(x < 5,730) =\)__________

    68.

    Déterminez le pourcentage de carbone 14 qui dure plus de 10 000 ans.

    1. Esquissez le graphique et ombrez la zone d'intérêt.
      Graphe vide avec axes horizontaux et verticaux.

      Figurine\(\PageIndex{36}\)

    2. Déterminez la probabilité. \(P(x > 10,000) =\)________

    69.

    Trente pour cent (30 %) du carbone 14 se décomposera d'ici combien d'années ?

    1. Esquissez le graphique et ombrez la zone d'intérêt.
      Il s'agit d'un modèle de graphique vierge. Les axes vertical et horizontal ne sont pas étiquetés.

      Figurine\(\PageIndex{37}\)

      Trouvez la valeur\(k\) telle que\(P(x < k) = 0.30\).