12.4 : Le produit Cross

Objectifs d'apprentissage

• Calculez le produit croisé de deux vecteurs donnés.
• Utilisez des déterminants pour calculer un produit croisé.
• Trouve un vecteur orthogonal à deux vecteurs donnés.
• Déterminez les surfaces et les volumes à l'aide du produit croisé.
• Calculez le couple d'un vecteur de force et de position donné.

Imaginez un mécanicien qui tourne une clé pour serrer un boulon. Le mécanicien applique une force à l'extrémité de la clé. Cela crée une rotation, ou un couple, qui resserre le boulon. Nous pouvons utiliser des vecteurs pour représenter la force appliquée par le mécanicien et la distance (rayon) entre le boulon et l'extrémité de la clé. Ensuite, nous pouvons représenter le couple par un vecteur orienté le long de l'axe de rotation. Notez que le vecteur de couple est orthogonal à la fois au vecteur de force et au vecteur de rayon.

Dans cette section, nous développons une opération appelée produit croisé, qui nous permet de trouver un vecteur orthogonal à deux vecteurs donnés. Le calcul du couple est une application importante des produits croisés, et nous examinerons le couple plus en détail plus loin dans la section.

Le produit croisé et ses propriétés

Le produit scalaire est une multiplication de deux vecteurs qui donne un scalaire. Dans cette section, nous présentons un produit de deux vecteurs qui génère un troisième vecteur orthogonal aux deux premiers. Réfléchissez à la façon dont nous pourrions trouver un tel vecteur. \(\vecs v=⟨v_1,v_2,v_3⟩\)Soit\(\vecs u=⟨u_1,u_2,u_3⟩\) des vecteurs non nuls. Nous voulons trouver un vecteur\(\vecs w=⟨w_1,w_2,w_3⟩\) orthogonal aux deux\(\vecs u\) et, c'\(\vecs v\)est-à-dire, nous voulons trouver un vecteur\(\vecs w\) tel que\(\vecs u ⋅ \vecs w=0\) et\( \vecs v⋅ \vecs w=0\). Par conséquent\(w_1\),\(w_2,\) et\(w_3\) doit satisfaire

\[u_1w_1+u_2w_2+u_3w_3=0 \label{eq1} \]

\[v_1w_1+v_2w_2+v_3w_3=0. \label{eq2} \]

Si nous multiplions l'équation du haut par\(v_3\) et l'équation du bas par\(u_3\) et que nous soustrayons, nous pouvons éliminer la variable\(w_3\), qui donne

\[(u_1v_3−v_1u_3)w_1+(u_2v_3−v_2u_3)w_2=0. \nonumber \]

Si nous sélectionnons

\[\begin{align*} w_1 &=u_2v_3−u_3v_2 \\[4pt] w_2 &=−(u_1v_3−u_3v_1), \end{align*}\]

nous obtenons un vecteur de solution possible. La substitution de ces valeurs dans les équations d'origine (équations \ ref {eq1} et \ ref {eq2}) donne

\[w_3=u_1v_2−u_2v_1. \nonumber \]

C'est-à-dire un vecteur

\[\vecs w=⟨u_2v_3−u_3v_2,−(u_1v_3−u_3v_1),u_1v_2−u_2v_1⟩ \nonumber \]

est orthogonal aux deux\(\vecs u\) et\(\vecs v\), ce qui nous amène à définir l'opération suivante, appelée produit croisé.

Définition : Cross Product

\(\vecs u=⟨u_1,u_2,u_3⟩\)Let and\(\vecs v=⟨v_1,v_2,v_3⟩.\) Then, le produit croisé\(\vecs u×\vecs v\) est un vecteur

\[\begin{align} \vecs u×\vecs v &= (u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1) \mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k} \nonumber \\[4pt] &=⟨u_2v_3−u_3v_2,−(u_1v_3−u_3v_1),u_1v_2−u_2v_1⟩. \label{cross}\end{align} \]

D'après la façon dont nous avons développé\(\vecs u×\vecs v\), il devrait être clair que le produit croisé est orthogonal à la fois à\(\vecs u\) et\(\vecs v\). Cependant, cela ne fait jamais de mal de vérifier. Pour montrer que\(\vecs u×\vecs v\) c'est orthogonal à\(\vecs u\), nous calculons le produit scalaire de\(\vecs u\) et\(\vecs u×\vecs v\).

\ [\ begin {align*} \ vecs u⋅ (\ vecs u× \ vecs v) &=rq_u_1, u_2, u_3·⋅rq−u_2v_3−u_3v_2, −u_1v_3+u_3v_1, u_1v_2−u_2v_1⟩ \ \ [4pt] &=u_1 (u_2v_1⟩ \ \ [4pt] &=u_1 (u_2v_1⟩ \ \ [4pt] _3−u_3v_2) +u_2 (−u_1v_3+u_3v_1) +u_3 (u_1v_2−u_2v_1) \ \ [4 points]
&=u_1u_2v_3−u_1u_3v_2−u_2−u_3v_3+u_2u_3v_1+u_1u_3v_2−u_3v_1+u_1u_3v_2−u_3v_1 _2−u_2u_3v_1 \ \ [4 points]
& =( u_1u_2v_3−u_1u_2) v_3) + (−u_1u_3v_2+u_1u_3v_2) + (u_2u_3v_1−u_2u_3v_1) \ \ [4 points]
&= 0 \ end {align*} \]

De la même manière, nous pouvons montrer que le produit croisé est également orthogonal à\(\vecs v\).

Le produit croisé\(\vecs{a}×\vecs{b}\) (vertical, en rose) change à mesure que l'angle entre les vecteurs\(\vecs{a}\) (bleu) et\(\vecs{b}\) (rouge) change. Le produit croisé (violet) est toujours perpendiculaire aux deux vecteurs et a une magnitude nulle lorsque les vecteurs sont parallèles et une magnitude maximale\(‖\vecs{a}‖‖\vecs{b}‖\) lorsqu'ils sont perpendiculaires. (Domaine public ; LucasVB).

Exemple\(\PageIndex{1}\): Finding a Cross Product

Laissons\(\vecs p=⟨−1,2,5⟩\) et\(\vecs q=⟨4,0,−3⟩\) (Figure\(\PageIndex{1}\)). Trouve\(\vecs p×\vecs q\).

 ». Le second vecteur est étiqueté « q = <4, 0, -3> »." src="https://math.libretexts.org/@api/dek...6870027545.png">

Figure\(\PageIndex{1}\) : Trouver un produit croisé pour deux vecteurs donnés.

Solution

Substituez les composantes des vecteurs dans l'équation \ ref {cross} :

\[\begin{align*} \vecs p×\vecs q &=⟨−1,2,5⟩×⟨4,0,−3⟩ \\[4pt] &= ⟨p_2q_3−p_3q_2,-(p_1q_3−p_3q_1),p_1q_2−p_2q_1⟩ \\[4pt] &= ⟨2(−3)−5(0),−(−1)(−3)+5(4),(−1)(0)−2(4)⟩ \\[4pt] &= ⟨−6,17,−8⟩.\end{align*}\]

Exercice\(\PageIndex{1}\)

\(\vecs p×\vecs q\)Recherchez\(\vecs p=⟨5,1,2⟩\) et\(\vecs q=⟨−2,0,1⟩.\) exprimez la réponse à l'aide de vecteurs unitaires standard.

Allusion

Utilisez la formule\(\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k}.\)

Réponse

\(\vecs p×\vecs q = \mathbf{\hat i}−9\mathbf{\hat j}+2\mathbf{\hat k}\)

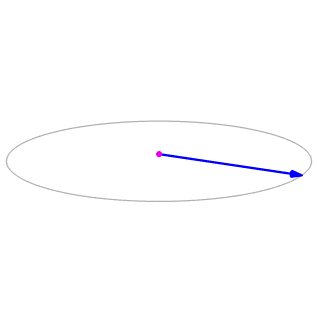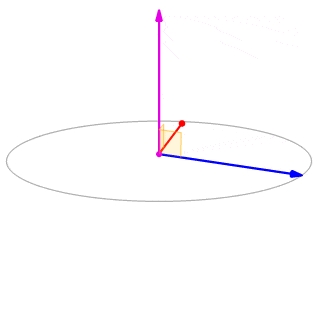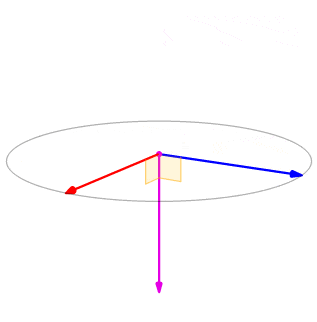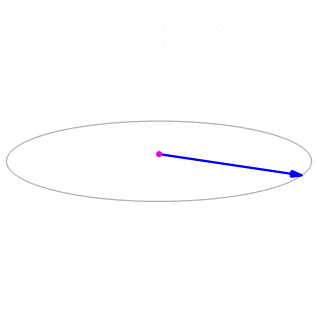
Bien que cela ne soit pas évident à partir de l'équation \ ref {cross}, la direction de\(\vecs u×\vecs v\) est donnée par la règle de droite. Si nous tenons la main droite avec les doigts pointés dans la direction de\(\vecs u\), puis que nous courbons les doigts vers le vecteur\(\vecs v\), le pouce pointe dans la direction du produit croisé, comme indiqué sur la figure\(\PageIndex{2}\).

Figure\(\PageIndex{2}\) : La direction de\( \vecs u× \vecs v\) est déterminée par la règle de la main droite.

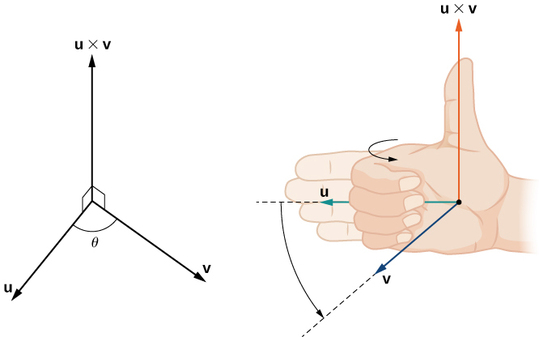
Remarquez ce que cela signifie pour la direction de\(\vecs v×\vecs u\). Si nous appliquons la règle de la main droite à\(\vecs v×\vecs u\), nous commençons avec nos doigts pointés dans la direction de\(\vecs v\), puis nous courbons nos doigts vers le vecteur\(\vecs u\). Dans ce cas, le pouce pointe dans la direction opposée à\(\vecs u×\vecs v\). (Essayez-le !)

Exemple\(\PageIndex{2}\): Anticommutativity of the Cross Product

Laissez\(\vecs u=⟨0,2,1⟩\) et\(\vecs v=⟨3,−1,0⟩\). \(\vecs u×\vecs v\)Calculez-les\(\vecs v×\vecs u\) et graphiez-les.

 ». Le second vecteur est étiqueté « v = <3, -1, 0> »." src="https://math.libretexts.org/@api/dek...9414463549.png">

Figure\(\PageIndex{3}\) : Les produits croisés sont-ils\(\vecs u×\vecs v\) orientés\(\vecs v×\vecs u\) dans le même sens ?

Solution

Nous avons

\(\vecs u×\vecs v=⟨(0+1),−(0−3),(0−6)⟩=⟨1,3,−6⟩\)

\(\vecs v×\vecs u=⟨(−1−0),−(3−0),(6−0)⟩=⟨−1,−3,6⟩.\)

Nous le voyons, dans ce cas,\(\vecs u×\vecs v=−(\vecs v×\vecs u)\) (Figure\(\PageIndex{4}\)). Nous le prouvons en général plus loin dans cette section.

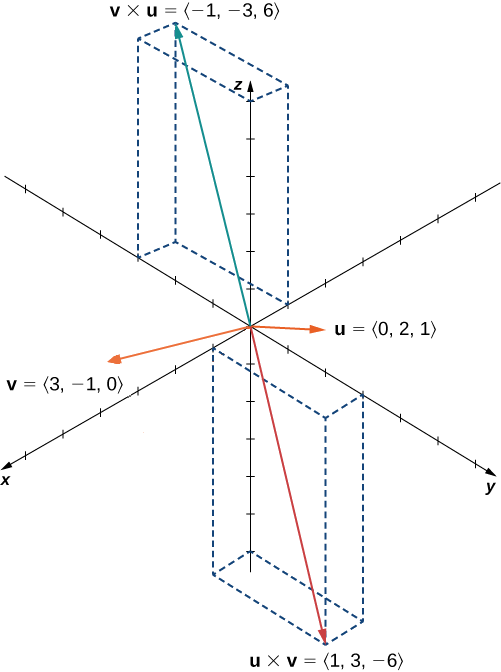
Figure\(\PageIndex{4}\) : Les produits croisés\(\vecs{u}×\vecs{v}\) et\(\vecs{v}×\vecs{u}\) sont tous deux orthogonaux à\(\vecs{u}\) et\(\vecs{v}\), mais dans des directions opposées.

Exercice\(\PageIndex{2}\)

Supposons que\(\vecs u\) des vecteurs\(\vecs v\) se trouvent dans le\(xy\) plan\(z\) -plane (la composante -de chaque vecteur est zéro). Supposons maintenant que les\(y\) composantes\(x\) - et -de\(\vecs u\) et la\(y\) composante -de\(\vecs v\) sont toutes positives, alors que la\(x\) composante -de\(\vecs v\) est négative. En supposant que les axes de coordonnées sont orientés dans les positions habituelles, dans quelle direction\(\vecs u×\vecs v\) pointent-ils ?

Allusion

N'oubliez pas la règle de la main droite (Figure\(\PageIndex{2}\)).

Réponse

Vers le haut (\(z\)direction positive)

Les produits croisés des vecteurs unitaires standard\(\mathbf{\hat i}\)\(\mathbf{\hat j}\), et\(\mathbf{\hat k}\) peuvent être utiles pour simplifier certains calculs. Examinons donc ces produits croisés. Une simple application de la définition montre que

\[\mathbf{\hat i}×\mathbf{\hat i}=\mathbf{\hat j}×\mathbf{\hat j}=\mathbf{\hat k}×\mathbf{\hat k}=\vecs 0. \nonumber \]

(Le produit croisé de deux vecteurs est un vecteur, donc chacun de ces produits donne le vecteur zéro, et non le scalaire\(0\).) C'est à vous de vérifier vous-même les calculs.

De plus, comme le produit croisé de deux vecteurs est orthogonal à chacun de ces vecteurs, nous savons que le produit croisé de\(\mathbf{\hat i}\) et\(\mathbf{\hat j}\) est parallèle à\(\mathbf{\hat k}\). De même, le produit vectoriel de\(\mathbf{\hat i}\) et\(\mathbf{\hat k}\) est parallèle à\(\mathbf{\hat j}\), et le produit vectoriel de\(\mathbf{\hat j}\) et\(\mathbf{\hat k}\) est parallèle à\(\mathbf{\hat i}\).

Nous pouvons utiliser la règle de la main droite pour déterminer la direction de chaque produit. Ensuite, nous avons

\ [\ begin {align*} \ mathbf {\ hat i} × \ mathbf {\ hat j} &= \ mathbf {\ hat k} \ \ [4pt]
 \ mathbf {\ hat j} × \ mathbf {\ hat i} &=− \ mathbf {\ hat k} \ \ [10 points]
 \ mathbf {\ hat j} × \ mathbf {\ hat k} &= \ mathbf {\ hat i} \ \ [4pt]
 \ mathbf {\ hat k} × \ mathbf {\ hat j} &=− \ mathbf {\ hat i} \ \ [10 pt]
 \ mathbf {\ hat k} × \ mathbf {\ hat i} &= \ mathbf {\ hat j} \ \ [4 points]
 \ mathbf {\ hat i} × \ mathbf {\ hat k} &=− \ mathbf {\ hat j}. \ end {align*} \]

Ces formules seront utiles plus tard.

Exemple\(\PageIndex{3}\): Cross Product of Standard Unit Vectors

Trouve\(\mathbf{\hat i} ×(\mathbf{\hat j}×\mathbf{\hat k})\).

Solution

Nous le savons\(\mathbf{\hat j}×\mathbf{\hat k}=\mathbf{\hat i}\). Par conséquent,\(\mathbf{\hat i}×(\mathbf{\hat j}×\mathbf{\hat k})=\mathbf{\hat i}×\mathbf{\hat i}=\vecs 0.\)

Exercice\(\PageIndex{3}\)

Trouvez\((\mathbf{\hat i}×\mathbf{\hat j})×(\mathbf{\hat k}×\mathbf{\hat i}).\)

Allusion

N'oubliez pas la règle de la main droite (Figure\(\PageIndex{2}\)).

Réponse

\(−\mathbf{\hat i}\)

Comme nous l'avons vu, le produit scalaire est souvent appelé produit scalaire car il donne un scalaire. Le produit croisé donne un vecteur, c'est pourquoi il est parfois appelé produit vectoriel. Ces opérations sont toutes deux des versions de la multiplication vectorielle, mais elles ont des propriétés et des applications très différentes. Explorons certaines propriétés du produit croisé. Nous n'en prouvons que quelques-unes. Les preuves des autres propriétés sont laissées sous forme d'exercices.

Propriétés du produit croisé

\(\vecs w\)Soyons\(\vecs u,\vecs v,\) des vecteurs dans l'espace, et\(c\) soyons un scalaire.

1. Propriété anticommutative :\[\vecs u×\vecs v=−(\vecs v×\vecs u) \nonumber \]
2. Propriété distributive :\[\vecs u×(\vecs v+\vecs w)=\vecs u×\vecs v+\vecs u×\vecs w \nonumber \]
3. Multiplication par une constante :\[c(\vecs u×\vecs v)=(c\vecs u)×\vecs v=\vecs u×(c\vecs v) \nonumber \]
4. Produit croisé du vecteur zéro :\[\vecs u×\vecs 0=\vecs 0×\vecs u=\vecs 0 \nonumber \]
5. Produit croisé d'un vecteur avec lui-même :\[\vecs v×\vecs v=\vecs 0 \nonumber \]
6. Produit triple scalaire :\[\vecs u⋅(\vecs v×\vecs w)=(\vecs u×\vecs v)⋅\vecs w \nonumber \]

Une preuve

Pour la propriété\(i\), nous voulons montrer que\(\vecs u×\vecs v=−(\vecs v×\vecs u).\) nous avons

\[\begin{align*} \vecs u×\vecs v &=⟨u_1,u_2,u_3⟩×⟨v_1,v_2,v_3⟩ \\[4pt] &=⟨u_2v_3−u_3v_2,−u_1v_3+u_3v_1,u_1v_2−u_2v_1⟩ \\[4pt] &=−⟨u_3v_2−u_2v_3,−u_3v_1+u_1v_3,u_2v_1−u_1v_2⟩ \\[4pt] &=−⟨v_1,v_2,v_3⟩×⟨u_1,u_2,u_3⟩\\[4pt] &=−(\vecs v×\vecs u).\end{align*}\]

Contrairement à la plupart des opérations que nous avons vues, le produit croisé n'est pas commutatif. Cela a du sens si l'on pense à la règle de la main droite.

Pour la propriété\(iv\), cela découle directement de la définition du produit croisé. Nous avons

\[\vecs u × \vecs 0=⟨u_2(0)−u_3(0),−(u_1(0)−u_3(0)),u_1(0)−u_2(0)⟩=⟨0,0,0⟩=\vecs 0. \nonumber \]

Ensuite, par propriété i.,\(\vecs 0×\vecs u=\vecs 0\) également. N'oubliez pas que le produit scalaire d'un vecteur et du vecteur zéro est le scalaire\(0\), alors que le produit croisé d'un vecteur avec le vecteur zéro est le vecteur\(\vecs 0\).

Propriété\(vi\). ressemble à la propriété associative, mais notez la modification des opérations :

\ [\ begin {align*} \ vecs u⋅ (\ vecs v× \ vecs w) &=u⋅105/v_2w_3−v_3w_2, −v_1w_3+v_3w_1, v_1w_2−v_2w_1⟩ \ \ [4 points]
&= u_1 (v_2w_3−v_3w_2) +u_1 _2 (−v_1w_3+v_3w_1) +u_3 (v_1w_2−v_2w_1) \ \ [4 points]
&=u_1v_2w_3−u_1v_3w_3−u_2−u_2v_1w_3+u_2v_3w_1+u_3v_1w_2−u_3v_2w_2_w_1 \ \ [4 points]
et =( u_2v_3−u_3v) _2) w_1+ (u_3v_1−u_1v_3) w_2+ (u_1v_2−u_2v_1) w_3 \ \ [4 points]
&=u_2v_3−u_3v_2, u_3v_1−u_1v_3, u_1v_2−u_2−u_2v_1−u_3−u_3v_2, w_1 3⟩ =( \ vecs u× \ vecs v) ⋅ \ vecs w. \ end {align*} \]

\(\square\)

Exemple\(\PageIndex{4}\): Using the Properties of the Cross Product

Utilisez les propriétés croisées des produits pour calculer\((2\mathbf{\hat i}×3\mathbf{\hat j})×\mathbf{\hat j}.\)

Solution

\ [\ begin {align*} (2 \ mathbf {\ hat i} ×3 \ mathbf {\ hat j}) × \ mathbf {\ hat j} &=2 (\ mathbf {\ hat i} ×3 \ mathbf {\ hat j}) × \ mathbf {\ hat j} \ \ [4pt] &=2 (3) (\ mathbf {\ hat j} \ [4pt]
&=2 (3) (\ mathbf {\ hat j} hat i} × \ mathbf {\ hat j}) × \ mathbf {\ hat j} \ \ [4 points]
& =( 6 \ mathbf {\ hat k}) × \ mathbf {\ hat j} \ \ [4 points]
&=6 (\ mathbf { \ hat k} × \ mathbf {\ hat j}) \ \ [4pt]
&=6 (− \ mathbf {\ hat i}) =−6 \ mathbf {\ hat i}. \ end {align*} \]

Exercice\(\PageIndex{4}\)

Utilisez les propriétés du produit croisé pour calculer\((\mathbf{\hat i}×\mathbf{\hat k})×(\mathbf{\hat k}×\mathbf{\hat j}).\)

Allusion

\(\vecs u×\vecs v=−(\vecs v×\vecs u)\)

Réponse

\(−\mathbf{\hat k}\)

Jusqu'à présent, dans cette section, nous nous sommes intéressés à la direction du vecteur\(\vecs u×\vecs v\), mais nous n'avons pas discuté de sa magnitude. Il s'avère qu'il existe une expression simple pour désigner l'ampleur de l'\(\vecs u×\vecs v\)implication des magnitudes de\(\vecs u\) et\(\vecs v\) et du sinus de l'angle qui les sépare.

Ampleur du produit croisé

Soyons\(\vecs u\)\(\vecs v\) des vecteurs, et\(θ\) que ce soit l'angle entre eux. Ensuite,\(‖\vecs u×\vecs v‖=‖\vecs u‖⋅‖\vecs v‖⋅\sin θ.\)

Une preuve

\(\vecs v=⟨v_1,v_2,v_3⟩\)Soit\(\vecs u=⟨u_1,u_2,u_3⟩\) des vecteurs, et\(θ\) notons l'angle qui les sépare. Alors

\ [\ begin {align*} « \ vecs u× \ vecs v^2 &= (u_2v_3−u_3v_2) ^2+ (u_3v_1−u_1v_3) ^2+ (u_1v_2−u_2v_1) ^2 \ \ [4 points]
&=u^2_2_2v^2_3−2u_2_u_2_u_u_2_u_u_2_u_u_u_2_u_u_u_u_2_u_u_u_2_u_u_3v_2v_3+u^2_3v^2_2+u^2_3v^2_1−2u_1u_3v_1v_3+u^2_1v^2_3+u^2_1v^2_2−2u_1u_2v_1v_2+u^2_2v^2_2_2_2_2_1 \ \ [4 points] &=u2^2_2_v^2_2_1 \ [4 points]
&=u2_1v_1v_2_1 \ \ [4 points] &=u2^v^2_1+u^2_1v^2_2+u^2_1v^2_3+u^2_2_2_1+u^2_2_2_2v ^2_2+u^2_2v^2_3+u^2_3v^2_1+u^2_3v^2_2+u^2_3v^2_3− (u^2_1v^2_2_2_v^2_2_2+u^2_3v^2_3+2u_1u_2v_1v_2+2u_1v_2+2u_1v_2+2u_1v_2+2u_1v_2+2u_1v_2+2u_1v_2+2u_1v_2+u_3v_1v_3+2u_2u_3v_2v_3) \ \ [4 points]
et =( u^2_1+u^2_2+u^2_2+u^2_3) (v^2_1+v^2_3) − (u_1v_1+u_2v_2+u_3v_3) ^2 \ \ [4pt]
&=⟩ \ vecs u^2 \ vecs v^2− (\ vecs u⋅ \ vecs v) ^2 \ \ [4 points]
&=⟩ \ vecs u^2 \ vecs v^2−− \ vecs u^2 \ vecs v^2 \ cos^2θ \ \ [4 points]
&=\ vecs u^2 \ vecs v^2 (1− \ cos^2θ) \ \ [4 points]
&=) \ \ vecs u^2 \ vecs v^2 ^2 (\ sin^2θ). \ end {align*} \ nonumber \]

En prenant des racines carrées et en constatant que\(\sqrt{\sin^2θ}=\sinθ\)\(0≤θ≤180°,\) nous avons le résultat souhaité :

\[‖\vecs u×\vecs v‖=‖\vecs u‖‖\vecs v‖ \sin θ. \nonumber \]

□

Cette définition du produit croisé nous permet de visualiser ou d'interpréter le produit de manière géométrique. Il est clair, par exemple, que le produit croisé n'est défini que pour les vecteurs en trois dimensions, et non pour les vecteurs en deux dimensions. En deux dimensions, il est impossible de générer un vecteur simultanément orthogonal à deux vecteurs non parallèles.

Exemple\(\PageIndex{5}\): Calculating the Cross Product

Utilisez « Magnitude du produit croisé » pour déterminer l'amplitude du produit croisé de\(\vecs u=⟨0,4,0⟩\) et\(\vecs v=⟨0,0,−3⟩\).

Solution

Nous avons

\ [\ begin {align*} ⟩ \ vecs u× \ vecs v^= {\ vecs u⋅ \ vecs v⋅ \ sinθ \ \ [4 points]
&= \ sqrt {0^2+4^2+0^2} ⋅ \ sqrt {0^2+0^2+ (−3) ^2} ⋅ \ sin {\ dfrac {π} {2}} \ \ [4 points]
&=4 (3) (1) =12 \ end {align*} \]

Exercice\(\PageIndex{5}\)

Utilisez « Magnitude du produit croisé » pour déterminer l'amplitude de\(\vecs u×\vecs v\), où\(\vecs u=⟨−8,0,0⟩\) et\(\vecs v=⟨0,2,0⟩\).

Allusion

Les vecteurs\(\vecs u\) et\(\vecs v\) sont orthogonaux.

Réponse

16

Déterminants et produit croisé

L'utilisation de l'équation \ ref {cross} pour trouver le produit croisé de deux vecteurs est simple, et elle présente le produit croisé sous la forme d'un composant utile. La formule est toutefois complexe et difficile à retenir. Heureusement, nous avons une alternative. Nous pouvons calculer le produit croisé de deux vecteurs en utilisant la notation déterminante.

Un\(2×2\) déterminant est défini par

\[\begin{vmatrix}a_1 & b_1\\a_2 & b_2\end{vmatrix} =a_1b_2−b_1a_2. \nonumber \]

Par exemple,

\[\begin{vmatrix}3 & −2\\5 & 1\end{vmatrix} =3(1)−5(−2)=3+10=13. \nonumber \]

Un\(3×3\) déterminant est défini en termes de\(2×2\) déterminants comme suit :

\[\begin{vmatrix}a_1 & a_2 & a_3\\b_1 & b_2 & b_3\\c_1 & c_2 & c_3\end{vmatrix}=a_1\begin{vmatrix}b_2 & b_3\\c_2 & c_3\end{vmatrix}−a_2\begin{vmatrix}b_1 & b_3\\c_1 & c_3\end{vmatrix}+a_3\begin{vmatrix}b_1 & b_2\\c_1 & c_2\end{vmatrix}.\label{expandEqn} \]

L'équation \ ref {ExpandeQn} est appelée expansion du déterminant le long de la première ligne. Notez que les multiplicateurs de chacun des\(2×2\) déterminants sur le côté droit de cette expression sont les entrées de la première ligne du\(3×3\) déterminant. En outre, chacun des\(2×2\) déterminants contient les entrées du\(3×3\) déterminant qui resteraient si vous barriez la ligne et la colonne contenant le multiplicateur. Ainsi, pour le premier terme à droite,\(a_1\) se trouve le multiplicateur, et le\(2×2\) déterminant contient les entrées qui restent si vous supprimez la première ligne et la première colonne du\(3×3\) déterminant. De même, pour le second terme, le multiplicateur est\(a_2\), et le\(2×2\) déterminant contient les entrées qui restent si vous barrez la première ligne et la deuxième colonne du\(3×3\) déterminant. Notez cependant que le coefficient du second terme est négatif. Le troisième terme peut être calculé de la même manière.

Exemple\(\PageIndex{6}\): Using Expansion Along the First Row to Compute a \(3×3\) Determinant

Évaluez le déterminant\(\begin{vmatrix}2 & 5 &−1\\−1 & 1 & 3\\−2 & 3 & 4\end{vmatrix}\).

Solution

Nous avons

\ [\ begin {align*} \ begin {vmatrix} 2 et 5 et −1 \ \ −1 et 1 et 3 \ \ −2 et 3 et 4 \ end {vmatrix} &=2 \ begin {vmatrix} 1 et 3 \ \ 3 et 4 \ end {vmatrix} −5 \ begin {vmatrix} −1 et 3 \ \ −2 et 4 \ end {vmatrix} −1 \ begin {vmatrix} −1 \ begin {vmatrix} −5 \ begin {vmatrix} −1 \ begin {vmatrix} matrix} −1 et 1 \ \ −2 et 3 \ end {vmatrix} \ \ [4 points]
&=2 (4−9) −5 (−4+6) −1 (−3+2) ) \ \ [4 points]
&= 2 (−5) −5 (2) −1 (−1) =−10−10+1 \ \ [4 points]
&=−19 \ end {align*} \]

Exercice\(\PageIndex{6}\)

Évaluez le déterminant\(\begin{vmatrix}1 & −2 & −1\\3 & 2 & −3\\1 & 5 & 4\end{vmatrix}\).

Allusion

Développez le long de la première rangée. N'oubliez pas que le second terme est négatif !

Réponse

40

Techniquement, les déterminants sont définis uniquement en termes de tableaux de nombres réels. Cependant, la notation déterminante fournit un dispositif mnémotechnique utile pour la formule des produits croisés.

Règle : produit croisé calculé par un déterminant

Laissez\(\vecs u=⟨u_1,u_2,u_3⟩\) et\(\vecs v=⟨v_1,v_2,v_3⟩\) soyez des vecteurs. Ensuite, le produit croisé\(\vecs u×\vecs v\) est donné par

\[\vecs u×\vecs v=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\u_1 & u_2 & u_3\\v_1 & v_2 & v_3\end{vmatrix}=\begin{vmatrix}u_2 & u_3\\v_2 & v_3\end{vmatrix}\mathbf{\hat i}−\begin{vmatrix}u_1 & u_3\\v_1 & v_3\end{vmatrix}\mathbf{\hat j}+\begin{vmatrix}u_1 & u_2\\v_1 & v_2\end{vmatrix}\mathbf{\hat k}. \nonumber \]

Exemple\(\PageIndex{7}\): Using Determinant Notation to find \(\vecs p×\vecs q\)

Laissez\(\vecs p=⟨−1,2,5⟩\) et\(\vecs q=⟨4,0,−3⟩\). Trouve\(\vecs p×\vecs q\).

Solution

Nous définissons notre déterminant en plaçant les vecteurs unitaires standard sur la première ligne, les composantes de\(\vecs u\) la deuxième rangée et les composantes\(\vecs v\) de la troisième rangée. Ensuite, nous avons

\ [\ begin {align*} \ vecs p× \ vecs q &= \ begin {vmatrix} \ mathbf {\ hat i} & \ mathbf {\ hat j} & \ mathbf {\ hat k} \ \ -1 et 2 et 5 \ \ 4 et 0 et −3 \ end {vmatrix} = \ begin {vmatrix} 2 et 5 \ \ 0 et −3 \ {end vmatrix} \ mathbf {\ hat i} − \ begin {vmatrix} −1 et 5 \ \ 4 et −3 \ end {vmatrix} \ mathbf {\ hat j} + \ begin {vmatrix} − 1 et 2 \ \ 4 et 0 \ end {vmatrix} \ mathbf {\ hat k} \ \ [4 points]
&= (−6−0) \ mathbf {\ hat i} − (3−20) \ mathbf {\ hat j} + (0−8) \ mathbf {\ hat k} \ \ [4 points]
&=−6 \ mathbf {\ hat i} +17 \ mathbf {\ hat j} −8 \ mathbf {\ hat k}. \ end {align*} \]

Notez que cette réponse confirme le calcul du produit croisé dans Example\(\PageIndex{1}\).

Exercice\(\PageIndex{7}\)

Utilisez la notation déterminante pour trouver\(\vecs a×\vecs b\), où\(\vecs a=⟨8,2,3⟩\) et\(\vecs b=⟨−1,0,4⟩.\)

Allusion

Calculez le déterminant\(\begin{vmatrix}\mathbf{\hat i} \mathbf{\hat j} \mathbf{\hat k}\\8 & 2 & 3\\−1 & 0 & 4\end{vmatrix}\).

Réponse

\(\vecs a×\vecs b = 8\mathbf{\hat i}−35\mathbf{\hat j}+2\mathbf{\hat k}\)

Utilisation du produit Cross

Le produit croisé est très utile pour plusieurs types de calculs, y compris la recherche d'un vecteur orthogonal à deux vecteurs donnés, le calcul des zones de triangles et de parallélogrammes, et même la détermination du volume de la forme géométrique tridimensionnelle constituée de parallélogrammes appelés parallélépipèdes. Les exemples suivants illustrent ces calculs.

Exemple\(\PageIndex{8}\): Finding a Unit Vector Orthogonal to Two Given Vectors

Laissez\(\vecs a=⟨5,2,−1⟩\) et\(\vecs b=⟨0,−1,4⟩\). Trouvez un vecteur unitaire orthogonal à la fois à\(\vecs a\) et\(\vecs b\).

Solution

Le produit croisé\(\vecs a×\vecs b\) est orthogonal aux deux vecteurs\(\vecs a\) et\(\vecs b\). On peut le calculer avec un déterminant :

\ [\ begin {align*} \ vecs a× \ vecs b &= \ begin {vmatrix} \ mathbf {\ hat i} & \ mathbf {\ hat j} & \ mathbf {\ hat k} \ \ 5 et 2 & −1 \ \ 0 et −1 et −1 \ \ 0 et −1 \ \ 0 et −1 \ \ 0 et −1 \ \ 0 et −1 \ \ 0 et −1 \ \ 0 et −1 \ \ 0 et −1 \ \ 0 et −1 \ \ 0 & −1 et −1 \ \ 0 et −1 \ \ 0 et −1 \ {vmatrix} \ mathbf {\ hat i} − \ begin {vmatrix} 5 et −1 \ \ 0 et 4 \ end {vmatrix} \ mathbf {\ hat j} + \ begin {vmatrix} 5 & 2 \ \ 0 et −1 \ end {vmatrix} \ mathbf {\ hat k} \ \ [4 points]
& =( 8−1) \ mathbf {\ hat i} − (20−0) \ mathbf {\ hat j} + (−5−0) \ mathbf {\ hat k} \ \ [4 points]
&=7 \ mathbf {\ hat i} −20 \ mathbf {\ hat j} −5 \ mathbf {\ hat k}. \ end {align*} \ nonumber \]

Normalisez ce vecteur pour trouver un vecteur unitaire dans la même direction :

\(\|\vecs a×\vecs b\|=\sqrt{(7)^2+(−20)^2+(−5)^2}=\sqrt{474}\).

Ainsi,\(\left\langle\dfrac{7}{\sqrt{474}},\dfrac{−20}{\sqrt{474}},\dfrac{−5}{\sqrt{474}}\right\rangle\) est un vecteur unitaire orthogonal à\(\vecs a\) et\(\vecs b\).

Simplifié, ce vecteur devient\(\left\langle\dfrac{7\sqrt{474}}{474},\dfrac{−10\sqrt{474}}{237},\dfrac{−5\sqrt{474}}{474}\right\rangle\).

Exercice\(\PageIndex{8}\)

Trouvez un vecteur unitaire orthogonal à la fois à\(\vecs a\) et\(\vecs b\), où\(\vecs a=⟨4,0,3⟩\) et\(\vecs b=⟨1,1,4⟩.\)

Allusion

Normalisez le produit croisé.

Réponse

\(\left\langle\dfrac{−3}{\sqrt{194}},\dfrac{−13}{\sqrt{194}},\dfrac{4}{\sqrt{194}}\right\rangle\)ou, simplifié comme\(\left\langle\dfrac{−3\sqrt{194}}{194},\dfrac{−13\sqrt{194}}{194},\dfrac{2\sqrt{194}}{97}\right\rangle\)

Pour utiliser le produit croisé pour calculer les surfaces, nous énonçons et prouvons le théorème suivant.

Aire d'un parallélogramme

Si nous localisons des vecteurs\(\vecs u\) et\(\vecs v\) qu'ils forment les côtés adjacents d'un parallélogramme, alors l'aire du parallélogramme est donnée par\(‖\vecs u×\vecs v‖\) (Figure\(\PageIndex{5}\)).

Figure\(\PageIndex{5}\) : Le parallélogramme avec ses côtés\(\vecs u\) adjacents,\(\vecs v\) sa base\(‖\vecs u‖\) et sa hauteur\(‖\vecs v‖\sin θ\).

Une preuve

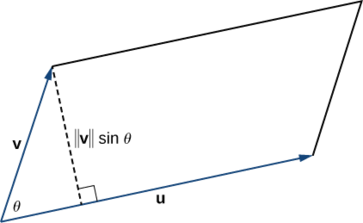
Nous montrons que l'amplitude du produit croisé est égale à la base multipliée par la hauteur du parallélogramme.

\[\begin{align*} \text{Area of a parallelogram} &= \text{base} × \text{height} \\[4pt] &=‖\vecs u‖(‖\vecs v‖\sin θ) \\[4pt] &=‖\vecs u×\vecs v‖ \end{align*}\]

□

Exemple\(\PageIndex{9}\): Finding the Area of a Triangle

\(R=(0,0,1)\)Soyons\(P=(1,0,0),Q=(0,1,0),\) les sommets d'un triangle (Figure\(\PageIndex{6}\)). Trouvez sa région.

Figure\(\PageIndex{6}\) : Déterminer l'aire d'un triangle à l'aide du produit croisé.

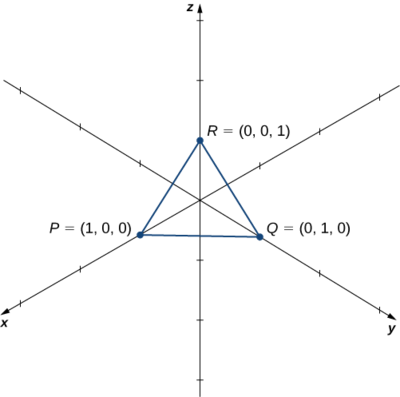
Solution

Nous avons\(\vecd{PQ}=⟨0−1,1−0,0−0⟩=⟨−1,1,0⟩\) et\(\vecd{PR}=⟨0−1,0−0,1−0⟩=⟨−1,0,1⟩\). L'aire du parallélogramme avec\(\vecd{PQ}\) les côtés adjacents\(\vecd{PR}\) est donnée par\(∥\vecd{PQ}×\vecd{PR}∥\) :

\ [\ begin {align*} \ vecd {PQ} \ times \ vecd {PR} &= \ begin {vmatrix} \ mathbf {\ hat i} & \ mathbf {\ hat j} & \ mathbf {\ hat k} \ \ −1 et 0 \ \ −1 et 0 \ \ −1 et 0 et 1 \ end {vmatrix} \ \ [4 points]
&= (1−0) \ mathbf {\ hat i} − (−1−0) \ mathbf {\ hat j} + (0− (−1)) \ mathbf {\ hat k} \ \ [4 points]
&= \ mathbf {\ hat i} + \ mathbf {\ hat j} + \ mathbf {\ hat k} \ \ [10 points]
 \ vecd {PQ} × \ vecd {PR} &=kcal 1,1,1\ \ [4 points]
&= \ sqrt {1^2+1^2+1^2} \ \ [4 points]
&= \ sqrt {3}. \ end {align*} \ nonumber \]

La surface de\(ΔPQR\) est égale à la moitié de la surface du parallélogramme ou\(\sqrt{3}/2 \, \text{units}^2\).

Exercice\(\PageIndex{9}\)

Trouvez l'aire du parallélogramme\( PQRS\) avec les sommets\( P(1,1,0)\)\(Q(7,1,0)\),\(R(9,4,2)\), et\( S(3,4,2)\).

Allusion

Esquissez le parallélogramme et identifiez deux vecteurs qui forment les côtés adjacents du parallélogramme.

Réponse

\(6\sqrt{13}\, \text{units}^2\)

Le produit Triple Scalar

Comme le produit croisé de deux vecteurs est un vecteur, il est possible de combiner le produit scalaire et le produit croisé. Le produit scalaire d'un vecteur avec le produit croisé de deux autres vecteurs est appelé produit scalaire triple car le résultat est un scalaire.

Définition : Produit triple scalaire

Le produit scalaire triple des vecteurs\( \vecs u\),\( \vecs v,\) et\(\vecs w\) est

\[ \vecs u⋅( \vecs v× \vecs w). \nonumber \]

Calcul d'un produit triple scalaire

Le produit scalaire triple des vecteurs

\[ \vecs u=u_1 \mathbf{\hat i}+u_2 \mathbf{\hat j}+u_3\mathbf{\hat k} \nonumber \]

\[ \vecs v=v_1\mathbf{\hat i}+v_2\mathbf{\hat j}+v_3\mathbf{\hat k} \nonumber \]

et

\[ \vecs w=w_1 \mathbf{\hat i}+w_2\mathbf{\hat j}+w_3\mathbf{\hat k} \nonumber \]

est le déterminant de la\(3×3\) matrice formée par les composantes des vecteurs :

\[ \vecs u⋅( \vecs v× \vecs w)=\begin{vmatrix}u_1 & u_2 & u_3\\v_1 & v_2 & v_3\\w_1 & w_2 & w_3\end{vmatrix}. \label{triple2} \]

Une preuve

Le calcul est simple.

\ [\ begin {align*} \ vecs u⋅ (\ vecs v× \ vecs w) &=rq_u_1, u_2, u_3·⋅⌘v_2w_3−v_3w_2, −v_1w_3+v_3w_1, v_1w_2−v_2w_1⟩ \ \ [4pt] &=u_1 (v_2w_1−v_2w_1⟩ \ \ [4pt] &=u_1 (v_2w_1) _3−v_3w_2) +u_2 (−v_1w_3+v_3w_1) +u_3 (v_1w_2−v_2w_1) \ \ [4 points]
&=u_1 (v_2w_3−v_3w_2) −u_2 (v_1w_3−v_3w_1) +u_3 (v_1w_3w_1) +u_3 (v_1w_3−v_3w_1) _2−v_2w_1) \ \ [4 points]
&= \ begin {vmatrix} u_ 1 & u_2 et u_3 \ \ v_1 et v_2 et v_3 \ \ w_1 et w_2 et w_3 \ end {vmatrix}. \ end {align*} \ nonumber \]

□

Exemple\(\PageIndex{10}\): Calculating the Triple Scalar Product

Laissez\(\vecs u=⟨1,3,5⟩,\,\vecs v=⟨2,−1,0⟩\) et\(\vecs w=⟨−3,0,−1⟩\). Calculez le produit scalaire triple\(\vecs u⋅(\vecs v×\vecs w).\)

Solution

Appliquez directement l'équation \ ref {triple2} :

\ [\ begin {align*} \ vecs u⋅ (\ vecs v× \ vecs w) &= \ begin {vmatrix} 1 et 3 et 5 \ \ 2 et −1 et 0 \ \ −3 & 0 et −1 \ end {vmatrix} \ \ [4pt]
&=1 \ begin {vmatrix} −1 et 0 \ \ 0 et −1 \ end {vmatrix} −3 \ begin {vmatrix} 2 et 0 \ \ −3 et −1 \ end {vmatrix} +5 \ begin {vmatrix} 2 et −1 \ \ −3 et 0 \ end { vmatrix} \ \ [4 points]
& =( 1−0) −3 (−2−0) +5 (0−3) \ \ [4 points]
&=1+6−15=−8. \ end {align*} \ nonumber \]

Exercice\(\PageIndex{10}\)

Calculez le produit scalaire triple\(\vecs a⋅(\vecs b×\vecs c),\) où\(\vecs a=⟨2,−4,1⟩, \vecs b=⟨0,3,−1⟩\), et\(\vecs c=⟨5,−3,3⟩.\)

Allusion

Placez les vecteurs sous forme de lignes d'une\(3×3\) matrice, puis calculez le déterminant.

Réponse

\(17\)

Lorsque nous créons une matrice à partir de trois vecteurs, nous devons faire attention à l'ordre dans lequel nous listons les vecteurs. Si nous les listons dans une matrice dans un ordre puis que nous réorganisons les lignes, la valeur absolue du déterminant reste inchangée. Cependant, chaque fois que deux lignes changent de place, le déterminant change de signe :

\(\begin{vmatrix}a_1 & a_2 & a_3\\b_1 & b_2 & b_3\\c_1 & c_2 & c_3\end{vmatrix}=d \quad\quad \begin{vmatrix}b_1 & b_2 & b_3\\a_1 & a_2 & a_3\\c_1 & c_2 & c_3\end{vmatrix}=−d \quad\quad \begin{vmatrix}b_1 & b_2 & b_3\\c_1 & c_2 & c_3\\a_1 & a_2 & a_3\end{vmatrix}=d \quad\quad \begin{vmatrix}c_1 & c_2 & c_3\\b_1 & b_2 & b_3\\a_1 & a_2 & a_3\end{vmatrix}=−d\)

Vérifier ce fait est simple, mais plutôt compliqué. Jetons un coup d'œil à cela avec un exemple :

\ [\ begin {align*} \ begin {vmatrix} 1 et 2 et 1 \ \ −2 & 0 et 3 \ \ 4 et 1 et −1 \ end {vmatrix} &= \ begin {vmatrix} 0 et 3 \ \ 1 et −1 \ end {vmatrix} −2 \ begin {vmatrix} −2 et 3 \ \ 4 et −1 \ end {vmatrix} + \ begin {vmatrix} −2 et 0 \ \ 4 et 1 \ end {vmatrix} \ \ [4 points]
& =( 0−3) −2 (2−12) + (−2−0) \ \ [4 points]
&=−3+20−2=15. \ end {align*} \ nonumber \]

En changeant les deux premières rangées, nous avons

\ [\ begin {align*} \ begin {vmatrix} −2 et 0 et 3 \ \ 1 et 2 et 1 \ \ 4 et 1 \ end {vmatrix} &=-2 \ begin {vmatrix} 2 et 1 \ \ 1 et −1 \ end {vmatrix} +3 \ begin {vmatrix} 1 et 2 \ \ 4 et 1 \ end {vmatrix} \ \ [4pt]
&=−2 (−2−1) +3 (1−8) \ \ [4 points]
&=6−21 = −15. \ end {align*} \ nonumber \]

Réarranger les vecteurs dans les produits triples revient à réorganiser les lignes de la matrice du déterminant. Laissez\(\vecs u=u_1\mathbf{\hat i}+u_2\mathbf{\hat j}+u_3\mathbf{\hat k}, \vecs v=v_1\mathbf{\hat i}+v_2\mathbf{\hat j}+v_3\mathbf{\hat k},\) et\(\vecs w=w_1\mathbf{\hat i}+w_2\mathbf{\hat j}+w_3\mathbf{\hat k}.\) appliquez la note, nous avons

\[\vecs u⋅(\vecs v×\vecs w)=\begin{vmatrix}u_1 & u_2 & u_3\\v_1 & v_2 & v_3\\w_1 & w_2 & w_3\end{vmatrix} \nonumber \]

et

\[\vecs u⋅(\vecs w×\vecs v)=\begin{vmatrix}u_1 & u_2 & u_3\\w_1 & w_2 & w_3\\v_1 & v_2 & v_3\end{vmatrix}. \nonumber \]

Nous pouvons obtenir le déterminant du calcul\(\vecs u⋅(\vecs w×\vecs v)\) en commutant les deux dernières lignes de\(\vecs u⋅(\vecs v×\vecs w).\) Par conséquent,\(\vecs u⋅(\vecs v×\vecs w)=−\vecs u⋅(\vecs w×\vecs v).\)

En suivant ce raisonnement et en explorant les différentes manières d'échanger des variables dans le produit triple scalaire, nous avons obtenu les identités suivantes :

\ [\ begin {align} \ vecs u⋅ (\ vecs v× \ vecs w) &=− \ vecs u⋅ (\ vecs w× \ vecs v) \ \ [10pt]
 \ vecs u⋅ (\ vecs v× \ vecs w) &= \ vecs v⋅ (\ vecs w× \ vecs u) = \ vecs w⋅ (\ vecs u×) vecs (v). \ end {align} \ nonnumber \]

\(\vecs v\)Soit\(\vecs u\) deux vecteurs en position standard. Si\(\vecs u\) et ne\(\vecs v\) sont pas des multiples scalaires les uns des autres, alors ces vecteurs forment les côtés adjacents d'un parallélogramme. Nous avons vu dans Note que l'aire de ce parallélogramme est\(‖\vecs u×\vecs v‖\). Supposons maintenant que nous ajoutions un troisième vecteur\(\vecs w\) qui ne se trouve pas dans le même plan que\(\vecs u\) et\(\vecs v\) partage toujours le même point initial. Ces vecteurs forment ensuite trois arêtes d'un parallélépipède, un prisme tridimensionnel à six faces qui sont chacune des parallélogrammes, comme le montre la figure\(\PageIndex{7}\). Le volume de ce prisme est le produit de la hauteur de la figure et de la surface de sa base. Le produit scalaire triple de\(\vecs u,\vecs v,\) et\(\vecs w\) fournit une méthode simple pour calculer le volume du parallélépipède défini par ces vecteurs.

Volume d'un parallélépipède

Le volume d'un parallélépipède avec des arêtes adjacentes donné par les vecteurs\(\vecs u,\vecs v\), et\(\vecs w\) est la valeur absolue du produit scalaire triple (Figure\(\PageIndex{7}\)) :

\[V=||\vecs u⋅(\vecs v×\vecs w)||. \nonumber \]

Notez que, comme son nom l'indique, le produit triple scalaire produit un scalaire. La formule de volume qui vient d'être présentée utilise la valeur absolue d'une quantité scalaire.

Figure\(\PageIndex{7}\) : La hauteur du parallélépipède est donnée par\(\|\text{proj}_{\vecs v×\vecs w}\vecs u\|.\)

Une preuve

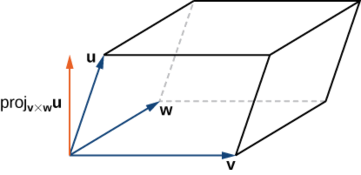
La surface de la base du parallélépipède est donnée par\(‖\vecs v×\vecs w‖.\) La hauteur de la figure est donnée par\(\|\text{proj}_{\vecs v×\vecs w}\vecs u\|.\) Le volume du parallélépipède est le produit de la hauteur et de la surface de la base, nous avons donc

\ [\ begin {align*} V &=\ text {proj} _ {\ vecs v× \ vecs w} \ vecs un1 \ vecs v× \ vecs w× \ vecs wlang=fr \ \ [4pt]
&=\ drac {\ vecs u⋅ (\ vecs v× \ vecs u⋅ (\ vecs v× \ vecs w⋅ (\ vecs v× \ vecs u⋅ (\ vecs v× \ vecs u⋅ (\ vecs v× \ vecs u⋅ (\ vecs v× \ vecs u⋅ (\ vecs v× vecs v× \ vecs w1050 \ \ [4 points]
&= \ | \ vecs u⋅ (\ vecs v× \ vecs w) \ |. \ end {align*} \]

□

Exemple\(\PageIndex{11}\): Calculating the Volume of a Parallelepiped

Laissez\(\vecs u=⟨−1,−2,1⟩,\vecs v=⟨4,3,2⟩,\) et\(\vecs w=⟨0,−5,−2⟩\). Déterminez le volume du parallélépipède avec des arêtes adjacentes\(\vecs u,\vecs v\), et\(\vecs w\) (Figure\(\PageIndex{8}\)).

 ; v = <4, 3, 2> ; et w = <0, -5, -2>." src="https://math.libretexts.org/@api/dek...7777869284.png">

Figurine\(\PageIndex{8}\)

Solution

Nous avons

\ [\ begin {align*} \ vecs u⋅ (\ vecs v× \ vecs w) &= \ begin {vmatrix} −1 et −2 et 1 \ \ 4 et 3 et 2 \ \ 0 et −5 et −2 \ end {vmatrix} \ \ [4pt]
&= (−1) \ begin {vmatrix} 3 et 2 \ \ −5 et −2 \ end {vmatrix} +2 \ begin {vmatrix} 4 et 2 \ \ 0 et −2 \ end {vmatrix} + \ begin {vmatrix} 4 et 3 \ \ 0 et −5 \ end { vmatrix} \ \ [4 points]
& =( −1) (−6+10) +2 (−8−0) + (−20−0) \ \ [4 points]
&=−4−16−20 \ \ [4 points]
&=−40. \ end {align*} \]

Ainsi, le volume du parallélépipède est égal aux\(|−40|=40\) unités ³

Exercice\(\PageIndex{11}\)

Trouvez le volume du parallélépipède formé par les vecteurs\(\vecs a=3\mathbf{\hat i}+4\mathbf{\hat j}−\mathbf{\hat k}, \vecs b=2\mathbf{\hat i}−\mathbf{\hat j}−\mathbf{\hat k},\) et\(\vecs c=3\mathbf{\hat j}+\mathbf{\hat k}.\)

Allusion

Calculez le produit scalaire triple en trouvant un déterminant.

Réponse

\(8\)unités ³

Applications du produit croisé

Le produit croisé apparaît dans de nombreuses applications pratiques en mathématiques, en physique et en ingénierie. Examinons ici certaines de ces applications, y compris la notion de couple, avec laquelle nous avons commencé cette section. D'autres applications apparaîtront dans les chapitres suivants, en particulier dans notre étude des champs vectoriels tels que les champs gravitationnels et électromagnétiques (Introduction au calcul vectoriel).

Exemple\(\PageIndex{12}\): Using the Triple Scalar Product

Utilisez le produit scalaire triple pour montrer que les vecteurs\(\vecs u=⟨2,0,5⟩,\vecs v=⟨2,2,4⟩\) et\(\vecs w=⟨1,−1,3⟩\) sont coplanaires, c'est-à-dire que ces vecteurs se situent dans le même plan.

Solution

Commencez par calculer le produit scalaire triple pour trouver le volume du parallélépipède défini par\(\vecs u,\vecs v,\) et\(\vecs w\) :

\ [\ begin {align*} \ vecs u⋅ (\ vecs v× \ vecs w) &= \ begin {vmatrix} 2 et 0 et 5 \ \ 2 et 4 \ \ 1 et −1 et −1 et 3 \ end {vmatrix} \ \ [4 points]
&= [2) (3) + (0) (4) (1) (1) +5 (2) (−1)] − 5 (2) (1) + (2) (2) (4) (-1) + (0) (2) (3)] \ \ [4 points]
&=2−2 =0. \ end {align*} \]

Le volume du parallélépipède est\(0\) d'unités ³, donc l'une des dimensions doit être nulle. Les trois vecteurs se situent donc tous dans le même plan.

Exercice\(\PageIndex{12}\)

Les vecteurs\(\vecs a=\mathbf{\hat i}+\mathbf{\hat j}−\mathbf{\hat k}, \vecs b=\mathbf{\hat i}−\mathbf{\hat j}+\mathbf{\hat k},\) sont-ils\(\vecs c=\mathbf{\hat i}+\mathbf{\hat j}+\mathbf{\hat k}\) coplanaires ?

Allusion

Calculez le produit scalaire triple.

Réponse

Non, le produit scalaire triple est\(−4≠0,\) tel que les trois vecteurs forment les arêtes adjacentes d'un parallélépipède. Ils ne sont pas coplanaires.

Exemple\(\PageIndex{13}\): Finding an Orthogonal Vector

Un seul plan peut passer par un ensemble de trois points non colinéaires. Trouvez un vecteur orthogonal au plan contenant des points\(P=(9,−3,−2),Q=(1,3,0),\) et\(R=(−2,5,0).\)

Solution

Le plan doit contenir des vecteurs\(\vecd{PQ}\) et\(\vecd{QR}\) :

\(\vecd{PQ}=⟨1−9,3−(−3),0−(−2)⟩=⟨−8,6,2⟩\)

\(\vecd{QR}=⟨−2−1,5−3,0−0⟩=⟨−3,2,0⟩.\)

Le produit croisé\(\vecd{PQ}×\vecd{QR}\) produit un vecteur orthogonal à la fois à\(\vecd{PQ}\) et\(\vecd{QR}\). Par conséquent, le produit croisé est orthogonal au plan qui contient ces deux vecteurs :

\ [\ begin {align*} \ vecd {PQ} × \ vecd {QR} &= \ begin {vmatrix} \ mathbf {\ hat i} & \ mathbf {\ hat j} & \ mathbf {\ hat k} \ \ −8 et 6 et 2 \ \ −3 et 2 et 0 \ end {vmatrix} \ \ [4pt]
&=0 \ mathbf {\ hat i} −6 \ mathbf {\ hat j} −16 \ mathbf {\ hat k} − (−18 \ mathbf {\ hat k} +4 \ mathbf {\ hat i} +0 \ mathbf {\ hat j}) \ \ [4 points]
&=−4 \ mathbf {\ hat i} −6 \ mathbf {\ hat j} +2 \ mathbf {\ hat k}. \ end {align*} \]

Nous avons vu comment utiliser le produit scalaire triple et comment trouver un vecteur orthogonal à un plan. Nous appliquons maintenant le produit croisé à des situations réelles.

Parfois, une force provoque la rotation d'un objet. Par exemple, tourner un tournevis ou une clé crée ce type d'effet de rotation, appelé couple.

Définition : Torque

Le couple\(\vecs \tau\) (la lettre grecque tau) mesure la tendance d'une force à produire une rotation autour d'un axe de rotation. \(\vecs r\)Soit un vecteur dont le point initial est situé sur l'axe de rotation et dont le point terminal est situé au point où la force est appliquée, et que le vecteur\(\vecs F\) représente la force. Le couple est alors égal au produit croisé de\(r\) et\(F\) :

\[\vecs \tau=\vecs r×\vecs F. \nonumber \]

Voir la figure\(\PageIndex{9}\).

Figure\(\PageIndex{9}\) : Le couple mesure la façon dont une force entraîne la rotation d'un objet.

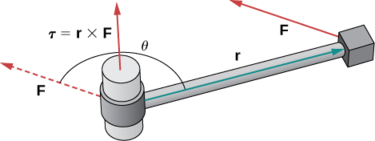
Pensez à utiliser une clé pour serrer un boulon. Le couple τ appliqué au boulon dépend de la force avec laquelle nous poussons la clé (force) et de la distance à laquelle nous appliquons la force sur le manche. Le couple augmente avec l'augmentation de la force exercée sur la clé à une plus grande distance du boulon. Les unités de couple les plus courantes sont le newton-mètre ou le pied-livre. Bien que le couple soit dimensionnellement équivalent au travail (il possède les mêmes unités), les deux concepts sont distincts. Le couple est utilisé spécifiquement dans le contexte de la rotation, alors que le travail implique généralement un mouvement le long d'une ligne.

Exemple\(\PageIndex{14}\): Evaluating Torque

Un boulon est serré en appliquant une force de\(6\) N à une clé de 0,15 m (Figure\(\PageIndex{10}\)). L'angle entre la clé et le vecteur de force est de\(40°\). Déterminez l'amplitude du couple autour du centre du boulon. Arrondissez la réponse à deux décimales.

Figure\(\PageIndex{10}\) : Le couple décrit l'action de torsion de la clé.

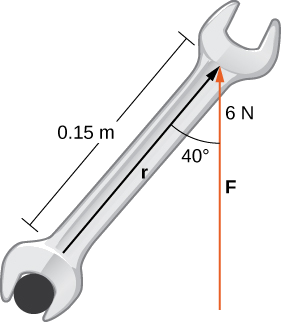
Solution :

Remplacez les informations données dans l'équation définissant le couple :

\ [\ begin {align*}, \ vecs τ&= \ | \ vecs r× \ vecs F \ | \ [4 points]
&=, \ vecs r\ vecs r\ vecs F\ sinθ \ \ [4 points]
& =( 0,15 \, \ text {m}) (6 \, \ text {N}) \ sin 40° \ [4 points]
& =0,58 \, \ text {n⋅m.} \ end {align*} \]

Exercice\(\PageIndex{14}\)

Calculez la force requise pour produire un couple\(15\) N⋅m à un angle égal à\(30º\) celui d'une tige de\(150\) -cm.

Allusion

\(‖\vecs τ‖=15\)N⋅m et\(‖\vecs r‖=1.5\) m

Réponse

\(20\)N

Concepts clés

• Le produit croisé\(\vecs u×\vecs v\) de deux vecteurs\(\vecs u=⟨u_1,u_2,u_3⟩\) et\(\vecs v=⟨v_1,v_2,v_3⟩\) est un vecteur orthogonal à la fois à\(\vecs u\) et\(\vecs v\). Sa longueur est donnée\(‖\vecs u×\vecs v‖=‖\vecs u‖⋅‖\vecs v‖⋅\sin θ,\) par\(θ\) l'angle entre\(\vecs u\) et\(\vecs v\). Sa direction est donnée par la règle de la main droite.
• La formule algébrique pour calculer le produit croisé de deux vecteurs,

\(\vecs u=⟨u_1,u_2,u_3⟩\)et\(\vecs v=⟨v_1,v_2,v_3⟩\), est

\(\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k}.\)

• Le produit croisé satisfait aux propriétés suivantes pour les vecteurs\(\vecs u,\vecs v,\) et\(\vecs w\), et scalaire\(c\) :

\(\vecs u×\vecs v=−(\vecs v×\vecs u)\)

\(\vecs u×(\vecs v+\vecs w)=\vecs u×\vecs v+\vecs u×\vecs w\)

\(c(\vecs u×\vecs v)=(c\vecs u)×\vecs v=\vecs u×(c\vecs v)\)

\(\vecs u×\vecs 0=\vecs 0×\vecs u=\vecs 0\)

\(\vecs v×\vecs v=\vecs 0\)

\(\vecs u⋅(\vecs v×\vecs w)=(\vecs u×\vecs v)⋅\vecs w\)

• Le produit croisé des vecteurs\(\vecs u=⟨u_1,u_2,u_3⟩\) et\(\vecs v=⟨v_1,v_2,v_3⟩\) est le déterminant\(\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\u_1 & u_2 & u_3\\v_1 & v_2 & v_3\end{vmatrix}\)
• Si les vecteurs\(\vecs u\) et\(\vecs v\) forment les côtés adjacents d'un parallélogramme, alors l'aire du parallélogramme est donnée par\(\|\vecs u×\vecs v\|.\)
• Le produit scalaire triple des vecteurs\(\vecs u, \vecs v,\) et\(\vecs w\) est\(\vecs u⋅(\vecs v×\vecs w).\)
• Le volume d'un parallélépipède avec des arêtes adjacentes donné par des vecteurs\(\vecs u,\vecs v\), et\(\vecs w\) est\(V=|\vecs u⋅(\vecs v×\vecs w)|.\)
• Si le produit scalaire triple des vecteurs A\(\vecs u,\vecs v,\) et\(\vecs w\) est nul, alors les vecteurs sont coplanaires. L'inverse est également vrai : si les vecteurs sont coplanaires, leur produit scalaire triple est nul.
• Le produit croisé peut être utilisé pour identifier un vecteur orthogonal à deux vecteurs donnés ou à un plan.
• Le couple\(\vecs τ\) mesure la tendance d'une force à produire une rotation autour d'un axe de rotation. Si la force\(\vecs F\) agit à une distance (déplacement)\(\vecs r\) de l'axe, le couple est égal au produit transversal de\(\vecs r\) et\(\vecs F: \vecs τ=\vecs r×\vecs F.\)

Équations clés

• Le produit croisé de deux vecteurs en termes de vecteurs unitaires

\[\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k} \nonumber \]

Lexique

produit croisé

\(\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k},\)où\(\vecs u=⟨u_1,u_2,u_3⟩\) et\(\vecs v=⟨v_1,v_2,v_3⟩\)

déterminant

un nombre réel associé à une matrice carrée

parallélépipède

un prisme tridimensionnel à six faces qui sont des parallélogrammes

couple

l'effet d'une force qui provoque la rotation d'un objet

produit triple scalaire

le produit scalaire d'un vecteur avec le produit croisé de deux autres vecteurs :\(\vecs u⋅(\vecs v×\vecs w)\)

produit vectoriel

le produit croisé de deux vecteurs