12.1 : Vecteurs dans le plan

Last updated
Save as PDF

Page ID: 197157

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Décrivez un vecteur plan en utilisant la notation correcte.
Effectuez des opérations vectorielles de base (multiplication scalaire, addition, soustraction).
Exprime un vecteur sous forme de composant.
Expliquez la formule de l'amplitude d'un vecteur.
Exprime un vecteur en termes de vecteurs unitaires.
Donnez deux exemples de quantités vectorielles.

Lorsque vous décrivez le mouvement d'un avion en vol, il est important de communiquer deux informations : la direction dans laquelle l'avion se déplace et la vitesse de l'avion. Lors de la mesure d'une force, telle que la poussée des moteurs de l'avion, il est important de décrire non seulement l'intensité de cette force, mais également la direction dans laquelle elle est appliquée. Certaines grandeurs, telles que la force, sont définies à la fois en termes de taille (également appelée magnitude) et de direction. Une quantité qui possède une amplitude et une direction est appelée vecteur. Dans les manuels, les vecteurs sont souvent indiqués par des lettres en gras, telles que$\mathbf{v}$. Comme il est difficile d'écrire en gras clair lorsque nous écrivons des vecteurs à la main, nous inclurons également une flèche ou un harpon au-dessus de la lettre représentant le vecteur. Pour rendre les vecteurs plus clairs dans ce manuel (et pour renforcer la façon dont vous devez les écrire à la main), nous utiliserons généralement des flèches ou des harpons au-dessus des lettres en gras (ou italiques) pour représenter les vecteurs, nous donnant$\vec v$ ou$\vecs{v}$. Notez que certaines figures n'utiliseront toujours que des lettres en gras pour désigner des vecteurs.

Définition : Vecteur

Un vecteur est une quantité qui possède à la fois une amplitude et une direction.

Représentation vectorielle

Un vecteur dans un plan est représenté par un segment de ligne dirigé (flèche). Les extrémités du segment sont appelées point initial et point terminal du vecteur. Une flèche allant du point initial au point terminal indique la direction du vecteur. La longueur du segment de ligne représente sa magnitude. Nous utilisons la notation$\|\vecs{v}\|$ pour indiquer l'amplitude du vecteur$\vecs{v}$. Un vecteur dont le point initial et le point terminal sont identiques est appelé vecteur zéro, désigné$\vecs{0}$. Le vecteur zéro est le seul vecteur sans direction et, par convention, il peut être considéré comme ayant n'importe quelle direction adaptée au problème à résoudre.

Les vecteurs ayant la même amplitude et la même direction sont appelés vecteurs équivalents. Nous traitons les vecteurs équivalents comme égaux, même s'ils ont des points initiaux différents. Ainsi, si$\vecs{v}$ et$\vecs{w}$ sont équivalents, nous écrivons

\[\vecs{v}=\vecs{w}. \nonumber \]

Définition : Vecteurs équivalents

Les vecteurs sont considérés comme des vecteurs équivalents s'ils ont la même amplitude et la même direction.

Les flèches de la figure$\PageIndex{1 (b)}$ sont équivalentes. Chaque flèche a la même longueur et la même direction. Un concept étroitement apparenté est l'idée de vecteurs parallèles. Deux vecteurs sont dits parallèles s'ils ont des directions identiques ou opposées. Nous explorerons cette idée plus en détail plus loin dans le chapitre. Un vecteur est défini par sa magnitude et sa direction, quel que soit l'emplacement de son point initial.

Cette figure comporte deux images. Le premier est étiqueté « a » et comporte un segment de ligne représentant le vecteur v. Le segment de ligne commence au point initial et se dirige vers le point terminal. Il y a une pointe de flèche au point terminal. La deuxième image est étiquetée « b » et comprend cinq vecteurs, chacun étiqueté v sub 1, v sub 2, v sub 3, v sub 4, v sub 5. Ils pointent tous dans la même direction et ont la même longueur. — Figure$\PageIndex{1}$ : (a) Un vecteur est représenté par un segment de ligne dirigé depuis son point initial jusqu'à son point terminal. (b)$\vecs{v}_5$ Les$\vecs{v}_1$ vecteurs sont équivalents.

L'utilisation de lettres minuscules et en gras pour nommer des vecteurs est une représentation courante en caractères imprimés, mais il existe d'autres notations. Lorsque vous écrivez le nom d'un vecteur à la main, par exemple, il est plus facile d'esquisser une flèche au-dessus de la variable que de montrer qu'il s'agit d'un vecteur :$\vec{v}$. Lorsqu'un vecteur possède un point initial$P$ et un point terminal$Q$, la notation$\vecd{PQ}$ est utile car elle indique la direction et l'emplacement du vecteur.

Exemple$\PageIndex{1}$: Sketching Vectors

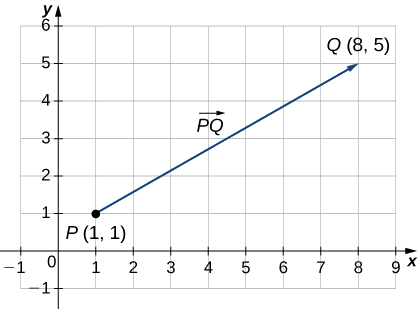
Esquissez un vecteur dans le plan du point initial$P(1,1)$ au point terminal$Q(8,5)$.

Solution

Voir la figure$\PageIndex{2}$. Comme le vecteur va d'un point$P$ à l'autre$Q$, nous le nommons$\vecd{PQ}$.

Cette figure est un graphique du premier quadrant. Un segment de ligne commence à la paire ordonnée (1, 1). De plus, ce point est étiqueté « P ». Le segment de ligne se termine à la paire ordonnée (8, 5) et est étiqueté « Q. » Le segment de ligne est étiqueté « PQ ». — Figure$\PageIndex{2}$ : Le vecteur avec le point initial$(1,1)$ et le point terminal$(8,5)$ est nommé$\vecd{PQ}$.

Exercice$\PageIndex{1}$

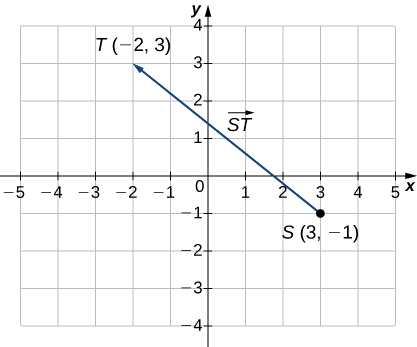
Esquissez le vecteur$\vecd{ST}$ où se$S$ trouve le point$(3,−1)$ et$T$ est le point$(−2,3).$

Allusion: Le premier point indiqué dans le nom du vecteur est le point initial du vecteur.

Réponse: $Cette figure est un graphique du système de coordonnées. Un segment de ligne commence à la paire ordonnée (3, -1). De plus, ce point est étiqueté « S ». Le segment de ligne se termine à la paire ordonnée (-2, 3) et est étiqueté « T ». Il y a une pointe de flèche au point « T », qui représente un vecteur. Le segment de ligne est étiqueté « ST ».$

Combinaison de vecteurs

Les vecteurs ont de nombreuses applications réelles, y compris dans des situations impliquant une force ou une vitesse. Par exemple, considérez les forces qui agissent sur un bateau qui traverse une rivière. Le moteur du bateau génère une force dans une direction et le courant de la rivière génère une force dans une autre direction. Les deux forces sont des vecteurs. Nous devons tenir compte à la fois de l'ampleur et de la direction de chaque force si nous voulons savoir où ira le bateau.

Un deuxième exemple impliquant des vecteurs est celui d'un quarterback qui lance un ballon de football. Le quarterback ne lance pas le ballon parallèlement au sol ; il vise plutôt vers le haut en l'air. La vitesse de son lancer peut être représentée par un vecteur. Si nous connaissons la force avec laquelle il lance la balle (magnitude, dans ce cas, la vitesse) et l'angle (direction), nous pouvons savoir jusqu'où la balle se déplacera sur le terrain.

Un nombre réel est souvent appelé scalaire en mathématiques et en physique. Contrairement aux vecteurs, les scalaires sont généralement considérés comme n'ayant qu'une amplitude, mais aucune direction. La multiplication d'un vecteur par un scalaire modifie l'amplitude du vecteur. C'est ce qu'on appelle la multiplication scalaire. Notez que la modification de l'amplitude d'un vecteur n'indique pas un changement de direction. Par exemple, le vent soufflant du nord au sud peut augmenter ou diminuer de vitesse tout en maintenant sa direction du nord au sud.

Définition : Multiplication scalaire

Le produit$k\vecs{v}$ d'un vecteur$\vecs{v}$ et d'un scalaire$k$ est un vecteur dont l'amplitude est$|k|$ multipliée par l'amplitude de$\vecs{v}$, et dont la direction est identique à la direction de$\vecs{v}$ if$k>0$ et opposée à la direction de$\vecs{v}$ if$k<0$. C'est ce qu'on appelle la multiplication scalaire. Si$k=0$ ou$\vecs{v}=\vecs{0}$, alors$k\vecs{v}=\vecs{0}.$

Comme vous pouvez vous y attendre$k=−1$, si nous désignons le produit$k\vecs{v}$ comme

\[k\vecs{v}=(−1)\vecs{v}=−\vecs{v}. \nonumber \]

Notez qu'il$−\vecs{v}$ a la même amplitude que$\vecs{v}$, mais qu'il a la direction opposée (Figure$\PageIndex{3}$).

Ce graphique comporte 4 figures. La première figure est un vecteur étiqueté « v ». La deuxième figure est un vecteur deux fois plus long que le premier vecteur et est étiquetée « 2 v. » Le troisième chiffre est deux fois moins long que le premier et est étiqueté « 1/2 v. » La quatrième figure est un vecteur dans la direction opposée à la première. Il est étiqueté « -v ». — Figure$\PageIndex{3}$ : (a) Le vecteur d'origine$ \vecs{v}$ possède des$n$ unités de longueur. (b) La longueur des$2n$ unités$2 \vecs{v}$ égales. (c) La longueur de$ \vecs{v}/2$ ses$n/2$ unités. (d) Les vecteurs$\vecs{v}$ et$−\vecs{v}$ ont la même longueur mais des directions opposées.

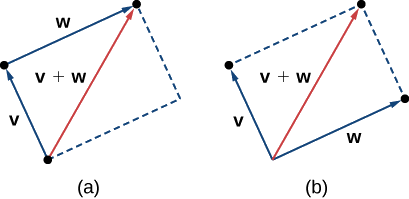
Une autre opération que nous pouvons effectuer sur des vecteurs consiste à les additionner par addition de vecteurs, mais comme chaque vecteur peut avoir sa propre direction, le processus est différent de l'ajout de deux nombres. La méthode graphique la plus courante pour ajouter deux vecteurs consiste à placer le point initial du second vecteur au point terminal du premier, comme sur la figure$\PageIndex{4 (a)}$. Pour comprendre pourquoi cela a du sens, supposons, par exemple, que les deux vecteurs représentent un déplacement. Si un objet se déplace d'abord du point initial au point terminal du vecteur$\vecs{v}$, puis du point initial au point terminal du vecteur$\vecs{w}$, le déplacement global est le même que si l'objet n'avait effectué qu'un seul mouvement du point initial au point terminal du vecteur $\vecs{v}+\vecs{w}$. Pour des raisons évidentes, cette approche est appelée méthode du triangle. Remarquez que si nous avions changé l'ordre, c'$\vecs{w}$était donc notre premier vecteur et$\vecs{v}$ notre deuxième vecteur, nous nous serions retrouvés au même endroit. (Encore une fois, voir Figure$\PageIndex{4 (a)}$.) Ainsi,

\[ \vecs{v}+ \vecs{w}= \vecs{w}+ \vecs{v}. \nonumber \]

Une deuxième méthode d'ajout de vecteurs est appelée méthode du parallélogramme. Avec cette méthode, nous plaçons les deux vecteurs de manière à ce qu'ils aient le même point initial, puis nous dessinons un parallélogramme avec les vecteurs sur deux côtés adjacents, comme sur la figure$\PageIndex{4 (b)}$. La longueur de la diagonale du parallélogramme est la somme. En comparant Figure$\PageIndex{4 (b)}$ et Figure$\PageIndex{4 (a)}$, nous pouvons voir que nous obtenons la même réponse en utilisant l'une ou l'autre méthode. Le vecteur s'$ \vecs{v}+ \vecs{w}$appelle la somme des vecteurs.

Définition : Addition de vecteurs

La somme de deux vecteurs$\vecs{v}$$\vecs{w}$ peut être construite graphiquement en plaçant le point initial de$\vecs{w}$ au point terminal de$\vecs{v}$. Ensuite, la somme des vecteurs$\vecs{v}+\vecs{w}$, est le vecteur dont le point initial coïncide avec le point initial de$\vecs{v}$ et dont le point terminal coïncide avec le point terminal de$\vecs{w}$. Cette opération est connue sous le nom d'addition de vecteurs.

Cette image comporte deux chiffres. Le premier possède deux vecteurs, v et w avec le même point initial. Un parallélogramme est formé en dessinant des lignes discontinues parallèles aux deux vecteurs. Une ligne diagonale est tracée depuis le même point initial jusqu'au coin opposé. Il est étiqueté « v + w ». Le second possède deux vecteurs, v et w. Le vecteur v commence au point terminal du vecteur w. Un parallélogramme est formé en dessinant des lignes discontinues parallèles aux deux vecteurs. Une ligne diagonale est tracée à partir du même point initial que le vecteur w jusqu'au coin opposé. Il est étiqueté « v + w ». — Figure$\PageIndex{4}$ : (a) Lors de l'ajout de vecteurs par la méthode du triangle, le point initial de$\vecs{w}$ est le point terminal de$\vecs{v}$. (b) Lors de l'ajout de vecteurs par la méthode du parallélogramme, les vecteurs$\vecs{v}$ 1 et$\vecs{w}$ 3 ont le même point initial.

Il convient également de discuter ici de la soustraction vectorielle. Nous définissons$\vecs{v}−\vecs{w}$ comme$\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}$. Le vecteur$\vecs{v}−\vecs{w}$ est appelé différence vectorielle. Graphiquement, le vecteur$\vecs{v}−\vecs{w}$ est représenté en traçant un vecteur du point terminal de$\vecs{w}$ au point terminal de$\vecs{v}$ (Figure$\PageIndex{5}$).

Cette image comporte deux chiffres. La première figure comporte deux vecteurs, l'un étiqueté « v » et l'autre « w ». Les deux vecteurs ont le même point initial. Un troisième vecteur est dessiné entre les points terminaux de v et w. Il est étiqueté « v — w ». La deuxième figure comporte deux vecteurs, l'un étiqueté « v » et l'autre « -w ». Le vecteur « -w » a son point initial au point terminal de « v. » Un parallélogramme est créé avec des lignes discontinues où « v » est la diagonale et « w » est la face supérieure. — Figure$\PageIndex{5}$ : (a) La différence vectorielle$\vecs{v}−\vecs{w}$ est illustrée en traçant un vecteur du point terminal de$\vecs{w}$ au point terminal de$\vecs{v}$. (b) Le vecteur$\vecs{v}−\vecs{w}$ est équivalent au vecteur$\vecs{v}+(−\vecs{w})$.

Dans la figure$\PageIndex{4 (a)}$, le point initial de$\vecs{v}+\vecs{w}$ est le point initial de$\vecs{v}$. Le point terminal de$\vecs{v}+\vecs{w}$ est le point terminal de$\vecs{w}$. Ces trois vecteurs forment les côtés d'un triangle. Il s'ensuit que la longueur d'un côté est inférieure à la somme des longueurs des côtés restants. Nous avons donc

\[\|\vecs{v}+\vecs{w}\|≤\|\vecs{v}\|+\|\vecs{w}\|. \nonumber \]

C'est ce que l'on appelle plus généralement l'inégalité triangulaire. Il existe toutefois un cas où le vecteur résultant$\vecs{u}+\vecs{v}$ a la même amplitude que la somme des magnitudes de$\vecs{u}$ et$\vecs{v}$. Cela se produit uniquement lorsque$\vecs{u}$ et$\vecs{v}$ dans la même direction.

Exemple$\PageIndex{2}$: Combining Vectors

À partir des vecteurs$\vecs{v}$ et$\vecs{w}$ illustrés sur la figure$\PageIndex{6}$, esquissez les vecteurs

$3\vecs{w}$
$\vecs{v}+\vecs{w}$
$2\vecs{v}−\vecs{w}$

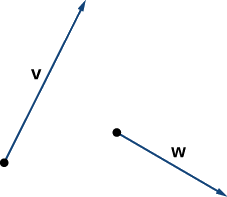
Ce chiffre comporte deux vecteurs. Ce sont les vecteurs v et w. Ils ne sont pas connectés. — Figure$\PageIndex{6}$ : Vecteurs$\vecs{v}$ et$\vecs{w}$ position sur le même plan.

Solution

a. Le vecteur$3\vecs{w}$ a la même direction que$\vecs{w}$ ; il est trois fois plus long que$\vecs{w}$.

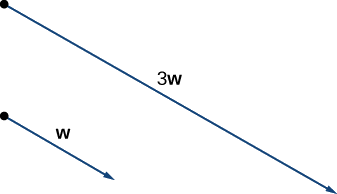
$Ce chiffre comporte deux vecteurs. Le premier est étiqueté « w ». Le second est parallèle à « w » et est étiqueté « 3w ». Il est trois fois plus long que w dans la même direction.$

Le vecteur$3\vecs{w}$ a la même direction$\vecs{w}$ et est trois fois plus long.

b. Utilisez l'une ou l'autre des méthodes d'addition pour trouver$\vecs{v}+\vecs{w}$.

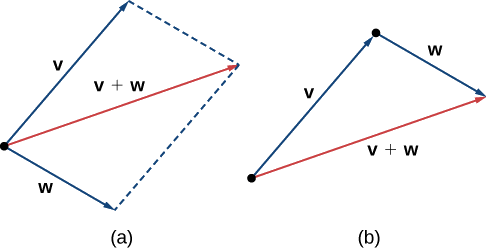
Cette image comporte deux chiffres. Le premier possède deux vecteurs, étiquetés « v » et « w ». Ils ont tous deux le même point de départ. Un troisième vecteur est dessiné, intitulé « v + w ». Il s'agit de la diagonale du parallélogramme formée par des côtés parallèles aux vecteurs v et w. La deuxième figure est un triangle formé par le vecteur v sur un côté et le vecteur w adjacent à v. Le point terminal de v est le point initial de w. Le troisième côté est étiqueté « v + w ». — Figure$\PageIndex{7}$ : Pour trouver$\vecs{v}+\vecs{w}$, alignez les vecteurs à leurs points initiaux ou placez le point initial d'un vecteur au point terminal de l'autre. (a) Le vecteur$\vecs{v}+\vecs{w}$ est la diagonale du parallélogramme avec les côtés$\vecs{v}$ et$\vecs{w}$. (b) Le vecteur$\vecs{v}+\vecs{w}$ est le troisième côté d'un triangle formé avec$\vecs{w}$ placé au point terminal de$\vecs{v}$.

c. Pour le trouver$2\vecs{v}−\vecs{w}$, nous pouvons d'abord réécrire l'expression sous la forme$2\vecs{v}+(−\vecs{w})$. Ensuite, nous pouvons dessiner le vecteur$−\vecs{w}$, puis l'ajouter au vecteur$2\vecs{v}$.

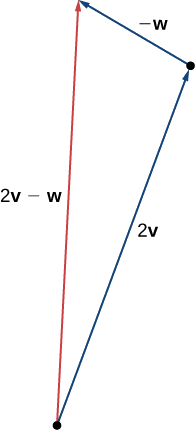
Cette figure est un triangle formé en ayant le vecteur 2v sur un côté et le vecteur -w adjacent à 2v. Le point terminal de 2v est le point initial de -w. La troisième face est étiquetée « 2v - w ». — Figure$\PageIndex{8}$ : Pour le trouver$2\vecs{v}−\vecs{w}$, il suffit d'ajouter$2\vecs{v}+(−\vecs{w})$.

Exercice$\PageIndex{2}$

En utilisant des vecteurs$\vecs{v}$ et$\vecs{w}$ à partir de l'exemple$\PageIndex{2}$, esquissez le vecteur$2\vecs{w}−\vecs{v}$.

Allusion: Premiers vecteurs d'esquisse$2\vecs{w}$ et$−\vecs{v}$.

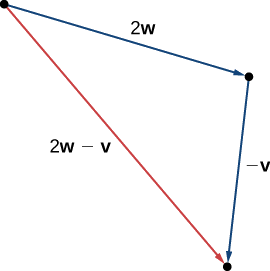
Réponse: $Cette figure est un triangle formé en ayant le vecteur 2w sur un côté et le vecteur -v adjacent à 2w. Le point terminal de 2w est le point initial de -v. La troisième face est étiquetée « 2w — v. »$

Composants vectoriels

Il est plus facile de travailler avec des vecteurs dans un plan lorsque nous travaillons dans un système de coordonnées. Lorsque les points initiaux et terminaux des vecteurs sont donnés en coordonnées cartésiennes, les calculs deviennent simples.

Exemple$\PageIndex{3}$: Comparing Vectors

Sont-ils$\vecs{v}$ des vecteurs$\vecs{w}$ équivalents ?

un.

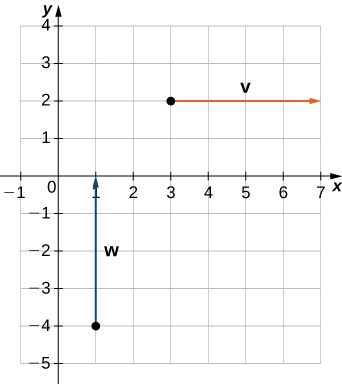
$\vecs{v}$possède un point initial$(3,2)$ et un point terminal$(7,2)$
$\vecs{w}$possède un point initial$(1,−4)$ et un point terminal$(1,0)$

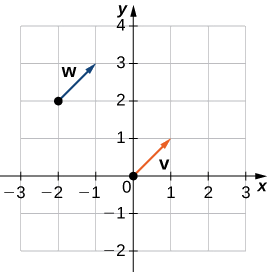
$\vecs{v}$possède un point initial$(0,0)$ et un point terminal$(1,1)$
$\vecs{w}$possède un point initial$(−2,2)$ et un point terminal$(−1,3)$

Solution

a. Les vecteurs ont chacun une$4$ unité de long, mais ils sont orientés dans des directions différentes. Donc$\vecs{v}$ et ne$\vecs{w}$ sont pas équivalents (Figure$\PageIndex{9}$).

Cette figure est un système de coordonnées cartésien à deux vecteurs. Le premier vecteur étiqueté « v » a un point initial en (3, 2) et un point terminal (7, 2). Il est parallèle à l'axe X. Le second vecteur est étiqueté « w » et possède un point initial (1, -4) et un point terminal (1, 0). Il est parallèle à l'axe Y. — Figure$\PageIndex{9}$ : Ces vecteurs ne sont pas équivalents.

b. Sur la base de la figure$\PageIndex{10}$, et en utilisant un peu de géométrie, il est clair que ces vecteurs ont la même longueur et la même direction, donc$\vecs{v}$$\vecs{w}$ sont équivalents.

Cette figure est un système de coordonnées cartésien à deux vecteurs. Le premier vecteur étiqueté « v » a un point initial à (0, 0) et un point terminal (1, 1). Le second vecteur est étiqueté « w » et possède un point initial (-2, 2) et un point terminal (-1, 3). — Figure$\PageIndex{10}$ : Ces vecteurs sont équivalents.

Exercice$\PageIndex{3}$

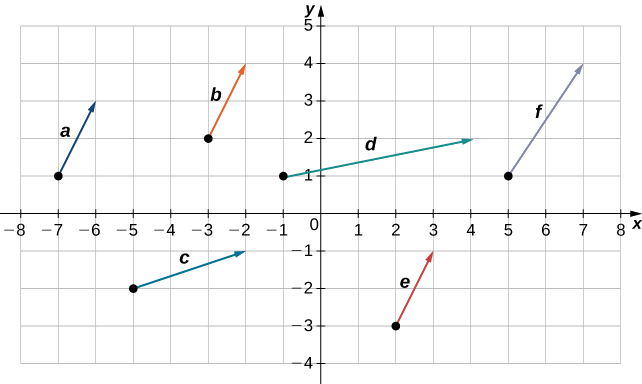
Parmi les vecteurs suivants, lesquels sont équivalents ?

$Cette figure est un système de coordonnées composé de 6 vecteurs, chacun étiqueté de a à f. Trois des vecteurs, « a », « b » et « e », ont la même longueur et pointent dans la même direction.$

Allusion: Les vecteurs équivalents ont à la fois la même amplitude et la même direction.

Réponse: Vecteurs$\vecs{a}, \vecs{b}$, et$\vecs{e}$ sont équivalents.

Nous avons vu comment tracer un vecteur lorsque l'on nous donne un point initial et un point terminal. Toutefois, comme un vecteur peut être placé n'importe où dans un plan, il peut être plus facile d'effectuer des calculs avec un vecteur lorsque son point initial coïncide avec l'origine. Nous appelons vecteur de position standard un vecteur dont le point initial est à l'origine. Comme le point initial de tout vecteur en position standard est connu pour être$(0,0)$, nous pouvons décrire le vecteur en examinant les coordonnées de son point terminal. Ainsi, si le vecteur$\vecs{v}$ a son point initial à l'origine et son point terminal à l'origine,$(x,y),$ nous écrivons le vecteur sous forme de composant comme

\[\vecs{v}=⟨x,y⟩. \nonumber \]

Lorsqu'un vecteur est écrit sous forme de composant de cette manière, les scalaires x et y sont appelés les composants de$\vecs{v}$.

Définition : composants vectoriels

Le vecteur avec le point initial$(0,0)$ et le point terminal$(x,y)$ peut être écrit sous forme de composant comme

\[\vecs{v}=⟨x,y⟩. \nonumber \]

Les scalaires$x$ et$y$ sont appelés les composants de$\vecs{v}$.

N'oubliez pas que les vecteurs sont nommés avec des lettres minuscules en gras ou en traçant une flèche au-dessus de leur nom. Nous avons également appris que nous pouvons nommer un vecteur par sa forme constitutive, avec les coordonnées de son point terminal entre crochets angulaires. Cependant, lors de l'écriture de la forme constitutive d'un vecteur, il est important de faire la distinction entre$⟨x,y⟩$ et$(x,y)$. La première paire ordonnée utilise des crochets angulaires pour décrire un vecteur, tandis que la seconde utilise des parenthèses pour décrire un point dans un plan. Le point initial de$⟨x,y⟩$ est$(0,0)$ ; le point terminal de$⟨x,y⟩$ est$(x,y)$.

Lorsque nous avons un vecteur qui n'est pas déjà en position standard, nous pouvons déterminer la forme de sa composante de deux manières. Nous pouvons utiliser une approche géométrique, dans laquelle nous esquissons le vecteur dans le plan de coordonnées, puis nous esquissons un vecteur de position standard équivalent. Alternativement, nous pouvons le trouver algébriquement, en utilisant les coordonnées du point initial et du point terminal. Pour le trouver algébriquement, nous soustrayons la$x$ coordonnée -du point initial de la$x$ coordonnée -du point terminal pour obtenir la$x$ composante -, et nous soustrayons la$y$ coordonnée -du point initial de la$y$ coordonnée -du point terminal pour obtenir le$y$ -composant.

Règle : Forme constitutive d'un vecteur

$\vecs{v}$Soit un vecteur avec un point initial$(x_i,y_i)$ et un point terminal$(x_t,y_t)$. Ensuite, nous pouvons exprimer$\vecs{v}$ sous forme de composant comme$\vecs{v}=⟨x_t−x_i,y_t−y_i⟩$.

Exemple$\PageIndex{4}$: Expressing Vectors in Component Form

Vecteur express$\vecs{v}$ avec point initial$(−3,4)$ et point$(1,2)$ terminal sous forme de composant.

Solution :

a. Géométrique

1. Esquissez le vecteur dans le plan de coordonnées (Figure$\PageIndex{11}$).

2. Le point terminal se trouve à 4 unités vers la droite et à 2 unités plus bas par rapport au point initial.

3. Trouvez le point situé à 4 unités vers la droite et à 2 unités plus bas par rapport à l'origine.

4. En position standard, ce vecteur possède un point initial$(0,0)$ et un point terminal$(4,−2)$ :

$\vecs{v}=⟨4,−2⟩.$

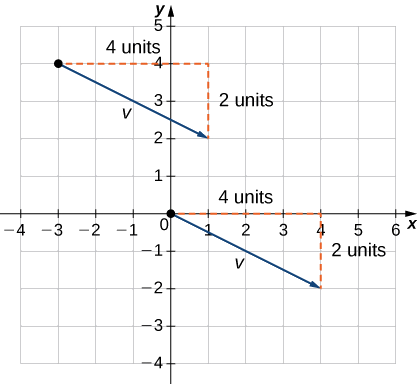
Cette figure est un système de coordonnées. Il y a deux vecteurs sur le graphique. Le premier vecteur a un point initial à l'origine et un point terminal à (4, -2). La distance horizontale entre le point initial et le point terminal du vecteur est étiquetée comme « 4 unités ». La distance verticale entre le point initial et le point terminal est étiquetée comme « 2 unités ». Le deuxième vecteur a un point initial à (-3, 4) et un point terminal à (1, 2). La distance horizontale entre le point initial et le point terminal du vecteur est étiquetée comme « 4 unités ». La distance verticale entre le point initial et le point terminal est étiquetée comme « 2 unités ». — Figure$\PageIndex{11}$ : Ces vecteurs sont équivalents.

b. Algébrique

Dans la première solution, nous avons utilisé un croquis du vecteur pour voir que le point terminal se trouve à 4 unités vers la droite. Nous pouvons y parvenir de manière algébrique en trouvant la différence entre les$x$ coordonnées :

$x_t−x_i=1−(−3)=4.$

De même, la différence des$y$ coordonnées indique la longueur verticale du vecteur.

$y_t−y_i=2−4=−2.$

Donc, sous forme de composant,

$\vecs{v}=⟨x_t−x_i,y_t−y_i⟩=⟨1−(−3),2−4⟩=⟨4,−2⟩.$

Exercice$\PageIndex{4}$

$\vecs{w}$Le vecteur possède un point initial$(−4,−5)$ et un point terminal$(−1,2)$. Express$\vecs{w}$ sous forme de composant.

Allusion: Vous pouvez utiliser la méthode géométrique ou algébrique.

Réponse: $⟨3,7⟩$

Pour déterminer l'amplitude d'un vecteur, nous calculons la distance entre son point initial et son point terminal. L'amplitude du vecteur$\vecs{v}=⟨x,y⟩$ est notée$\|\vecs{v}\|,$ ou$|\vecs{v}|$, et peut être calculée à l'aide de la formule

\[\|\vecs{v}\|=\sqrt{x^2+y^2}. \nonumber \]

Notez que, comme ce vecteur est écrit sous forme de composant, il est équivalent à un vecteur en position standard, avec son point initial à l'origine et au point terminal$(x,y)$. Il suffit donc de calculer l'amplitude du vecteur en position standard. En utilisant la formule de distance pour calculer la distance entre le point initial$(0,0)$ et le point terminal$(x,y)$, nous avons

\[\|\vecs{v}\|=\sqrt{(x−0)^2+(y−0)^2}=\sqrt{x^2+y^2}. \nonumber \]

Sur la base de cette formule, il est clair que pour n'importe quel vecteur$\vecs{v}, \|\vecs{v}\|≥0,$ et$\|\vecs{v}\|=0$ si et seulement si$\vecs{v}=\vecs{0}$.

L'amplitude d'un vecteur peut également être dérivée à l'aide du théorème de Pythagore, comme dans la figure suivante.

Cette figure est un triangle droit. Les deux faces sont étiquetées « x » et « y ». L'hypoténuse est représentée sous forme de vecteur et est étiquetée « racine carrée (x^2 + y^2) ». — Figure$\PageIndex{12}$ : Si vous utilisez les composantes d'un vecteur pour définir un triangle droit, l'amplitude du vecteur correspond à la longueur de l'hypoténuse du triangle.

Nous avons défini la multiplication scalaire et l'addition de vecteurs de manière géométrique. L'expression de vecteurs sous forme de composants nous permet d'effectuer ces mêmes opérations de manière algébrique.

Définition : Multiplication scalaire et addition de vecteurs

Laissons$\vecs{v}=⟨x_1,y_1⟩$ et$\vecs{w}=⟨x_2,y_2⟩$ soyez des vecteurs, et$k$ soyez un scalaire.

Multiplication scalaire :\[k\vecs{v}=⟨kx_1,ky_1⟩ \nonumber \]
Ajout de vecteurs :\[\vecs{v}+\vecs{w}=⟨x_1,y_1⟩+⟨x_2,y_2⟩=⟨x_1+x_2,y_1+y_2⟩ \nonumber \]

Exemple$\PageIndex{5}$: Performing Operations in Component Form

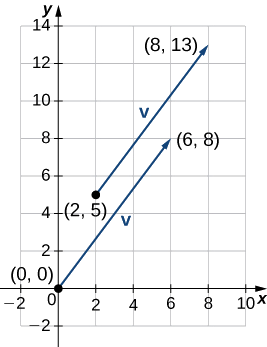
$\vecs{v}$Soit le vecteur avec le point initial$(2,5)$ et le point terminal$(8,13)$, et soit$\vecs{w}=⟨−2,4⟩$.

Exprimez$\vecs{v}$ sous forme de composant et trouvez$\|\vecs{v}\|$. Ensuite, en utilisant l'algèbre, trouvez
$\vecs{v}+\vecs{w}$,
$3\vecs{v}$, et
$\vecs{v}−2\vecs{w}$.

Solution

a. Pour placer le point initial de$\vecs{v}$ à l'origine, nous devons traduire le vecteur 2 unités vers la gauche et 5 unités vers le bas (Figure$\PageIndex{13}$). En utilisant la méthode algébrique, nous pouvons exprimer$\vecs{v}$ comme$\vecs{v}=⟨8−2,13−5⟩=⟨6,8⟩$ suit :

$\|\vecs{v}\|=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10$.

Cette figure représente le premier quadrant d'un système de coordonnées. Il possède deux vecteurs. Le premier vecteur possède un point initial en (2, 5) et un point terminal (8, 13). Le second vecteur a un point initial à l'origine et un point terminal à (6, 8). — Figure$\PageIndex{13}$ : Sous forme de composant,$\vecs{v}=⟨6,8⟩$.

b. Pour rechercher$\vecs{v}+\vecs{w}$, ajoutez les$x$ composants et les$y$ composants séparément :

$\vecs{v}+\vecs{w}=⟨6,8⟩+⟨−2,4⟩=⟨4,12⟩.$

c. Pour trouver$3\vecs{v}$, multipliez$\vecs{v}$ par le scalaire$k=3$ :

$3\vecs{v}=3⋅⟨6,8⟩=⟨3⋅6,3⋅8⟩=⟨18,24⟩.$

d. Pour le trouver$\vecs{v}−2\vecs{w}$, le trouver$−2\vecs{w}$ et l'ajouter à$\vecs{v}:$

$\vecs{v}−2\vecs{w}=⟨6,8⟩−2⋅⟨−2,4⟩=⟨6,8⟩+⟨4,−8⟩=⟨10,0⟩.$

Exercice$\PageIndex{5A}$

Soit$\vecs{a}=⟨7,1⟩$ et$\vecs{b}$ soit le vecteur avec le point initial$(3,2)$ et le point terminal$(−1,−1).$

Trouve$\|\vecs{a}\|$.
Express$\vecs{b}$ sous forme de composant.
Trouvez$3\vecs{a}−4\vecs{b}.$

Allusion: Utilisez le théorème de Pythagore pour trouver$\|\vecs{a}\|$. Pour trouver$3\vecs{a}−4\vecs{b}$, commencez par trouver les multiples scalaires$3\vecs{a}$ et$−4\vecs{b}$.

Répondez à une: $\|\vecs{a}\|=5\sqrt{2},$
Réponse b: $\vecs{b}=⟨−4,−3⟩,$
Réponse c: $3\vecs{a}−4\vecs{b}=⟨37,15⟩$

Maintenant que nous avons établi les règles de base de l'arithmétique vectorielle, nous pouvons énoncer les propriétés des opérations vectorielles. Nous allons prouver deux de ces propriétés. Les autres peuvent être prouvés de la même manière.

Propriétés des opérations vectorielles

Laissez$\vecs{u}, \, \vecs{v}$ et$\vecs{w}$ soyez des vecteurs dans un plan. Laissons$r$ et$s$ soyez des scalaires.

Propriété commutative\[\vecs{u}+\vecs{v}=\vecs{v}+\vecs{u} \label{commutative} \]
Propriété associative\[(\vecs{u}+\vecs{v})+\vecs{w}=\vecs{u}+(\vecs{v}+\vecs{w}) \nonumber \]
Propriété d'identité additive\[\vecs{u}+\vecs{0}=\vecs{u} \nonumber \]
Propriété inverse additive\[\vecs{u}+(−\vecs{u})=\vecs{0} \nonumber \]
Associativité de la multiplication scalaire\[r(s\vecs{u})=(rs)\vecs{u} \nonumber \]
Propriété distributive\[(r+s)\vecs{u}=r\vecs{u}+s\vecs{u} \label{Distributive} \]
Propriété distributive\[r(\vecs{u}+\vecs{v})=r\vecs{u}+r\vecs{v} \nonumber \]
Identité et zéro propriété\[1\vecs{u}=\vecs{u}, \, 0\vecs{u}=\vecs{0} \nonumber \]

Preuve de propriété commutative

$\vecs{u}=⟨x_1,y_1⟩$Let et$\vecs{v}=⟨x_2,y_2⟩.$ appliquez la propriété commutative pour les nombres réels :

\[ \begin{align*} \vecs{u}+\vecs{v} =⟨x_1+x_2,y_1+y_2⟩ \\[4pt] = ⟨x_2+x_1,y_2+y_1⟩ \\[4pt] = \vecs{v}+\vecs{u}. \end{align*}\]

□

Preuve de propriété distributive

Appliquez la propriété distributive pour les nombres réels :

\[ \begin{align*} r(\vecs{u}+\vecs{v}) =r⋅⟨x_1+x_2,y_1+y_2⟩ \\[4pt] =⟨r(x_1+x_2),r(y_1+y_2)⟩ \\[4pt] = ⟨rx_1+rx_2,ry_1+ry_2⟩ \\[4pt] = ⟨rx_1,ry_1⟩+⟨rx_2,ry_2⟩ \\[4pt] = r\vecs{u}+r\vecs{v}. \end{align*}\]

□

Exercice$\PageIndex{5B}$

Prouvez la propriété inverse additive.

Allusion: Utilisez la forme des composants des vecteurs.

Nous avons trouvé les composantes d'un vecteur en fonction de ses points initial et terminal. Dans certains cas, il se peut que nous n'ayons que l'amplitude et la direction d'un vecteur, et non les points. Pour ces vecteurs, nous pouvons identifier les composantes horizontales et verticales à l'aide de la trigonométrie (Figure$\PageIndex{14}$).

Cette figure est un triangle droit. Il existe un angle étiqueté thêta. Les deux faces sont étiquetées « magnitude de v fois le thêta cosinus » et « magnitude de v fois le thêta sinusoïdal ». L'hypoténuse est étiquetée « magnitude de v. » — Figure$\PageIndex{14}$ : Les composantes d'un vecteur forment les branches d'un triangle droit, le vecteur représentant l'hypoténuse.

Considérez l'angle$θ$ formé par le vecteur$\vecs{v}$ et l'$x$axe positif. Nous pouvons voir sur le triangle quelles$\vecs{v}$ sont les composantes du vecteur$⟨\|\vecs{v}\| \cos{θ}, \, \|\vecs{v}\| \sin {θ}⟩$. Par conséquent, étant donné un angle et la magnitude d'un vecteur, nous pouvons utiliser le cosinus et le sinus de l'angle pour trouver les composantes du vecteur.

Exemple$\PageIndex{6}$: Finding the Component Form of a Vector Using Trigonometry

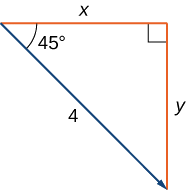
Détermine la forme constitutive d'un vecteur de magnitude 4 qui forme un angle de$−45°$ avec l'$x$axe.

Solution

Supposons$x$ et$y$ représentez les composantes du vecteur (Figure$\PageIndex{15}$). Puis$x=4 \cos(−45°)=2 \sqrt{2}$ et$y=4 \sin(−45°)=−2\sqrt{2}$. La forme constitutive du vecteur est$⟨2\sqrt{2},−2\sqrt{2}⟩$.

Cette figure est un triangle droit. Les deux faces sont étiquetées « x » et « y ». L'hypoténuse est étiquetée « 4 ». Il existe également un angle étiqueté « 45 degrés ». L'hypoténuse est représentée sous forme de vecteur. — Figure$\PageIndex{15}$ : Utilisez des rapports trigonométriques$x=\|\vecs{v}\| \cos θ$ et *$y=\|\vecs{v}\| \sin θ,$*identifiez les composantes du vecteur.

Exercice$\PageIndex{6}$

Trouvez la forme constitutive du vecteur$\vecs{v}$ de magnitude 10 qui forme un angle de$120°$ avec l'axe positif$x$.

Allusion: $x=\|\vecs{v}\| \cos θ$et$y=\|\vecs{v}\| \sin θ$
Réponse: $\vecs v=⟨−5,5\sqrt{3}⟩$

Vecteurs unitaires

Un vecteur unitaire est un vecteur avec une amplitude$1$. Pour tout vecteur différent de zéro$\vecs{v}$, nous pouvons utiliser la multiplication scalaire pour trouver un vecteur$\vecs{u}$ unitaire ayant la même direction que$\vecs{v}$. Pour ce faire, on multiplie le vecteur par l'inverse de sa magnitude :

\[\vecs{u}=\dfrac{1}{\|\vecs{v}\|} \vecs{v}. \nonumber \]

Rappelons que lorsque nous avons défini la multiplication scalaire, nous l'avons noté$\|k\vecs{v}\| =|k|⋅\|\vecs{v}\| $. Car$\vecs{u}=\dfrac{1}{\|\vecs{v}\| }\vecs{v}$, il s'ensuit que$\|\vecs{u}\| =\dfrac{1}{\|\vecs{v}\| }(\|\vecs{v}\| )=1$. Nous disons que$\vecs{u}$ c'est le vecteur unitaire dans la direction de$\vecs{v}$ (Figure$\PageIndex{16}$). Le processus d'utilisation de la multiplication scalaire pour trouver un vecteur unitaire dans une direction donnée est appelé normalisation.

Cette image comporte deux chiffres. Le premier est un vecteur étiqueté « v ». La deuxième figure est un vecteur dans la même direction nommé « u ». Ce vecteur a une longueur de 1 unité. — Figure$\PageIndex{16}$ : Le vecteur$\vecs{v}$ et le vecteur unitaire associé$\vecs{u}=\dfrac{1}{\|\vecs{v}\|}\vecs{v}$. Dans ce cas,$\|\vecs{v}\|>1.$

Exemple$\PageIndex{7}$: Finding a Unit Vector

Laissez$\vecs{v}=⟨1,2⟩$.

Trouvez un vecteur unitaire ayant la même direction que$\vecs{v}$.
Trouvez un vecteur$\vecs{w}$ ayant la même direction$\vecs{v}$ que$\|\vecs{w}\|=7$.

Solution :

a. Déterminez d'abord la magnitude de$\vecs{v}$, puis divisez les composantes de$\vecs{v}$ par la magnitude :

\[\|\vecs{v}\|=\sqrt{1^2+2^2}=\sqrt{1+4}=\sqrt{5} \nonumber \]

\[\vecs{u}=\dfrac{1}{\|\vecs{v}\|}\vecs{v}=\dfrac{1}{\sqrt{5}}⟨1,2⟩=⟨\dfrac{1}{\sqrt{5}},\dfrac{2}{\sqrt{5}}⟩ \nonumber. \nonumber \]

b. Le vecteur$\vecs{u}$ est dans la même direction que$\vecs{v}$ et$\|\vecs{u}\|=1$. Utilisez la multiplication scalaire pour augmenter la longueur de$\vecs{u}$ sans changer de direction :

\[\vecs{w}=7\vecs{u}=7⟨\dfrac{1}{\sqrt{5}},\dfrac{2}{\sqrt{5}}⟩=⟨\dfrac{7}{\sqrt{5}},\dfrac{14}{\sqrt{5}}⟩ \nonumber. \nonumber \]

Exercice$\PageIndex{7}$

Laissez$\vecs{v}=⟨9,2⟩$. Trouvez un vecteur dont l'amplitude$5$ est dans la direction opposée à$\vecs{v}$.

Allusion: Tout d'abord, trouvez un vecteur unitaire dans la même direction que$\vecs{v}$.
Réponse: $⟨−\dfrac{45}{\sqrt{85}},−\dfrac{10}{\sqrt{85}}⟩$

Nous avons vu à quel point il peut être pratique d'écrire un vecteur sous forme de composant. Parfois, cependant, il est plus pratique d'écrire un vecteur comme la somme d'un vecteur horizontal et d'un vecteur vertical. Pour vous faciliter la tâche, examinons les vecteurs unitaires standard. Les vecteurs unitaires standard sont les vecteurs$\hat{\mathbf i}=⟨1,0⟩$ et$\hat{\mathbf j}=⟨0,1⟩$ (Figure$\PageIndex{17}$).

Cette figure présente les axes x et y d'un système de coordonnées dans le premier quadrant. Sur l'axe des abscisses se trouve un vecteur intitulé « i », qui est égal à <1,0 — Figure$\PageIndex{17}$ : Les vecteurs unitaires standard$\hat{\mathbf i}$ et$\hat{\mathbf j}$.

En appliquant les propriétés des vecteurs, il est possible d'exprimer n'importe quel vecteur en termes$\hat{\mathbf i}$ et$\hat{\mathbf j}$ selon ce que nous appelons une combinaison linéaire :

\[\vecs{v}=⟨x,y⟩=⟨x,0⟩+⟨0,y⟩=x⟨1,0⟩+y⟨0,1⟩=x\hat{\mathbf i}+y\hat{\mathbf j}. \nonumber \]

Ainsi,$\vecs{v}$ est la somme d'un vecteur horizontal avec amplitude$x$ et d'un vecteur vertical avec amplitude$y$, comme dans la Figure$\PageIndex{18}$.

Cette figure est un triangle droit. Le côté horizontal est étiqueté « xi ». Le côté vertical est étiqueté « yj ». L'hypoténuse est un vecteur marqué « v ». — Figure$\PageIndex{18}$ : Le vecteur$\vecs{v}$ est la somme de$x\hat{\mathbf i}$ et$y\hat{\mathbf j}$.

Exemple$\PageIndex{8}$: Using Standard Unit Vectors

Exprimez le vecteur$\vecs{w}=⟨3,−4⟩$ en termes de vecteurs unitaires standard.
$\vecs{u}$Le vecteur est un vecteur unitaire qui forme un angle de$60°$ avec l'$x$axe positif. Utilisez des vecteurs unitaires standard pour décrire$\vecs{u}$.

Solution :

a. Résolvez$\vecs{w}$ le vecteur en un vecteur avec une$y$ composante nulle et un vecteur avec une$x$ composante nulle :

\[\vecs{w}=⟨3,−4⟩=3 \hat{\mathbf i}−4 \hat{\mathbf j}. \nonumber \]

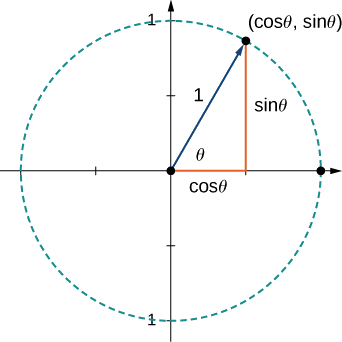
b. Comme il$\vecs{u}$ s'agit d'un vecteur unitaire, le point terminal se trouve sur le cercle unitaire lorsque le vecteur est placé en position standard (Figure$\PageIndex{19}$).

\[ \begin{align*} \vecs{u} =⟨\cos 60°,\sin 60°⟩ \\[4pt] =⟨\dfrac{1}{2},\dfrac{\sqrt{3}}{2}⟩ \\[4pt] = \dfrac{1}{2} \hat{\mathbf i}+\dfrac{\sqrt{3}}{2} \hat{\mathbf j}. \end{align*}\]

Ce chiffre est une unité de cercle. Il s'agit d'un cercle centré à l'origine. Il possède un vecteur avec un point initial à l'origine et un point terminal sur le cercle. Le point terminal est étiqueté (cos (theta), sin (theta)). La longueur du vecteur est de 1 unité. Il existe également un triangle droit formé avec le vecteur comme hypoténuse. Le côté horizontal est étiqueté « cos (thêta) » et le côté vertical est étiqueté « sin (thêta) ». — Figure$\PageIndex{19}$ : Le point terminal de$\vecs{u}$ se trouve sur le cercle unitaire$(\cos θ, \sin θ)$.

Exercice$\PageIndex{8}$

$\vecs{b}$Soit$\vecs{a}=⟨16,−11⟩$ un vecteur unitaire qui forme un angle de$225°$ avec l'$x$axe positif. $\vecs{a}$Exprime et$\vecs{b}$ en termes de vecteurs unitaires standard.

Allusion: Utilisez le sinus et le cosinus pour trouver les composants de$\vecs{b}$.
Réponse: $\vecs{a}=16 \hat{\mathbf i}−11 \hat{\mathbf j}, \quad \vecs{b}=−\dfrac{\sqrt{2}}{2} \hat{\mathbf i}−\dfrac{\sqrt{2}}{2} \hat{\mathbf j}$

Applications des vecteurs

Comme les vecteurs ont à la fois une direction et une amplitude, ils constituent des outils précieux pour résoudre des problèmes impliquant des applications telles que le mouvement et la force. Souvenez-vous de l'exemple du bateau et de l'exemple du quarterback que nous avons décrits précédemment Nous examinons ici deux autres exemples en détail.

Exemple$\PageIndex{9A}$: Finding Resultant Force

La voiture de Jane est coincée dans la boue. Lisa et Jed arrivent dans un camion pour l'aider à sortir. Ils fixent une extrémité d'une sangle de remorquage à l'avant de la voiture et l'autre extrémité à l'attache de remorque du camion, et le camion commence à tirer. Pendant ce temps, Jane et Jed se mettent derrière la voiture et poussent. Le camion génère une force horizontale de 300 livres sur la voiture. Jane et Jed poussent légèrement vers le haut et génèrent une force de 150 livres sur la voiture. Ces forces peuvent être représentées par des vecteurs, comme le montre la figure$\PageIndex{20}$. L'angle entre ces vecteurs est de 15°. Trouvez la force résultante (la somme vectorielle) et donnez sa magnitude au dixième de livre le plus proche et son angle de direction par rapport à l'$x$axe positif.

Cette image est la vue latérale d'une automobile. À l'avant de l'automobile, il y a un vecteur horizontal étiqueté « 300 livres ». De plus, à l'avant de l'automobile, il y a un autre vecteur étiqueté « 150 livres ». L'angle entre les deux vecteurs est de 15 degrés. — Figure$\PageIndex{20}$ : Deux forces agissant sur une voiture dans des directions différentes.

Solution

Pour déterminer l'effet de la combinaison des deux forces, ajoutez leurs vecteurs représentatifs. Tout d'abord, exprimez chaque vecteur sous forme de composant ou en termes de vecteurs unitaires standard. Pour ce faire, il est plus facile d'aligner l'un des vecteurs sur l'$x$axe positif. Le vecteur horizontal possède donc un point initial$(0,0)$ et un point terminal$(300,0)$. Il peut être exprimé sous la forme$⟨300,0⟩$ ou$300 \hat{\mathbf i}$.

Le second vecteur a une amplitude$150$ et fait un angle de$15°$ avec le premier, donc nous pouvons l'exprimer sous la forme$⟨150 \cos(15°),150 \sin(15°)⟩,$ ou$150 \cos(15°)\hat{\mathbf i}+150 \sin(15°)\hat{\mathbf j}$. Ensuite, la somme des vecteurs, ou vecteur résultant, est$\vecs{r}=⟨300,0⟩+⟨150 \cos(15°),150 \sin(15°)⟩,$ et nous avons

\[\|\vecs{r}\|=\sqrt{(300+150 \cos(15°))^2+(150 \sin(15°))^2}≈446.6. \nonumber \]

L'angle$θ$ formé par$\vecs{r}$ et l'$x$axe positif a donc$\tan θ=\dfrac{150 \sin 15°}{(300+150\cos 15°)}≈0.09$$θ≈ \tan^{−1}(0.09)≈5°$, ce qui signifie que la force résultante$\vecs{r}$ a un angle$5°$ supérieur à l'axe horizontal.

Exemple$\PageIndex{9B}$: Finding Resultant Velocity

Un avion vole plein ouest à une vitesse anémométrique de$425$ mi/h. Le vent souffle du nord-est à$40$ mph. Quelle est la vitesse au sol de l'avion ? Quel est le cap de l'avion ?

Solution

Commençons par esquisser la situation décrite (Figure$\PageIndex{21}$).

Cette figure est l'image d'un avion. Deux vecteurs sortent de l'avant de l'avion. Le premier vecteur est étiqueté « 425 » et le second vecteur est étiqueté « 40 ». L'angle entre les vecteurs est de 45 degrés. — Figure$\PageIndex{21}$ : Dans un premier temps, l'avion se déplace plein ouest. Le vent vient du nord-est, il souffle donc vers le sud-ouest. L'angle entre la trajectoire de l'avion et le vent est de$45°$. (Figure non dessinée à l'échelle.)

Établissez une esquisse de manière à ce que les points initiaux des vecteurs se situent à l'origine. Ensuite, le vecteur de vitesse de l'avion est$\vecs{p}=−425\hat{\mathbf i}$. Le vecteur décrivant le vent fait un angle de$225°$ avec l'$x$axe positif :

\[\vecs{w}=⟨40 \cos(225°),40 \sin(225°)⟩=⟨−\dfrac{40}{\sqrt{2}},−\dfrac{40}{\sqrt{2}}⟩=−\dfrac{40}{\sqrt{2}}\hat{\mathbf i}−\dfrac{40}{\sqrt{2}}\hat{\mathbf j}. \nonumber \]

Lorsque la vitesse et le vent agissent ensemble sur l'avion, nous pouvons ajouter leurs vecteurs pour trouver la force résultante :

\[\vecs{p}+\vecs{w}=−425\hat{\mathbf i}+(−\dfrac{40}{\sqrt{2}}\hat{\mathbf i}−\dfrac{40}{\sqrt{2}}\hat{\mathbf j})=(−425−\dfrac{40}{\sqrt{2}})\hat{\mathbf i}−\dfrac{40}{\sqrt{2}}\hat{\mathbf j}. \nonumber \]

L'amplitude du vecteur résultant montre l'effet du vent sur la vitesse au sol de l'avion :

$\|\vecs{p}+\vecs{w}\|=\sqrt{(−425−\dfrac{40}{\sqrt{2}})^2+(−\dfrac{40}{\sqrt{2}})^2}≈454.17$mi/h

En raison du vent, l'avion se déplace à environ$454$ mi/h par rapport au sol.

Pour déterminer le cap de l'avion, nous voulons trouver la direction du vecteur$\vecs{p}+\vecs{w}$ :

$\tan θ=\dfrac{−\dfrac{40}{\sqrt{2}}}{(−425−\dfrac{40}{\sqrt{2}})}≈0.06$

$θ≈3.57°$.

La direction générale de l'avion se$3.57°$ situe au sud-ouest.

Exercice$\PageIndex{9}$

Un avion vole plein nord à une vitesse anémométrique de$550$ mi/h. Le vent souffle du nord-ouest à$50$ mph. Quelle est la vitesse au sol de l'avion ?

Allusion: Esquissez les vecteurs avec le même point initial et trouvez leur somme.
Réponse: Environ$516$ mi/h

Concepts clés

Les vecteurs sont utilisés pour représenter des quantités qui ont à la fois une amplitude et une direction.
Nous pouvons ajouter des vecteurs en utilisant la méthode du parallélogramme ou la méthode du triangle pour trouver la somme. On peut multiplier un vecteur par un scalaire pour modifier sa longueur ou lui donner la direction opposée.
La soustraction de vecteurs est définie en termes d'addition du négatif du vecteur.
Un vecteur est écrit sous forme de composant sous la forme$\vecs{v}=⟨x,y⟩$.
La magnitude d'un vecteur est scalaire :$‖\vecs{v}‖=\sqrt{x^2+y^2}$.
Un vecteur unitaire$\vecs{u}$ a une amplitude$1$ et peut être trouvé en divisant un vecteur par sa magnitude :$\vecs{u}=\dfrac{1}{‖\vecs{v}‖}\vecs{v}$. Les vecteurs unitaires standard sont$\hat{\mathbf i}=⟨1,0⟩$ et$\hat{\mathbf j}=⟨0,1⟩$. Un vecteur$\vecs{v}=⟨x,y⟩$ peut être exprimé en termes de vecteurs unitaires standard sous la forme$\vecs{v}=x\hat{\mathbf i}+y\hat{\mathbf j}$.
Les vecteurs sont souvent utilisés en physique et en ingénierie pour représenter des forces et des vitesses, entre autres grandeurs.

Lexique

composant: un scalaire qui décrit la direction verticale ou horizontale d'un vecteur

vecteurs équivalents: vecteurs ayant la même magnitude et la même direction

point initial: le point de départ d'un vecteur

magnitude: la longueur d'un vecteur

normalisation: utilisation de la multiplication scalaire pour trouver un vecteur unitaire avec une direction donnée

méthode du parallélogramme: une méthode pour trouver la somme de deux vecteurs ; positionner les vecteurs de manière à ce qu'ils partagent le même point initial ; les vecteurs forment ensuite deux côtés adjacents d'un parallélogramme ; la somme des vecteurs est la diagonale de ce parallélogramme

scalaire: un vrai nombre

multiplication scalaire: une opération vectorielle qui définit le produit d'un scalaire et d'un vecteur

vecteur de position standard: un vecteur avec point initial$(0,0)$

vecteurs unitaires standard: vecteurs unitaires le long des axes de coordonnées :$\hat{\mathbf i}=⟨1,0⟩,\, \hat{\mathbf j}=⟨0,1⟩$

point terminal: le point final d'un vecteur

inégalité triangulaire: la longueur de n'importe quel côté d'un triangle est inférieure à la somme des longueurs des deux autres côtés

méthode triangulaire: une méthode pour trouver la somme de deux vecteurs ; positionner les vecteurs de telle sorte que le point terminal d'un vecteur soit le point initial de l'autre ; ces vecteurs forment alors les deux côtés d'un triangle ; la somme des vecteurs est le vecteur qui forme le troisième côté ; le point initial de la somme est le point initial du premier vecteur ; le point terminal de la somme est le point terminal du second vecteur

vecteur unitaire: un vecteur avec une magnitude$1$

vecteur: un objet mathématique qui possède à la fois une amplitude et une direction

ajout de vecteurs: une opération vectorielle qui définit la somme de deux vecteurs

différence vectorielle: la différence vectorielle$\vecs{v}−\vecs{w}$ est définie comme$\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}$

somme vectorielle: la somme de deux vecteurs,$\vecs{v}$ et$\vecs{w}$, peut être construite graphiquement en plaçant le point initial de$\vecs{w}$ au point terminal de$\vecs{v}$ ; alors la somme vectorielle$\vecs{v}+\vecs{w}$ est le vecteur dont le point initial coïncide avec le point initial de$\vecs{v}$, et avec un point terminal qui coïncide avec le point terminal de$\vecs{w}$

vecteur zéro: le vecteur avec à la fois le point initial et le point terminal$(0,0)$

Définition : Vecteurs équivalents

Exemple\(\PageIndex{1}\): Sketching Vectors

Exercice\(\PageIndex{1}\)

Définition : Multiplication scalaire

Définition : Addition de vecteurs

Exemple\(\PageIndex{2}\): Combining Vectors

Exercice\(\PageIndex{2}\)

Exemple\(\PageIndex{3}\): Comparing Vectors

Exercice\(\PageIndex{3}\)

Définition : composants vectoriels

Règle : Forme constitutive d'un vecteur

Exemple\(\PageIndex{4}\): Expressing Vectors in Component Form

Exercice\(\PageIndex{4}\)

Définition : Multiplication scalaire et addition de vecteurs

Exemple\(\PageIndex{5}\): Performing Operations in Component Form

Exercice\(\PageIndex{5A}\)

Propriétés des opérations vectorielles

Preuve de propriété commutative

Preuve de propriété distributive

Exercice\(\PageIndex{5B}\)

Exemple\(\PageIndex{6}\): Finding the Component Form of a Vector Using Trigonometry

Exercice\(\PageIndex{6}\)

Exemple\(\PageIndex{7}\): Finding a Unit Vector

Exercice\(\PageIndex{7}\)

Exemple\(\PageIndex{8}\): Using Standard Unit Vectors

Exercice\(\PageIndex{8}\)

Exemple\(\PageIndex{9A}\): Finding Resultant Force

Exemple\(\PageIndex{9B}\): Finding Resultant Velocity

Exercice\(\PageIndex{9}\)