7.7 : Intégrales incorrectes

Objectifs d'apprentissage

• Evaluez une intégrale sur un intervalle infini.
• Evaluez une intégrale sur un intervalle fermé avec une discontinuité infinie au sein de l'intervalle.
• Utilisez le théorème de comparaison pour déterminer si une intégrale définie est convergente.

L'aire entre le graphe de\(f(x)=\dfrac{1}{x}\) et l'\(x\)axe -sur l'intervalle est-elle\([1,+∞)\) finie ou infinie ? Si cette même région tourne autour de l'\(x\)axe -, le volume est-il fini ou infini ? Étonnamment, l'aire de la région décrite est infinie, mais le volume du solide obtenu en faisant tourner cette région autour de l'\(x\)axe y est fini.

Dans cette section, nous définissons des intégrales sur un intervalle infini ainsi que des intégrales de fonctions contenant une discontinuité sur l'intervalle. Les intégrales de ces types sont appelées intégrales incorrectes. Nous examinons plusieurs techniques pour évaluer les intégrales incorrectes, qui impliquent toutes de prendre des limites.

Intégration sur un intervalle infini

Comment devons-nous définir une intégrale du type\(\displaystyle \int ^{+∞}_af(x)\,dx?\) que nous pouvons intégrer\(\displaystyle \int ^t_af(x)\,dx\) pour n'importe quelle valeur de\(t\), il est donc raisonnable d'examiner le comportement de cette intégrale lorsque nous substituons des valeurs plus grandes de\(t\). La figure\(\PageIndex{1}\) montre que cela\(\displaystyle \int ^t_af(x)\,dx\) peut être interprété comme une aire pour différentes valeurs de\(t\). En d'autres termes, nous pouvons définir une intégrale impropre comme une limite, considérée comme l'une des limites de l'intégration augmente ou diminue sans limite.

Figure\(\PageIndex{1}\) : Pour intégrer une fonction sur un intervalle infini, nous considérons la limite de l'intégrale lorsque la limite supérieure augmente sans limite.

Définition : intégrale incorrecte

1. Laissez\(f(x)\) agir en continu sur un intervalle du formulaire\([a,+∞)\). Ensuite,\[\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx, \label{improper1} \] à condition que cette limite existe.
2. Laissez\(f(x)\) agir en continu sur un intervalle du formulaire\((−∞,b]\). Ensuite,\[\int ^b_{−∞}f(x)\,dx=\lim_{t→−∞}\int ^b_tf(x)\,dx, \label{improper2} \] à condition que cette limite existe.

Dans chaque cas, si la limite existe, on dit que l'intégrale incorrecte converge. Si la limite n'existe pas, on dit que l'intégrale incorrecte diverge.

3. \(f(x)\)Soyons continus\((−∞,+∞)\). Ensuite,\[\int ^{+∞}_{−∞}f(x)\,dx=\int ^0_{−∞}f(x)\,dx+\int ^{+∞}_0f(x)\,dx, \label{improper3} \] à condition que\(\displaystyle \int ^0_{−∞}f(x)\,dx\) les\(\displaystyle \int ^{+∞}_0f(x)\,dx\) deux convergent. Si l'une de ces deux intégrales diverge, alors\(\displaystyle \int ^{+∞}_{−∞}f(x)\,dx\) diverge. (Il peut être démontré que, en fait,\(\displaystyle \int ^{+∞}_{−∞}f(x)\,dx=\int ^a_{−∞}f(x)\,dx+\int ^{+∞}_af(x)\,dx\) pour n'importe quelle valeur de a.).

Dans notre premier exemple, nous revenons à la question que nous avons posée au début de cette section : L'aire entre le graphe de\(f(x)=\frac{1}{x}\) et l'\(x\)axe -sur l'intervalle est-elle\([1,+∞)\) finie ou infinie ?

Exemple\(\PageIndex{1}\): Finding an Area

Déterminez si l'aire entre le graphe de\(f(x)=\dfrac{1}{x}\) et l'\(x\)axe -sur l'intervalle\([1,+∞)\) est finie ou infinie.

Solution

Nous faisons d'abord une esquisse rapide de la région en question, comme le montre la figure\(\PageIndex{2}\).

Figure\(\PageIndex{2}\) : Nous pouvons trouver l'aire entre la courbe\(f(x)=1/x\) et l'\(x\)axe -sur un intervalle infini.

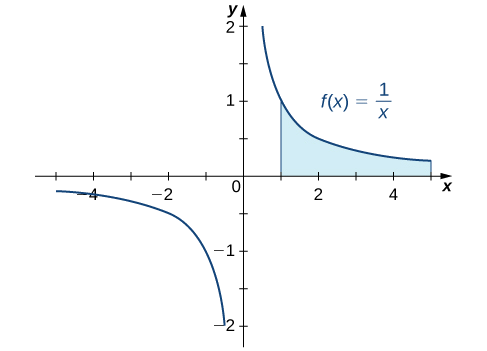
Nous pouvons voir que la superficie de cette région est donnée par

\[A=\int ^∞_1\frac{1}{x}\,dx. \nonumber \]

qui peut être évaluée à l'aide de l'équation \ ref {improper1} :

\[ \begin{align*} A =\int ^∞_1\frac{1}{x}\,dx \nonumber \\[4pt] =\lim_{t→+∞}\int ^t_1\frac{1}{x}\,dx \tag{Rewrite the improper integral as a limit} \\[4pt] =\lim_{t→+∞}\ln |x|∣^t_1 \tag{Find the antiderivative} \\[4pt] =\lim_{t→+∞}(\ln |t|−\ln 1) \tag{Evaluate the antiderivative} \\[4pt] =+∞. \tag{Evaluate the limit.} \end{align*} \]

Puisque l'intégrale impropre diverge,\(+∞,\) la zone de la région est infinie.

Exemple\(\PageIndex{2}\): Finding a Volume

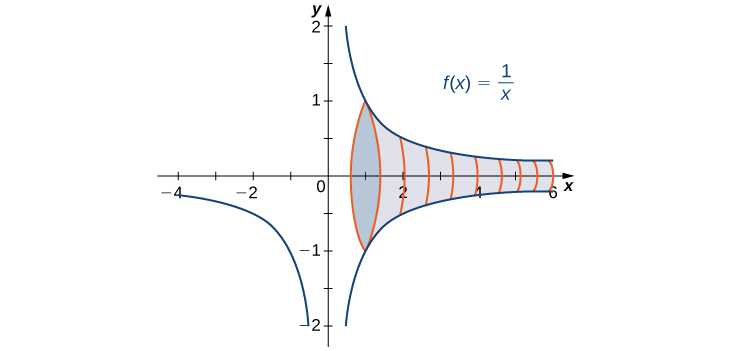
Déterminez le volume du solide obtenu en faisant tourner la région délimitée par le graphique\(f(x)=\dfrac{1}{x}\) et l'\(x\)axe -sur l'intervalle\([1,+∞)\) autour de l'\(x\)axe.

Solution

Le solide est illustré sur la figure\(\PageIndex{3}\). En utilisant la méthode du disque, nous voyons que le volume\(V\) est

\[V=π\int ^{+∞}_1\frac{1}{x^2}\,dx. \nonumber \]

Figure\(\PageIndex{3}\) : Le solide de révolution peut être généré en faisant pivoter une zone infinie autour de\(x\) l'axe.

Ensuite, nous avons

\ [\ displaystyle \ begin {align*} V &=π \ int ^ {+∞} _1 \ frac {1} {x^2} \, dx \ \ [4pt]
&=π \ lim_ {t→+∞} \ int ^t_1 \ frac {1} {x^2} \, dx \ quad \ text {Réécrire comme limite.} \ \ [4pt]
&=π \ lim_ {t→+∞} − \ frac {1} {x} ^t_1 \ quad \ text {Trouvez l'antidérivé.} \ \ [4pt]
&=π \ lim_ {t→+∞} \ left (− \ frac {1} {t} +1 \ right) \ quad \ text {Évaluez l'antidérivé.} \ \ [4pt]
&=π \ end {align*} \]

L'intégrale incorrecte converge vers\(π\). Par conséquent, le volume du solide de révolution est\(π\).

En conclusion, bien que l'aire de la région située entre l'\(x\)axe -et le graphe de l'\(f(x)=1/x\)intervalle\([1,+∞)\) soit infinie, le volume du solide généré par la rotation de cette région autour de l'\(x\)axe -est fini. Le solide généré est connu sous le nom de corne de Gabriel.

Remarque : Le cor de Gabriel (également appelé trompette de Torricelli) est une figure géométrique qui a une surface infinie, mais un volume limité. Le nom fait référence à la tradition identifiant l'archange Gabriel comme étant l'ange qui sonne la corne pour annoncer le Jugement dernier, associant le divin, ou l'infini, au fini. Les propriétés de cette figure ont été étudiées pour la première fois par le physicien et mathématicien italien Evangelista Torricelli au XVIIe siècle.

Exemple\(\PageIndex{3}\): Traffic Accidents in a City

Supposons qu'à une intersection très fréquentée, les accidents de la circulation se produisent en moyenne un tous les trois mois. À la suite de plaintes de résidents, des modifications ont été apportées aux feux de circulation à l'intersection. Cela fait maintenant huit mois que les modifications ont été apportées et il n'y a eu aucun accident. Les modifications ont-elles été efficaces ou l'intervalle de 8 mois sans accident est-il le résultat du hasard ?

Figure\(\PageIndex{4}\) : Modification de l'œuvre de David McKelvey, Flickr.

La théorie des probabilités nous dit que si le temps moyen entre les événements est\(k\), la probabilité que\(X\), le temps entre les événements, se situe entre\(a\) et\(b\) est donnée par

\[(P(a≤x≤b)=\int ^b_af(x)\,dx \nonumber \]

où

\[f(x)=\begin{cases}0, \text{if}\;x<0\\ke^{−kx}, \text{if}\;x≥0\end{cases}. \nonumber \]

Ainsi, si un accident se produit à raison d'un accident tous les trois mois, alors la probabilité que\(X\), entre les accidents, se situe entre\(a\) et\(b\) est donnée par

\[P(a≤x≤b)=\int ^b_af(x)\,dx \nonumber \]

où\[f(x)=\begin{cases}0, \text{if}\;x<0\\3e^{−3x}, \text{if}\;x≥0\end{cases}. \nonumber \]

Pour répondre à la question, nous devons calculer\(\displaystyle P(X≥8)=\int ^{+∞}_83e^{−3x}\,dx\) et décider s'il est probable que 8 mois se seraient écoulés sans accident s'il n'y avait pas eu d'amélioration de la situation de la circulation.

Solution

Nous devons calculer la probabilité sous la forme d'une intégrale incorrecte :

\ (\ displaystyle \ begin {align*} P (X≥8) = \ int ^ {+∞} _83e^ {−3x} \, dx \ \ [4 points]
= \ lim_ {t→+∞} \ int ^t_83e^ {−3x} \, dx \ \ [4 points]
= \ lim_ {t→+∞} −e^ {−3x} ^t_8 \ \ [4 points]
= \ lim_ {t→+∞} (−e^ {−3t} +e^ {−24}) \ \ [4 points]
≈ 3,8 × 10^ {−11}. \ end {align*} \)

La valeur\(3.8×10^{−11}\) représente la probabilité qu'aucun accident ne survienne en 8 mois dans les conditions initiales. Comme cette valeur est très, très faible, il est raisonnable de conclure que les modifications ont été efficaces.

Exemple\(\PageIndex{4}\): Evaluating an Improper Integral over an Infinite Interval

\(\displaystyle \int ^0_{−∞}\frac{1}{x^2+4}\,dx.\)Évaluez si l'intégrale incorrecte converge ou diverge.

Solution

Commencez par réécrire\(\displaystyle \int ^0_{−∞}\frac{1}{x^2+4}\,dx\) une limite à l'aide de l'équation \ ref {improper2} de la définition. Ainsi,

\ [\ begin {align*} \ int ^0_ {−∞} \ frac {1} {x^2+4} \, dx &= \ lim_ {t→−∞} \ int ^0_t \ frac {1} {x^2+4} \, dx \ quad \ text {Réécrire sous forme de limite.} \ \ [4pt]
&= \ lim_ {t−→t−−4} ∞} \ frac {1} {2} \ tan^ {−1} \ frac {x} {2} ^0_t \ quad \ text {Trouvez l'antidérivé.} \ \ [4pt]
&= \ lim_ {t→−∞} \ left (\ frac {1} {2} \ tan^ {−1} 0− \ frac {1} {2} \ tan^ {−1} \ frac {t} {2} \ right) \ quad \ text {Évaluez l'antidérivé.} \ \ [4pt]
&= \ frac {π} {4}. \ quad \ text {Évaluez la limite et simplifiez-la.} \ end {align*} \]

L'intégrale incorrecte converge vers\(\dfrac{π}{4}.\)

Exemple\(\PageIndex{5}\): Evaluating an Improper Integral on \((−∞,+∞)\)

\(\displaystyle \int ^{+∞}_{−∞}xe^x\,dx.\)Évaluez si l'intégrale incorrecte converge ou diverge.

Solution

Commencez par diviser l'intégrale :

\[\int ^{+∞}_{−∞}xe^x\,dx=\int ^0_{−∞}xe^x\,dx+\int ^{+∞}_0xe^x\,dx. \nonumber \]

Si l'un\(\displaystyle \int ^0_{−∞}xe^x\,dx\) ou l'autre\(\displaystyle \int ^{+∞}_0xe^x\,dx\) diverge, alors\(\displaystyle \int ^{+∞}_{−∞}xe^x\,dx\) diverge. Calculez chaque intégrale séparément. Pour la première intégrale,

\(\displaystyle \int ^0_{−∞}xe^x\,dx=\lim_{t→−∞}\int ^0_txe^x\,dx\)Réécrivez comme limite.

\(=\lim_{t→−∞}(xe^x−e^x)∣^0_t\)Utilisez l'intégration par parties pour trouver l'antidérivé. (Ici\(u=x\) et\(dv=e^x\).)

\(=\lim_{t→−∞}(−1−te^t+e^t)\)Évaluez l'antidérivé.

\(=−1.\)

Évaluez la limite. Remarque :\(\displaystyle \lim_{t→−∞}te^t\) est indéterminé de forme\(0⋅∞\). Ainsi,\(\displaystyle \lim_{t→−∞}te^t=\lim_{t→−∞}\frac{t}{e^{−t}}=\lim_{t→−∞}\frac{−1}{e^{−t}}=\lim_{t→−∞}−e^t=0\) selon la règle de L'Hôpital.

La première intégrale impropre converge. Pour la deuxième intégrale,

\(\displaystyle \int ^{+∞}_0xe^x\,dx=\lim_{t→+∞}\int ^t_0xe^x\,dx\)Réécrivez comme limite.

\(=\lim_{t→+∞}(xe^x−e^x)∣^t_0\)Trouvez l'antidérivé.

\(=\lim_{t→+∞}(te^t−e^t+1)\)Évaluez l'antidérivé.

\(=\lim_{t→+∞}((t−1)e^t+1)\)Réécrire. (\(te^t−e^t\)est indéterminé.)

\(=+∞.\)Évaluez la limite.

Ainsi,\(\displaystyle \int ^{+∞}_0xe^x\,dx\) diverge. Puisque cette intégrale diverge, elle\(\displaystyle \int ^{+∞}_{−∞}xe^x\,dx\) diverge également.

Exercice\(\PageIndex{1}\)

\(\displaystyle \int ^{+∞}_{−3}e^{−x}\,dx.\)Évaluez si l'intégrale incorrecte converge ou diverge.

Allusion

\[\int ^{+∞}_{−3}e^{−x}\,dx=\lim_{t→+∞}\int ^t_{−3}e^{−x}\,dx \nonumber \]

Réponse

Il converge vers\(e^3.\)

Intégrer un Integrand discontinu

Examinons maintenant les intégrales de fonctions contenant une discontinuité infinie dans l'intervalle au cours duquel l'intégration se produit. Considérez une intégrale de la forme\(\displaystyle \int ^b_af(x)\,dx,\) où\(f(x)\) est continue\([a,b)\) et discontinue à\(b\). Puisque la fonction\(f(x)\) est continue\([a,t]\) pour toutes les valeurs de\(t\) satisfaction\(a \le t<b\), l'intégrale\(\displaystyle \int ^t_af(x)\,dx\) est définie pour toutes ces valeurs de\(t\). Il est donc logique de considérer les valeurs de\(\displaystyle \int ^t_af(x)\,dx\) en tant qu'\(t\)approches\(b\) pour\(a \le t<b\). C'est-à-dire, nous définissons\(\displaystyle \int ^b_af(x)\,dx=\lim_{t→b^−}\int ^t_af(x)\,dx\), à condition que cette limite existe. La figure\(\PageIndex{5}\) illustre\(\displaystyle \int ^t_af(x)\,dx\) sous forme de zones de régions pour les valeurs d'\(t\)approche\(b\).

Figure\(\PageIndex{5}\) : Lorsque t s'approche de b par la gauche, la valeur de l'aire de a à t se rapproche de la zone de a à b.

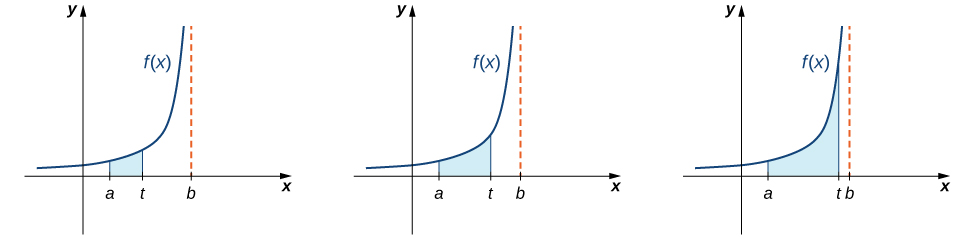
Nous utilisons une approche similaire pour définir\(\displaystyle \int ^b_af(x)\,dx\) où\(f(x)\) est continu\((a,b]\) et discontinu à\(a\). Nous procédons maintenant à une définition formelle.

Définition : Intégrale incorrecte convergente et divergente

1. \(f(x)\)Soyons continus\([a,b)\). Ensuite,\[\int ^b_af(x)\,dx=\lim_{t→b^−}\int ^t_af(x)\,dx. \label{improperundefb} \]
2. \(f(x)\)Soyons continus\((a,b]\). Ensuite,\[\int ^b_af(x)\,dx=\lim_{t→a^+}\int ^b_tf(x)\,dx. \label{improperundefa} \] dans chaque cas, si la limite existe, on dit que l'intégrale incorrecte converge. Si la limite n'existe pas, on dit que l'intégrale incorrecte diverge.
3. Il\(f(x)\) est continu\([a,b]\) sauf à un point d'entrée\(c\)\((a,b)\), puis\[\int ^b_af(x)\,dx=\int ^c_af(x)\,dx+\int ^b_cf(x)\,dx,\label{improperundefc} \] fournit les deux\(\displaystyle \int ^c_af(x)\,dx\) et\(\displaystyle \int ^b_cf(x)\,dx\) converge. Si l'une de ces intégrales diverge, alors\(\displaystyle \int ^b_af(x)\,dx\) diverge.

Les exemples suivants illustrent l'application de cette définition.

Exemple\(\PageIndex{6}\): Integrating a Discontinuous Integrand

Évaluez\(\displaystyle \int ^4_0\frac{1}{\sqrt{4−x}}\,dx,\) si possible. Indiquez si l'intégrale converge ou diverge.

Solution

La fonction\(f(x)=\dfrac{1}{\sqrt{4−x}}\) est continue\([0,4)\) et discontinue à 4. En utilisant l'équation \ ref {improperundefb} de la définition, réécrivez\(\displaystyle \int ^4_0\frac{1}{\sqrt{4−x}}\,dx\) comme limite :

\ (\ displaystyle \ begin {align*} \ int ^4_0 \ frac {1} {\ sqrt {4−x}} \, dx &= \ lim_ {t→4^−} \ int ^t_0 \ frac {1} {\ sqrt {4−x}} \, dx \ quad \ text {Réécrire comme limite.} \ \ [4pt]
&= \ \ lim_ {t→4^−} (−2 \ sqrt {4−x}) ^t_0 \ quad \ text {Trouvez l'antidérivé.} \ \ [4pt]
&= \ lim_ {t→4^−} (−2 \ sqrt {4−t} +4) \ quad \ text {Évaluez l'antidérivé.} \ \ [4pt]
&=4. \ quad \ text {Évaluez la limite.} \ end {align*} \)

L'intégrale impropre converge.

Exemple\(\PageIndex{7}\): Integrating a Discontinuous Integrand

Évaluez\(\displaystyle \int ^2_0x\ln x\,dx.\) l'État si l'intégrale converge ou diverge.

Solution

Comme elle\(f(x)=x\ln x\) est continue\((0,2]\) et discontinue à zéro, nous pouvons réécrire l'intégrale sous forme limite en utilisant l'équation \ ref {improperundefa} :

\ (\ displaystyle \ begin {align*} \ int ^2_0x \ ln x \, dx &= \ lim_ {t→0^+} \ int ^2_tx \ ln x \, dx \ quad \ text {Réécrivez comme limite.} \ \ [4pt]
&= \ lim_ {t→0^+} (\ frac {1} {2} x^2 \ ln x− \ frac {1} {4} x^2) ^2_t \ quad \ text {Évaluer} \ ; \ int x \ ln x \, dx \ ; \ text {en utilisant l'intégration par parties avec} \ ; u= \ ln x \ ; \ text {et} \ ; dv=x. \ \ [4 points]
&= \ lim_ {t→0^+} (2 \ ln 2−1− \ frac {1} {2} t^2 \ ln t+ \ frac {1} {4} t^2). \ quad \ text {Évaluez l'antidérivé.} \ \ [4pt]
&=2 \ ln 2−1. \ quad \ text {Évaluez la limite.} \ end {align*} \)

Donc

\(\displaystyle \lim_{t→0^+}t^2\ln t\;\text{is indeterminate.}\)

Pour l'évaluer, réécrivez-le sous forme de quotient et appliquez la règle de L'Hôpital.

L'intégrale impropre converge.

Exemple\(\PageIndex{8}\): Integrating a Discontinuous Integrand

\(\displaystyle \int ^1_{−1}\frac{1}{x^3}\,dx.\)Évaluez si l'intégrale incorrecte converge ou diverge.

Solution

Puisque\(f(x)=1/x^3\) est discontinu à zéro, en utilisant l'équation \ ref {improperundefc}, nous pouvons écrire

\[\int ^1_{−1}\frac{1}{x^3}\,dx=\int ^0_{−1}\frac{1}{x^3}\,dx+\int ^1_0\frac{1}{x^3}\,dx.\nonumber \]

Si l'une des deux intégrales diverge, alors l'intégrale d'origine diverge. Commencez par\(\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx\) :

\(\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx=\lim_{t→0^−}\int ^t_{−1}\frac{1}{x^3}\,dx\)Réécrivez comme limite.

\(=\lim_{t→0^−}(−\frac{1}{2x^2})∣^t_{−1}\)Trouvez l'antidérivé.

\(=\lim_{t→0^−}(−\frac{1}{2t^2}+\frac{1}{2})\)Évaluez l'antidérivé.

\(=+∞.\)Évaluez la limite.

Par conséquent,\(\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx\) diverge. Puisque\(\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx\) diverge,\(\displaystyle \int ^1_{−1}\frac{1}{x^3}\,dx\) diverge.

Exercice\(\PageIndex{2}\)

Évaluez\(\displaystyle \int ^2_0\frac{1}{x}\,dx.\) l'État si l'intégrale converge ou diverge.

Allusion

Écrivez\(\displaystyle \int ^2_0\frac{1}{x}\,dx\) sous forme de limite en utilisant l'équation \ ref {improperundefa}.

Réponse

\(+∞\), Elle diverge.

Un théorème de comparaison

Il n'est pas toujours facile ni même possible d'évaluer directement une intégrale incorrecte ; toutefois, en la comparant à une autre intégrale soigneusement choisie, il peut être possible de déterminer sa convergence ou sa divergence. Pour voir cela, considérez deux fonctions continues\(f(x)\) et\(g(x)\) satisfaisantes\(0≤f(x)≤g(x)\) pour\(x≥a\) (Figure\(\PageIndex{6}\)). Dans ce cas, nous pouvons considérer les intégrales de ces fonctions sur des intervalles du formulaire\([a,t]\) comme des zones, nous avons donc la relation

\[ 0≤\int ^t_af(x)\,dx≤\int ^t_ag(x)\,dx \nonumber \]

pour\(t≥a\).

Figure\(\PageIndex{6}\) : Si\(0≤f(x)≤g(x)\) pour\(x≥a\), alors pour\(t≥a\),\(\displaystyle \int ^t_af(x)\,dx≤\int ^t_ag(x)\,dx.\)

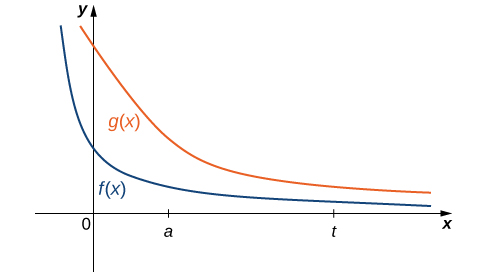
Ainsi, si

\[\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=+∞, \nonumber \]

alors

\[\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=+∞ \nonumber \]

aussi. En d'autres termes, si l'aire de la région située entre le graphe de\(f(x)\) et l'\(x\)axe -over\([a,+∞)\) est infinie, alors l'aire de la région située entre le graphe de\(g(x)\) et l'\(x\)axe -over\([a,+∞)\) est également infinie.

D'un autre côté, si

\[\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=L \nonumber \]

pour un nombre réel\(L\), alors

\[\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx \nonumber \]

doit converger vers une valeur inférieure ou égale à\(L\), car\(\displaystyle \int ^t_af(x)\,dx\) augmente au fur et à\(t\) mesure et\(\displaystyle \int ^t_af(x)\,dx≤L\) pour tous\(t≥a.\)

Si l'aire de la région située entre le graphe de\(g(x)\) et l'\(x\)axe -over\([a,+∞)\) est finie, alors l'aire de la région située entre le graphe de\(f(x)\) et l'\(x\)axe -over\([a,+∞)\) est également finie.

Ces conclusions sont résumées dans le théorème suivant.

Un théorème de comparaison

Laissons\(f(x)\) et\(g(x)\) soyez continus sur\([a,+∞).\) Supposons que\(0≤f(x)≤g(x)\) pour\(x≥a.\)

1. Si\[\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=+∞, \nonumber \] alors\[\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=+∞. \nonumber \]
2. Si\[\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=L, \nonumber \] où\(L\) est un vrai nombre, alors\[\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=M \nonumber \] pour un nombre réel\(M≤L.\)

Exemple\(\PageIndex{9}\): Applying the Comparison Theorem

Utilisez une comparaison pour montrer que

\[\int ^{+∞}_1\frac{1}{xe^x}\,dx \nonumber \]

converge.

Solution

Nous pouvons voir que

\[0≤\frac{1}{xe^x}≤\frac{1}{e^x}=e^{−x}, \nonumber \]

donc si elle\(\displaystyle \int ^{+∞}_1e^{−x}\,dx\) converge, il en va de même\(\displaystyle \int ^{+∞}_1\frac{1}{xe^x}\,dx\). Pour évaluer,\(\displaystyle \int ^{+∞}_1e^{−x}\,dx,\) commencez par la réécrire en tant que limite :

\(\displaystyle \int ^{+∞}_1e^{−x}\,dx=\lim_{t→+∞}\int ^t_1e^{−x}\,dx\)

\(=\lim_{t→+∞}(−e^{−x})∣^t_1\)

\(=\lim_{t→+∞}(−e^{−t}+e^{-1})\)

\(=e^{-1}.\)

Puisque\(\displaystyle \int ^{+∞}_1e^{−x}\,dx\) converge, il en va de même\(\displaystyle \int ^{+∞}_1\frac{1}{xe^x}\,dx.\)

Exemple\(\PageIndex{10}\): Applying the Comparison Theorem

Utilisez le théorème de comparaison pour montrer que cela\(\displaystyle \int ^{+∞}_1\frac{1}{x^p}\,dx\) diverge pour tous\(p<1\).

Solution

Pour\(p<1, 1/x≤1/(x^p)\) plus de\([1,+∞).\) In Example\(\PageIndex{1}\), nous avons montré que\(\displaystyle \int ^{+∞}_1\frac{1}{x}\,dx=+∞.\) Donc,\(\displaystyle \int ^{+∞}_1\frac{1}{x^p}\,dx\) diverge pour tous\(p<1\).

Exercice\(\PageIndex{3}\)

Utilisez une comparaison pour montrer qu'il\(\displaystyle \int ^{+∞}_e\frac{\ln x}{x}\,dx\) y a divergence.

Allusion

\(\frac{1}{x}≤\frac{\ln x}{x}\)sur\([e,+∞)\)

Réponse

Depuis\(\displaystyle \int ^{+∞}_e\frac{1}{x}\,dx=+∞,\)\(\displaystyle \int ^{+∞}_e\frac{\ln x}{x}\,dx\) diverge.

Les transformations de Laplace

Dans les derniers chapitres, nous avons examiné plusieurs manières d'utiliser l'intégration pour résoudre des problèmes du monde réel. Pour ce prochain projet, nous allons explorer une application plus avancée de l'intégration : les transformations intégrales. Plus précisément, nous décrivons la transformée de Laplace et certaines de ses propriétés. La transformée de Laplace est utilisée en ingénierie et en physique pour simplifier les calculs nécessaires à la résolution de certains problèmes. Il prend des fonctions exprimées en termes de temps et les transforme en fonctions exprimées en termes de fréquence. Il s'avère que, dans de nombreux cas, les calculs nécessaires pour résoudre les problèmes dans le domaine des fréquences sont beaucoup plus simples que ceux requis dans le domaine temporel.

La transformée de Laplace est définie en termes d'intégrale comme

\[L{f(t)}=F(s)=\int ^∞_0e^{−st}f(t)dt. \nonumber \]

Notez que l'entrée d'une transformée de Laplace est fonction du temps\(f(t),\) et que la sortie est fonction de la fréquence\(F(s)\). Bien que de nombreux exemples du monde réel nécessitent l'utilisation de nombres complexes (impliquant le nombre imaginaire),\(i=\sqrt{−1}),\) dans ce projet, nous nous limitons aux fonctions des nombres réels.

Commençons par un exemple simple. Nous calculons ici la transformée de Laplace de\(f(t)=t\). Nous avons

\[L{t}=\int ^∞_0te^{−st}dt. \nonumber \]

Il s'agit d'une intégrale inappropriée, nous l'exprimons donc en termes de limite, ce qui donne

\[L{t}=\int ^∞_0te^{−st}dt=\lim_{z→∞}\int ^z_0te^{−st}dt. \nonumber \]

Nous utilisons maintenant l'intégration par parties pour évaluer l'intégrale. Notez que nous intégrons par rapport à t, donc nous traitons la variable s comme une constante. Nous avons

\(u=t\)\(du=dt\)\(dv=e^{−st}dt\)\(v=−\frac{1}{s}e^{−st}\).

Ensuite, nous obtenons

\[ \begin{align*} \lim_{z→∞}\int ^z_0te^{−st}dt =\lim_{z→∞}[[−\frac{t}{s}e^{−st}]∣^z_0+\frac{1}{s}\int ^z_0e^{−st}dt] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}+\frac{0}{s}e^{−0s}]+\frac{1}{s}\int ^z_0e^{−st}dt] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}+0]−\frac{1}{s}[\frac{e^{−st}}{s}]∣^z_0] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}]−\frac{1}{s^2}[e^{−sz}−1]] \\[4pt]\ =\lim_{z→∞}[−\frac{z}{se^{sz}}]−\lim_{z→∞}[\frac{1}{s^2e^{sz}}]+\lim_{z→∞}\frac{1}{s^2} \\[4pt]\ =0−0+\frac{1}{s^2} \\[4pt]\ =\frac{1}{s^2}. \end{align*}\]

1. Calculez la transformée de Laplace de\(f(t)=1.\)
2. Calculez la transformée de Laplace de\(f(t)=e^{−3t}.\)
3. Calculez la transformée de Laplace de\(f(t)=t^2\). (Notez que vous devrez effectuer une intégration par parties deux fois.)

Les transformées de Laplace sont souvent utilisées pour résoudre des équations différentielles. Les équations différentielles ne seront abordées en détail que plus tard dans ce livre ; mais, pour l'instant, examinons la relation entre la transformée de Laplace d'une fonction et la transformée de Laplace de sa dérivée.

Commençons par la définition de la transformée de Laplace. Nous avons

\[L{f(t)}=\int ^∞_0e^{−st}f(t)dt=\lim_{z→∞}\int ^z_0e^{−st}f(t)dt. \nonumber \]

Utilisez l'intégration par parties pour évaluer\(\displaystyle \lim_{z→∞}\int ^z_0e^{−st}f(t)dt\). (Laissez\(u=f(t)\) et\(dv=e^{−st}dt\).)

Après l'intégration par parties et l'évaluation de la limite, vous devriez voir que

\[L{f(t)}=\frac{f(0)}{s}+\frac{1}{s}[L{f′(t)}]. \nonumber \]

Ensuite,

\[L{f′(t)}=sL{f(t)}−f(0). \nonumber \]

Ainsi, la différenciation dans le domaine temporel se simplifie en multiplication par s dans le domaine fréquentiel.

La dernière chose que nous examinons dans ce projet est de savoir comment les transformations de Laplace\(f(t)\) et ses propriétés antidérivées sont liées. Laissez\(g(t)=\int ^t_0f(u)du.\) alors,

\[L{g(t)}=\int ^∞_0e^{−st}g(t)dt=\lim_{z→∞}\int ^z_0e^{−st}g(t)dt. \nonumber \]

Utilisez l'intégration par parties pour évaluer\(\displaystyle \lim_{z→∞}\int ^z_0e^{−st}g(t)dt.\) (\(u=g(t)\)Let et\(dv=e^{−st}dt\). (Notez, d'ailleurs, que nous avons défini\(g(t), du=f(t)dt.\))

Comme vous pouvez vous y attendre, vous devriez voir que

\[L{g(t)}=\frac{1}{s}⋅L{f(t)}. \nonumber \]

L'intégration dans le domaine temporel permet de simplifier la division par\(s\) dans le domaine des fréquences.

Concepts clés

• Les intégrales de fonctions sur des intervalles infinis sont définies en termes de limites.
• Les intégrales de fonctions sur un intervalle pour lequel la fonction présente une discontinuité à une extrémité peuvent être définies en termes de limites.
• La convergence ou la divergence d'une intégrale incorrecte peut être déterminée en la comparant à la valeur d'une intégrale impropre pour laquelle la convergence ou la divergence est connue.

Équations clés

• Intégrales incorrectes

\(\displaystyle \int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx\)

\(\displaystyle \int ^b_{−∞}f(x)\,dx=\lim_{t→−∞}\int ^b_tf(x)\,dx\)

\(\displaystyle \int ^{+∞}_{−∞}f(x)\,dx=\int ^0_{−∞}f(x)\,dx+\int ^{+∞}_0f(x)\,dx\)

Lexique

intégrale inappropriée

une intégrale sur un intervalle infini ou une intégrale d'une fonction contenant une discontinuité infinie sur l'intervalle ; une intégrale impropre est définie en termes de limite. L'intégrale impropre converge si cette limite est un nombre réel fini ; sinon, l'intégrale impropre diverge