7.6 : Intégration numérique
- Page ID
- 197597
- Approximation de la valeur d'une intégrale définie en utilisant les règles du point médian et du trapèze.
- Déterminez l'erreur absolue et relative lors de l'utilisation d'une technique d'intégration numérique.
- Estimez l'erreur absolue et relative à l'aide d'une formule liée aux erreurs.
- Reconnaissez lorsque les règles du point médian et du trapèze surestiment ou sous-estiment la valeur réelle d'une intégrale.
- Utilisez la règle de Simpson pour approximer la valeur d'une intégrale définie avec une précision donnée.
Les antidérivés de nombreuses fonctions ne peuvent pas être exprimés ou ne peuvent pas être exprimés facilement sous forme fermée (c'est-à-dire en termes de fonctions connues). Par conséquent, plutôt que d'évaluer directement les intégrales définies de ces fonctions, nous avons recours à diverses techniques d'intégration numérique pour approximer leurs valeurs. Dans cette section, nous explorons plusieurs de ces techniques. De plus, nous examinons le processus d'estimation de l'erreur à l'aide de ces techniques.
La règle du point médian
Plus tôt dans ce texte, nous avons défini l'intégrale définie d'une fonction sur un intervalle comme la limite des sommes de Riemann. En général, toute somme Riemann d'une fonction\( f(x)\) sur un intervalle\([a,b]\) peut être considérée comme une estimation de\(\displaystyle ∫^b_af(x)\,dx\). Rappelons qu'une somme Riemann d'une fonction\( f(x)\) sur un intervalle\( [a,b]\) est obtenue en sélectionnant une partition.
\[ P=\{x_0,x_1,x_2,…,x_n\} \nonumber \]
où\(\quad a=x_0<x_1<x_2<⋯<x_n=b \)
et un set
\[ S=\{x^*_1,x^*_2,…,x^*_n\} \nonumber \]
où\(x_{i−1}≤x^*_i≤x_i \quad \text{for all} \, i.\)
La somme de Riemann correspondant à la partition\(P\) et à l'ensemble\(S\) est donnée par\(\displaystyle \sum^n_{i=1}f(x^*_i)Δx_i\), où est\( Δx_i=x_i−x_{i−1},\) la longueur du\( i^{\text{th}}\) sous-intervalle.
La règle du point médian pour estimer une intégrale définie utilise une somme de Riemann avec des sous-intervalles de largeur égale et les points\( m_i\) médians de chaque sous-intervalle à la place de\( x^*_i\). Formellement, nous énonçons un théorème concernant la convergence de la règle du point médian comme suit.
Supposons que\( f(x)\) c'est continu\([a,b]\). \( n\)Soit un entier positif et\( Δx=\dfrac{b−a}{n}\). Si\( [a,b]\) est divisé en\( n\) sous-intervalles, chacun ayant une longueur\( Δx\), et\( m_i\) étant le point médian du\( i^{\text{th}}\) sous-intervalle, définissez
\[M_n=\sum_{i=1}^nf(m_i)Δx. \nonumber \]
Alors\(\displaystyle \lim_{n→∞}M_n=∫^b_af(x)\,dx.\)
Comme nous pouvons le voir\( f(x)≥0\) sur la figure\(\PageIndex{1}\), si\( [a,b]\) cette valeur est supérieure,\(\displaystyle \sum^n_{i=1}f(m_i)Δx\) correspond à la somme des aires des rectangles se rapprochant de la zone située entre le graphique de\( f(x)\) et l'\(x\)axe supérieur\([a,b]\). Le graphique montre les rectangles correspondant à\(M_4\) pour une fonction non négative sur un intervalle fermé.\([a,b].\)
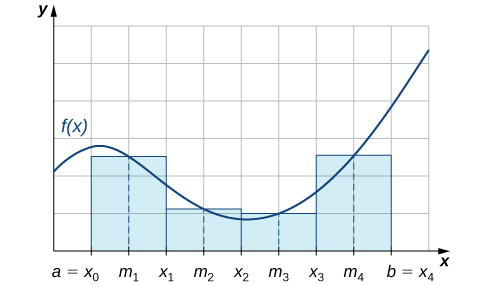
Utilisez la règle du point médian pour effectuer une estimation à\(\displaystyle ∫^1_0x^2\,dx\) l'aide de quatre sous-intervalles. Comparez le résultat avec la valeur réelle de cette intégrale.
Solution : Chaque sous-intervalle a une longueur.\( Δx=\dfrac{1−0}{4}=\dfrac{1}{4}.\) Par conséquent, les sous-intervalles se composent de
\[\left[0,\tfrac{1}{4}\right],\,\left[\tfrac{1}{4},\tfrac{1}{2}\right],\,\left[\tfrac{1}{2},\tfrac{3}{4}\right],\, \text{and}\, \left[\tfrac{3}{4},1\right].\nonumber \]
Les points médians de ces sous-intervalles sont\(\left\{\frac{1}{8},\,\frac{3}{8},\,\frac{5}{8},\, \frac{7}{8}\right\}.\) donc,
\[\begin{align*} M_4 &=\frac{1}{4}\cdot f\left(\frac{1}{8}\right)+\frac{1}{4}\cdot f\left(\frac{3}{8}\right)+\frac{1}{4}\cdot f\left(\frac{5}{8}\right)+\frac{1}{4}\cdot f\left(\frac{7}{8}\right) \\[4pt] &=\frac{1}{4}⋅\frac{1}{64}+\frac{1}{4}⋅\frac{9}{64}+\frac{1}{4}⋅\frac{25}{64}+\frac{1}{4}⋅\frac{49}{64}\\[4pt] &=\frac{21}{64} = 0.328125. \end{align*}\]
Depuis
\[ ∫^1_0x^2\,dx=\frac{1}{3},\nonumber \]
l'erreur absolue dans cette approximation est :
\[\left\lvert\dfrac{1}{3}−\dfrac{21}{64}\right\rvert=\dfrac{1}{192}≈0.0052, \nonumber \]
et nous voyons que la règle du point médian produit une estimation quelque peu proche de la valeur réelle de l'intégrale définie.
\(M_6\)À utiliser pour estimer la longueur de la courbe\(y=\frac{1}{2}x^2\) sur\([1,4]\).
Solution : La longueur d'\(y=\frac{1}{2}x^2\)un\([1,4]\) est
\[s = ∫^4_1\sqrt{1+\left(\frac{dy}{dx}\right)^2}\,dx.\nonumber \]
Depuis\(\dfrac{dy}{dx}=x\), cette intégrale devient\(\displaystyle ∫^4_1\sqrt{1+x^2}\,dx.\)
S'il\([1,4]\) est divisé en six sous-intervalles, chaque sous-intervalle a une longueur\(Δx=\dfrac{4−1}{6}=\dfrac{1}{2}\) et les points médians des sous-intervalles sont\(\left\{\frac{5}{4},\frac{7}{4},\frac{9}{4},\frac{11}{4},\frac{13}{4},\frac{15}{4}\right\}\). Si nous définissons\(f(x)=\sqrt{1+x^2}\),
\[\begin{align*} M_6 &=\tfrac{1}{2}\cdot f\left(\frac{5}{4}\right)+\tfrac{1}{2}\cdot f\left(\frac{7}{4}\right)+\frac{1}{2}\cdot f\left(\frac{9}{4}\right)+\frac{1}{2}\cdot f\left(\frac{11}{4}\right)+\frac{1}{2}\cdot f\left(\frac{13}{4}\right)+\frac{1}{2}\cdot f\left(\frac{15}{4}\right) \\[4pt] &≈\frac{1}{2}(1.6008+2.0156+2.4622+2.9262+3.4004+3.8810)=8.1431 \, \text{ units}. \end{align*}\]
Utilisez la règle du point médian avec\( n=2\) pour estimer\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Allusion
-
\( Δx=\frac{1}{2}, \quad m_1=\frac{5}{4},\quad \text{and} \quad m_2=\frac{7}{4}.\)
- Réponse
-
\(\dfrac{24}{35}\approx 0.685714\)
La règle trapézoïdale
Nous pouvons également approximer la valeur d'une intégrale définie en utilisant des trapèzes plutôt que des rectangles. Dans la figure\(\PageIndex{2}\), la zone située sous la courbe est approximée par des trapèzes plutôt que par des rectangles.
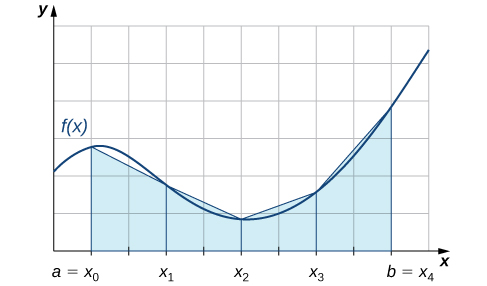
La règle trapézoïdale pour l'estimation des intégrales définies utilise des trapèzes plutôt que des rectangles pour approximer l'aire sous une courbe. Pour mieux comprendre la forme finale de la règle, considérez les trapèzes illustrés sur la figure\(\PageIndex{2}\). Nous supposons que la longueur de chaque sous-intervalle est donnée par\(Δx\). Tout d'abord, rappelons que l'aire d'un trapèze d'une hauteur\(h\) et d'une base de longueur\(b_1\) et\(b_2\) est donnée par\(\text{Area}=\frac{1}{2}h(b_1+b_2)\). On voit que le premier trapèze a une hauteur\(Δx\) et des bases parallèles de longueur\( f(x_0)\) et\( f(x_1)\). Ainsi, l'aire du premier trapèze de la figure\(\PageIndex{2}\) est
\[ \frac{1}{2}Δx\Big(f(x_0)+f(x_1)\Big).\nonumber \]
Les surfaces des trois trapèzes restants sont
\(\dfrac{1}{2}Δx\Big(f(x_1)+f(x_2)\Big),\, \dfrac{1}{2}Δx\Big(f(x_2)+f(x_3)\Big),\)et\( \dfrac{1}{2}Δx\Big(f(x_3)+f(x_4)\Big).\)
Par conséquent,
\[∫^b_af(x)\,dx≈\frac{1}{2}Δx\Big(f(x_0)+f(x_1)\Big)+\frac{1}{2}Δx\Big(f(x_1)+f(x_2)\Big)+\frac{1}{2}Δx\Big(f(x_2)+f(x_3)\Big)+\frac{1}{2}Δx\Big(f(x_3)+f(x_4)\Big).\nonumber \]
Après avoir éliminé un facteur commun\(\frac{1}{2}Δx\) et combiné des termes similaires, nous avons
\[ ∫^b_af(x)\,dx≈\frac{Δx}{2}\Big[f(x_0)+2\,f(x_1)+2\,f(x_2)+2\,f(x_3)+f(x_4)\Big].\nonumber \]
En général, nous énonçons formellement la règle suivante.
Supposons que\(f(x)\) c'est continu\([a,b]\). \(n\)Soit un entier positif et\(Δx=\dfrac{b−a}{n}\). \( [a,b]\)Soit divisé en\(n\) sous-intervalles, chacun de longueur\(Δx\), avec des extrémités à\( P=\{x_0,x_1,x_2…,x_n\}.\)
Set
\[T_n=\frac{Δx}{2}\Big[f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_{n−1})+f(x_n)\Big]. \nonumber \]
Ensuite,\(\displaystyle \lim_{n→+∞}T_n=∫^b_af(x)\,dx.\)
Avant de continuer, faisons quelques observations sur la règle trapézoïdale. Tout d'abord, il est utile de noter que
\(T_n=\dfrac{1}{2}(L_n+R_n)\)où\(\displaystyle L_n=\sum_{i=1}^nf(x_{i−1})Δx\) et\(\displaystyle R_n=\sum_{i=1}^nf(x_i)Δx.\)
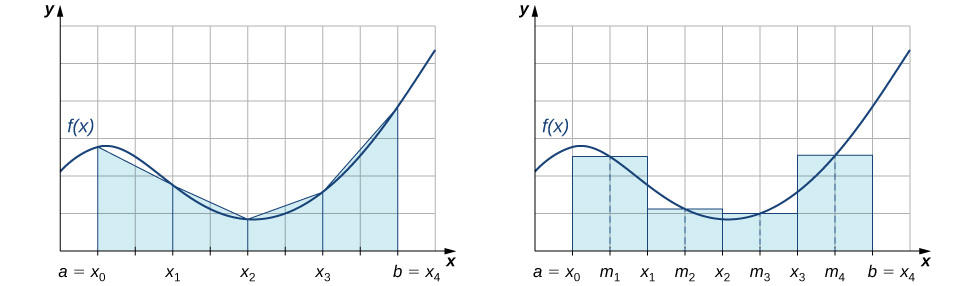
C'est-à-dire,\(L_n\) et\(R_n\) approximez l'intégrale en utilisant les extrémités gauche et droite de chaque sous-intervalle, respectivement. En outre, un examen attentif de la Figure nous\(\PageIndex{3}\) amène à faire les observations suivantes sur l'utilisation des règles trapézoïdales et des règles du point médian pour estimer l'intégrale définie d'une fonction non négative. La règle trapézoïdale tend à surestimer systématiquement la valeur d'une intégrale définie sur les intervalles où la fonction est concave vers le haut et à sous-estimer systématiquement la valeur d'une intégrale définie sur les intervalles où la fonction est concave vers le bas. D'autre part, la règle du point médian tend à modérer quelque peu ces erreurs en surestimant et en sous-estimant partiellement la valeur de l'intégrale définie sur ces mêmes types d'intervalles. Cela nous amène à émettre l'hypothèse qu'en général, la règle du point médian tend à être plus précise que la règle trapézoïdale.
Utilisez la règle trapézoïdale pour effectuer une estimation à\(\displaystyle ∫^1_0x^2\,dx\) l'aide de quatre sous-intervalles.
Solution
Les extrémités des sous-intervalles sont constituées d'éléments de l'ensemble\(P=\left\{0,\frac{1}{4},\, \frac{1}{2},\, \frac{3}{4},1\right\}\) et\(Δx=\frac{1−0}{4}=\frac{1}{4}.\) donc,
\ [\ begin {align*] ^1_0x^2dx &≈ \ frac {1} {2} ⋅ \ frac {1} {4} \ Big [f (0) +2 \, f \ left (\ tfrac {1} {4} \ right) +2 \, f \ left (\ tfrac {1} {2} \ right) +2 \, f \ left (\ tfrac {1} {2} \ right) +2 \, f \ left (\ tfrac {1} {2} \ right) +2 \, f \ left (\ tfrac {1} {2} ac {3} {4} \ droite) +f (1) \ [Grand] \ \ [4 points]
&= \ tfrac {1} {8} \ grand (0+2⋅ \ tfrac {1} {16} +2⋅ \ tfrac {1} {4} +2⋅ \ tfrac {9} {16} +1 \ gros) \\[4pt] &=\frac{11}{32} = 0.34375\end{align*}\]
Utilisez la règle trapézoïdale avec\( n=2\) pour estimer\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Allusion
-
Set\(Δx=\dfrac{1}{2}.\) Les extrémités des sous-intervalles sont les éléments de l'ensemble\(P=\left\{1,\frac{3}{2},2\right\}.\)
- Réponse
-
\(\dfrac{17}{24} \approx 0.708333\)
Erreur absolue et relative
Un aspect important de l'utilisation de ces règles d'approximation numérique consiste à calculer l'erreur liée à leur utilisation pour estimer la valeur d'une intégrale définie. Nous devons d'abord définir l'erreur absolue et l'erreur relative.
Si\(B\) notre estimation d'une quantité a une valeur réelle de\(A\), alors l'erreur absolue est donnée par\(|A−B|\).
L'erreur relative est l'erreur exprimée en pourcentage de la valeur réelle et est donnée par\[\left\lvert\frac{A−B}{A}\right\rvert⋅100\%. \nonumber \]
Calculez l'erreur absolue et relative dans l'estimation à\(\displaystyle ∫^1_0x^2\,dx\) l'aide de la règle du point médian, trouvée dans Exemple\(\PageIndex{1}\).
Solution : La valeur calculée est\(\displaystyle ∫^1_0x^2\,dx=\frac{1}{3}\) et notre estimation à partir de l'exemple l'est\(M_4=\frac{21}{64}\). Ainsi, l'erreur absolue est donnée par\(\left\lvert\frac{1}{3}−\frac{21}{64}\right\rvert=\frac{1}{192}≈0.0052.\)
L'erreur relative est\[\frac{1/192}{1/3}=\frac{1}{64}≈0.015625≈1.6\%.\nonumber \]
Calculez l'erreur absolue et relative dans l'estimation de\(\displaystyle ∫^1_0x^2\,dx\) l'utilisation de la règle trapézoïdale, trouvée dans l'exemple\(\PageIndex{3}\).
Solution : La valeur calculée est\(\displaystyle ∫^1_0x^2\,dx=\frac{1}{3}\) et notre estimation à partir de l'exemple l'est\(T_4=\frac{11}{32}\). Ainsi, l'erreur absolue est donnée par\(\left\lvert\frac{1}{3}−\frac{11}{32}\right\rvert=\frac{1}{96}≈0.0104.\)
L'erreur relative est donnée par\[\frac{1/96}{1/3}=0.03125≈3.1\%.\nonumber \]
Lors d'un précédent point de contrôle, nous avions estimé\(\displaystyle ∫^2_1\frac{1}{x}\,dx\)\(\frac{24}{35}\) utiliser\(M_2\). La valeur réelle de cette intégrale est\(\ln 2\). Utiliser\(\frac{24}{35}≈0.6857\) et\(\ln 2≈0.6931,\) calculer l'erreur absolue et l'erreur relative.
- Allusion
-
Utilisez les exemples précédents comme guide.
- Réponse
-
erreur absolue\(\approx 0.0074,\) et erreur relative\(\approx 1.1\%\)
Bornes d'erreur sur les règles du point médian et du trapèze
Dans les deux exemples précédents, nous avons pu comparer notre estimation d'une intégrale avec la valeur réelle de l'intégrale ; toutefois, nous ne pouvons généralement pas nous permettre ce luxe. En général, si nous approximons une intégrale, nous le faisons parce que nous ne pouvons pas calculer facilement la valeur exacte de l'intégrale elle-même. Par conséquent, il est souvent utile de pouvoir déterminer la limite supérieure de l'erreur dans une approximation d'une intégrale. Le théorème suivant fournit des limites d'erreur pour les règles du point médian et du trapèze. Le théorème est énoncé sans preuve.
\(f(x)\)Soit une fonction continue sur\([a,b]\), ayant une dérivée seconde\(f''(x)\) sur cet intervalle. Si\(M\) est la valeur maximale de\(|f''(x)|\) over\([a,b]\), alors les limites supérieures de l'erreur d'utilisation\(M_n\) et\(T_n\) d'estimation\(\displaystyle ∫^b_af(x)\,dx\) sont
\[\text{Error in}\, M_n≤\frac{M(b−a)^3}{24n^2}\label{MidError} \]
et
\[\text{Error in}\, T_n≤\frac{M(b−a)^3}{12n^2} \nonumber \].
Nous pouvons utiliser ces limites pour déterminer la valeur\(n\) nécessaire pour garantir que l'erreur dans une estimation est inférieure à une valeur spécifiée.
Quelle valeur de\(n\) doit être utilisée pour garantir l'exactitude d'\(\displaystyle ∫^1_0e^{x^2}\,dx\)une estimation de\(0.01\) si nous utilisons la règle du point médian ?
Solution
Nous commençons par déterminer la valeur de\(M\), la valeur maximale de\( |f''(x)|\) over\( [0,1]\) for\( f(x)=e^{x^2}\). Puisque\( f′(x)=2xe^{x^2},\) nous avons
\[ f''(x)=2e^{x^2}+4x^2e^{x^2}.\nonumber \]
Ainsi,
\[ |f''(x)|=2e^{x^2}(1+2x^2)≤2⋅e⋅3=6e.\nonumber \]
À partir de l'équation liée aux erreurs\(\ref{MidError}\), nous avons
\[ \text{Error in}\, M_n≤\frac{M(b−a)^3}{24n^2}≤\frac{6e(1−0)^3}{24n^2}=\frac{6e}{24n^2}.\nonumber \]
Nous résolvons maintenant l'inégalité suivante pour\(n\) :
\[\frac{6e}{24n^2}≤0.01.\nonumber \]
Ainsi,\(n≥\sqrt{\frac{600e}{24}}≈8.24.\) puisque\(n\) doit être un entier satisfaisant cette inégalité, le choix de\(n=9\) garantirait que
\[ \left\lvert ∫^1_0e^{x^2}\,dx−M_n \right\rvert <0.01.\nonumber \]
Analyse
Nous aurions peut-être été tentés d'arrondir\(8.24\) vers le bas et de choisir\(n=8\), mais ce serait incorrect car nous devons avoir un entier supérieur ou égal à\(8.24\). Nous devons garder à l'esprit que les estimations d'erreur fournissent une limite supérieure uniquement pour l'erreur. L'estimation réelle peut en fait être une bien meilleure approximation que celle indiquée par la limite d'erreur.
Utilisez l'équation\(\ref{MidError}\) pour déterminer la limite supérieure de l'erreur lors de l'utilisation\(M_4\) pour estimer\(\displaystyle ∫^1_0x^2\,dx.\)
- Allusion
-
\(f''(x)=2,\)donc\(M=2.\)
- Réponse
-
\(\dfrac{1}{192}\)
Règle de Simpson
Avec la règle du point médian, nous avons estimé les surfaces des régions situées sous des courbes à l'aide de rectangles. Dans un sens, nous avons approximé la courbe à l'aide de fonctions constantes par morceaux. Avec la règle trapézoïdale, nous avons approximé la courbe en utilisant des fonctions linéaires par morceaux. Et si nous devions plutôt approximer une courbe en utilisant des fonctions quadratiques par morceaux ? Avec la règle de Simpson, c'est exactement ce que nous faisons. Nous divisons l'intervalle en un nombre pair de sous-intervalles, chacun de largeur égale. Sur la première paire de sous-intervalles\(\displaystyle ∫^{x_2}_{x_0}f(x)\,dx\) avec laquelle nous faisons une approximation\(\displaystyle ∫^{x_2}_{x_0}p(x)\,dx\), où\(p(x)=Ax^2+Bx+C\) est la fonction quadratique passant par\((x_0,f(x_0)), \,(x_1,f(x_1)),\) et\((x_2,f(x_2))\) (Figure\(\PageIndex{4}\)). Au cours de la paire suivante de sous-intervalles, nous nous\(\displaystyle ∫^{x_4}_{x_2}f(x)\,dx\) rapprochons de l'intégrale d'une autre fonction quadratique qui passe par\( (x_2,f(x_2)), \,(x_3,f(x_3)),\) et\((x_4,f(x_4)).\) ce processus se poursuit avec chaque paire successive de sous-intervalles.
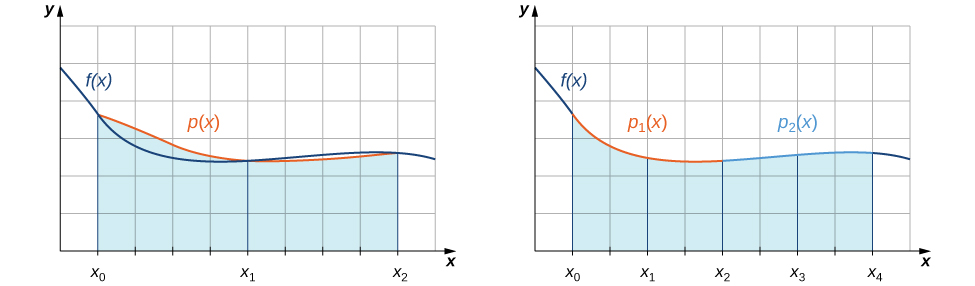
Pour comprendre la formule que nous obtenons pour la règle de Simpson, nous commençons par dériver une formule pour cette approximation sur les deux premiers sous-intervalles. Au cours de la dérivation, nous devons garder à l'esprit les relations suivantes :
\[f(x_0)=p(x_0)=Ax_0^2+Bx_0+C \nonumber \]
\[f(x_1)=p(x_1)=Ax_1^2+Bx_1+C \nonumber \]
\[f(x_2)=p(x_2)=Ax_2^2+Bx_2+C \nonumber \]
\(x_2−x_0=2Δx\), où\(Δx\) est la longueur d'un sous-intervalle.
\(x_2+x_0=2x_1,\)depuis\(x_1=\dfrac{(x_2+x_0)}{2}\).
Ainsi,
\ [\ begin {align*} ^^ {x_2} _ {x_0} f (x) \, dx &±^ {x_2} _ {x_0} p (x) \, dx \ \ [4 points]
&=^ {x_2} _ {x_0} (Ax^2+Bx+C) \, dx \ \ [4 points] &= {x_0} (Ax^2+Bx+C) \, dx \ \ [4 points]
&= \ left \ frac {A} {3} x^3+ \ frac {B} {2} x^2+CX \ right) \ bigg|^ {x_2} _ {x_0} & & \ text {Trouvez l'antidérivé.} \ \ [4pt]
&= \ frac {A} {3} (x_2^3−x_0^3) + \ frac {B} {2} (x_2^2−x_0^2) +C (x_2−x_0) & & \ text {Évaluez l'antidérivé.} \ \ [4pt]
&= \ frac {A} {3} (x_2−x_0) (x_2−x_2+x_2x_0+x_0^2) + \ {frac B} {2} (x_2−x_0) (x_2+x_0) +C (x_2−x_0) \ \ [4 points]
&= \ frac {x_2−x_0} {6} \ bigg (2A (x_2^2+x_2x_0+x_0^2) +3B (x_2+x_0) +6C \ bigg) & & \ text {Facteur out} \, \ frac {x_2−x_0} {6}. \ \ [4 points]
&= \ frac {Δx} {3} \ bigg ((Ax_2^2+Bx_2+C) + (Ax_0^2+Bx_0+C) +A (x_2^2+2x_2x_0+x_0^2) +2B (x_2+x_0) +4C \ bigg) & \ text {Réorganisez les termes. Remarque :} \ enspace Δx = \ frac {x_2−x_0} {2} \ \ [4pt]
&= \ frac {Δx} {3} \ big (f (x_2) +f (x_0) +A (x_2+x_0) ^2+2B (x_2+x_0) +4C \ big) & & \ text {Facteur et substitut :} \ \ [4 points]
& & & \ quad f (x_2) =Ax_2^2+Bx_2+C \ enspace \ text {et} \ enspace f (x_0) =Ax_0^2+Bx_0+C. \ \ [4 points]
&= \ frac {Δx} {3} \ big (f (x_2) +f (x_0) +A (2x_1) ^2+2B (2x_1) +4C \ big) & \ text {Substitut} \, x_2+x_0=2x_1. \ \ [4 points]
& & & \ quad \ text {Remarque :} \, x_1 = fr_1 \ ac {x_2+x_0} {2} \ enspace \ text {est le point médian.} \ \ [4pt]
&= \ frac {Δx} {3} \ big (f (x_2) +4f (x_1) +f (x_0) \ big). & & \ text {Développer et remplacer} \, f (x_1) =Ax_1^2+Bx_1+C. \ end {align*} \]
Si nous\(\displaystyle ∫^{x_4}_{x_2}f(x)\,dx\) utilisons la même méthode approximative, nous voyons que nous avons
\[∫^{x_4}_{x_2}f(x)\,dx≈\frac{Δx}{3}(f(x_4)+4\,f(x_3)+f(x_2)).\nonumber \]
En combinant ces deux approximations, nous obtenons
\[∫^{x_4}_{x_0}f(x)\,dx≈\frac{Δx}{3}(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+f(x_4)).\nonumber \]
Le schéma se poursuit lorsque nous ajoutons des paires de sous-intervalles à notre approximation. La règle générale peut être énoncée comme suit.
Supposons que\(f(x)\) c'est continu\([a,b]\). \(n\)Soit un entier pair positif et\(Δx=\dfrac{b−a}{n}\). \([a,b]\)Soyons divisés en\(n\) sous-intervalles, chacun de longueur\(Δx\), avec des extrémités à\(P=\{x_0,x_1,x_2,…,x_n\}.\) Set
\[S_n=\frac{Δx}{3}\Big[f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\Big]. \nonumber \]
Ensuite,
\[\lim_{n→+∞}S_n=∫^b_af(x)\,dx.\nonumber \]
Tout comme la règle trapézoïdale est la moyenne des règles de gauche et de droite pour estimer des intégrales définies, la règle de Simpson peut être obtenue à partir du point médian et des règles trapézoïdales en utilisant une moyenne pondérée. On peut le montrer\(S_{2n}=\left(\frac{2}{3}\right)M_n+\left(\frac{1}{3}\right)T_n\).
Il est également possible de limiter l'erreur en utilisant la règle de Simpson pour approximer une intégrale définie. La limite de l'erreur est donnée par la règle suivante :
\(f(x)\)Soit une fonction continue sur le\([a,b]\) fait d'avoir une quatrième dérivée\( f^{(4)}(x)\),, sur cet intervalle. Si\(M\) est la valeur maximale de\(∣f^{(4)}(x)∣\) over\([a,b]\), alors la limite supérieure de l'erreur lors de l'utilisation\(S_n\) pour estimer\(\displaystyle ∫^b_af(x)\,dx\) est donnée par
\[\text{Error in}\, S_n≤\frac{M(b−a)^5}{180n^4}. \nonumber \]
\(S_2\)À utiliser pour approximer\(\displaystyle ∫^1_0x^3\,dx\). Estimez la limite de l'erreur dans\(S_2\).
Solution
Comme\([0,1]\) il est divisé en deux intervalles, chaque sous-intervalle a une longueur\(Δx=\frac{1−0}{2}=\frac{1}{2}\). Les points de terminaison de ces sous-intervalles sont\(\left\{0,\frac{1}{2},1\right\}\). Si nous définissons\(f(x)=x^3,\) alors
\[S_2=\frac{1}{3}⋅\frac{1}{2}(f(0)+4\,f(\frac{1}{2})+f(1))=\frac{1}{6}(0+4⋅\frac{1}{8}+1)=\frac{1}{4}.\nonumber \]
Depuis\( f^{(4)}(x)=0\) et par conséquent,\(M=0,\) nous constatons que
Erreur dans\(S_2≤\frac{0(1)^5}{180⋅2^4}=0.\)
Cette borne indique que la valeur obtenue par la règle de Simpson est exacte. Une vérification rapide permettra de vérifier que, en fait,\(\displaystyle ∫^1_0x^3\,dx=\frac{1}{4}.\)
\(S_6\)À utiliser pour estimer la longueur de la courbe\(y=\frac{1}{2}x^2\) sur\([1,4].\)
Solution
La longueur de\(y=\frac{1}{2}x^2\) plus\([1,4]\) est\(\displaystyle ∫^4_1\sqrt{1+x^2}\,dx\). Si nous\([1,4]\) divisons en six sous-intervalles, chaque sous-intervalle a une longueur\(Δx=\frac{4−1}{6}=\frac{1}{2}\) et les points d'extrémité des sous-intervalles sont\( \left\{1,\frac{3}{2},2,\frac{5}{2},3,\frac{7}{2},4\right\}.\) Setting\( f(x)=\sqrt{1+x^2}\),
\[S_6=\frac{1}{3}⋅\frac{1}{2}(f(1)+4f(\frac{3}{2})+2f(2)+4f(\frac{5}{2})+2f(3)+4f(\frac{7}{2})+f(4)).\nonumber \]
Après la substitution, nous avons
\[S_6=\frac{1}{6}(1.4142+4⋅1.80278+2⋅2.23607+4⋅2.69258+2⋅3.16228+4⋅3.64005+4.12311)≈8.14594\,\text{units}. \nonumber \]
\(S_2\)À utiliser pour estimer\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Allusion
-
\[S_2=\frac{1}{3}Δx\left(f(x_0)+4f(x_1)+f(x_2)\right) \nonumber \]
- Réponse
-
\(\frac{25}{36} \approx 0.694444\)
Concepts clés
- Nous pouvons utiliser l'intégration numérique pour estimer les valeurs d'intégrales définies lorsqu'une forme fermée de l'intégrale est difficile à trouver ou lorsqu'une valeur approximative seule de l'intégrale définie est nécessaire.
- Les techniques les plus couramment utilisées pour l'intégration numérique sont la règle du point médian, la règle trapézoïdale et la règle de Simpson.
- La règle du point médian se rapproche de l'intégrale définie à l'aide de régions rectangulaires tandis que la règle trapézoïdale se rapproche de l'intégrale définie à l'aide d'approximations trapézoïdales.
- La règle de Simpson se rapproche de l'intégrale définie en approximant d'abord la fonction d'origine à l'aide de fonctions quadratiques par morceaux.
Équations clés
- Règle du point médian
\(\displaystyle M_n=\sum^n_{i=1}f(m_i)Δx\)
- Règle trapézoïdale
\(T_n=\frac{Δx}{2}\Big[f(x_0)+2\,f(x_1)+2\,f(x_2)+⋯+2\,f(x_{n−1})+f(x_n)\Big]\)
- La règle de Simpson
\(S_n=\frac{Δx}{3}\Big[f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+4\,f(x_5)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\Big]\)
- Limite d'erreur pour la règle du point médian
Erreur dans\(M_n≤\dfrac{M(b−a)^3}{24n^2}\), où\(M\) est la valeur maximale de\(|f''(x)|\) over\([a,b]\).
- Erreur limitée pour la règle trapézoïdale
Erreur dans\(T_n≤\dfrac{M(b−a)^3}{12n^2}\), où\(M\) est la valeur maximale de\(|f''(x)|\) over\([a,b]\).
- Erreur liée à la règle de Simpson
Erreur dans\(S_n≤\dfrac{M(b−a)^5}{180n^4}\), où\(M\) est la valeur maximale de\(∣f^{(4)}(x)∣\) over\([a,b]\).
Lexique
- erreur absolue
- s'il s'\(B\)agit d'une estimation d'une quantité dont la valeur réelle est de\(A\), alors l'erreur absolue est donnée par\( |A−B|\)
- règle du point médian
- une règle qui utilise une somme de Riemann de la forme\(\displaystyle M_n=\sum^n_{i=1}f(m_i)Δx\), où\( m_i\) est le point médian du\(i^{\text{th}}\) sous-intervalle pour obtenir une approximation\(\displaystyle ∫^b_af(x)\,dx\)
- intégration numérique
- les diverses méthodes numériques utilisées pour estimer la valeur d'une intégrale définie, y compris la règle du point médian, la règle trapézoïdale et la règle de Simpson
- erreur relative
- erreur en pourcentage de la valeur réelle, donnée par\[\text{relative error}=\left|\frac{A−B}{A}\right|⋅100\%\nonumber \]
- La règle de Simpson
- une règle qui se rapproche\(\displaystyle ∫^b_af(x)\,dx\) en utilisant l'aire sous une fonction quadratique par morceaux.
L'approximation\(S_n\) de\(\displaystyle ∫^b_af(x)\,dx\) est donnée par\[S_n=\frac{Δx}{3}\big(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\big).\nonumber \]
- règle trapézoïdale
- une règle qui se rapproche\(\displaystyle ∫^b_af(x)\,dx\) en utilisant l'aire des trapèzes.
L'approximation\(T_n\) de\(\displaystyle ∫^b_af(x)\,dx\) est donnée par\[T_n=\frac{Δx}{2}\big(f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_{n−1})+f(x_n)\big).\nonumber \]
Contributeurs et attributions
- Template:ContribOpenStaxCalc
- Edited by Paul Seeburger (Monroe Community College). Notes added to development of area under a parabola and typos fixed in original text.


