7.4E : Exercices pour la section 7.4

Utilisez la décomposition par fractions partielles (ou une technique plus simple) pour exprimer la fonction rationnelle sous forme de somme ou de différence entre deux expressions rationnelles plus simples ou plus.

1)\(\dfrac{1}{(x−3)(x−2)}\)

2)\(\dfrac{x^2+1}{x(x+1)(x+2)}\)

Réponse

\(\dfrac{x^2+1}{x(x+1)(x+2)} \quad = \quad −\dfrac{2}{x+1}+\dfrac{5}{2(x+2)}+\dfrac{1}{2x}\)

3)\(\dfrac{1}{x^3−x}\)

4)\(\dfrac{3x+1}{x^2}\)

Réponse

\(\dfrac{3x+1}{x^2} \quad = \quad \dfrac{1}{x^2}+\dfrac{3}{x}\)

5)\(\dfrac{3x^2}{x^2+1}\) (Conseil : utilisez d'abord la division longue.)

6)\(\dfrac{2x^4}{x^2−2x}\)

Réponse

\(\dfrac{2x^4}{x^2−2x} \quad = \quad 2x^2+4x+8+\dfrac{16}{x−2}\)

7)\(\dfrac{1}{(x−1)(x^2+1)}\)

8)\(\dfrac{1}{x^2(x−1)}\)

Réponse

\(\dfrac{1}{x^2(x−1)} \quad = \quad −\dfrac{1}{x^2}−\dfrac{1}{x}+\dfrac{1}{x−1}\)

9)\(\dfrac{x}{x^2−4}\)

10)\(\dfrac{1}{x(x−1)(x−2)(x−3)}\)

Réponse

\(\dfrac{1}{x(x−1)(x−2)(x−3)} \quad = \quad −\dfrac{1}{2(x−2)}+\dfrac{1}{2(x−1)}−\dfrac{1}{6x}+\dfrac{1}{6(x−3)}\)

11)\(\dfrac{1}{x^4−1}=\dfrac{1}{(x+1)(x−1)(x^2+1)}\)

(12)\(\dfrac{3x^2}{x^3−1}=\dfrac{3x^2}{(x−1)(x^2+x+1)}\)

Réponse

\(\dfrac{3x^2}{x^3−1} \quad = \quad \dfrac{1}{x−1}+\dfrac{2x+1}{x^2+x+1}\)

13)\(\dfrac{2x}{(x+2)^2}\)

(14)\(\dfrac{3x^4+x^3+20x^2+3x+31}{(x+1)(x^2+4)^2}\)

Réponse

\(\dfrac{3x^4+x^3+20x^2+3x+31}{(x+1)(x^2+4)^2} \quad = \quad \dfrac{2}{x+1}+\dfrac{x}{x^2+4}−\dfrac{1}{(x^2+4)^2}\)

Dans les exercices 15 à 25, utilisez la méthode des fractions partielles pour évaluer chacune des intégrales suivantes.

15)\(\displaystyle ∫\frac{dx}{(x−3)(x−2)}\)

16)\(\displaystyle ∫\frac{3x}{x^2+2x−8}\,dx\)

Réponse

\(\displaystyle ∫\frac{3x}{x^2+2x−8}\,dx \quad = \quad 2\ln|x+4|+\ln|x-2|+C = \ln\left| (x+4)^2(x-2) \right| + C\)

17)\(\displaystyle ∫\frac{dx}{x^3−x}\)

18)\(\displaystyle ∫\frac{x}{x^2−4}\,dx\)

Réponse

Notez que vous n'avez pas besoin de fractions partielles ici. Nous utilisons une simple\(u\) substitution.
\(\displaystyle ∫\frac{x}{x^2−4}\,dx \quad = \quad \tfrac{1}{2}\ln|4−x^2|+C\)

19)\(\displaystyle ∫\frac{dx}{x(x−1)(x−2)(x−3)}\)

(20)\(\displaystyle ∫\frac{2x^2+4x+22}{x^2+2x+10}\,dx\)

Réponse

Notez que puisque le degré du numérateur est égal au degré du dénominateur, nous devons commencer par une division longue.
Notez ensuite que nous devrons utiliser le fait de compléter le carré pour continuer, car nous ne pouvons pas prendre en compte le trinôme dans le dénominateur.
\(\displaystyle ∫\frac{2x^2+4x+22}{x^2+2x+10}\,dx \quad = \quad 2\left(x+\tfrac{1}{3}\arctan\left(\frac{1+x}{3}\right)\right)+C\)

(21)\(\displaystyle ∫\frac{dx}{x^2−5x+6}\)

22)\(\displaystyle ∫\frac{2−x}{x^2+x}\,dx\)

Réponse

\(\displaystyle ∫\frac{2−x}{x^2+x}\,dx \quad = \quad 2\ln|x|−3\ln|1+x|+C = \ln\left| \frac{x^2}{(1+x)^3} \right|+C\)

23)\(\displaystyle ∫\frac{2}{x^2−x−6}\,dx\)

(24)\(\displaystyle ∫\frac{dx}{x^3−2x^2−4x+8}\)

Réponse

\(\displaystyle ∫\frac{dx}{x^3−2x^2−4x+8} \quad = \quad \tfrac{1}{16}\left(−\frac{4}{−2+x}−\ln|−2+x|+\ln|2+x|\right)+C = \tfrac{1}{16}\left(−\frac{4}{−2+x}+\ln\left| \frac{x+2}{x-2} \right|\right)+C\)

25)\(\displaystyle ∫\frac{dx}{x^4−10x^2+9}\)

Dans les exercices 26 à 29, évaluez les intégrales avec des facteurs quadratiques irréductibles dans les dénominateurs.

26)\(\displaystyle ∫\frac{2}{(x−4)(x^2+2x+6)}\,dx\)

Réponse

\(\displaystyle ∫\frac{2}{(x−4)(x^2+2x+6)}\,dx \quad = \quad \tfrac{1}{30}(−2\sqrt{5}\arctan\left[\frac{1+x}{\sqrt{5}}\right]+2\ln|−4+x|−\ln|6+2x+x^2|)+C\)

(27)\(\displaystyle ∫\frac{x^2}{x^3−x^2+4x−4}\,dx\)

28)\(\displaystyle ∫\frac{x^3+6x^2+3x+6}{x^3+2x^2}\,dx\)

Réponse

Notez que nous devons d'abord utiliser la division longue, car le degré du numérateur est supérieur au degré du dénominateur.
\(\displaystyle ∫\frac{x^3+6x^2+3x+6}{x^3+2x^2}\,dx \quad = \quad −\frac{3}{x}+4\ln|x+2|+x+C\)

(29)\(\displaystyle ∫\frac{x}{(x−1)(x^2+2x+2)^2}\,dx\)

Dans les exercices 30 à 32, utilisez la méthode des fractions partielles pour évaluer les intégrales.

(30)\(\displaystyle ∫\frac{3x+4}{(x^2+4)(3−x)}\,dx\)

Réponse

\(\displaystyle ∫\frac{3x+4}{(x^2+4)(3−x)}\,dx \quad = \quad −\ln|3−x|+\tfrac{1}{2}\ln|x^2+4|+C\)

31)\(\displaystyle ∫\frac{2}{(x+2)^2(2−x)}\,dx\)

32)\(\displaystyle ∫\frac{3x+4}{x^3−2x−4}\,dx\) (Conseil : utilisez le théorème des racines rationnelles.)

Réponse

\(\displaystyle ∫\frac{3x+4}{x^3−2x−4}\,dx \quad = \quad \ln|x−2|−\tfrac{1}{2}\ln|x^2+2x+2|+C\)

Dans les exercices 33 à 46, utilisez la substitution pour convertir les intégrales en intégrales de fonctions rationnelles. Utilisez ensuite des fractions partielles pour évaluer les intégrales.

33)\(\displaystyle ∫^1_0\frac{e^x}{36−e^{2x}}\,dx\) (Donnez la réponse exacte et l'équivalent décimal. Arrondir à cinq décimales.)

34)\(\displaystyle ∫\frac{e^x\,dx}{e^{2x}−e^x}\,dx\)

Réponse

\(\displaystyle ∫\frac{e^x\,dx}{e^{2x}−e^x}\,dx \quad = \quad −x+\ln|1−e^x|+C\)

35)\(\displaystyle ∫\frac{\sin x\,dx}{1−\cos^2x}\)

36)\(\displaystyle ∫\frac{\sin x}{\cos^2 x+\cos x−6}\,dx\)

Réponse

\(\displaystyle ∫\frac{\sin x}{\cos^2 x+\cos x−6}\,dx \quad = \quad \tfrac{1}{5}\ln\left|\frac{\cos x+3}{\cos x−2}\right|+C\)

37)\(\displaystyle ∫\frac{1−\sqrt{x}}{1+\sqrt{x}}\,dx\)

38)\(\displaystyle ∫\frac{dt}{(e^t−e^{−t})^2}\)

Réponse

\(\displaystyle ∫\frac{dt}{(e^t−e^{−t})^2} \quad = \quad \frac{1}{2−2e^{2t}}+C\)

39)\(\displaystyle ∫\frac{1+e^x}{1−e^x}\,dx\)

40)\(\displaystyle ∫\frac{dx}{1+\sqrt{x+1}}\)

Réponse

\(\displaystyle ∫\frac{dx}{1+\sqrt{x+1}} \quad = \quad 2\sqrt{1+x}−2\ln|1+\sqrt{1+x}|+C\)

41)\(\displaystyle ∫\frac{dx}{\sqrt{x}+\sqrt[4]{x}}\)

42)\(\displaystyle ∫\frac{\cos x}{\sin x(1−\sin x)}\,dx\)

Réponse

\(\displaystyle ∫\frac{\cos x}{\sin x(1−\sin x)}\,dx \quad = \quad \ln\left|\frac{\sin x}{1−\sin x}\right|+C\)

43)\(\displaystyle ∫\frac{e^x}{(e^{2x}−4)^2}\,dx\)

44)\(\displaystyle ∫_1^2\frac{1}{x^2\sqrt{4−x^2}}\,dx\)

Réponse

\(\displaystyle ∫_1^2\frac{1}{x^2\sqrt{4−x^2}}\,dx \quad = \quad \frac{\sqrt{3}}{4}\)

45)\(\displaystyle ∫\frac{1}{2+e^{−x}}\,dx\)

46)\(\displaystyle ∫\frac{1}{1+e^x}\,dx\)

Réponse

\(\displaystyle ∫\frac{1}{1+e^x}\,dx \quad = \quad x−\ln(1+e^x)+C\)

Dans les exercices 47 à 48, utilisez la substitution donnée pour convertir l'intégrale en intégrale d'une fonction rationnelle, puis évaluez.

47)\(\displaystyle ∫\frac{1}{t−\sqrt[3]{t}}\,dt; \quad t=x^3\)

48)\(\displaystyle ∫\frac{1}{\sqrt{x}+\sqrt[3]{x}}\,dx; \quad x=u^6\)

Réponse

\(\displaystyle ∫\frac{1}{\sqrt{x}+\sqrt[3]{x}}\,dx \quad = \quad 6x^{1/6}−3x^{1/3}+2\sqrt{x}−6\ln(1+x^{1/6})+C\)

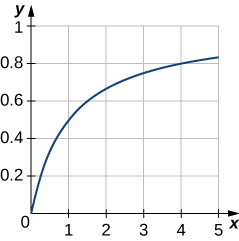
49) Tracez la courbe\(y=\dfrac{x}{1+x}\) sur l'intervalle\([0,5]\). Ensuite, trouvez l'aire de la région délimitée par la courbe, l'\(x\)axe et la ligne\(x=4\).

50) Déterminez le volume du solide généré lorsque la région délimitée par\(y=\dfrac{1}{\sqrt{x(3−x)}}, \,y=0, \,x=1,\) et\(x=2\) tourne autour de l'\(x\)axe.

Réponse

\(V = \frac{4}{3}π\text{arctanh}\,\left[\frac{1}{3}\right]=\frac{1}{3}π\ln 4 \, \text{units}^3\)

51) La vitesse d'une particule se déplaçant le long d'une ligne est fonction du temps donné par\(v(t)=\dfrac{88t^2}{t^2+1}.\) Trouver la distance parcourue par la particule après une\(t=5\) seconde.

Dans les exercices 52 à 54, résolvez le problème de la valeur initiale\(x\) en fonction de\(t\).

52)\((t^2−7t+12)\dfrac{dx}{dt}=1,\quad t>4,\, x(5)=0\)

Réponse

\( x=−\ln|t−3|+\ln|t−4|+\ln 2 = \ln\left| \dfrac{2(t-4)}{t-3}\right|\)

53)\((t+5)\dfrac{dx}{dt}=x^2+1, \quad t>−5,\,x(1)=\tan 1\)

(54)\((2t^3−2t^2+t−1)\dfrac{dx}{dt}=3,\quad x(2)=0\)

Réponse

\(x=\ln|t−1|−\sqrt{2}\arctan(\sqrt{2}t)−\frac{1}{2}\ln(t^2+\frac{1}{2})+\sqrt{2}\arctan(2\sqrt{2})+\frac{1}{2}\ln 4.5\)

55) Trouvez la\(x\) coordonnée du centroïde de la zone délimitée par\(y(x^2−9)=1, \, y=0, \,x=4,\) et\(x=5.\) (arrondissez la réponse à deux décimales.)

56) Trouvez le volume généré en faisant pivoter la zone délimitée par\(y=\dfrac{1}{x^3+7x^2+6x},\, x=1,\, x=7\) et\(y=0\) autour de l'\(y\)axe.

Réponse

\(V = \frac{2}{5}π\ln\frac{28}{13} \, \text{units}^3\)

57) Trouvez la zone délimitée par\(y=\dfrac{x−12}{x^2−8x−20}, \,y=0, \,x=2,\) et\(x=4\). (Arrondissez la réponse au centième le plus proche.)

58) Évaluer l'intégrale\(\displaystyle ∫\frac{dx}{x^3+1}.\)

Réponse

\(\displaystyle ∫\frac{dx}{x^3+1} \quad = \quad \frac{\arctan[\frac{−1+2x}{\sqrt{3}}]}{\sqrt{3}}+\frac{1}{3}\ln|1+x|−\frac{1}{6}\ln∣1−x+x^2∣+C\)

Pour les problèmes 59 à 62, utilisez les substitutions\(\tan(\frac{x}{2})=t, \,dx=\dfrac{2}{1+t^2}\,dt, \, \sin x=\dfrac{2t}{1+t^2},\) et\(\cos x=\dfrac{1−t^2}{1+t^2}.\)

59)\(\displaystyle ∫\frac{dx}{3−5\sin x}\)

60) Trouvez l'aire sous la courbe\(y=\dfrac{1}{1+\sin x}\) entre\(x=0\) et\(x=π.\) (Supposons que les dimensions soient en pouces.)

Réponse

2,0 pouces ²

61) Étant donné que les formules\(\tan\left(\frac{x}{2}\right)=t,\) sont dérivées\(dx=\dfrac{2}{1+t^2}dt, \,\sin x=\dfrac{2t}{1+t^2}\), et\(\cos x=\dfrac{1−t^2}{1+t^2}.\)

62) Évaluer\(\displaystyle ∫\frac{\sqrt[3]{x−8}}{x}\,dx.\)

Réponse

\(\displaystyle ∫\frac{\sqrt[3]{x−8}}{x}\,dx \quad = \quad 3(−8+x)^{1/3}−2\sqrt{3}\arctan\left[\frac{−1+(−8+x)^{1/3}}{\sqrt{3}}\right]−2\ln\left[2+(−8+x)^{1/3}\right]+\ln\left[4−2(−8+x)^{1/3}+(−8+x)^{2/3}\right]+C\)