7.3 : Substitution trigonométrique

Last updated
Save as PDF

Page ID: 197568

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

Résolvez les problèmes d'intégration impliquant la racine carrée d'une somme ou la différence de deux carrés.

Dans cette section, nous explorons les intégrales contenant des expressions de la forme\(\sqrt{a^2−x^2}\)\(\sqrt{a^2+x^2}\), et\(\sqrt{x^2−a^2}\), où les valeurs de\(a\) sont positives. Nous avons déjà rencontré et évalué des intégrales contenant certaines expressions de ce type, mais beaucoup restent encore inaccessibles. La technique de substitution trigonométrique est très pratique pour évaluer ces intégrales. Cette technique utilise la substitution pour réécrire ces intégrales en intégrales trigonométriques.

Intégrales impliquant\(\sqrt{a^2−x^2}\)

Avant de développer une stratégie générale pour les intégrales contenant\(\sqrt{a^2−x^2}\), considérez l'intégrale\(\displaystyle ∫\textstyle\sqrt{9−x^2}dx.\) Cette intégrale ne peut être évaluée à l'aide d'aucune des techniques dont nous avons discuté jusqu'à présent. Cependant, si nous faisons la substitution\(x=3\sin θ\), nous avons\(dx=3\cos θ \, dθ.\) Après la substitution dans l'intégrale, nous avons

\[ ∫\sqrt{9−x^2}\,dx=∫\textstyle\sqrt{ 9−(3\sin θ)^2}\cdot 3\cos θ \,dθ. \nonumber \]

Après avoir simplifié, nous avons

\[ ∫\sqrt{ 9−x^2}\,dx=∫ 9\textstyle\sqrt{1−\sin^2θ}\cdot\cos θ \, dθ. \nonumber \]

\(1−\sin^2θ=\cos^2θ,\)Laissons que nous avons maintenant

\[ ∫\sqrt{ 9−x^2}\,dx=∫ 9\textstyle\sqrt{\cos^2θ}\cos θ \, dθ. \nonumber \]

En supposant\(\cos θ≥0\) que nous avons

\[ ∫\textstyle\sqrt{ 9−x^2}\,dx=∫ 9\cos^2θ \, dθ. \nonumber \]

À ce stade, nous pouvons évaluer l'intégrale à l'aide des techniques développées pour intégrer les puissances et les produits des fonctions trigonométriques. Avant de terminer cet exemple, examinons la théorie générale qui sous-tend cette idée.

Pour évaluer les intégrales impliquant\(\sqrt{a^2−x^2}\), nous effectuons la substitution\(x=a\sin θ\) et\(dx=a\cos θ\). Pour voir que cela a vraiment du sens, considérez l'argument suivant : Le domaine de\(\sqrt{a^2−x^2}\) est\([−a,a]\). Ainsi,

\[−a≤x≤a. \nonumber \]

Par conséquent,

\[−1≤\dfrac{x}{a}≤1. \nonumber \]

Puisque la plage de\(\sin x\) dépassement\([−(π/2),π/2]\) est\([−1,1]\), il existe un angle unique\(θ\) satisfaisant de\(−(π/2)≤θ≤π/2\) telle sorte que\(\sin θ=x/a\), ou de manière équivalente, de sorte que\(x=a\sin θ\). Si nous le\(x=a\sin θ\) remplaçons par\(\sqrt{a^2−x^2}\), nous obtenons

\ [\ begin {align*} \ sqrt {a^2−x^2} &= \ sqrt {a^2− (a \ sin θ) ^2} & & \ text {Let} x=a \ sin θ \ text {où} − \ dfrac {π} {2} ≤θ≤ \ dfrac {π} {2}. \ \ [4pt]
& & & & \ {Texte Simplifier.} \ \ [4 points]
&= \ sqrt {a^2−a^2 \ sin^2θ} & & \ text {Facteur de sortie} a^2. \ \ [4 points]
&= \ sqrt {a^2 (1− \ sin^2θ)} & & \ text {Substitut} 1− \ sin^2x= \ cos^2x. \ \ [4pt]
&= \ sqrt {a^2 \ cos^2θ} & & \ text {Prenez la racine carrée.} \ \ [4 points]
&=|a \ cos θ| \ \ [4 points]
&=a \ cos θ \ end {align*} \]

Depuis\(\cos x≥0\) lors\(−\dfrac{π}{2}≤θ≤\dfrac{π}{2}\),\(a>0, |a\cos θ|=a\cos θ.\) nous pouvons voir, à partir de cette discussion, qu'en effectuant la substitution\(x=a\sin θ\), nous sommes capables de convertir une intégrale impliquant un radical en une intégrale impliquant des fonctions trigonométriques. Après avoir évalué l'intégrale, nous pouvons reconvertir la solution en une expression impliquant\(x\). Pour voir comment procéder, commençons par le supposer\(0<x<a\). Dans ce cas,\(0<θ<\dfrac{π}{2}\). Puisque\(\sin θ=\dfrac{x}{a}\), nous pouvons dessiner le triangle de référence dans la figure\(\PageIndex{1}\) pour aider à exprimer les valeurs\(\cos θ, \, \tan θ,\) et les fonctions trigonométriques restantes en termes de x. Il peut être démontré que ce triangle produit réellement les valeurs correctes des fonctions trigonométriques évaluées à\(θ\) pour tous ceux qui sont\(θ\) satisfaits\(−\dfrac{π}{2}≤θ≤\dfrac{π}{2}\). Il est utile de noter que l'expression apparaît\(\sqrt{a^2−x^2}\) réellement comme la longueur d'un côté du triangle. Enfin, devrait\(θ\) apparaître tout seul, nous utilisons\(θ=\sin^{−1}\left(\dfrac{x}{a}\right).\)

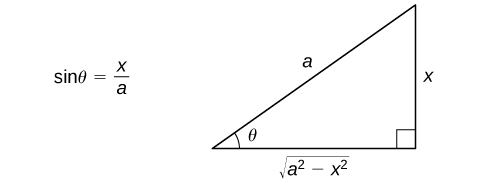
Cette figure est un triangle droit. Il a un angle étiqueté thêta. Cet angle est opposé au côté vertical. L'hypoténuse est étiquetée a, la jambe verticale est étiquetée x et la jambe horizontale est étiquetée comme la racine carrée de (a^2 — x^2). À gauche du triangle se trouve l'équation sin (theta) = x/a. — Figure\(\PageIndex{1}\) : Un triangle de référence peut aider à exprimer les fonctions trigonométriques évaluées\(θ\) en termes de\(x\).

L'essentiel de cette discussion est résumé dans la stratégie de résolution de problèmes suivante.

Stratégie de résolution de problèmes : intégrer des expressions impliquant\(\sqrt{a^2−x^2}\)

C'est une bonne idée de s'assurer que l'intégrale ne peut pas être évaluée facilement d'une autre manière. Par exemple, bien que cette méthode puisse être appliquée aux intégrales de la forme\(\displaystyle ∫\dfrac{1}{\sqrt{a^2−x^2}}dx\),\(\displaystyle ∫\dfrac{x}{\sqrt{a^2−x^2}}dx,\)\(\displaystyle ∫x\sqrt{a^2−x^2}\,dx,\) elles peuvent chacune être intégrées directement soit par une formule, soit par une simple\(u\) substitution.
Effectuez la substitution\(x=a \sin θ\) et\(dx=a\cos θ \,dθ.\) notez : Cette substitution donne\(\sqrt{a^2−x^2}=a\cos θ.\)
Simplifiez l'expression.
Évaluez l'intégrale à l'aide des techniques de la section sur les intégrales trigonométriques.
Utilisez le triangle de référence de la Figure 1 pour réécrire le résultat en termes de\(x\). Vous devrez peut-être également utiliser certaines identités trigonométriques et la relation\(θ=\sin^{−1}\left(\dfrac{x}{a}\right).\)

L'exemple suivant illustre l'application de cette stratégie de résolution de problèmes.

Exemple\(\PageIndex{1}\): Integrating an Expression Involving \(\sqrt{a^2−x^2}\)

Évaluer

\[ ∫\sqrt{ 9−x^2}dx. \nonumber \]

Solution

Commencez par effectuer les substitutions\(x=3\sin θ\) et\(\sin θ=\dfrac{x}{3}\),\(dx=3\cos θ \, dθ.\) depuis, nous pouvons construire le triangle de référence illustré à la Figure 2.

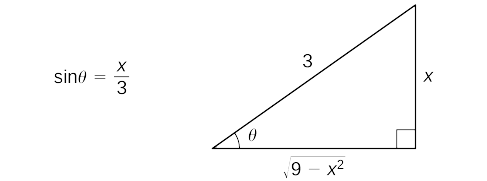
Cette figure est un triangle droit. Il a un angle étiqueté thêta. Cet angle est opposé au côté vertical. L'hypoténuse est étiquetée 3, la jambe verticale est étiquetée x et la jambe horizontale est étiquetée comme la racine carrée de (9 — x^2). À gauche du triangle se trouve l'équation sin (theta) = x/3. — Figure\(\PageIndex{2}\) : Un triangle de référence peut être construit par exemple\(\PageIndex{1}\).

Ainsi,

\[ ∫\sqrt{9−x^2}\,dx=∫\sqrt{ 9−(3\sin θ)^2}3\cos θ\,dθ \nonumber \]

Remplacer\(x=3\sin θ\) et\(dx=3\cos θ \,dθ\).

\(=∫\sqrt{ 9(1−\sin^2θ)}\cdot 3\cos θ \, dθ\)Simplifiez.

\(=∫\sqrt{ 9\cos^2θ}\cdot 3\cos θ \, dθ\)Substitut\(\cos^2θ=1−\sin^2θ\).

\(=∫ 3|\cos θ|3\cos θ \, dθ\)Prenez la racine carrée.

\(=∫ 9\cos^2θ \, dθ\)Simplifiez. Depuis\(−\dfrac{π}{2}≤θ≤\dfrac{π}{2},\cos θ≥0\) et\(|\cos θ|=\cos θ.\)

\(=∫ 9\left(\dfrac{1}{2}+\dfrac{1}{2}\cos(2θ)\right)\,dθ\)Utilisez la stratégie pour intégrer une puissance uniforme de\(\cos θ\).

\(=\dfrac{9}{2}θ+\dfrac{9}{4}\sin(2θ)+C\)Évaluez l'intégrale.

\(=\dfrac{9}{2}θ+\dfrac{9}{4}(2\sin θ\cos θ)+C\)

Substitut\(\sin(2θ)=2\sin θ\cos θ\).

\(=\dfrac{9}{2}\sin^{−1}\left(\dfrac{x}{3}\right)+\dfrac{9}{2}⋅\dfrac{x}{3}⋅\dfrac{\sqrt{9−x^2}}{3}+C\)Remplacer\(\sin^{−1}\left(\dfrac{x}{3}\right)=θ\) et\(\sin θ=\frac{x}{3}\). Utilisez le triangle de référence pour voir cela\(\cos θ=\dfrac{\sqrt{9−x^2}}{3} \) et effectuer cette substitution. Simplifiez.

\(=\dfrac{9}{2}\sin^{−1}\left(\dfrac{x}{3}\right)+\dfrac{x\sqrt{9−x^2}}{2}+C.\)Simplifiez.

Exemple\(\PageIndex{2}\): Integrating an Expression Involving \(\sqrt{a^2−x^2}\)

Évaluer

\[ ∫\dfrac{\sqrt{4−x^2}}{x}dx. \nonumber \]

Solution

Faites d'abord les substitutions\(x=2\sin θ\) et\(dx=2\cos θ\,dθ\). Depuis\(\sin θ=\dfrac{x}{2}\), nous pouvons construire le triangle de référence illustré sur la figure\(\PageIndex{3}\).

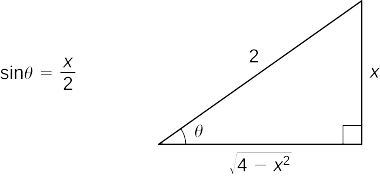
Cette figure est un triangle droit. Il a un angle étiqueté thêta. Cet angle est opposé au côté vertical. Le pied vertical est étiqueté x et le pied horizontal est étiqueté comme la racine carrée de (4 — x^2). À gauche du triangle se trouve l'équation sin (theta) = x/2. — Figure\(\PageIndex{3}\) : Un triangle de référence peut être construit par exemple\(\PageIndex{2}\).

Ainsi,

\(∫\dfrac{\sqrt{4−x^2}}{x}dx=∫\dfrac{\sqrt{4−(2\sin θ)^2}}{2\sin θ}2\cos θ \, dθ\)Substitut\(x=2\sin θ\) et\(dx=2\cos θ\,dθ.\)

\(=∫\dfrac{2\cos^2θ}{\sin θ}\,dθ\)Remplacez\(\cos^2θ=1−\sin^2θ\) et simplifiez.

\(=∫\dfrac{2(1−\sin^2θ)}{\sin θ}\,dθ\)Substitut\(\cos^2θ=1−\sin^2θ\).

\(=∫ (2\csc θ−2\sin θ)\,dθ\)Séparez le numérateur, simplifiez-le et utilisez-le\(\csc θ=\dfrac{1}{\sin θ}\).

\(=2 \ln |\csc θ−\cot θ|+2\cos θ+C\)Évaluez l'intégrale.

\(=2 \ln \left|\dfrac{2}{x}−\dfrac{\sqrt{4−x^2}}{x}\right|+\sqrt{4−x^2}+C.\)Utilisez le triangle de référence pour réécrire l'expression en termes\(x\) et pour la simplifier.

Dans l'exemple suivant, nous voyons que nous avons parfois le choix entre plusieurs méthodes.

Exemple\(\PageIndex{3}\): Integrating an Expression Involving \(\sqrt{a^2−x^2}\) Two Ways

Évaluez\(∫ x^3\sqrt{1−x^2}dx\) deux méthodes : d'abord en utilisant la substitution,\(u=1−x^2\) puis en utilisant une substitution trigonométrique.

Méthode 1

Laissez\(u=1−x^2\) et donc\(x^2=1−u\). Ainsi,\(du=−2x\,dx.\) dans ce cas, l'intégrale devient

\(∫ x^3\sqrt{1−x^2}\,dx=−\dfrac{1}{2}∫ x^2\sqrt{1−x^2}(−2x\,dx)\)Effectuez la substitution.

\(=−\dfrac{1}{2}∫ (1−u)\sqrt{u}\,du\)Développez l'expression.

\(=−\dfrac{1}{2}∫(u^{1/2}−u^{3/2})\,du\)Évaluez l'intégrale.

\(=−\dfrac{1}{2}(\dfrac{2}{3}u^{3/2}−\dfrac{2}{5}u^{5/2})+C\)Réécrivez en termes de x.

\(=−\dfrac{1}{3}(1−x^2)^{3/2}+\dfrac{1}{5}(1−x^2)^{5/2}+C.\)

Méthode 2

Laissez\(x=\sin θ\). Dans ce cas,\(dx=\cos θ \, dθ.\) en utilisant cette substitution, nous avons

\(∫ x^3\sqrt{1−x^2}dx=∫ \sin^3θ\cos^2θ \, dθ\)

\(=∫ (1−\cos^2θ)\cos^2θ\sin θ \, dθ\)\(u=\cos θ\)Laissons. Ainsi,\(du=−\sin θ \, dθ.\)

\(=∫ (u^4−u^2)\,du\)

\(=\dfrac{1}{5}u^5−\dfrac{1}{3}u^3+C\)substitut\(\cos θ=u.\)

\(=\dfrac{1}{5}\cos^5θ−\dfrac{1}{3}\cos^3θ+C\)Utilisez un triangle de référence pour voir que\(\cos θ=\sqrt{1−x^2}.\)

\(=\dfrac{1}{5}(1−x^2)^{5/2}−\dfrac{1}{3}(1−x^2)^{3/2}+C.\)

Exercice\(\PageIndex{1}\)

Réécrivez l'intégrale\(\displaystyle ∫\dfrac{x^3}{\sqrt{25−x^2}}\,dx\) en utilisant la substitution trigonométrique appropriée (n'évaluez pas l'intégrale).

Allusion: Substitut\(x=5\sin θ\) et\(dx=5\cos θ \, dθ.\)

Réponse: \(\displaystyle ∫ 125\sin^3θ \, dθ\)

Intégrer des expressions impliquant\(\sqrt{a^2+x^2}\)

Pour les intégrales contenant\(\sqrt{a^2+x^2}\), considérons d'abord le domaine de cette expression. Comme\(\sqrt{a^2+x^2}\) il est défini pour toutes les valeurs réelles de\(x\), nous limitons notre choix aux fonctions trigonométriques qui ont une plage de tous les nombres réels. Ainsi, notre choix se limite à sélectionner l'un\(x=a\tan θ\) ou l'autre\(x=a\cot θ\). L'une ou l'autre de ces substitutions fonctionnerait réellement, mais la substitution standard est\(x=a\tan θ\) ou, de manière équivalente,\(\tan θ=x/a\). Avec cette substitution, nous partons du principe que\(−(π/2)<θ<π/2\), de sorte que nous avons également\(θ=\tan^{−1}(x/a).\) La procédure d'utilisation de cette substitution est décrite dans la stratégie de résolution de problèmes suivante.

Stratégie de résolution de problèmes : intégrer des expressions impliquant\(\sqrt{a^2+x^2}\)

Vérifiez si l'intégrale peut être facilement évaluée en utilisant une autre méthode. Dans certains cas, il est plus pratique d'utiliser une méthode alternative.
Substituer\(x=a\tan θ\) et\(dx=a\sec^2θ \, dθ.\) Cette substitution donne\(\sqrt{a^2+x^2}=\sqrt{a^2+(a\tan θ)^2}=\sqrt{a^2(1+\tan^2θ)}=\sqrt{a^2sec^2θ}=|a\sec θ|=a\sec θ.\) (Depuis\(−\dfrac{π}{2}<θ<\dfrac{π}{2}\) et\(\sec θ>0\) pendant cet intervalle,\(|a\sec θ|=a\sec θ\).)
Simplifiez l'expression.
Évaluez l'intégrale à l'aide des techniques de la section sur les intégrales trigonométriques.
Utilisez le triangle de référence de la figure\(\PageIndex{4}\) pour réécrire le résultat en termes de\(x\). Vous devrez peut-être également utiliser certaines identités trigonométriques et la relation\(θ=\tan^{−1}\left(\dfrac{x}{a}\right)\). (Remarque : Le triangle de référence est basé sur l'hypothèse que\(x>0\), toutefois, les rapports trigonométriques produits à partir du triangle de référence sont les mêmes que les rapports pour lesquels\(x≤0\).)

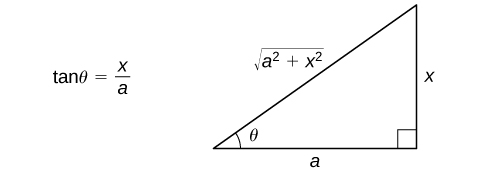
Cette figure est un triangle droit. Il a un angle étiqueté thêta. Cet angle est opposé au côté vertical. L'hypoténuse est appelée racine carrée de (a^2+x^2), la jambe verticale est désignée x et la jambe horizontale est étiquetée a. À gauche du triangle se trouve l'équation tan (theta) = x/a. À gauche du triangle se trouve l'équation tan (theta) = x/a. — Figure\(\PageIndex{4}\) : Un triangle de référence peut être construit pour exprimer les fonctions trigonométriques évaluées\(θ\) en termes de\(x\).

Exemple\(\PageIndex{4}\): Integrating an Expression Involving \(\sqrt{a^2+x^2}\)

Évaluez\(\displaystyle ∫\dfrac{dx}{\sqrt{1+x^2}}\) et vérifiez la solution en la différenciant.

Solution

Commencez par la substitution\(x=\tan θ\) et\(dx=sec^2θ\,dθ\). Depuis\(\tan θ=x\), dessinez le triangle de référence dans la figure\(\PageIndex{5}\).

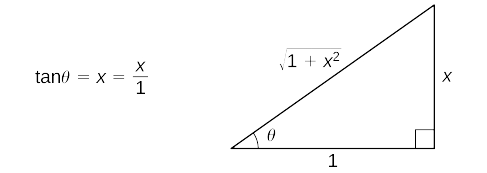
Cette figure est un triangle droit. Il a un angle étiqueté thêta. Cet angle est opposé au côté vertical. L'hypoténuse est étiquetée comme la racine carrée de (1+x^2), la jambe verticale est étiquetée x et la jambe horizontale est étiquetée 1. À gauche du triangle se trouve l'équation tan (theta) = x/1. — Figure\(\PageIndex{5}\) : Le triangle de référence par exemple\(\PageIndex{4}\).

Ainsi,

\ (\ displaystyle \ begin {align*} ∫ \ dfrac {dx} {\ sqrt {1+x^2}} &=∫ \ dfrac {\ sec^2θ} {\ sec θ} dθ & & & \ text {Substitut} x= \ tan θ \ text {et} dx= \ sec^2θ \, dθ. \ \ [4pt]
& & & & \ text {Cette substitution fait} \ sqrt {1+x^2} = \ sec θ. \ text {Simplifier.} \ \ [4pt]
&=∫ \ sec θ \, dθ & & \ text {Évaluez l'intégrale.} \ \ [4pt]
&= \ ln | \ sec θ+ \ tan θ|+C & & \ text {Utilisez le triangle de référence pour exprimer le résultat en termes de} x. \ \ [4 points]
&= \ ln | \ sqrt {1+x^2} +x|+c \ end {align*} \)

Pour vérifier la solution, différenciez :

\(\dfrac{d}{dx}\Big( \ln |\sqrt{1+x^2}+x|\Big)=\dfrac{1}{\sqrt{1+x^2}+x}⋅\left(\dfrac{x}{\sqrt{1+x^2}}+1\right) =\dfrac{1}{\sqrt{1+x^2}+x}⋅\dfrac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}}=\dfrac{1}{\sqrt{1+x^2}}.\)

Puisque\(\sqrt{1+x^2}+x>0\) pour toutes les valeurs de\(x\), nous pouvons réécrire\( \ln |\sqrt{1+x^2}+x|+C= \ln (\sqrt{1+x^2}+x)+C\), si vous le souhaitez.

Exemple\(\PageIndex{5}\): Evaluating \(∫\dfrac{dx}{\sqrt{1+x^2}}\) Using a Different Substitution

Utilisez la substitution\(x=\sinh θ\) pour évaluer\(\displaystyle ∫\dfrac{dx}{\sqrt{1+x^2}}.\)

Solution

Parce que\(\sinh θ\) possède une plage de tous les nombres réels, et\(1+\sinh^2θ=\cosh^2θ\), nous pouvons également utiliser la substitution\(x=\sinh θ\) pour évaluer cette intégrale. Dans ce cas,\(dx=\cosh θ \,dθ.\) par conséquent,

\ (\ displaystyle \ begin {align*} ∫ \ dfrac {dx} {\ sqrt {1+x^2}} &=∫ \ dfrac {\ cosh θ} {\ sqrt {1+ \ sinh^2θ}} dθ & & \ text {Substitut} x= \ sinh θ \ text {et} dx= \ cosh θ \, dθ. \ \ [4pt]
& & & \ text {Substitut} 1+ \ sinh^2θ= \ cosh^2θ. \ \ [4pt]
&=∫ \ dfrac {\ cosh θ} {\ sqrt {\ cosh^2θ}} dθ & amp ; & \ text {Depuis} \ sqrt {\ cosh^2θ} =| \ cosh θ| \ \ [4pt]
&=∫ \ dfrac {\ cosh θ} {| \ cosh θ|} dθ & & | \ cosh θ|= \ cosh θ \ text {depuis} \ cosh θ>0 \ text {pour tous} θ. \ \ [4pt]
&=∫ \ dfrac {\ cosh θ} {\ cosh θ} dθ & & \ text {Simplifier.} \ \ [4 points]
&=∫ 1 \, dθ & & \ text {Évaluez l'intégrale.} \ \ [4pt]
&=θ+C & & \ text {Depuis} x= \ sinh θ, \ text {nous savons} θ= \ sinh^ {−1} x. \ \ [4pt]
&= \ sinh^ {−1} x+C. \ end {align*} \)

Analyse

Cette réponse est très différente de la réponse obtenue à l'aide de la substitution.\(x=\tan θ.\) Pour voir que les solutions sont les mêmes, définissez\(y=\sinh^{−1}x\). Ainsi,\(\sinh y=x.\) à partir de cette équation, nous obtenons :

\[\dfrac{e^y−e^{−y}}{2}=x. \nonumber \]

Après avoir multiplié les deux côtés par\(2e^y\) et réécrit, cette équation devient :

\[e^{2y}−2xe^y−1=0. \nonumber \]

Utilisez l'équation quadratique pour résoudre les problèmes\(e^y\) suivants :

\[e^y=\dfrac{2x±\sqrt{4x^2+4}}{2}. \nonumber \]

Pour simplifier, nous avons :

\[e^y=x±\sqrt{x^2+1}. \nonumber \]

Depuis\(x−\sqrt{x^2+1}<0\), il doit être vrai que\(e^y=x+\sqrt{x^2+1}\). Ainsi,

\[y= \ln (x+\sqrt{x^2+1}). \nonumber \]

Enfin, nous obtenons

\[\sinh^{−1}x= \ln (x+\sqrt{x^2+1}). \nonumber \]

Après avoir fait la dernière observation selon laquelle, puisque\(x+\sqrt{x^2+1}>0,\)

\[ \ln (x+\sqrt{x^2+1})= \ln ∣\sqrt{1+x^2}+x∣, \nonumber \]

nous constatons que les deux méthodes différentes ont produit des solutions équivalentes.

Exemple\(\PageIndex{6}\): Finding an Arc Length

Détermine la longueur de la courbe\(y=x^2\) sur l'intervalle\([0,\dfrac{1}{2}]\).

Solution

Parce que\(\dfrac{dy}{dx}=2x\) la longueur de l'arc est donnée par

\[∫^{1/2}_0\sqrt{1+(2x)^2}dx=∫^{1/2}_0\sqrt{1+4x^2}dx. \nonumber \]

Pour évaluer cette intégrale, utilisez la substitution\(x=\dfrac{1}{2}\tan θ\) et\(dx=\tfrac{1}{2}\sec^2θ \, dθ\). Nous devons également modifier les limites de l'intégration. Si\(x=0\), alors\(θ=0\) et si\(x=\dfrac{1}{2}\), alors\(θ=\dfrac{π}{4}.\) Ainsi,

\(∫^{1/2}_0\sqrt{1+4x^2}dx=∫^{π/4}_0\sqrt{1+\tan^2θ}\cdot \tfrac{1}{2}\sec^2θ \, dθ\)Après substitution,\(\sqrt{1+4x^2}=\sec θ\). (Remplacez\(1+\tan^2θ=\sec^2θ\) et simplifiez.)

\(=\tfrac{1}{2}∫^{π/4}_0\sec^3θ \, dθ\)Nous avons dérivé cette intégrale dans la section précédente.

\(=\tfrac{1}{2}(\dfrac{1}{2}\sec θ\tan θ+ \dfrac{1}{2}\ln |\sec θ+\tan θ|)∣^{π/4}_0\)Évaluez et simplifiez.

\(=\tfrac{1}{4}(\sqrt{2}+ \ln (\sqrt{2}+1)).\)

Exercice\(\PageIndex{2}\)

Réécrivez\(\displaystyle ∫ x^3\sqrt{x^2+4}dx\) en utilisant une substitution impliquant\(\tan θ\).

Allusion: Utiliser\(x=2\tan θ\) et\(dx=2\sec^2θ \, dθ.\)

Réponse: \[ ∫ 32\tan^3θ\sec^3θ \, dθ \nonumber \]

Intégrer des expressions impliquant\(\sqrt{x^2−a^2}\)

Le domaine de l'expression\(\sqrt{x^2−a^2}\) est\((−∞,−a]∪[a,+∞)\). Ainsi, soit\(x\le −a\) soit\(x\ge a.\) d'où,\(\dfrac{x}{a}≤−1\) soit\(\dfrac{x}{a}≥1\). Puisque ces intervalles correspondent à la plage de\(\sec θ\) sur l'ensemble\([0,\dfrac{π}{2})∪(\dfrac{π}{2},π]\), il est logique d'utiliser la substitution\(\sec θ=\dfrac{x}{a}\) ou, de manière équivalente\(x=a\sec θ\), où\(0≤θ<\dfrac{π}{2}\) ou\(\dfrac{π}{2}<θ≤π\). La substitution correspondante pour\(dx\) est\(dx=a\sec θ\tan θ \, dθ\). La procédure d'utilisation de cette substitution est décrite dans la stratégie de résolution de problèmes suivante.

Stratégie de résolution de problèmes : intégrales impliquant\(\sqrt{x^2−a^2}\)

Vérifiez si l'intégrale ne peut pas être évaluée à l'aide d'une autre méthode. Dans l'affirmative, nous souhaiterons peut-être envisager d'appliquer une autre technique.
Remplacer\(x=a\sec θ\) et\(dx=a\sec θ\tan θ \, dθ\). Cette substitution donne\[ \sqrt{x^2−a^2}=\sqrt{(a\sec θ)^2−a^2}=\sqrt{a^2(\sec^2θ-1)}=\sqrt{a^2\tan^2θ}=|a\tan θ|. \nonumber \] Pour\(x≥a, |a\tan θ|=a\tan θ\) et pour\(x≤−a, |a\tan θ|=−a\tan θ.\)
Simplifiez l'expression.
Évaluez l'intégrale à l'aide des techniques de la section sur les intégrales trigonométriques.
Utilisez les triangles de référence de la figure\(\PageIndex{6}\) pour réécrire le résultat en termes de\(x\).
Vous devrez peut-être également utiliser certaines identités trigonométriques et la relation\(θ=\sec^{−1}\left(\dfrac{x}{a}\right)\). (Remarque : nous avons besoin des deux triangles de référence, car les valeurs de certains rapports trigonométriques sont différentes selon que oui\(x>a\) ou non\(x<−a\).)

Cette figure comporte deux triangles droits. Le premier triangle se trouve dans le premier quadrant du système de coordonnées xy et possède un angle intitulé thêta. Cet angle est opposé au côté vertical. L'hypoténuse est étiquetée x, la jambe verticale est étiquetée la racine carrée de (x^2-a^2) et la jambe horizontale est étiquetée a. La jambe horizontale se trouve sur l'axe des abscisses. À gauche du triangle se trouve l'équation sec (theta) = x/a, x — Figure\(\PageIndex{6}\) : Utilisez le triangle de référence approprié pour exprimer les fonctions trigonométriques évaluées\(θ\) en termes de\(x\).

Exemple\(\PageIndex{7}\): Finding the Area of a Region

Détermine l'aire de la région située entre le graphique de\(f(x)=\sqrt{x^2−9}\) et l'axe X sur l'intervalle\([3,5].\)

Solution

Tout d'abord, tracez un graphique approximatif de la région décrite dans le problème, comme le montre la figure suivante.

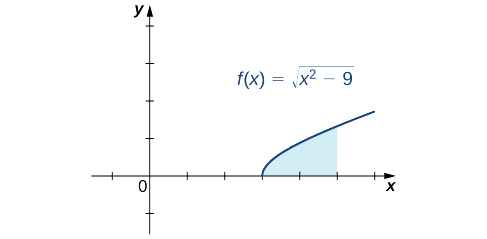
Cette figure est le graphique de la fonction f (x) = la racine carrée de (x^2-9). Il s'agit d'une courbe croissante qui commence sur l'axe X en 3 et se trouve dans le premier quadrant. Sous la courbe au-dessus de l'axe X se trouve une région ombrée délimitée vers la droite en x = 5. — Figure\(\PageIndex{7}\) : Le calcul de l'aire de la région ombrée nécessite l'évaluation d'une intégrale avec une substitution trigonométrique.

Nous pouvons voir que la région est\(A=∫^5_3\sqrt{x^2−9}dx\). Pour évaluer cette intégrale définie, remplacez\(x=3\sec θ\) et\(dx=3\sec θ\tan θ \, dθ\). Nous devons également modifier les limites de l'intégration. Si\(x=3\), alors\(3=3\sec θ\) et donc\(θ=0\). Si\(x=5\), alors\(θ=\sec^{−1}(\dfrac{5}{3})\). Après avoir effectué ces substitutions et simplifié, nous avons

Zone\(=∫^5_3\sqrt{x^2−9}dx\)

\(=∫^{\sec^{−1}(5/3)}_09\tan^2θ\sec θ \, dθ\)Utiliser\(\tan^2θ=\sec^2θ - 1.\)

\(=∫^{\sec^{−1}(5/3)}_09(\sec^2θ−1)\sec θ \, dθ\)Élargir.

\(=∫^{\sec^{−1}(5/3)}_09(\sec^3θ−\sec θ)\,dθ\)Évaluez l'intégrale.

\(=(\dfrac{9}{2} \ln |\sec θ+\tan θ|+\dfrac{9}{2}\sec θ\tan θ)−9 \ln |\sec θ+\tan θ|∣^{\sec^{−1}(5/3)}_0\)Simplifiez.

\(=\dfrac{9}{2}\sec θ\tan θ−\dfrac{9}{2} \ln |\sec θ+\tan θ|∣^{\sec^{−1}(5/3)}_0\)Évaluer. Utiliser\(\sec(\sec^{−1}\dfrac{5}{3})=\dfrac{5}{3}\) et\(\tan(\sec^{−1}\dfrac{5}{3})=\dfrac{4}{3}.\)

\(=\dfrac{9}{2}⋅\dfrac{5}{3}⋅\dfrac{4}{3}−\dfrac{9}{2} \ln ∣\dfrac{5}{3}+\dfrac{4}{3}∣−(\dfrac{9}{2}⋅1⋅0−\dfrac{9}{2} \ln |1+0|)\)

\(=10−\dfrac{9}{2} \ln 3\)

Exercice\(\PageIndex{3}\)

Évaluer\[∫\dfrac{dx}{\sqrt{x^2−4}}. \nonumber \] Supposons que\(x>2.\)

Allusion: Substitut\(x=2\sec θ\) et\(dx=2\sec θ\tan θ \, dθ.\)

Réponse: \[ \ln |\dfrac{x}{2}+\dfrac{\sqrt{x^2−4}}{2}|+C \nonumber \]

Concepts clés

Pour les intégrales impliquant\(\sqrt{a^2−x^2}\), utilisez la substitution\(x=a\sin θ\) et\(dx=a\cos θ \, dθ.\)
Pour les intégrales impliquant\(\sqrt{a^2+x^2}\), utilisez la substitution\(x=a\tan θ\) et\(dx=a\sec^2θ \, dθ\).
Pour les intégrales impliquant\(\sqrt{x^2−a^2}\), remplacez\(x=a\sec θ\) et\(dx=a\sec θ\tan θ \,dθ\).

Lexique

substitution trigonométrique: une technique d'intégration qui convertit une intégrale algébrique contenant des expressions de la forme\(\sqrt{a^2−x^2}\)\(\sqrt{a^2+x^2}\), ou\(\sqrt{x^2−a^2}\) en une intégrale trigonométrique