7.1 : Intégration par pièces
- Page ID
- 197625
- Déterminez quand utiliser l'intégration par pièces.
- Utilisez la formule d'intégration par parties pour résoudre les problèmes d'intégration.
- Utilisez la formule d'intégration par parties pour des intégrales définies.
Nous disposons maintenant d'une procédure assez complète pour évaluer de nombreuses intégrales de base. Cependant, bien que nous puissions intégrer en\(∫x \sin (x^2)\,dx\) utilisant la substitution\(u=x^2\), quelque chose d'aussi simple que cela nous\(∫x\sin x\,\,dx\) défie. De nombreux étudiants souhaitent savoir s'il existe une règle de produit pour l'intégration. Il n'y en a pas, mais il existe une technique basée sur la règle du produit pour la différenciation qui nous permet d'échanger une intégrale contre une autre. C'est ce que nous appelons l'intégration par pièces.
La formule d'intégration par pièces
Si\(h(x)=f(x)g(x)\), alors en utilisant la règle du produit, nous obtenons
\[h′(x)=f′(x)g(x)+g′(x)f(x). \label{eq1} \]
Bien que cela puisse sembler contre-productif au premier abord, intégrons maintenant les deux côtés de l'équation \ ref {eq1} :
\[∫h′(x)\,\,dx=∫(g(x)f′(x)+f(x)g′(x))\,\,dx. \nonumber \]
Cela nous donne
\[ h(x)=f(x)g(x)=∫g(x)f′(x)\,dx+∫f(x)g′(x)\,\,dx. \nonumber \]
Maintenant, nous résolvons\(∫f(x)g′(x)\,\,dx:\)
\[ ∫f(x)g′(x)\,dx=f(x)g(x)−∫g(x)f′(x)\,\,dx. \nonumber \]
En effectuant les substitutions\(u=f(x)\) et\(v=g(x)\), qui à leur tour, font\(du=f′(x)\,dx\) et\(dv=g′(x)\,dx\), nous obtenons la forme la plus compacte.
\[ ∫u\,dv=uv−∫v\,du. \nonumber \]
Fonctions\(u=f(x)\) Let and\(v=g(x)\) Be avec des dérivées continues. Ensuite, la formule d'intégration par parties pour l'intégrale impliquant ces deux fonctions est la suivante :
\[∫u\,dv=uv−∫v\,du. \label{IBP} \]
L'avantage de l'utilisation de la formule d'intégration par parties est que nous pouvons l'utiliser pour échanger une intégrale par une autre intégrale, peut-être plus simple. L'exemple suivant illustre son utilisation.
Utiliser l'intégration par pièces avec\(u=x\) et\(dv=\sin x\,\,dx\) pour évaluer
\[∫x\sin x\,\,dx. \nonumber \]
Solution
En choisissant\(u=x\), nous l'avons fait\(du=1\,\,dx\). Depuis\(dv=\sin x\,\,dx\), nous obtenons
\[v=∫\sin x\,\,dx=−\cos x. \nonumber \]
Il est pratique de suivre ces valeurs comme suit :
- \(u=x\)
- \(dv=\sin x\,\,dx\)
- \(du=1\,dx\)
- \(v=∫\sin x\,\,dx=−\cos x.\)
L'application de la formule d'intégration par parties (équation \ ref {IBP}) donne
\[ \begin{align} ∫x\sin x\,\,dx &=(x)(−\cos x)−∫(−\cos x)(1\,\,dx) \tag{Substitute} \\[4pt] &=−x\cos x+∫\cos x\,\,dx \tag{Simplify} \end{align} \]
Ensuite, utilisez
\[∫\cos x\,\,dx =\sin x+C. \nonumber \]
pour obtenir
\[∫x\sin x\,\,dx =−x\cos x+\sin x+C. \nonumber \]
Analyse
À ce stade, il y a probablement quelques points qui nécessitent des éclaircissements. Tout d'abord, vous êtes peut-être curieux de savoir ce qui se serait passé si nous avions choisi\(u=\sin x\) et\(dv=x\). Si nous l'avions fait, alors nous l'aurions fait\(du=\cos x\) et\(v=\dfrac{1}{2}x^2\). Ainsi, après avoir appliqué l'intégration par parties (équation \ ref {IBP}), nous avons
\[ ∫x\sin x\,\,dx=\dfrac{1}{2}x^2\sin x−∫\dfrac{1}{2}x^2\cos x\,\,dx. \nonumber \]
Malheureusement, avec la nouvelle intégrale, nous ne sommes pas dans une meilleure position qu'avant. Il est important de garder à l'esprit que lorsque nous appliquons l'intégration par parties, il se peut que nous devions essayer plusieurs choix\(dv\) avant de trouver un choix qui fonctionne.\(u\)
Ensuite, vous vous demandez peut-être pourquoi, lorsque nous trouvons\(v=∫\sin x\,\,dx=−\cos x\) que nous n'utilisons pas.\(v=−\cos x+K.\) Pour que cela ne fasse aucune différence, nous pouvons retravailler le problème en utilisant\(v=−\cos x+K\) :
\[ \begin{align*} ∫x\sin x\,\,dx &=(x)(−\cos x+K)−∫(−\cos x+K)(1\,\,dx) \\[4pt] &=−x\cos x+Kx+∫\cos x\,\,dx−∫K\,\,dx \\[4pt] &=−x\cos x+Kx+\sin x−Kx+C \\[4pt] &=−x\cos x+\sin x+C. \end{align*}\]
Comme vous pouvez le constater, cela ne fait aucune différence dans la solution finale.
Enfin, nous pouvons vérifier que notre antidérivé est correct en différenciant\(−x\cos x+\sin x+C:\)
\[ \begin{align*} \dfrac{d}{\,dx}(−x\cos x+\sin x+C) = \cancel{(−1)\cos x} + (−x)(−\sin x) + \cancel{\cos x} \\[4pt] =x\sin x \end{align*}\]
Par conséquent, l'antidérivé est vérifié.
Évaluez\(∫xe^{2x}\,dx\) à l'aide de la formule d'intégration par parties (équation \ ref {IBP}) avec\(u=x\) et\(dv=e^{2x}\,\,dx\).
- Allusion
-
Recherchez\(du\) et\(v\), et utilisez l'exemple précédent comme guide.
- Réponse
-
\[ ∫xe^{2x}\,\,dx=\dfrac{1}{2}xe^{2x}−\dfrac{1}{4}e^{2x}+C \nonumber \]
La question naturelle à se poser à ce stade est la suivante : comment savons-nous choisir\(u\) et\(dv\) ? Parfois, c'est une question d'essais et d'erreurs ; cependant, l'acronyme LIATE peut souvent aider à éliminer certaines conjectures de nos choix. Cet acronyme signifie les fonctions logarithmiques L, les fonctions trigonométriques inverses, les fonctions algébriques A, les fonctions rigonométriques T et les fonctions exponentielles E. Ce mnémotechnique aide à déterminer un choix approprié pour\(u\). Le type de fonction dans l'intégrale qui apparaît en premier dans la liste doit être notre premier choix\(u\).
Par exemple, si une intégrale contient une fonction logarithmique et une fonction algébrique, nous devons\(u\) choisir d'être la fonction logarithmique, car L vient avant A dans LIATE. L'intégrale de l'exemple\(\PageIndex{1}\) possède une fonction trigonométrique (\(\sin x\)) et une fonction algébrique (\(x\)). Comme A vient avant T dans LIATE, nous avons choisi\(u\) d'être la fonction algébrique. Lorsque nous avons choisi\(u\),\(dv\) est sélectionné pour être la partie restante de la fonction à intégrer, avec\(\,dx\).
Pourquoi ce mnémotechnique fonctionne-t-il ? N'oubliez pas que tout ce que nous choisissons d'être\(dv\) doit être quelque chose que nous pouvons intégrer. Comme nous ne disposons pas de formules d'intégration nous permettant d'intégrer des fonctions logarithmiques simples et des fonctions trigonométriques inverses, il est logique qu'elles ne soient pas choisies comme valeurs pour\(dv\). Par conséquent, ils devraient figurer en tête de liste en tant que choix pour\(u\). Ainsi, nous avons placé LI au début du mnémotechnique. (Nous aurions tout aussi bien pu commencer avec IL, car ces deux types de fonctions n'apparaîtront pas ensemble dans un problème d'intégration par pièces.) Les fonctions exponentielles et trigonométriques se situent à la fin de notre liste car elles sont assez faciles à intégrer et permettent de faire de bons choix\(dv\). Ainsi, nous avons TE à la fin de notre mnémotechnique. (Nous aurions tout aussi bien pu utiliser ET à la fin, car lorsque ces types de fonctions apparaissent ensemble, peu importe laquelle est\(u\) et laquelle l'est\(dv\).) Les fonctions algébriques sont généralement faciles à intégrer et à différencier, et elles se situent au milieu du mnémotechnique.
Évaluer\[∫\dfrac{\ln x}{x^3}\,\,dx. \nonumber \]
Solution
Commencez par réécrire l'intégrale :
\[∫\dfrac{\ln x}{x^3}\,\,dx=∫x^{−3}\ln x\,\,dx. \nonumber \]
Puisque cette intégrale contient la fonction algébrique\(x^{−3}\) et la fonction logarithmique\(\ln x\), choisissez\(u=\ln x\), car elle\(L\) précède A dans LIATE. Une fois que nous avons choisi\(u=\ln x\), nous devons choisir\(dv=x^{−3}\,dx\).
Ensuite, puisque\(u=\ln x,\) nous avons\(du=\dfrac{1}{x}\,dx.\) également,\(v=∫x^{−3}\,dx=−\dfrac{1}{2}x^{−2}.\) Résumant,
- \(u=\ln x\)
- \(du=\dfrac{1}{x}\,dx\)
- \(dv=x^{−3}\,dx\)
- \(v=∫x^{−3}\,dx=−\dfrac{1}{2}x^{−2}.\)
La substitution dans la formule d'intégration par parties (équation \ ref {IBP}) donne
\[ \begin{align*} ∫\dfrac{\ln x}{x^3}\,dx &=∫x^{−3}\ln x\,dx=(\ln x)(−\dfrac{1}{2}x^{−2})−∫(−\dfrac{1}{2}x^{−2})(\dfrac{1}{x}\,dx) \\[4pt] &=−\dfrac{1}{2}x^{−2}\ln x+∫\dfrac{1}{2}x^{−3}\,\,dx \\[4pt] &=−\dfrac{1}{2}x^{−2}\ln x−\dfrac{1}{4}x^{−2}+C\ \\[4pt] &=−\dfrac{1}{2x^2}\ln x−\dfrac{1}{4x^2}+C \end{align*} \nonumber \]
Évaluer\[∫x\ln x \,\,dx. \nonumber \]
- Allusion
-
Utilisez\(u=\ln x\) et\(dv=x\,\,dx\).
- Réponse
-
\[∫x\ln x \,\,dx=\dfrac{1}{2}x^2\ln x−\dfrac{1}{4}x^2+C \nonumber \]
Dans certains cas, comme dans les deux exemples suivants, il peut être nécessaire d'appliquer l'intégration par parties plusieurs fois.
Évaluer\[∫x^2e^{3x}\,dx. \nonumber \]
Solution
À l'aide de LIATE, choisissez\(u=x^2\) et\(dv=e^{3x}\,dx\). Ainsi,\(du=2x\,dx\) et\(v=∫e^{3x}\,dx=\left(\dfrac{1}{3}\right)e^{3x}\). Par conséquent,
- \(u=x^2\)
- \(du=2x\,dx\)
- \(dv=e^{3x}\,dx\)
- \(v=∫e^{3x}\,dx=\dfrac{1}{3}e^{3x}.\)
La substitution dans l'équation \ ref {IBP} produit
\[∫x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−∫\dfrac{2}{3}xe^{3x}\,dx. \label{3A.2} \]
Nous ne pouvons toujours pas intégrer\(∫\dfrac{2}{3}xe^{3x}\,dx\) directement, mais l'intégrale a désormais moins de pouvoir\(x\). Nous pouvons évaluer cette nouvelle intégrale en utilisant à nouveau l'intégration par pièces. Pour ce faire, choisissez
\[u=x \nonumber \]
et
\[dv=\dfrac{2}{3}e^{3x}\,dx. \nonumber \]
Ainsi,
\[du=\,dx \nonumber \]
et
\[v=∫\left(\dfrac{2}{3}\right)e^{3x}\,dx=\left(\dfrac{2}{9}\right)e^{3x}. \nonumber \]
Maintenant, nous avons
- \(u=x\)
- \(du=\,dx\)
- \(dv=\dfrac{2}{3}e^{3x}\,dx\)
- \(\displaystyle v=∫\dfrac{2}{3}e^{3x}\,dx=\dfrac{2}{9}e^{3x}.\)
La substitution dans l'équation \ ref {3A.2} donne
\[∫x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−\left(\dfrac{2}{9}xe^{3x}−∫\dfrac{2}{9}e^{3x}\,dx\right). \nonumber \]
Après avoir évalué et simplifié la dernière intégrale, nous obtenons
\[∫x^2e^{3x}\,dx=\dfrac{1}{3}x^2e^{3x}−\dfrac{2}{9}xe^{3x}+\dfrac{2}{27}e^{3x}+C. \nonumber \]
Évaluer
\[∫t^3e^{t^2}dt. \nonumber \]
Solution
Si nous utilisons une interprétation stricte du mnémotechnique LIATE pour faire notre choix de\(u\), nous nous retrouvons avec\(u=t^3\) et\(dv=e^{t^2}dt\). Malheureusement, ce choix ne fonctionnera pas car nous ne sommes pas en mesure d'évaluer\(∫e^{t^2}dt\). Cependant, puisque nous pouvons évaluer\(∫te^{t^2}\,dx\), nous pouvons essayer de choisir\(u=t^2\) et\(dv=te^{t^2}dt.\) avec ces choix, nous avons
- \(u=t^2\)
- \(du=2tdt\)
- \(dv=te^{t^2}dt\)
- \(v=∫te^{t^2}dt=\dfrac{1}{2}e^{t^2}.\)
Ainsi, nous obtenons
\[\begin{align*} ∫t^3e^{t^2}dt =\dfrac{1}{2}t^2e^{t^2}−∫\dfrac{1}{2}e^{t^2}2t\,dt \\[4pt] =\dfrac{1}{2}t^2e^{t^2}−\dfrac{1}{2}e^{t^2}+C. \end{align*}\]
Évaluer\[∫\sin (\ln x)\,dx. \nonumber \]
Solution
Cette intégrale semble n'avoir qu'une seule fonction, à savoir,\(\sin (\ln x)\) mais nous pouvons toujours utiliser la fonction constante 1 comme autre fonction. Dans cet exemple, choisissons\(u=\sin (\ln x)\) et\(dv=1\,dx\). (La décision d'utiliser\(u=\sin (\ln x)\) est facile. Nous ne pouvons pas choisir\(dv=\sin (\ln x)\,dx\) car si nous pouvions l'intégrer, nous n'utiliserions pas l'intégration par parties au départ !) Par conséquent,\(du=(1/x)\cos (\ln x) \,dx\) et\(v=∫ 1 \,dx=x.\) après avoir appliqué l'intégration par parties à l'intégrale et la simplification, nous avons
\[∫\sin \left(\ln x\right) \,dx=x \sin (\ln x)−\int \cos (\ln x)\,dx. \nonumber \]
Malheureusement, ce processus nous laisse une nouvelle intégrale très similaire à l'original. Voyons toutefois ce qui se passe lorsque nous appliquons à nouveau l'intégration par parties. Cette fois, choisissons\(u=\cos (\ln x)\) et\(dv=1\,dx,\) fabriquons\(du=−(1/x)\sin (\ln x)\,dx\) et\(v=∫1\,dx=x.\)
En remplacement, nous avons
\[∫\sin (\ln x)\,dx=x \sin (\ln x)−(x \cos (\ln x)-∫−\sin (\ln x)\,dx). \nonumber \]
Après avoir simplifié, nous obtenons
\[∫\sin (\ln x)\,dx=x\sin (\ln x)−x \cos (\ln x)−∫\sin (\ln x)\,dx. \nonumber \]
La dernière intégrale est désormais la même que l'intégrale originale. Il peut sembler que nous avons simplement fait un cercle, mais maintenant nous pouvons réellement évaluer l'intégrale. Pour voir comment procéder plus clairement, remplacez\(I=∫\sin (\ln x)\,dx.\) Ainsi, l'équation devient
\[I=x \sin (\ln x)−x \cos (\ln x)−I. \nonumber \]
Tout d'abord, ajoutez\(I\) les deux côtés de l'équation pour obtenir
\[2I=x \sin (\ln x)−x \cos (\ln x). \nonumber \]
Ensuite, divisez par 2 :
\[I=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x). \nonumber \]
En remplaçant\(I=∫\sin (\ln x)\,dx\) encore une fois, nous avons
\[ \int \sin (\ln x) \,dx=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x). \nonumber \]
De là, nous voyons que\((1/2)x \sin (\ln x)−(1/2)x \cos (\ln x)\) c'est un antidérivé de\(\sin (\ln x)\,dx\). Pour l'antidérivé le plus général, ajouter\(+C\) :
\[ ∫ \sin (\ln x) \,dx=\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x \cos (\ln x)+C. \nonumber \]
Analyse
Si cette méthode semble un peu étrange au début, on peut vérifier la réponse par différenciation :
\[\begin{align*} \dfrac{d}{\,dx}\left(\dfrac{1}{2}x \sin (\ln x)−\dfrac{1}{2}x\cos (\ln x)\right) \\[4pt] &=\dfrac{1}{2}(\sin (\ln x))+\cos (\ln x)⋅\dfrac{1}{x}⋅\dfrac{1}{2}x−\left(\dfrac{1}{2}\cos (\ln x)−\sin (\ln x)⋅\dfrac{1}{x}⋅\dfrac{1}{2}x\right) \\[4pt] &=\sin (\ln x). \end{align*}\]
Évaluer\[∫x^2\sin x\,dx. \nonumber \]
- Allusion
-
Ceci est similaire à Examples\(\PageIndex{3A}\) -\(\PageIndex{3C}\).
- Réponse
-
\[∫x^2\sin x\,dx=−x^2\cos x+2x\sin x+2\cos x+C \nonumber \]
Intégration par pièces pour des intégrales définies
Maintenant que nous avons utilisé l'intégration par parties avec succès pour évaluer des intégrales indéfinies, nous nous intéressons aux intégrales définies. La technique d'intégration est vraiment la même, mais nous ajoutons une étape pour évaluer l'intégrale aux limites supérieure et inférieure de l'intégration.
Fonctions\(u=f(x)\) Let and\(v=g(x)\) Be avec des dérivées continues sur [\(a,b\)]. Alors
\[∫^b_a u\,dv=uv\Big|^b_a−∫^b_a v\, du \nonumber \]
Détermine l'aire de la région délimitée au-dessus par le graphique de\(y=\tan^{−1}x\) et au-dessous par l'\(x\)axe -sur l'intervalle [\(0,1\)].
Solution
Cette région est illustrée dans la figure\(\PageIndex{1}\). Pour trouver la zone, il faut évaluer
\[∫^1_0 \tan^{−1}x\, \,dx. \nonumber \]
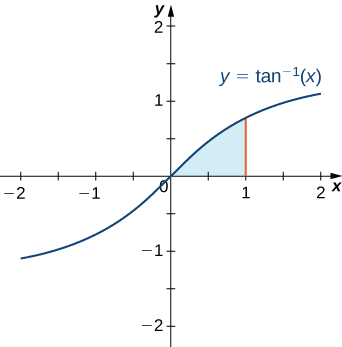
Pour cette intégrale, choisissons\(u=tan^{−1}x\) et\(dv=\,dx\), par conséquent, créons\(du=\dfrac{1}{x^2+1}\,dx\) et\(v=x\). Après avoir appliqué la formule d'intégration par parties (équation \ ref {IBP}), nous obtenons
\[ \text{Area}=\left. x \tan^{−1} x \right|^1_0−∫^1_0 \dfrac{x}{x^2+1} \,dx. \nonumber \]
Utilisez\(u\) -substitution pour obtenir
\[∫^1_0\dfrac{x}{x^2+1}\,dx=\left.\dfrac{1}{2}\ln \left(x^2+1\right) \right|^1_0. \nonumber \]
Ainsi,
\[\text{Area}=x \tan^{−1}x \Big|^1_0− \left.\dfrac{1}{2}\ln \left( x^2+1 \right) \right|^1_0=\left(\dfrac{π}{4}−\dfrac{1}{2}\ln 2\right) \,\text{units}^2. \nonumber \]
À ce stade, ce n'est peut-être pas une mauvaise idée de « vérifier la réalité » du caractère raisonnable de notre solution. Depuis\(\dfrac{π}{4}−\dfrac{1}{2}\ln 2≈0.4388\,\text{units}^2,\) et d'après la Figure,\(\PageIndex{1}\) nous nous attendons à ce que notre superficie soit légèrement inférieure à\(0.5\,\text{units}^2,\) ce que cette solution semble raisonnable.
Déterminez le volume du solide obtenu en faisant tourner la région délimitée par le graphe de\(f(x)=e^{−x},\) l'\(x\)axe -, de l'\(y\)axe -et de la droite\(x=1\) autour de l'\(y\)axe.
Solution
La meilleure solution pour résoudre ce problème est d'utiliser la méthode shell. Commencez par dessiner la région à faire pivoter, ainsi qu'un rectangle typique (Figure\(\PageIndex{2}\)).
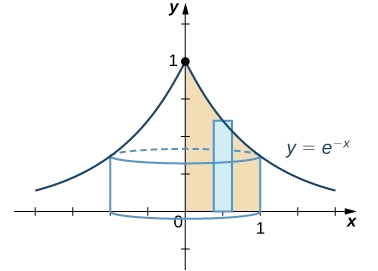
Pour trouver le volume à l'aide de coques, il faut évaluer
\[2π∫^1_0xe^{−x}\,dx. \label{4B.1} \]
Pour ce faire, laissez\(u=x\) et\(dv=e^{−x}\). Ces choix mènent à\(du=\,dx\) et\(v=∫e^{−x}\,dx=−e^{−x}.\) en utilisant la formule de la méthode Shell, nous obtenons
\ [\ begin {align*} \ text {Volume} &=2πο^1_0xe^ {−x} \, dx \ \ [4pt] = 2π \ left (−xe^ {−x} \ big|^1_0+^1_0E^ {−x} \, dx \ right) \ tag {Utiliser l'intégration par parties} \ \ [4pt]
&= 2π \ left (-e^ {-1} + 0 - e^ {-x} \ Big|^1_0 \ right) \ \ [4 points]
&= 2π \ left (-e^ {-1} - e^ {-1} + 1 \ right) \ \ [4 points]
&= 2π \ left (1 - \ dfrac {2} {e} \ right) \, \ text {unités} ^3. \ tag {Évaluer et simplifier} \ end {align*} \]
Analyse
Encore une fois, c'est une bonne idée de vérifier le caractère raisonnable de notre solution. Nous observons que le solide a un volume légèrement inférieur à celui d'un cylindre de rayon\(1\) et de hauteur de\(1/e\) ajouté au volume d'un cône de base, de rayon\(1\) et de hauteur de.\(1−\dfrac{1}{e}.\) Par conséquent, le solide doit avoir un volume un peu inférieur à
\[π(1)^2\dfrac{1}{e}+\left(\dfrac{π}{3}\right)(1)^2\left(1−\dfrac{1}{e}\right)=\dfrac{2π}{3e}+\dfrac{π}{3}≈1.8177\,\text{units}^3. \nonumber \]
Puisque\(2π−\dfrac{4π}{e}≈1.6603,\) nous voyons que notre volume calculé est raisonnable.
Évaluer\[∫^{π/2}_0x\cos x\,dx. \nonumber \]
- Allusion
-
Utilisez l'équation \ ref {IBP} avec\(u=x\) et\(dv=\cos x\,dx.\)
- Réponse
-
\[∫^{π/2}_0x\cos x\,dx = \dfrac{π}{2}−1 \nonumber \]
Concepts clés
- La formule d'intégration par parties (Équation \ ref {IBP}) permet l'échange d'une intégrale contre une autre intégrale, peut-être plus facile.
- L'intégration par parties s'applique à la fois aux intégrales définies et indéfinies.
Équations clés
- Formule d'intégration par pièces
\(\displaystyle ∫u\,dv=uv−∫v\,du\)
- Intégration par pièces pour des intégrales définies
\(\displaystyle ∫^b_au\,dv=uv\Big|^b_a−∫^b_av\,du\)
Lexique
- intégration par pièces
- une technique d'intégration qui permet l'échange d'une intégrale pour une autre à l'aide de la formule\(\displaystyle ∫u\,dv=uv−∫v\,du\)


