6.9 : Calcul des fonctions hyperboliques
- Page ID
- 197189
- Appliquez les formules pour les dérivées et les intégrales des fonctions hyperboliques.
- Appliquez les formules pour les dérivées des fonctions hyperboliques inverses et leurs intégrales associées.
- Décrire les conditions couramment appliquées à une courbe caténaire.
Nous avons déjà été initiés aux fonctions hyperboliques, ainsi qu'à certaines de leurs propriétés de base. Dans cette section, nous examinons les formules de différenciation et d'intégration pour les fonctions hyperboliques et leurs inverses.
Dérivées et intégrales des fonctions hyperboliques
Rappelons que le sinus hyperbolique et le cosinus hyperbolique sont définis comme
\[\sinh x=\dfrac{e^x−e^{−x}}{2} \nonumber \]
et
\[\cosh x=\dfrac{e^x+e^{−x}}{2}. \nonumber \]
Les autres fonctions hyperboliques sont ensuite définies en termes de\(\sinh x\) et\(\cosh x\). Les graphes des fonctions hyperboliques sont présentés dans la figure\(\PageIndex{1}\).
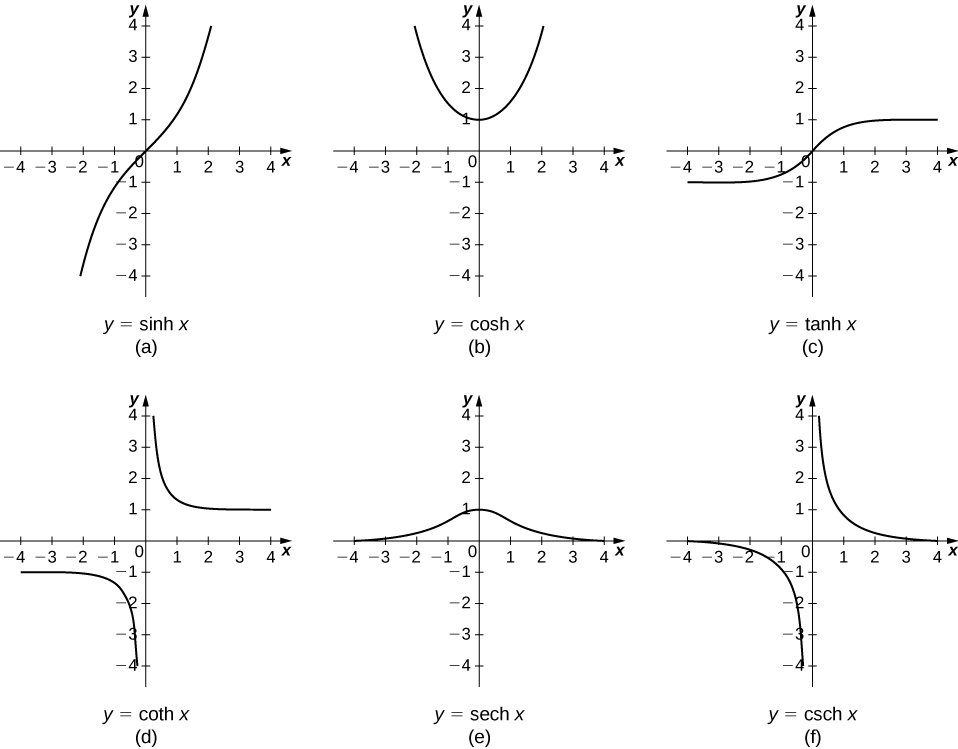
Il est facile de développer des formules de différenciation pour les fonctions hyperboliques. Par exemple, en regardant\(\sinh x\) que nous avons
\[\begin{align*} \dfrac{d}{dx} \left(\sinh x \right) &=\dfrac{d}{dx} \left(\dfrac{e^x−e^{−x}}{2}\right) \\[4pt] &=\dfrac{1}{2}\left[\dfrac{d}{dx}(e^x)−\dfrac{d}{dx}(e^{−x})\right] \\[4pt] &=\dfrac{1}{2}[e^x+e^{−x}] \\[4pt] &=\cosh x. \end{align*} \nonumber \]
De même,
\[\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]
Nous résumons les formules de différenciation pour les fonctions hyperboliques dans le tableau\(\PageIndex{1}\).
| \(f(x)\) | \(\dfrac{d}{dx}f(x)\) |
|---|---|
| \ (f (x) \) » style="text-align:center ; « >\(\sinh x\) | \ (\ dfrac {d} {dx} f (x) \) » style="text-align:center ; « >\(\cosh x\) |
| \ (f (x) \) » style="text-align:center ; « >\(\cosh x\) | \ (\ dfrac {d} {dx} f (x) \) » style="text-align:center ; « >\(\sinh x\) |
| \ (f (x) \) » style="text-align:center ; « >\(\tanh x\) | \ (\ dfrac {d} {dx} f (x) \) » style="text-align:center ; « >\(\text{sech}^2 \,x\) |
| \ (f (x) \) » style="text-align:center ; « >\(\text{coth } x\) | \ (\ dfrac {d} {dx} f (x) \) » style="text-align:center ; « >\(−\text{csch}^2\, x\) |
| \ (f (x) \) » style="text-align:center ; « >\(\text{sech } x\) | \ (\ dfrac {d} {dx} f (x) \) » style="text-align:center ; « >\(−\text{sech}\, x \tanh x\) |
| \ (f (x) \) » style="text-align:center ; « >\(\text{csch } x\) | \ (\ dfrac {d} {dx} f (x) \) » style="text-align:center ; « >\(−\text{csch}\, x \coth x\) |
Prenons un moment pour comparer les dérivées des fonctions hyperboliques avec les dérivées des fonctions trigonométriques standard. Il y a beaucoup de similitudes, mais aussi des différences. Par exemple, les dérivées des fonctions sinusoïdales correspondent à :
\[\dfrac{d}{dx} \sin x=\cos x \nonumber \]
et
\[\dfrac{d}{dx} \sinh x=\cosh x. \nonumber \]
Les dérivées des fonctions cosinusoïdales diffèrent cependant par leur signe :
\[\dfrac{d}{dx} \cos x=−\sin x, \nonumber \]
mais
\[\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]
Alors que nous poursuivons notre examen des fonctions hyperboliques, nous devons être conscients de leurs similitudes et de leurs différences avec les fonctions trigonométriques standard. Ces formules de différenciation pour les fonctions hyperboliques mènent directement aux formules intégrales suivantes.
\[ \begin{align} \int \sinh u \,du &=\cosh u+C \\[4pt] \int \text{csch}^2 u \, du &=−\coth u+C \\[4pt] \int \cosh u \,du &=\sinh u+C \\[4pt] \int \text{sech} \,u \tanh u \,du &=−\text{sech } \,u+C−\text{csch} \,u+C \\[4pt] \int \text{sech }^2u \,du &=\tanh u+C \\[4pt] \int \text{csch} \,u \coth u \,du &=−\text{csch} \,u+C \end{align} \nonumber \]
Évaluez les dérivés suivants :
- \(\dfrac{d}{dx}(\sinh(x^2))\)
- \(\dfrac{d}{dx}(\cosh x)^2\)
Solution :
En utilisant les formules du tableau\(\PageIndex{1}\) et la règle de chaîne, nous obtenons
- \(\dfrac{d}{dx}(\sinh(x^2))=\cosh(x^2)⋅2x\)
- \(\dfrac{d}{dx}(\cosh x)^2=2\cosh x\sinh x\)
Évaluez les dérivés suivants :
- \(\dfrac{d}{dx}(\tanh(x^2+3x))\)
- \(\dfrac{d}{dx}\left(\dfrac{1}{(\sinh x)^2}\right)\)
- Allusion
-
Utilisez les formules du tableau\(\PageIndex{1}\) et appliquez la règle de chaîne si nécessaire.
- Répondez à
-
\(\dfrac{d}{dx}(\tanh(x^2+3x))=(\text{sech}^2(x^2+3x))(2x+3)\)
- Réponse b
-
\(\dfrac{d}{dx}\left(\dfrac{1}{(\sinh x)^2}\right)=\dfrac{d}{dx}(\sinh x)^{−2}=−2(\sinh x)^{−3}\cosh x\)
Évaluez les intégrales suivantes :
- \( \displaystyle \int x\cosh(x^2)dx\)
- \( \displaystyle \int \tanh x\,dx\)
Solution
Nous pouvons utiliser\(u\) -substitution dans les deux cas.
a. Laissez\(u=x^2\). Ensuite,\(du=2x\,dx\) et
\[\begin{align*} \int x\cosh (x^2)dx &=\int \dfrac{1}{2}\cosh u\,du \\[4pt] &=\dfrac{1}{2}\sinh u+C \\[4pt] &=\dfrac{1}{2}\sinh (x^2)+C. \end{align*}\]
b. Laissez\(u=\cosh x\). Ensuite,\(du=\sinh x\,dx\) et
\[\begin{align*} \int \tanh x \,dx &=\int \dfrac{\sinh x}{\cosh x}\,dx \\[4pt] &=\int \dfrac{1}{u}du \\[4pt] &=\ln|u|+C \\[4pt] &= \ln|\cosh x|+C.\end{align*}\]
Notez que\(\cosh x>0\) pour tous\(x\), nous pouvons donc éliminer les signes de valeur absolue et obtenir
\[\int \tanh x \,dx=\ln(\cosh x)+C. \nonumber \]
Évaluez les intégrales suivantes :
- \(\displaystyle \int \sinh^3x \cosh x \,dx\)
- \(\displaystyle \int \text{sech }^2(3x)\, dx\)
- Allusion
-
Utilisez les formules ci-dessus et appliquez la\(u\) substitution si nécessaire.
- Répondez à
-
\(\displaystyle \int \sinh^3x \cosh x \,dx=\dfrac{\sinh^4x}{4}+C\)
- Réponse b
-
\(\displaystyle \int \text{sech }^2(3x) \, dx=\dfrac{\tanh(3x)}{3}+C\)
Calcul des fonctions hyperboliques inverses
En examinant les graphiques des fonctions hyperboliques, nous constatons qu'avec des restrictions de plage appropriées, elles ont toutes des inverses. La plupart des restrictions de portée nécessaires peuvent être discernées en examinant attentivement les graphiques. Les domaines et plages des fonctions hyperboliques inverses sont résumés dans le tableau\(\PageIndex{2}\).
| Fonction | Domaine | Gamme |
|---|---|---|
| \(\sinh^{−1}x\) | (−∞, ∞) | (−∞, ∞) |
| \(\cosh^{−1}x\) | (1, ∞) | [0, ∞) |
| \(\tanh^{−1}x\) | (−1,1) | (−∞, ∞) |
| \(\coth^{−1}x\) | (−∞, 1) (1, ∞) | (−,0) (0, ∞) |
| \(\text{sech}^{−1}x\) | (0,1) | [0, ∞) |
| \(\text{csch}^{−1}x\) | (−,0) (0, ∞) | (−,0) (0, ∞) |
Les graphes des fonctions hyperboliques inverses sont illustrés dans la figure suivante.
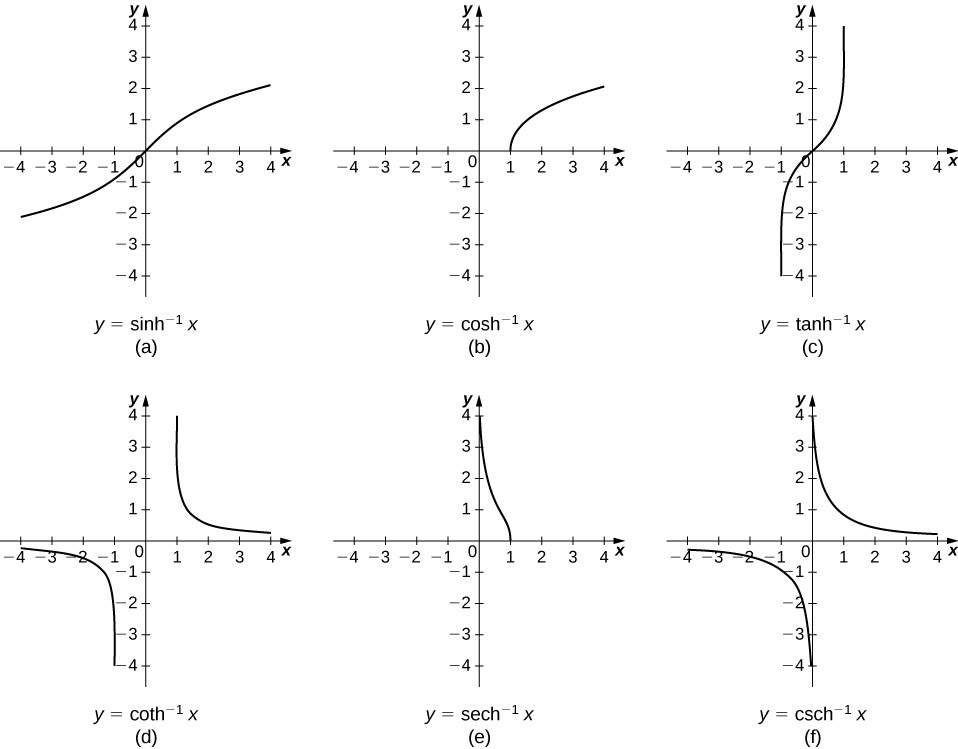
Pour trouver les dérivées des fonctions inverses, nous utilisons la différenciation implicite. Nous avons
\[\begin{align} y &=\sinh^{−1}x \\[4pt] \sinh y &=x \\[4pt] \dfrac{d}{dx} \sinh y &=\dfrac{d}{dx}x \\[4pt] \cosh y\dfrac{dy}{dx} &=1. \end{align} \nonumber \]
Souvenez-vous que\(\cosh^2y−\sinh^2y=1,\)\(\cosh y=\sqrt{1+\sinh^2y}\) oui. Ensuite,
\[\dfrac{dy}{dx}=\dfrac{1}{\cosh y}=\dfrac{1}{\sqrt{1+\sinh^2y}}=\dfrac{1}{\sqrt{1+x^2}}. \nonumber \]
Nous pouvons dériver des formules de différenciation pour les autres fonctions hyperboliques inverses de la même manière. Ces formules de différenciation sont résumées dans le tableau\(\PageIndex{3}\).
| \(f(x)\) | \(\dfrac{d}{dx}f(x)\) |
|---|---|
| \ (f (x) \) » style="vertical-align:middle ; « >\(\sinh^{−1}x\) | \ (\ dfrac {d} {dx} f (x) \) » style="vertical-align:middle ; « >\(\dfrac{1}{\sqrt{1+x^2}}\) |
| \ (f (x) \) » style="vertical-align:middle ; « >\(\cosh^{−1}x\) | \ (\ dfrac {d} {dx} f (x) \) » style="vertical-align:middle ; « >\(\dfrac{1}{\sqrt{x^2−1}}\) |
| \ (f (x) \) » style="vertical-align:middle ; « >\(\tanh^{−1}x\) | \ (\ dfrac {d} {dx} f (x) \) » style="vertical-align:middle ; « >\(\dfrac{1}{1−x^2}\) |
| \ (f (x) \) » style="vertical-align:middle ; « >\(\coth^{−1}x\) | \ (\ dfrac {d} {dx} f (x) \) » style="vertical-align:middle ; « >\(\dfrac{1}{1−x^2}\) |
| \ (f (x) \) » style="vertical-align:middle ; « >\(\text{sech}^{−1}x\) | \ (\ dfrac {d} {dx} f (x) \) » style="vertical-align:middle ; « >\(\dfrac{−1}{x\sqrt{1−x^2}}\) |
| \ (f (x) \) » style="vertical-align:middle ; « >\(\text{csch}^{−1}x\) | \ (\ dfrac {d} {dx} f (x) \) » style="vertical-align:middle ; « >\(\dfrac{−1}{|x|\sqrt{1+x^2}}\) |
Notez que les dérivés de\(\tanh^{−1}x\) et\(\coth^{−1}x\) sont les mêmes. Ainsi, lors de l'intégration\(1/(1−x^2)\), nous devons sélectionner l'antidérivé approprié en fonction du domaine des fonctions et des valeurs de\(x\). Les formules d'intégration impliquant les fonctions hyperboliques inverses sont résumées comme suit.
\[\int \dfrac{1}{\sqrt{1+u^2}}du=\sinh^{−1}u+C \nonumber \]
\[\int \dfrac{1}{u\sqrt{1−u^2}}du=−\text{sech}^{−1}|u|+C \nonumber \]
\[\int \dfrac{1}{\sqrt{u^2−1}}du=\cosh^{−1}u+C \nonumber \]
\[\int \dfrac{1}{u\sqrt{1+u^2}}du=−\text{csch}^{−1}|u|+C \nonumber \]
\[\int \dfrac{1}{1−u^2}du=\begin{cases}\tanh^{−1}u+C & \text{if }|u|<1\\ \coth^{−1}u+C & \text{if }|u|>1\end{cases} \nonumber \]
Évaluez les dérivés suivants :
- \(\dfrac{d}{dx}\left(\sinh^{−1}\left(\dfrac{x}{3}\right)\right)\)
- \(\dfrac{d}{dx}\left(\tanh^{−1}x\right)^2\)
Solution
En utilisant les formules du tableau\(\PageIndex{3}\) et la règle de chaîne, nous obtenons les résultats suivants :
- \(\dfrac{d}{dx}(\sinh^{−1}(\dfrac{x}{3}))=\dfrac{1}{3\sqrt{1+\dfrac{x^2}{9}}}=\dfrac{1}{\sqrt{9+x^2}}\)
- \(\dfrac{d}{dx}(\tanh^{−1}x)^2=\dfrac{2(\tanh^{−1}x)}{1−x^2}\)
Évaluez les dérivés suivants :
- \(\dfrac{d}{dx}(\cosh^{−1}(3x))\)
- \(\dfrac{d}{dx}(\coth^{−1}x)^3\)
- Allusion
-
Utilisez les formules du tableau\(\PageIndex{3}\) et appliquez la règle de chaîne si nécessaire.
- Répondez à
-
\(\dfrac{d}{dx}(\cosh^{−1}(3x))=\dfrac{3}{\sqrt{9x^2−1}} \)
- Réponse b
-
\(\dfrac{d}{dx}(\coth^{−1}x)^3=\dfrac{3(\coth^{−1}x)^2}{1−x^2} \)
Évaluez les intégrales suivantes :
- \(\displaystyle \int \dfrac{1}{\sqrt{4x^2−1}}dx\)
- \(\displaystyle \int \dfrac{1}{2x\sqrt{1−9x^2}}dx\)
Solution
Nous pouvons utiliser \(u\)-substitution dans les deux cas.
Laissez\(u=2x\). Ensuite,\(du=2\,dx\) et nous avons
\[\begin{align*} \int \dfrac{1}{\sqrt{4x^2−1}}\,dx &=\int \dfrac{1}{2\sqrt{u^2−1}}\,du \\[4pt] &=\dfrac{1}{2}\cosh^{−1}u+C \\[4pt] &=\dfrac{1}{2}\cosh^{−1}(2x)+C. \end{align*} \nonumber \]
Laissez\(u=3x.\) ensuite,\(du=3\,dx\) et nous obtenons
\[\begin{align*} \int \dfrac{1}{2x\sqrt{1−9x^2}}dx &=\dfrac{1}{2}\int \dfrac{1}{u\sqrt{1−u^2}}du \\[4pt] &=−\dfrac{1}{2}\text{sech}^{−1}|u|+C \\[4pt] &=−\dfrac{1}{2}\text{sech}^{−1}|3x|+C \end{align*}\]
Évaluez les intégrales suivantes :
- \(\displaystyle \int \dfrac{1}{\sqrt{x^2−4}}dx,x>2\)
- \(\displaystyle \int \dfrac{1}{\sqrt{1−e^{2x}}}dx\)
- Allusion
-
Utilisez les formules ci-dessus et appliquez la\(u\) substitution si nécessaire.
- Répondez à
-
\(\displaystyle \int \dfrac{1}{\sqrt{x^2−4}}dx=\cosh^{−1}(\dfrac{x}{2})+C\)
- Réponse b
-
\( \displaystyle \int \dfrac{1}{\sqrt{1−e^{2x}}}dx=−\text{sech}^{−1}(e^x)+C\)
Applications
L'une des applications physiques des fonctions hyperboliques consiste à suspendre des câbles. Si un câble de densité uniforme est suspendu entre deux supports sans aucune charge autre que son propre poids, le câble forme une courbe appelée caténaire. Les lignes à haute tension, les chaînes suspendues entre deux poteaux et les torons d'une toile d'araignée forment tous des caténaires. La figure suivante montre des chaînes suspendues à une rangée de poteaux.

Les fonctions hyperboliques peuvent être utilisées pour modéliser des caténaires. Plus précisément, les fonctions du formulaire\(y=a\cdot \cosh(x/a)\) sont des caténaires. La figure\(\PageIndex{4}\) montre le graphique de\(y=2\cosh(x/2)\).
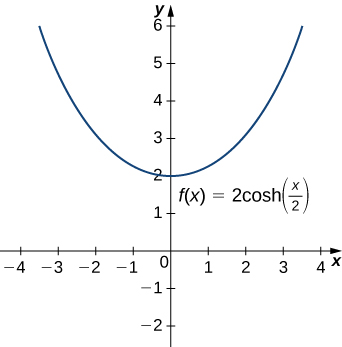
Supposons qu'un câble suspendu ait la forme\(10\cosh(x/10)\) de\(−15≤x≤15\), où\(x\) est mesuré en pieds. Déterminez la longueur du câble (en pieds).
Solution
Rappelons que dans la section 6.4, la formule pour la longueur de l'arc est
\[\underbrace{\int ^b_a\sqrt{1+[f′(x)]^2}dx}_{\text{Arc Length}}. \nonumber \]
Nous l'avons fait\(f(x)=10 \cosh(x/10)\), donc\(f′(x)=\sinh(x/10)\). Ensuite, la longueur de l'arc est
\[\int ^b_a\sqrt{1+[f′(x)]^2}dx=\int ^{15}_{−15}\sqrt{1+\sinh^2 \left(\dfrac{x}{10}\right)}dx. \nonumber \]
Maintenant, rappelez-vous que
\[1+\sinh^2x=\cosh^2x, \nonumber \]
nous avons donc
\[\begin{align*} \text{Arc Length} &= \int ^{15}_{−15}\sqrt{1+\sinh^2 \left(\dfrac{x}{10}\right)}dx \\[4pt] &=\int ^{15}_{−15}\cosh \left(\dfrac{x}{10}\right)dx \\[4pt] &= \left.10\sinh \left(\dfrac{x}{10}\right)\right|^{15}_{−15}\\[4pt] &=10\left[\sinh\left(\dfrac{3}{2}\right)−\sinh\left(−\dfrac{3}{2}\right)\right]\\[4pt] &=20\sinh \left(\dfrac{3}{2}\right) \\[4pt] &≈42.586\,\text{ft.} \end{align*}\]
Supposons qu'un câble suspendu ait la forme\(15 \cosh (x/15)\) de\(−20≤x≤20\). Déterminez la longueur du câble (en pieds).
- Réponse
-
\(52.95\)pieds
Concepts clés
- Les fonctions hyperboliques sont définies en termes de fonctions exponentielles.
- La différenciation terme par terme fournit des formules de différenciation pour les fonctions hyperboliques. Ces formules de différenciation donnent lieu, à leur tour, à des formules d'intégration.
- Avec des restrictions de portée appropriées, les fonctions hyperboliques ont toutes des inverses.
- La différenciation implicite produit des formules de différenciation pour les fonctions hyperboliques inverses, qui à leur tour donnent lieu à des formules d'intégration.
- Les applications physiques les plus courantes des fonctions hyperboliques sont les calculs impliquant des caténaires.
Lexique
- caténaire
- une courbe ayant la forme de la fonction\(y=a\cdot\cosh(x/a)\) est une caténaire ; un câble de densité uniforme suspendu entre deux supports prend la forme d'une caténaire


