6.8 : Croissance et décroissance exponentielles
- Page ID
- 197231
- Utilisez le modèle de croissance exponentielle dans des applications, notamment pour la croissance démographique et les intérêts composés.
- Expliquez le concept du doublement du temps.
- Utilisez le modèle de désintégration exponentielle dans des applications, notamment la désintégration radioactive et la loi de Newton sur le refroidissement.
- Expliquez le concept de demi-vie.
L'une des applications les plus courantes des fonctions exponentielles concerne les modèles de croissance et de décroissance. La croissance et la décroissance exponentielles se manifestent dans de nombreuses applications naturelles. Qu'il s'agisse de la croissance démographique et de l'intérêt croissant continu, de la désintégration radioactive et de la loi de refroidissement de Newton, les fonctions exponentielles sont omniprésentes dans la nature. Dans cette section, nous examinons la croissance et la décroissance exponentielles dans le contexte de certaines de ces applications.
Modèle de croissance exponentielle
De nombreux systèmes connaissent une croissance exponentielle. Ces systèmes suivent un modèle de forme\(y=y_0e^{kt},\) où\(y_0\) représente l'état initial du système et\(k\) est une constante positive, appelée constante de croissance. Notez que dans un modèle de croissance exponentielle, nous avons
\[ y′=ky_0e^{kt}=ky. \label{eq1} \]
C'est-à-dire que le taux de croissance est proportionnel à la valeur de la fonction actuelle. Il s'agit là d'une caractéristique essentielle de la croissance exponentielle. L'équation \ ref {eq1} implique des dérivées et est appelée équation différentielle.
Les systèmes qui présentent une croissance exponentielle augmentent selon le modèle mathématique
\[y=y_0e^{kt} \nonumber \]
où\(y_0\) représente l'état initial du système et\(k>0\) est une constante, appelée constante de croissance.
La croissance démographique est un exemple courant de croissance exponentielle. Prenons l'exemple d'une population de bactéries. Il semble plausible que le taux de croissance démographique soit proportionnel à la taille de la population. Après tout, plus il y a de bactéries à reproduire, plus la population croît rapidement. La figure\(\PageIndex{1}\) et le tableau\(\PageIndex{1}\) représentent la croissance d'une population de bactéries avec une population initiale de 200 bactéries et une constante de croissance de 0,02. Remarquez qu'après seulement 2 heures (120 minutes), la population est 10 fois plus nombreuse qu'à l'origine !
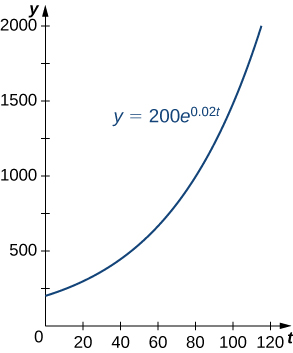
| Durée (min) | Taille de la population (nombre de bactéries) |
|---|---|
| 10 | 244 |
| 20 | 298 |
| 30 | 364 |
| 40 | 445 |
| 50 | 544 |
| 60 | 664 |
| 70 | 811 |
| 80 | 991 |
| 90 | 1210 |
| 100 | 1478 |
| 110 | 1805 |
| 120 | 2205 |
Notez que nous utilisons une fonction continue pour modéliser ce qui est un comportement intrinsèquement discret. À tout moment, la population réelle contient un grand nombre de bactéries, bien que le modèle prenne des valeurs non entières. Lorsque vous utilisez des modèles de croissance exponentielle, nous devons toujours être attentifs à interpréter les valeurs des fonctions dans le contexte du phénomène que nous modélisons.
Considérez la population de bactéries décrite précédemment. Cette population croît selon la fonction\(f(t)=200e^{0.02t},\) où t est mesuré en minutes. Combien de bactéries sont présentes dans la population après quelques\(5\) heures (\(300\)minutes) ? Quand la population atteint-elle\(100,000\) les bactéries ?
Solution
Nous avons\(f(t)=200e^{0.02t}.\) alors
\[ f(300)=200e^{0.02(300)}≈80,686. \nonumber \]
Il y a\(80,686\) des bactéries dans la population après les\(5\) heures de travail.
Pour savoir quand la population atteint\(100,000\) les bactéries, nous résolvons l'équation
\[ \begin{align*} 100,000 &= 200e^{0.02t} \\[4pt] 500 &=e^{0.02t} \\[4pt] \ln 500 &=0.02 t \\[4pt] t &=\frac{\ln 500}{0.02}≈310.73. \end{align*} \nonumber \]
La population atteint\(100,000\) les bactéries au bout de\(310.73\) quelques minutes.
Prenons l'exemple d'une population de bactéries qui croît en fonction de la fonction\(f(t)=500e^{0.05t}\), mesurée en minutes.\(t\) Combien de bactéries sont présentes dans la population après 4 heures ? Quand est-ce que la population atteindra le\(100\) million de bactéries ?
- Réponse
-
Utilisez le processus de l'exemple précédent.
- Réponse
-
Il y a\(81,377,396\) des bactéries dans la population après les\(4\) heures de travail. La population atteint un\(100\) million de bactéries en\(244.12\) quelques minutes.
Passons maintenant à une application financière : les intérêts composés. L'intérêt qui n'est pas composé est appelé intérêt simple. Les intérêts simples sont payés une seule fois, à la fin de la période spécifiée (généralement une\(1\) année). Donc, si nous créons un compte d'épargne générant des intérêts\(2%\) simples par an, alors à la fin de l'année, nous avons\($1000\)
\[ 1000(1+0.02)=$1020. \nonumber \]
Les intérêts composés sont payés plusieurs fois par an, selon la période de composition. Par conséquent, si la banque compose les intérêts tous les\(6\) mois, elle crédite la moitié des intérêts de l'année sur le compte au bout de\(6\) plusieurs mois. Au cours du second semestre, le compte génère des intérêts non seulement sur les intérêts initiaux\($1000\), mais également sur les intérêts perçus au cours du premier semestre de l'année. Mathématiquement parlant, à la fin de l'année, nous avons
\[ 1000 \left(1+\dfrac{0.02}{2}\right)^2=$1020.10. \nonumber \]
De même, si l'intérêt est composé tous les\(4\) mois, nous avons
\[ 1000 \left(1+\dfrac{0.02}{3}\right)^3=$1020.13, \nonumber \]
et si l'intérêt est composé quotidiennement (\(365\)fois par an), c'est fait\($1020.20\). Si nous étendons ce concept, de manière à ce que l'intérêt soit continuellement aggravé, après des\(t\) années, nous avons
\[ 1000\lim_{n→∞} \left(1+\dfrac{0.02}{n}\right)^{nt}. \nonumber \]
Manipulons maintenant cette expression pour obtenir une fonction de croissance exponentielle. Rappelons que le nombre\(e\) peut être exprimé sous forme de limite :
\[ e=\lim_{m→∞}\left(1+\dfrac{1}{m}\right)^m. \nonumber \]
Sur cette base, nous voulons que l'expression entre parenthèses ait la forme\((1+1/m)\). Laissez\(n=0.02m\). Notez cela\(n→∞, m→∞\) également. Ensuite, nous obtenons
\[ 1000\lim_{n→∞}\left(1+\dfrac{0.02}{n}\right)^{nt}=1000\lim_{m→∞}\left(1+\dfrac{0.02}{0.02m}\right)^{0.02mt}=1000\left[\lim_{m→∞}\left(1+\dfrac{1}{m}\right)^m\right]^{0.02t}. \nonumber \]
Nous reconnaissons que la limite entre crochets est le nombre\(e\). Ainsi, le solde de notre compte bancaire après des\(t\) années est donné par\(1000 e^{0.02t}\). En généralisant ce concept, nous constatons que si un compte bancaire dont le solde initial\($P\) rapporte des intérêts à un taux de\(r%\), composé continuellement, alors le solde du compte après des\(t\) années est
\[ \text{Balance}\;=Pe^{rt}. \nonumber \]
Un étudiant de 25 ans a la possibilité d'investir de l'argent dans un compte de retraite qui verse des intérêts\(5%\) annuels composés en continu. Combien l'étudiante doit-elle investir aujourd'hui pour avoir un\($1\) million lorsqu'elle prendra sa retraite à l'âge de la retraite\(65\) ? Et si elle pouvait plutôt gagner des intérêts\(6%\) annuels composés de façon continue ?
Solution
Nous avons
\[ 1,000,000=Pe^{0.05(40)} \nonumber \]
\[ P=135,335.28. \nonumber \]
Elle doit investir\($135,335.28\) à\(5%\) taux d'intérêt.
Si, au contraire, elle est capable de gagner\(6%,\), l'équation devient
\[ 1,000,000=Pe^{0.06(40)} \nonumber \]
\[ P=90,717.95. \nonumber \]
Dans ce cas, elle n'a besoin que d'investir.\($90,717.95.\) Cela représente environ les deux tiers du montant dans lequel elle doit investir\(5%\). Le fait que l'intérêt soit composé en permanence amplifie considérablement l'effet de la\(1%\) hausse du taux d'intérêt.
Supposons qu'au lieu d'investir à l'âge\(25\sqrt{b^2−4ac}\), l'étudiant attend jusqu'à l'âge\(35\). Dans quel montant devrait-elle investir\(5%\) ? À\(6%\) ?
- Allusion
-
Utilisez le processus de l'exemple précédent.
- Réponse
-
À\(5%\) intérêt, elle doit investir\($223,130.16\). À\(6%\) intérêt, elle doit investir\($165,298.89.\)
Si une quantité croît de façon exponentielle, le temps nécessaire pour que la quantité double reste constant. En d'autres termes, il faut autant de temps à une population de bactéries pour passer d'une\(200\) bactérie\(100\) à une bactérie qu'\(10,000\)à une\(20,000\) bactérie. Ce temps s'appelle le temps de doublement. Pour calculer le temps de doublement, nous voulons savoir quand la quantité atteint le double de sa taille d'origine. Nous avons donc
\[ \begin{align*} 2y_0 &=y_0e^{kt} \\[4pt] 2 &=e^{kt} \\[4pt] \ln 2 &=kt \\[4pt] t &=\dfrac{\ln 2}{k}. \end{align*} \nonumber \]
Si une quantité croît de façon exponentielle, le temps de doublement est le temps qu'il faut à la quantité pour doubler. Il est donné par
\[\text{Doubling time}=\dfrac{\ln 2}{k}. \nonumber \]
Supposons qu'une population de poissons croît de façon exponentielle. Un étang est d'abord approvisionné en\(500\) poissons. Après des\(6\) mois, il y a\(1000\) des poissons dans l'étang. Le propriétaire autorisera ses amis et voisins à pêcher sur son étang une fois la population de poissons atteinte\(10,000\). Quand les amis du propriétaire seront-ils autorisés à pêcher ?
Solution
Nous savons qu'il faut des\(6\) mois à la population de poissons pour doubler. Donc, si cela\(t\) représente le temps en mois, selon la formule du doublement du temps, nous avons\(6=(\ln 2)/k\). Ensuite,\(k=(\ln 2)/6\). Ainsi, la population est donnée par\(y=500e^{((\ln 2)/6)t}\). Pour déterminer à quel moment la population atteint\(10,000\) les poissons, nous devons résoudre l'équation suivante :
\[ \begin{align*} 10,000 &=500e^{(\ln 2/6)t} \\[4pt] 20 &=e^{(\ln 2/6)t} \\[4pt] \ln 20 &=\left(\frac{\ln 2}{6}\right)t \\[4pt] t &=\frac{6(\ln 20)}{\ln 2} \\[4pt] &≈25.93. \end{align*} \nonumber \]
Les amis du propriétaire doivent attendre des\(25.93\) mois (un peu plus que des\(2\) années) pour pêcher dans l'étang.
Supposons qu'il faille des\(9\) mois pour que la population de poissons\(\PageIndex{3}\) de Example atteigne des\(1000\) poissons. Dans ces circonstances, combien de temps les amis du propriétaire doivent-ils attendre ?
- Allusion
-
Utilisez le processus de l'exemple précédent.
- Réponse
-
\(38.90\)mois
Modèle de décroissance exponentielle
Les fonctions exponentielles peuvent également être utilisées pour modéliser des populations qui diminuent (à cause d'une maladie, par exemple) ou des composés chimiques qui se décomposent au fil du temps. Nous disons que ces systèmes présentent une décroissance exponentielle plutôt qu'une croissance exponentielle. Le modèle est quasiment le même, sauf qu'il y a un signe négatif dans l'exposant. Ainsi, pour une constante positive\(k\), nous avons
\[ y=y_0e^{−kt}. \nonumber \]
Comme pour la croissance exponentielle, il existe une équation différentielle associée à la décroissance exponentielle. Nous avons
\[ y′=−ky_0e^{−kt}=−ky. \nonumber \]
Les systèmes qui présentent une décroissance exponentielle se comportent selon le modèle
\[y=y_0e^{−kt}, \nonumber \]
où\(y_0\) représente l'état initial du système et\(k>0\) est une constante, appelée constante de désintégration.
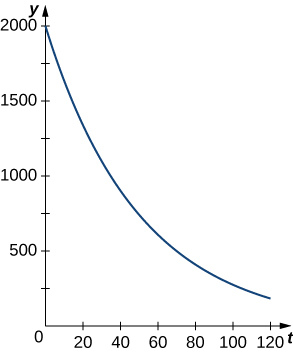
La figure\(\PageIndex{2}\) montre un graphique d'une fonction de décroissance exponentielle représentative.
Examinons une application physique de la décroissance exponentielle. La loi de Newton sur le refroidissement indique qu'un objet se refroidit à une vitesse proportionnelle à la différence entre la température de l'objet et la température de l'environnement. En d'autres termes, si\(T\) représente la température de l'objet et\(T_a\) représente la température ambiante dans une pièce, alors
\[T′=−k(T−T_a). \nonumber \]
Notez que ce n'est pas tout à fait le bon modèle pour la décroissance exponentielle. Nous voulons que la dérivée soit proportionnelle à la fonction, et cette expression comporte un\(T_a\) terme supplémentaire. Heureusement, nous pouvons modifier les variables pour résoudre ce problème. Laissez\(y(t)=T(t)−T_a\). Ensuite\(y′(t)=T′(t)−0=T′(t)\), et notre équation devient
\[ y′=−ky. \nonumber \]
D'après nos travaux antérieurs, nous savons que cette relation entre\(y\) et sa dérivée entraîne une décroissance exponentielle. Ainsi,
\[ y=y_0e^{−kt}, \nonumber \]
et nous voyons que
\[ T−T_a=(T_0−T_a)e^{−kt} \nonumber \]
\[ T=(T_0−T_a)e^{−kt}+T_a \nonumber \]
où\(T_0\) représente la température initiale. Appliquons cette formule dans l'exemple suivant.
Selon des baristas expérimentés, la température optimale pour servir le café se situe entre\(155°F\) et\(175°F\). Supposons que le café soit versé à une température de\(200°F\), et après\(2\) quelques minutes dans une\(70°F\) pièce, il ait refroidi\(180°F\). Quand le café est-il suffisamment frais pour être servi pour la première fois ? Quand est-ce que le café est trop froid pour être servi ? Arrondissez les réponses à la demi-minute la plus proche.
Solution
Nous avons
\[ \begin{align*} T &=(T_0−T_a)e^{−kt}+T_a \\[4pt] 180 &=(200−70)e^{−k(2)}+70 \\[4pt] 110 &=130e^{−2k} \\[4pt] \dfrac{11}{13} &=e^{−2k} \\[4pt] \ln \dfrac{11}{13} &=−2k \\[4pt] \ln 11−\ln 13 &=−2k \\[4pt] k &=\dfrac{\ln 13−\ln 11}{2} \end{align*}\]
Ensuite, le modèle est
\[T=130e^{(\ln 11−\ln 13/2)t}+70. \nonumber \]
Le café atteint\(175°F\) quand
\[ \begin{align*} 175 &=130e^{(\ln 11−\ln 13/2)t}+70 \\[4pt]105 &=130e^{(\ln 11−\ln 13/2)t} \\[4pt] \dfrac{21}{26} &=e^{(\ln 11−\ln 13/2)t} \\[4pt] \ln \dfrac{21}{26} &=\dfrac{\ln 11−\ln 13}{2}t \\[4pt] \ln 21−\ln 26 &=\left(\dfrac{\ln 11−\ln 13}{2}\right)t \\[4pt] t &=\dfrac{2(\ln 21−\ln 26)}{\ln 11−\ln 13}\\[4pt] &≈2.56. \end{align*}\]
Le café peut être servi quelques\(2.5\) minutes après avoir été versé. Le café\(155°F\) atteint
\[ \begin{align*} 155 &=130e^{(\ln 11−\ln 13/2)t}+70 \\[4pt] 85 &=130e^{(\ln 11−\ln 13)t} \\[4pt] \dfrac{17}{26} &=e^{(\ln 11−\ln 13)t} \\[4pt] \ln 17−\ln 26 &=\left(\dfrac{\ln 11−\ln 13}{2}\right)t \\[4pt] t &=\dfrac{2(\ln 17−\ln 26)}{\ln 11−\ln 13} \\[4pt] &≈5.09.\end{align*}\]
Le café est trop froid pour être servi quelques\(5\) minutes après avoir été versé.
Supposons que la pièce soit plus chaude\((75°F)\) et qu'au bout de\(2\) quelques minutes, le café soit refroidi uniquement à\(185°F.\) Quand le café est-il suffisamment froid pour être servi pour la première fois ? Quand est-ce que le café doit être trop froid pour être servi ? Arrondissez les réponses à la demi-minute la plus proche.
- Allusion
-
Utilisez le processus de l'exemple précédent.
- Réponse
-
Le café est d'abord suffisamment froid pour être servi environ\(3.5\) quelques minutes après avoir été versé. Le café est trop froid pour être servi quelques\(7\) minutes après avoir été versé.
Tout comme les systèmes présentant une croissance exponentielle ont un temps de doublement constant, les systèmes présentant une décroissance exponentielle ont une demi-vie constante. Pour calculer la demi-vie, nous voulons savoir quand la quantité atteint la moitié de sa taille initiale. Par conséquent, nous avons
\(\dfrac{y_0}{2}=y_0e^{−kt}\)
\(\dfrac{1}{2}=e^{−kt}\)
\(−\ln 2=−kt\)
\(t=\dfrac{\ln 2}{k}\).
Remarque : Il s'agit de la même expression que celle que nous avons trouvée pour doubler le temps.
Si une quantité diminue de façon exponentielle, la demi-vie est le temps qu'il faut à la quantité pour être réduite de moitié. Il est donné par
\[\text{Half-life}=\dfrac{\ln 2}{k}. \nonumber \]
L'une des applications les plus courantes d'un modèle de décroissance exponentielle est la datation au carbone. Le carbone 14 se désintègre (émet une particule radioactive) à un rythme exponentiel régulier et constant. Par conséquent, si nous savons quelle quantité de carbone 14 était initialement présente dans un objet et quelle quantité de carbone 14 reste, nous pouvons déterminer l'âge de l'objet. La demi-vie du carbone 14 est d'environ 5 730 ans, ce qui signifie qu'après ces nombreuses années, la moitié du matériau est passée du carbone 14 d'origine au nouvel azote 14 non radioactif. Si nous avons 100 g de carbone 14 aujourd'hui, combien en reste-t-il dans 50 ans ? Si un artefact qui contenait à l'origine 100 g de carbone 14 contient maintenant 10 g de carbone 14, quel âge a-t-il ? Arrondissez la réponse à la centaine d'années la plus proche.
Solution
Nous avons
\[ 5730=\dfrac{\ln 2}{k} \nonumber \]
\[ k=\dfrac{\ln 2}{5730}.\nonumber \]
Donc, le modèle dit
\[ y=100e^{−(\ln 2/5730)t}.\nonumber \]
\(50\)Depuis des années, nous avons
\[y=100e^{−(\ln 2/5730)(50)}≈99.40\nonumber \]
Par conséquent, au\(50\) fil des années, il reste 1\(99.40\) g de carbone 14.
Pour déterminer l'âge de l'artefact, nous devons résoudre
\[ \begin{align*} 10 &=100e^{−(\ln 2/5730)t} \\[4pt] \dfrac{1}{10} &= e^{−(\ln 2/5730)t} \\ t &≈19035. \end{align*}\]
L'artefact a environ des\(19,000\) années.
Si nous avons 100 g de carbone 14 , combien reste-t-il ? après 500 ans ? Si un artefact qui contenait à l'origine 100 g de carbone 14 en contient maintenant 20 g de carbone 14, quel âge a-t-il ? Arrondissez la réponse à la centaine d'années la plus proche.
- Allusion
-
Utilisez le processus de l'exemple précédent.
- Réponse
-
Il reste au total 94,13 g de carbone 14 après 500 ans. L'artefact a environ 13 300 ans.
Concepts clés
- La croissance exponentielle et la décroissance exponentielle sont deux des applications les plus courantes des fonctions exponentielles.
- Les systèmes qui présentent une croissance exponentielle suivent un modèle de la forme\(y=y_0e^{kt}\).
- En croissance exponentielle, le taux de croissance est proportionnel à la quantité présente. En d'autres termes,\(y′=ky\).
- Les systèmes qui présentent une croissance exponentielle ont un temps de doublement constant, qui est donné par\((\ln 2)/k\).
- Les systèmes qui présentent une décroissance exponentielle suivent un modèle de la forme\(y=y_0e^{−kt}.\)
- Les systèmes qui présentent une décroissance exponentielle ont une demi-vie constante, qui est donnée par\((\ln 2)/k.\)
Lexique
- temps de doublement
- si une quantité croît de façon exponentielle, le temps de doublement est le temps qu'il faut à la quantité pour doubler, et est donné par\((\ln 2)/k\)
- décroissance exponentielle
- les systèmes qui présentent une décroissance exponentielle suivent un modèle de la forme\(y=y_0e^{−kt}\)
- croissance exponentielle
- les systèmes qui présentent une croissance exponentielle suivent un modèle de la forme\(y=y_0e^{kt}\)
- demi-vie
- si une quantité décroît de façon exponentielle, la demi-vie est le temps qu'il faut à la quantité pour être réduite de moitié. Il est donné par\((\ln 2)/k\)


