6.7 : Intégrales, fonctions exponentielles et logarithmes
- Page ID
- 197230
- Écrivez la définition du logarithme naturel sous forme d'intégrale.
- Reconnaissez la dérivée du logarithme naturel.
- Intégrez des fonctions impliquant la fonction logarithmique naturelle.
- Définissez le nombre\(e\) à l'aide d'une intégrale.
- Reconnaissez la dérivée et l'intégrale de la fonction exponentielle.
- Prouvez les propriétés des logarithmes et des fonctions exponentielles à l'aide d'intégrales.
- Exprime les fonctions logarithmiques et exponentielles générales en termes de logarithmes naturels et d'exponentielles.
Nous avons déjà examiné les fonctions exponentielles et les logarithmes dans les chapitres précédents. Nous avons toutefois passé sous silence certains détails essentiels lors des discussions précédentes. Par exemple, nous n'avons pas étudié comment traiter les fonctions exponentielles avec des exposants irrationnels. La définition du nombre e est un autre domaine dans lequel le développement précédent était quelque peu incomplet. Nous disposons désormais des outils nécessaires pour traiter ces concepts d'une manière plus rigoureuse sur le plan mathématique, et nous le faisons dans cette section.
Pour les besoins de cette section, supposons que nous n'avons pas encore défini le logarithme naturel\(e\), le nombre ou aucune des formules d'intégration et de différenciation associées à ces fonctions. À la fin de la section, nous aurons étudié ces concepts d'une manière mathématiquement rigoureuse (et nous verrons qu'ils sont cohérents avec les concepts que nous avons appris plus tôt). Nous commençons la section en définissant le logarithme naturel en termes d'intégrale. Cette définition constitue le fondement de la section. À partir de cette définition, nous dérivons des formules de différenciation, définissons le nombre\(e\) et étendons ces concepts aux logarithmes et aux fonctions exponentielles de n'importe quelle base.
Le logarithme naturel en tant qu'intégrale
Rappelez-vous la règle de puissance pour les intégrales :
\[ ∫ x^n \,dx = \dfrac{x^{n+1}}{n+1} + C , \quad n≠−1. \nonumber \]
De toute évidence, cela ne fonctionne pas si\(n=−1,\) cela nous obligerait à diviser par zéro. Alors, qu'est-ce qu'on en fait\(\displaystyle ∫\dfrac{1}{x}\,dx\) ? Rappelons du théorème fondamental du calcul qui\(\displaystyle ∫^x_1\dfrac{1}{t}dt\) est un antidérivé de\(\dfrac{1}{x}.\) Par conséquent, nous pouvons faire la définition suivante.
Pour\(x>0\), définissez la fonction du logarithme naturel en utilisant
\[\ln x=∫^x_1\dfrac{1}{t}\,dt. \nonumber \]
\(x>1\)En effet, il s'agit simplement de la zone située sous la courbe\(y=\dfrac{1}{t}\) de\(1\) à\(x\). Pour\(x<1\), nous avons
\[ ∫^x_1\dfrac{1}{t}\,dt=−∫^1_x\dfrac{1}{t}\,dt, \nonumber \]
donc dans ce cas, c'est le négatif de l'aire sous la courbe de\(x\) à\(1\) (voir la figure suivante).
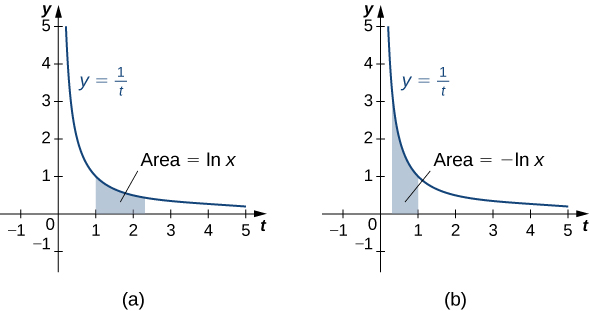
Remarquez que\(\ln 1=0\). En outre, la fonction\(y=\dfrac{1}{t}>0\) pour\(x>0\). Par conséquent, d'après les propriétés des intégrales, il est clair que cela\(\ln x\) augmente pour\(x>0\).
Propriétés du logarithme naturel
En raison de la façon dont nous avons défini le logarithme naturel, la formule de différenciation suivante disparaît immédiatement en raison du théorème fondamental du calcul.
Car\(x>0\), la dérivée du logarithme naturel est donnée par
\[ \dfrac{d}{dx}\Big( \ln x \Big) = \dfrac{1}{x}. \nonumber \]
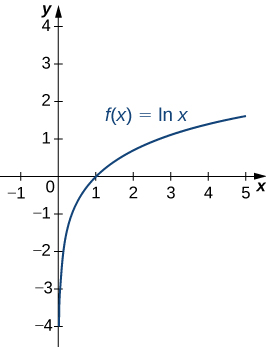
La fonction\(\ln x\) est dérivable ; elle est donc continue.
Un graphique de\(\ln x\) est illustré sur la figure. Notez qu'il est continu dans tout son domaine de\((0,∞)\).
Calculez les dérivées suivantes :
- \(\dfrac{d}{dx}\Big(\ln (5x^3−2)\Big)\)
- \(\dfrac{d}{dx}\Big((\ln (3x))^2\Big)\)
Solution
Nous devons appliquer la règle de la chaîne dans les deux cas.
- \(\dfrac{d}{dx}\Big(\ln (5x^3−2)\Big)=\dfrac{15x^2}{5x^3−2}\)
- \(\dfrac{d}{dx}\Big((\ln (3x))^2\Big)=\dfrac{2(\ln (3x))⋅3}{3x}=\dfrac{2(\ln (3x))}{x}\)
Calculez les dérivées suivantes :
- \(\dfrac{d}{dx}\Big(\ln (2x^2+x)\Big)\)
- \(\dfrac{d}{dx}\Big((\ln (x^3))^2\Big)\)
- Allusion
-
Appliquez la formule de différenciation qui vient d'être fournie et utilisez la règle de chaîne si nécessaire.
- Réponse
-
un.\(\dfrac{d}{dx}\Big(\ln (2x^2+x)\Big)=\dfrac{4x+1}{2x^2+x}\)
b.\(\dfrac{d}{dx}\Big((\ln (x^3))^2\Big)=\dfrac{6\ln (x^3)}{x}\)
Notez que si nous utilisons la fonction de valeur absolue et que nous créons une nouvelle fonction\(\ln |x|\), nous pouvons étendre le domaine du logarithme naturel pour l'inclure\(x<0\). Alors\(\dfrac{d}{dx}\Big( \ln x \Big)=\dfrac{1}{x}\). Cela donne naissance à la formule d'intégration familière.
Le logarithme naturel est l'antidérivée de la fonction\(f(u)=\dfrac{1}{u}\) :
\[∫\dfrac{1}{u}\,du=\ln |u|+C. \nonumber \]
Calculer l'intégrale\(\displaystyle ∫\dfrac{x}{x^2+4}\,dx.\)
Solution
En utilisant\(u\) -substitution, laissez\(u=x^2+4\). Ensuite,\(du=2x\,dx\) et nous avons
\(\displaystyle ∫\dfrac{x}{x^2+4}\,dx=\dfrac{1}{2}∫\dfrac{1}{u}\,du=\dfrac{1}{2}\ln |u|+C=\dfrac{1}{2}\ln |x^2+4|+C=\dfrac{1}{2}\ln (x^2+4)+C.\)
Calculer l'intégrale\(\displaystyle ∫\dfrac{x^2}{x^3+6}\,dx.\)
- Allusion
-
Appliquez la formule d'intégration fournie précédemment et utilisez la substitution u si nécessaire.
- Réponse
-
\(\displaystyle ∫\dfrac{x^2}{x^3+6}\,dx=\dfrac{1}{3}\ln ∣x^3+6∣+C\)
Bien que nous ayons appelé notre fonction « logarithme », nous n'avons pas réellement prouvé qu'aucune des propriétés des logarithmes est valable pour cette fonction. C'est ce que nous faisons ici.
Si\(a,\, b>0\) et\(r\) est un nombre rationnel, alors
- \(\ln 1=0\)
- \(\ln (ab)=\ln a+\ln b\)
- \(\ln \left(\dfrac{a}{b}\right)=\ln a−\ln b\)
- \(\ln \left(a^r\right)=r\ln a\)
i. Par définition,\(\displaystyle \ln 1=∫^1_1\dfrac{1}{t}\,dt=0.\)
ii. Nous avons
\(\displaystyle \ln (ab)=∫^{ab}_1\dfrac{1}{t}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_a\dfrac{1}{t}\,dt.\)
\(u-substitution\)À utiliser sur la dernière intégrale de cette expression. Laissez\(u=t/a\). Ensuite\(du=(1/a)dt.\), en plus\(t=a,\, u=1\), quand et quand\(t=ab,\, u=b.\) Nous obtenons
\(\displaystyle \ln (ab)=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_a\dfrac{1}{t}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^{ab}_1\dfrac{a}{t}⋅\dfrac{1}{a}\,dt=∫^a_1\dfrac{1}{t}\,dt+∫^b_1\dfrac{1}{u}\,du=\ln a+\ln b.\)
iii. Notez que
\(\dfrac{d}{dx}\Big(\ln (x^r)\Big)=\dfrac{rx^{r−1}}{x^r}=\dfrac{r}{x}\).
En outre,
\(\dfrac{d}{dx}\Big((r\ln x)\Big)=\dfrac{r}{x}.\)
Puisque les dérivées de ces deux fonctions sont les mêmes, selon le théorème fondamental du calcul, elles doivent différer d'une constante. Nous avons donc
\(\ln (x^r)=r\ln x+C\)
pour une certaine constante\(C\). En prenant\(x=1\), on obtient
\(\ln (1^r)=r\ln (1)+C\)
\(0=r(0)+C\)
\(C=0.\)
Ainsi\(\ln (x^r)=r\ln x\), la preuve est complète. Notez que nous pouvons étendre cette propriété aux valeurs irrationnelles présentées\(r\) plus loin dans cette section.
La partie iii. fait suite aux parties ii. et iv. et la preuve vous est laissée.
□
Utilisez les propriétés des logarithmes pour simplifier l'expression suivante en un seul logarithme :
\( \ln 9−2 \ln 3+\ln \left(\tfrac{1}{3}\right).\)
Solution
Nous avons
\( \ln 9−2 \ln 3+\ln \left(\tfrac{1}{3}\right)=\ln (3^2)−2 \ln 3+\ln (3^{−1})=2\ln 3−2\ln 3−\ln 3=−\ln 3.\)
Utilisez les propriétés des logarithmes pour simplifier l'expression suivante en un seul logarithme :
\( \ln 8−\ln 2−\ln \left(\tfrac{1}{4}\right)\)
- Allusion
-
Appliquez les propriétés des logarithmes.
- Réponse
-
\(4\ln 2\)
Définition du nombre e
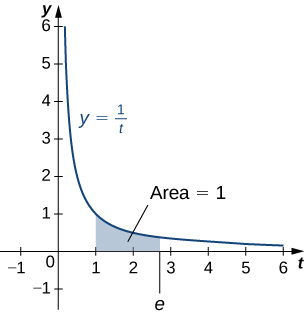
Maintenant que le logarithme naturel est défini, nous pouvons utiliser cette fonction pour définir le nombre\(e\).
Le nombre\(e\) est défini comme étant le nombre réel, de telle sorte que
\[\ln e=1\nonumber \]
En d'autres termes, l'aire sous la courbe\(y=1/t\) entre\(t=1\) et\(t=e\) est\(1\) (Figure). La preuve qu'un tel numéro existe et qu'il est unique vous est laissée. (Conseil : utilisez le théorème des valeurs intermédiaires pour prouver l'existence et le fait qu'elle\(\ln x\) augmente pour prouver l'unicité.)
Ce chiffre\(e\) peut s'avérer irrationnel, mais nous ne le ferons pas ici (voir la série Student Project in Taylor and Maclaurin). Sa valeur approximative est donnée par
\( e≈2.71828182846.\)
La fonction exponentielle
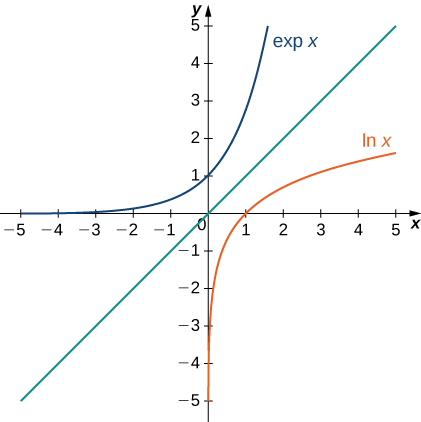
Nous allons maintenant porter notre attention sur la fonction\(e^x\). Notez que le logarithme naturel est un pour un et possède donc une fonction inverse. Pour l'instant, nous désignons cette fonction inverse par\(\exp x\). Ensuite,
\[ \exp(\ln x)=x \nonumber \]
pour\(x>0\) et
\[ \ln (\exp x)=x \nonumber \]
pour tous\(x\).
La figure suivante montre les graphiques de\(\exp x\) et\(\ln x\).
Nous émettons cette hypothèse\(\exp x=e^x\). Pour des valeurs rationnelles de\(x\), cela est facile à montrer. C'\(x\)est rationnel, alors nous l'avons fait\(\ln (e^x)=x\ln e=x\). Donc, quand\(x\) c'est rationnel,\(e^x=\exp x\). Pour les valeurs irrationnelles de\(x\), nous les définissons simplement\(e^x\) comme la fonction inverse de\(\ln x\).
Pour tout nombre réel\(x\), définissez\(y=e^x\) comme étant le nombre pour lequel
\[\ln y=\ln (e^x)=x. \nonumber \]
Alors nous avons\(e^x=\exp x\) pour tous\(x\), et donc
\(e^{\ln x}=x\)pour\(x>0\) et\(\ln (e^x)=x\)
pour tous\(x\).
Propriétés de la fonction exponentielle
Puisque la fonction exponentielle a été définie en termes de fonction inverse, et non en termes de puissance de,\(e\) nous devons vérifier que les lois habituelles des exposants s'appliquent à la fonction\(e^x\).
Si\(p\) et\(q\) sont des nombres réels et\(r\) est un nombre rationnel, alors
- \(e^pe^q=e^{p+q}\)
- \(\dfrac{e^p}{e^q}=e^{p−q}\)
- \((e^p)^r=e^{pr}\)
Notez que si\(p\) et\(q\) sont rationnels, les propriétés sont valables. Toutefois, si\(p\) ou si elles\(q\) sont irrationnelles, nous devons appliquer la définition de la fonction inverse de\(e^x\) et vérifier les propriétés. Seule la première propriété est vérifiée ici ; les deux autres vous sont laissées. Nous avons
\[ \ln (e^pe^q)=\ln (e^p)+\ln (eq)=p+q=\ln (e^{p+q}).\nonumber \]
Puisque\(\ln x\) c'est un à un, alors
\[ e^pe^q=e^{p+q}.\nonumber \]
□
Comme pour la partie iv. des propriétés du logarithme, nous pouvons étendre la propriété iii. à des valeurs irrationnelles de\(r\), et nous le faisons à la fin de la section.
Nous voulons également vérifier la formule de différenciation de la fonction\(y=e^x\). Pour ce faire, nous devons utiliser une différenciation implicite. Laissez\(y=e^x\). Alors
\[ \begin{align*} \ln y &=x \\[5pt] \dfrac{d}{dx}\Big(\ln y\Big) &=\dfrac{d}{dx}\Big(x\Big) \\[5pt] \dfrac{1}{y}\dfrac{dy}{dx} &=1 \\[5pt] \dfrac{dy}{dx} &=y. \end{align*}\]
Ainsi, nous voyons
\[ \dfrac{d}{dx}\Big(e^x\Big)=e^x \nonumber \]
comme vous le souhaitez, ce qui conduit immédiatement à la formule d'intégration
\[ ∫e^x \,dx=e^x+C. \nonumber \]
Nous appliquons ces formules dans les exemples suivants.
Évaluez les dérivés suivants :
- \(\dfrac{d}{dt}\Big(e^{3t}e^{t^2}\Big)\)
- \(\dfrac{d}{dx}\Big(e^{3x^2}\Big)\)
Solution
Nous appliquons la règle de la chaîne si nécessaire.
- \(\dfrac{d}{dt}\Big(e^{3t}e^{t^2}\Big)=\dfrac{d}{dt}\Big(e^{3t+t^2}\Big)=e^{3t+t^2}(3+2t)\)
- \(\dfrac{d}{dx}\Big(e^{3x^2}\Big)=e^{3x^2}6x\)
Évaluez les dérivés suivants :
- \(\dfrac{d}{dx}\Big(\dfrac{e^{x^2}}{e^{5x}}\Big)\)
- \(\dfrac{d}{dt}\Big((e^{2t})^3\Big)\)
- Allusion
-
Utilisez les propriétés des fonctions exponentielles et la règle de chaîne si nécessaire.
- Réponse
-
un.\(\dfrac{d}{dx}\Big(\dfrac{e^{x^2}}{e^{5x}}\Big)=e^{x^{2−5x}}(2x−5)\)
b.\(\dfrac{d}{dt}\Big((e^{2t})^3\Big)=6e^{6t}\)
Évaluez l'intégrale suivante :\(\displaystyle ∫2xe^{−x^2}\,dx.\)
Solution
En utilisant\(u\) -substitution, laissez\(u=−x^2\). Ensuite,\(du=−2x\,dx,\) et nous avons
\(\displaystyle ∫2xe^{−x^2}\,dx=−∫e^u\,du=−e^u+C=−e^{−x^2}+C.\)
Évaluez l'intégrale suivante :\(\displaystyle ∫\dfrac{4}{e^{3x}}\,dx.\)
- Allusion
-
Utilisez les propriétés des fonctions exponentielles et\(u-substitution\) selon les besoins.
- Réponse
-
\(\displaystyle ∫\dfrac{4}{e^{3x}}\,dx=−\dfrac{4}{3}e^{−3x}+C\)
Fonctions logarithmiques et exponentielles générales
Nous terminons cette section en examinant les fonctions exponentielles et les logarithmes avec des bases autres que\(e\). Les fonctions exponentielles sont des fonctions de la forme\(f(x)=a^x\). Notez qu'à moins\(a=e\) que nous n'ayons toujours pas de définition mathématiquement rigoureuse de ces fonctions pour les exposants irrationnels. Corrigons cela ici en définissant la fonction\(f(x)=a^x\) en termes de fonction exponentielle\(e^x\). Nous examinons ensuite les logarithmes avec des bases autres que e en tant que fonctions inverses de fonctions exponentielles.
Pour n'importe quel nombre réel\(a>0,\) et pour n'importe quel nombre\(x\), définissez\(y=a^x\) comme suit :
\[y=a^x=e^{x \ln a}. \nonumber \]
Maintenant\(a^x\) est défini rigoureusement pour toutes les valeurs de\(x\). Cette définition nous permet également de généraliser la propriété iv. des logarithmes et la propriété iii. des fonctions exponentielles à appliquer aux valeurs rationnelles et irrationnelles de\(r\). Il est simple de montrer que les propriétés des exposants sont valables pour les fonctions exponentielles générales définies de cette manière.
Appliquons maintenant cette définition pour calculer une formule de différenciation pour\(a^x\). Nous avons
\(\dfrac{d}{dx}\Big(a^x\Big)=\dfrac{d}{dx}\Big(e^{x\ln a}\Big)=e^{x\ln a}\ln a=a^x\ln a.\)
La formule d'intégration correspondante suit immédiatement.
Laissez\(a>0.\) alors,
\[\dfrac{d}{dx}\Big(a^x\Big)=a^x \ln a \nonumber \]
et
\[∫a^x\,dx=\dfrac{1}{\ln a}a^x+C. \nonumber \]
Si\(a≠1\), alors la fonction\(a^x\) est biunivoque et possède un inverse bien défini. Son inverse est indiqué par\(\log_a x\). Ensuite,
\( y=\log_a x\)si et seulement si\(x=a^y.\)
Notez que les fonctions logarithmiques générales peuvent être écrites en termes de logarithme naturel. Laissez\(y=\log_a x.\) alors,\(x=a^y\). En prenant le logarithme naturel des deux côtés de cette deuxième équation, nous obtenons
\ [\ begin {align*} \ ln x &= \ ln (a^y) \ \ [5 points]
\ ln x&=y \ ln a \ \ [5 points]
y&= \ dfrac {\ ln x} {\ ln a} \ \ [5 points]
\ log_a x&= \ dfrac {\ ln x} {\ ln a}. \ end {align*} \]
Ainsi, nous voyons que toutes les fonctions logarithmiques sont des multiples constants les unes des autres. Ensuite, nous utilisons cette formule pour trouver une formule de différenciation pour un logarithme avec base\(a\). Encore une fois, laissez\(y=\log_a x\). Ensuite,
\ [\ begin {align*} \ dfrac {dy} {dx} &= \ dfrac {d} {dx} \ Big (\ log_a x \ Big) \ \ [5pt]
&= \ dfrac {d} {dx} \ left (\ dfrac {\ ln x} {\ ln a} \ right) \ \ [5 points] & =( \ dfrac {\ ln x} {\ ln a} \ right) \ \ [5 points]
& =( \ dfrac {\ ln x} {\ ln a} \ right) \ \ [5 points] & {1} {\ ln a}) \ dfrac {d} {dx} \ Big (\ ln x \ Big) \ \ [5 points]
&= \ dfrac {1} {\ ln a} ⋅ \ dfrac {1} {x} = \ dfrac {1} {x \ ln a} \ end {align*} \]
Laissez\(a>0.\) alors,
\[\dfrac{d}{dx}\Big(\log_a x\Big)=\dfrac{1}{x\ln a}. \nonumber \]
Évaluez les dérivés suivants :
- \(\dfrac{d}{dt}\Big(4^t⋅2^{t^2}\Big)\)
- \(\dfrac{d}{dx}\Big(\log_8(7x^2+4)\Big)\)
Solution : Nous devons appliquer la règle de la chaîne si nécessaire.
- \(\dfrac{d}{dt}\Big(4^t⋅2^{t^2}\Big)=\dfrac{d}{dt}\Big(2^{2t}⋅2^{t^2}\Big)=\dfrac{d}{dt}\Big(2^{2t+t^2}\Big)=2^{2t+t^2}\ln (2)(2+2t)\)
- \(\dfrac{d}{dx}\Big(\log_8(7x^2+4)\Big)=\dfrac{1}{(7x^2+4)(\ln 8)}(14x)\)
Évaluez les dérivés suivants :
- \(\dfrac{d}{dt}\Big(4^{t^4}\Big)\)
- \(\dfrac{d}{dx}\Big(\log_3(\sqrt{x^2+1})\Big)\)
- Allusion
-
Utilisez les formules et appliquez la règle de chaîne si nécessaire.
- Réponse
-
un.\(\dfrac{d}{dt}\Big(4^{t^4}\Big)=4^{t^4}(\ln 4)(4t^3)\)
b.\(\dfrac{d}{dx}\Big(\log_3(\sqrt{x^2+1})\Big)=\dfrac{x}{(\ln 3)(x^2+1)}\)
Évaluez l'intégrale suivante :\(\displaystyle ∫\dfrac{3}{2^{3x}}\,dx.\)
Solution
Utilisez\(u-substitution\) et laissez\(u=−3x\). Ensuite,\(du=−3\,dx\) et nous avons
\[ ∫\dfrac{3}{2^{3x}}\,dx=∫3⋅2^{−3x}\,dx=−∫2^u\,du=−\dfrac{1}{\ln 2}2^u+C=−\dfrac{1}{\ln 2}2^{−3x}+C.\nonumber \]
Évaluez l'intégrale suivante :\(\displaystyle ∫x^2 2^{x^3}\,dx.\)
- Allusion
-
Utiliser les propriétés des fonctions exponentielles et de la substitution u
- Réponse
-
\(\displaystyle ∫x^2 2^{x^3}\,dx=\dfrac{1}{3\ln 2}2^{x^3}+C\)
Concepts clés
- Le traitement antérieur des logarithmes et des fonctions exponentielles ne définissait pas les fonctions de manière précise et formelle. Cette section développe les concepts d'une manière mathématiquement rigoureuse.
- La pierre angulaire du développement est la définition du logarithme naturel en termes d'intégrale.
- La fonction\(e^x\) est ensuite définie comme l'inverse du logarithme naturel. Les fonctions exponentielles générales sont définies en termes de\(e^x\), et les fonctions inverses correspondantes sont des logarithmes généraux.
- Les propriétés familières des logarithmes et des exposants sont toujours valables dans ce contexte plus rigoureux.
Équations clés
- Fonction logarithmique naturelle
- \(\displaystyle \ln x=∫^x_1\dfrac{1}{t}\,dt\)
- Fonction exponentielle\(y=e^x\)
- \(\ln y=\ln (e^x)=x\)


