Skip to main content
Global

6.6E : Exercices pour la section 6.6

  1. Last updated
  2. Save as PDF
  • Page ID
    197275

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Dans les exercices 1 à 6, calculez le centre de gravité pour la collection des masses données.

    1)\(m_1=2\) à\(x_1=1\) et\(m_2=4\) à\(x_2=2\)

    2)\(m_1=1\) à\(x_1=−1\) et\(m_2=3\) à\(x_2=2\)

    Réponse
    \(x = \frac{5}{4}\)

    3)\(m=3\) à\(x=0,1,2,6\)

    4) Masses unitaires à\((x,y)=(1,0),(0,1),(1,1)\)

    Réponse
    \(\left(\frac{2}{3},\, \frac{2}{3}\right)\)

    5)\(m_1=1\) à\((1,0)\) et\(m_2=4\) à\((0,1)\)

    6)\(m_1=1\) à\((1,0)\) et\(m_2=3\) à\((2,2)\)

    Réponse
    \(\left(\frac{7}{4},\,\frac{3}{2}\right)\)

    Dans les exercices 7 à 16, calculez le centre de gravité\(\bar x.\)

    7)\(ρ=1\) pour\(x∈(−1,3)\)

    8)\(ρ=x^2\) pour\(x∈(0,L)\)

    Réponse
    \(\dfrac{3L}{4}\)

    9)\(ρ=1\) pour\(x∈(0,1)\) et\(ρ=2\) pour\(x∈(1,2)\)

    10)\(ρ=\sin x\) pour\(x∈(0,π)\)

    Réponse
    \(\frac{π}{2}\)

    11)\(ρ=\cos x\) pour\(x∈\left(0,\frac{π}{2}\right)\)

    12)\(ρ=e^x\) pour\(x∈(0,2)\)

    Réponse
    \(\dfrac{e^2+1}{e^2−1}\)

    13)\(ρ=x^3+xe^{−x}\) pour\(x∈(0,1)\)

    14)\(ρ=x\sin x\) pour\(x∈(0,π)\)

    Réponse
    \(\dfrac{π^2−4}{π}\)

    15)\(ρ=\sqrt{x}\) pour\(x∈(1,4)\)

    16)\(ρ=\ln x\) pour\(x∈(1,e)\)

    Réponse
    \(\frac{1}{4}(1+e^2)\)

    Dans les exercices 17 à 19, calculez le centre de gravité\((\bar{x},\bar{y}).\) Utilisez la symétrie pour localiser le centre de gravité chaque fois que possible.

    17)\(ρ=7\) sur la place\(0≤x≤1, \; 0≤y≤1\)

    18)\(ρ=3\) dans le triangle avec des sommets\((0,0), \, (a,0)\), et\((0,b)\)

    Réponse
    \(\left(\frac{a}{3},\, \frac{b}{3}\right)\)

    19)\(ρ=2\) pour la région délimitée par\(y=\cos(x), \; y=−\cos(x), \; x=−\frac{π}{2}\), et\(x=\frac{π}{2}\)

    Dans les exercices 20 à 26, utilisez une calculatrice pour dessiner la région, puis calculez le centre de gravité\((\bar{x},\bar{y}).\) Utilisez la symétrie pour localiser le centre de gravité chaque fois que possible.

    20) [T] La région délimitée par\(y=\cos(2x), \; x=−\frac{π}{4}\), et\(x=\frac{π}{4}\)

    Réponse
    \(\left(0,\frac{π}{8}\right)\)

    21) [T] La région entre\(y=2x^2, \; y=0, \; x=0,\) et\(x=1\)

    22) [T] La région entre\(y=\frac{5}{4}x^2\) et\(y=5\)

    Réponse
    \((0,3)\)

    23) [T] Région comprise entre\(y=\sqrt{x}, \; y=\ln x, \; x=1,\) et\(x=4\)

    24) [T] La région délimitée par\(y=0\) et\(\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)

    Réponse
    \(\left(0,\frac{4}{π}\right)\)

    25) [T] La région délimitée par\(y=0, \; x=0,\) et\(\dfrac{x^2}{4}+\dfrac{y^2}{9}=1\)

    26) [T] La région délimitée par\(y=x^2\) et\(y=x^4\) dans le premier quadrant

    Réponse
    \(\left(\frac{5}{8},\, \frac{1}{3}\right)\)

    Dans les exercices 27 à 31, utilisez le théorème de Pappus pour déterminer le volume de la forme.

    27) Rotation\(y=mx\) autour de l'\(x\)axe -entre\(x=0\) et\(x=1\)

    28) Rotation\(y=mx\) autour de l'\(y\)axe -entre\(x=0\) et\(x=1\)

    Réponse
    \(V = \frac{mπ}{3}\)unités³

    29) Cône général créé en faisant pivoter un triangle avec des sommets\((0,0), \, (a,0),\) et\((0,b)\) autour de l'\(y\)axe. Votre réponse correspond-elle au volume d'un cône ?

    30) Un cylindre général créé en faisant pivoter un rectangle avec des sommets\((0,0), \, (a,0), \, (0,b),\) et\((a,b)\) autour de l'\(y\)axe. Votre réponse correspond-elle au volume d'une bouteille ?

    Réponse
    \(V = πa^2b\)unités³

    31) Une sphère créée en faisant tourner un demi-cercle avec un rayon\(a\) autour de l'\(y\)axe. Votre réponse correspond-elle au volume d'une sphère ?

    Dans les exercices 32 à 36, utilisez une calculatrice pour dessiner la région délimitée par la courbe. Trouvez la zone\(M\) et le centroïde\((\bar{x},\bar{y})\) pour les formes données. Utilisez la symétrie pour localiser le centre de gravité dans la mesure du possible.

    32) [T] Quart de cercle :\(y=\sqrt{1−x^2}, \; y=0\), et\(x=0\)

    Réponse
    \(\left(\frac{4}{3π},\, \frac{4}{3π}\right)\)

    33) [T] Triangle :\(y=x, \; y=2−x\), et\(y=0\)

    34) [T] Lentille :\(y=x^2\) et\(y=x\)

    Réponse
    \(\left(\frac{1}{2},\, \frac{2}{5}\right)\)

    35) [T] Bague :\(y^2+x^2=1\) et\(y^2+x^2=4\)

    36) [T] Demi-anneau :\(y^2+x^2=1, \; y^2+x^2=4,\) et\(y=0\)

    Réponse
    \(\left(0,\, \frac{28}{9π}\right)\)

    37) Déterminez le centre de gravité généralisé dans le ruban entre\(y=x^a\) et\(y=x^b\) avec\(a>b\). Ensuite, utilisez le théorème de Pappus pour déterminer le volume du solide généré lors de la rotation autour de l'\(y\)axe.

    38) Trouvez le centre de gravité généralisé entre\(y=a^2−x^2, \; x=0\), et\(y=0\). Ensuite, utilisez le théorème de Pappus pour déterminer le volume du solide généré lors de la rotation autour de l'\(y\)axe.

    Réponse
    Centre de gravité :\(\left(\frac{a}{6},\,\frac{4a^2}{5}\right),\)
    Volume :\(\dfrac{2πa^4}{9}\) unités³

    39) Trouvez le centre de masse généralisé entre\(y=b\sin(ax),\; x=0,\) et\(x=\dfrac{π}{a}.\) Ensuite, utilisez le théorème de Pappus pour trouver le volume du solide généré lors de la rotation autour de l'\(y\)axe.

    40) Utilisez le théorème de Pappus pour déterminer le volume d'un tore (illustré ici). Supposons qu'un disque de rayon\(a\) soit positionné avec l'extrémité gauche du cercle\(x=b, \, b>0,\) et qu'il pivote autour de\(y\) cet axe.

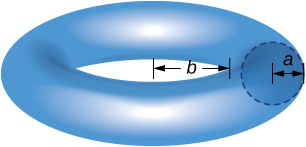
    Cette figure est un tore. Son rayon intérieur est b. À l'intérieur du tore se trouve une section transversale circulaire. Le cercle a un rayon a.

    Réponse
    Volume :\(V = 2\pi^2a^2(b+a)\)

    41) Trouvez le centre de gravité\((\bar{x},\bar{y})\) d'un fil fin le long du demi-cercle\(y=\sqrt{1−x^2}\) avec une unité de masse. (Astuce : utilisez le théorème de Pappus.)