6.6 : Moments et centres de la messe

Last updated
Save as PDF

Page ID: 197263

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objectifs d'apprentissage

Détermine le centre de gravité des objets répartis le long d'une ligne.
Localisez le centre de gravité d'une plaque mince.
Utilisez la symétrie pour localiser le centroïde d'une plaque mince.
Appliquez le théorème de Pappus pour le volume.

Dans cette section, nous examinons les centres de masse (également appelés centroïdes, sous certaines conditions) et les moments. L'idée de base du centre de gravité est la notion de point d'équilibre. Beaucoup d'entre nous ont vu des artistes faire tourner des planches au bout de bâtons. Les interprètes essaient de faire tourner plusieurs d'entre eux sans laisser tomber aucun d'entre eux. Si l'on regarde une seule assiette (sans la faire tourner), il y a un point idéal sur l'assiette où elle s'équilibre parfaitement sur le bâton. Si nous plaçons le bâton ailleurs que dans ce point idéal, l'assiette ne s'équilibre pas et elle tombe au sol. (C'est pourquoi les artistes font tourner les plaques ; la rotation aide à empêcher les plaques de tomber même si le bâton n'est pas exactement au bon endroit.) Mathématiquement, ce point idéal est appelé le centre de gravité de la plaque.

Dans cette section, nous examinons d'abord ces concepts dans un contexte unidimensionnel, puis nous étendons notre développement aux centres de masse des régions bidimensionnelles et à la symétrie. Enfin, nous utilisons les centroïdes pour déterminer le volume de certains solides en appliquant le théorème de Pappus.

Centre de la messe et des moments

Commençons par examiner le centre de gravité dans un contexte unidimensionnel. Considérez un fil ou une tige long et mince de masse négligeable reposant sur un point d'appui, comme le montre la figure\(\PageIndex{1a}\). Supposons maintenant que nous placions des objets ayant des masses\(m_1\)\(d_1\) et\(m_2\) à des distances et à\(d_2\) partir du point d'appui, respectivement, comme indiqué sur la figure\(\PageIndex{1b}\).

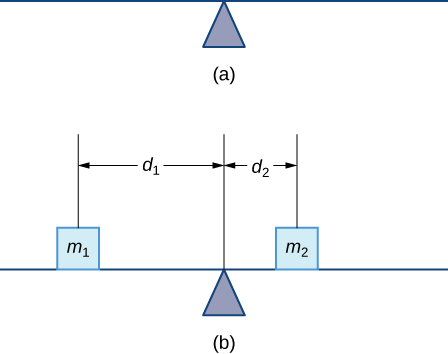
Cette figure comporte deux images. La première image est une ligne horizontale au-dessus d'un triangle équilatéral. Elle représente une tige posée sur un point d'appui. La deuxième image est identique à la première avec deux carrés sur la ligne. Ils sont étiquetés msub1 et msub2. La distance entre msub1 et le point d'appui est dsub1. La distance entre msub2 et le point d'appui est dsub2. — Figure\(\PageIndex{1}\) : (a) Une fine tige repose sur un point d'appui. (b) Les masses sont placées sur la tige.

L'exemple le plus courant d'un tel système dans la vie réelle est celui d'un terrain de jeu à bascule, ou balancier, où des enfants de poids différents sont assis à différentes distances du centre. Sur une balançoire, si un enfant est assis à chaque extrémité, l'enfant le plus lourd s'enfonce et l'enfant le plus léger est soulevé en l'air. Mais si l'enfant le plus lourd glisse vers le centre, la balançoire s'équilibre. En appliquant ce concept aux masses sur la tige, nous remarquons que les masses s'équilibrent si et seulement si

\[m_1d_1=m_2d_2. \nonumber \]

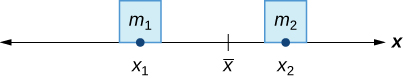
Cette figure est une image de l'axe X. Sur l'axe se trouve un point intitulé « x bar ». Sur l'axe se trouve également un point xsub1 surmonté d'un carré. À l'intérieur du carré se trouve l'étiquette msub1. Il existe également un point xsub2 sur l'axe. Au-dessus de ce point se trouve un carré. À l'intérieur du carré se trouve l'étiquette msub2. — Figure\(\PageIndex{2}\) : Le centre de gravité\(\bar{x}\) est le point d'équilibre du système.

Dans l'exemple de la bascule, nous avons équilibré le système en déplaçant les masses (les enfants) par rapport au point d'appui. Cependant, nous nous intéressons vraiment aux systèmes dans lesquels les masses ne sont pas autorisées à se déplacer, et nous équilibrons le système en déplaçant le point d'appui. Supposons que nous ayons deux masses de points\(m_1\) et\(m_2\) que nous soyons situés sur une ligne numérique aux points\(x_1\) et\(x_2\), respectivement (Figure\(\PageIndex{2}\)). Le centre de gravité,\(\bar{x}\), est le point où le point d'appui doit être placé pour équilibrer le système.

Ainsi, nous avons

\[ \begin{align*} m_1|x_1−\bar{x}| &=m_2|x_2−\bar{x}| \\[4pt] m_1(\bar{x}−x_1) &=m_2(x_2−\bar{x}) \\[4pt] m_1\bar{x}−m_1x_1 &=m_2x_2−m_2\bar{x} \\[4pt] \bar{x}(m_1+m_2) &=m_1x_1+m_2x_2 \end{align*} \nonumber \]

\[ \bar{x} =\dfrac{m_1x_1+m_2x_2}{m_1+m_2} \label{COM} \]

L'expression du numérateur de l'équation \ ref {COM}\(m_1x_1+m_2x_2\),, est appelée le premier moment du système par rapport à l'origine. Si le contexte est clair, nous laissons souvent tomber le mot en premier et désignons simplement cette expression comme le moment du système. L'expression du dénominateur,\(m_1+m_2\), est la masse totale du système. Ainsi, le centre de masse du système est le point auquel la masse totale du système peut être concentrée sans modifier le moment.

Cette idée ne se limite pas à deux masses de points. En général, si\(n\) les masses\(m_1,m_2,…,m_n,\) sont placées sur une ligne numérique à des points\(x_1,x_2,…,x_n,\) respectivement, alors le centre de gravité du système est donné par

\[ \bar{x}=\dfrac{\displaystyle {\sum_{i=1}^nm_ix_i}}{\displaystyle {\sum_{i=1}^nm_i}} \nonumber \]

Centre de masse des objets sur une ligne

\(m_1,m_2,…,m_n\)Soit des masses de points placées sur une droite numérique à des points\(x_1,x_2,…,x_n\), respectivement, et\(\displaystyle m=\sum_{i=1}^nm_i\) notons la masse totale du système. Ensuite, le moment du système par rapport à l'origine est donné par

\[M=\sum_{i=1}^nm_ix_i \label{moment} \]

et le centre de gravité du système est donné par

\[\bar{x}=\dfrac{M}{m}. \label{COM2a} \]

Nous appliquons ce théorème dans l'exemple suivant.

Exemple\(\PageIndex{1}\): Finding the Center of Mass of Objects along a Line

Supposons que quatre masses de points soient placées sur une ligne numérique comme suit :

\(m_1=30\,kg,\)placé à\(x_1=−2m\)
\(m_2=5\,kg,\)placé à\(x_2=3m\)
\(m_3=10\,kg,\)placé à\(x_3=6m\)
\(m_4=15\,kg,\)placé à\(x_4=−3m.\)

Solution

Trouvez le moment du système par rapport à l'origine et trouvez le centre de gravité du système.

Nous devons d'abord calculer le moment du système (équation \ ref {moment}) :

\[ \begin{align*} M &=\sum_{i=1}^4m_ix_i \\[4pt] &= −60+15+60−45 \\[4pt] &=−30. \end{align*}\]

Maintenant, pour trouver le centre de gravité, nous avons besoin de la masse totale du système :

\[ \begin{align*} m &=\sum_{i=1}^4m_i \\[4pt] &=30+5+10+15 \\[4pt] &= 60\, kg \end{align*}\]

Ensuite, nous avons (à partir de l'équation \ ref {Com2a})

\(\bar{x}–=\dfrac{M}{m}=−\dfrac{30}{60}=−\dfrac{1}{2}\).

Le centre de gravité est situé à 1/2 m à gauche de l'origine.

Exercice\(\PageIndex{1}\)

Supposons que quatre masses de points soient placées sur une ligne numérique comme suit :

\(m_1=12\,kg\)placé à\(x_1=−4m\)
\(m_2=12\,kg\)placé à\(x_2=4m\)
\(m_3=30\,kg\)placé à\(x_3=2m\)
\(m_4=6\,kg,\)placé à\(x_4=−6m.\)

Trouvez le moment du système par rapport à l'origine et trouvez le centre de gravité du système.

Allusion: Utilisez le processus de l'exemple précédent.

Réponse: \(M=24,\bar{x}=\dfrac{2}{5}m\)

Nous pouvons généraliser ce concept pour trouver le centre de masse d'un système de masses ponctuelles dans un plan. \(m_1\)Soit une masse ponctuelle située à un point\((x_1,y_1)\) du plan. Ensuite, le moment\(M_x\) de la masse par rapport à l'\(x\)axe -est donné par\(M_x=m_1y_1\). De même, le moment\(M_y\) par rapport à l'\(y\)axe -est donné par

\[M_y=m_1x_1. \nonumber \]

Notez que la\(x\) coordonnée du point est utilisée pour calculer le moment par rapport à l'\(y\)axe, et vice versa. La raison en est que la\(x\) coordonnée indique la distance entre la masse de points et l'\(y\)axe des points, et la\(y\) coordonnée indique la distance par rapport à l'\(x\)axe des points (voir la figure suivante).

Si nous avons plusieurs masses ponctuelles dans le\(xy\) plan, nous pouvons utiliser les moments par rapport aux\(y\) axes\(x\) - et - pour calculer les\(y\) coordonnées\(x\) - et - du centre de masse du système.

Centre de masse des objets dans un plan

Soit\(m_1\),\(m_2\),...,\(m_n\) des masses de points situées dans le\(xy\) plan -à des points\((x_1,y_1),(x_2,y_2),…,(x_n,y_n),\) respectivement, et\(\displaystyle m=\sum_{i=1}^nm_i\) désignons la masse totale du système. Ensuite, les moments\(M_x\) et\(M_y\) du système par rapport aux\(y\) axes\(x\) - et -, respectivement, sont donnés par

\[M_x=\sum_{i=1}^nm_iy_i \label{COM1} \]

\[M_y=\sum_{i=1}^nm_ix_i. \label{COM2} \]

De plus, les coordonnées du centre de gravité\((\bar{x},\bar{y})\) du système sont

\[\bar{x}=\dfrac{M_y}{m} \label{COM3} \]

\[\bar{y}=\dfrac{M_x}{m}. \label{COM4} \]

L'exemple suivant montre comment appliquer les formules du centre de masse (équations \ ref {COM1} - \ ref {COM4}).

Exemple\(\PageIndex{2}\): Finding the Center of Mass of Objects in a Plane

Supposons que trois masses de points soient placées dans le\(xy\) plan comme suit (supposons que les coordonnées soient données en mètres) :

\(m_1=2\,kg\)placé à\((−1,3),\)
\(m_2=6\,kg\)placé à\((1,1),\)
\(m_3=4\,kg\)placé à\((2,−2).\)

Trouvez le centre de gravité du système.

Solution

Nous calculons d'abord la masse totale du système :

\[m=\sum_{i=1}^3m_i=2+6+4=12\,kg. \nonumber \]

Nous trouvons ensuite les moments par rapport aux\(y\) axes\(x\) - et -:

\[\begin{align*} M_y &=\sum_{i=1}^3m_ix_i=−2+6+8=12, \\[4pt] M_x &=\sum_{i=1}^3m_iy_i=6+6−8=4. \end{align*}\]

Ensuite, nous avons

\[\bar{x}=\dfrac{M_y}{m}=\dfrac{12}{12}=1 \nonumber \]

\[\bar{y}=\dfrac{M_x}{m}=\dfrac{4}{12}=\dfrac{1}{3}. \nonumber \]

Le centre de gravité du système est exprimé\((1,1/3),\) en mètres.

Exercice\(\PageIndex{2}\)

Supposons que trois masses de points soient placées sur une ligne numérique comme suit (supposons que les coordonnées sont données en mètres) :

\(m_1=5\,kg,\)placé à\((−2,−3),\)
\(m_2=3\, kg,\)placé à\((2,3),\)
\(m_3=2\, kg,\)placé à\((−3,−2).\)

Trouvez le centre de gravité du système.

Allusion: Utilisez le processus de l'exemple précédent.

Réponse: \((−1,−1)\)m

Centre de masse des plaques minces

Jusqu'à présent, nous avons étudié des systèmes de masses de points sur une ligne et dans un plan. Maintenant, au lieu de concentrer la masse d'un système à des points discrets, nous voulons examiner des systèmes dans lesquels la masse du système est distribuée en continu sur une fine feuille de matériau. Pour nos besoins, nous supposons que la feuille est suffisamment fine pour pouvoir être traitée comme si elle était bidimensionnelle. Une telle feuille s'appelle une lamine. Ensuite, nous développons des techniques pour trouver le centre de masse d'une lame. Dans cette section, nous supposons également que la densité de la lame est constante.

Les lamines sont souvent représentées par une région bidimensionnelle dans un plan. Le centre géométrique d'une telle région s'appelle son centroïde. Comme nous avons supposé que la densité de la lame est constante, le centre de masse de la lame dépend uniquement de la forme de la région correspondante dans le plan ; il ne dépend pas de la densité. Dans ce cas, le centre de gravité de la lame correspond au centroïde de la région délimitée dans le plan. Comme pour les systèmes de masses ponctuelles, nous devons déterminer la masse totale de la lame, ainsi que les moments de la lame par rapport aux\(y\) axes\(x\) - et.

Nous considérons d'abord une lame en forme de rectangle. Rappelons que le centre de masse d'une lame est le point d'équilibre de la lame. Pour un rectangle, ce point est à la fois le centre horizontal et vertical du rectangle. Sur la base de cette compréhension, il est clair que le centre de gravité d'une lame rectangulaire est le point où les diagonales se croisent, ce qui est le résultat du principe de symétrie, et cela est indiqué ici sans preuve.

Le principe de symétrie

Si une région\(R\) est symétrique par rapport à une droite\(l\), le centroïde de\(R\) se trouve sur\(l\).

Passons maintenant à des lamines plus générales. Supposons que nous ayons une lame délimitée au-dessus par le graphique d'une fonction continue\(f(x)\), en dessous par l'\(x\)axe -, et à gauche et à droite par les lignes\(x=a\) et\(x=b\), respectivement, comme le montre la figure suivante.

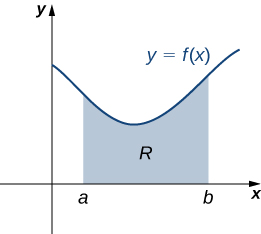
Cette image est un graphique de y=f (x). Il se trouve dans le premier quadrant. Sous la courbe se trouve une zone ombrée nommée « R ». La zone ombrée est délimitée à gauche en x=a et à droite en x=b. — Figure\(\PageIndex{4}\) : région du plan représentant une lamelle.

Comme pour les systèmes de masses ponctuelles, pour déterminer le centre de masse de la lame, nous devons déterminer la masse totale de la lame, ainsi que les moments de la lame par rapport aux\(y\) axes\(x\) - et. Comme nous l'avons fait à de nombreuses reprises auparavant, nous approximons ces quantités en divisant l'intervalle\([a,b]\) et en construisant des rectangles.

Car\(i=0,1,2,…,n,\)\(P={x_i}\) soyons une partition régulière de\([a,b]\). Rappelez-vous que nous pouvons choisir n'importe quel point de l'intervalle\([x_{i−1},x_i]\) comme notre\(x^∗_i\). Dans ce cas, nous\(x^∗_i\) voulons être la coordonnée x du centroïde de nos rectangles. Ainsi, pour\(i=1,2,…,n\), nous sélectionnons\(x^∗_i∈[x_{i−1},x_i]\) tel que\(x^∗_i\) c'est le point médian de l'intervalle. C'est-à-dire,\(x^∗_i=(x_{i−1}+x_i)/2\). Maintenant, pour\(i=1,2,…,n,\) construire un rectangle de hauteur\(f(x^∗_i)\) sur\([x_{i−1},x_i].\) Le centre de gravité de ce rectangle est\((x^∗_i,(f(x^∗_i))/2),\) comme indiqué dans la figure suivante.

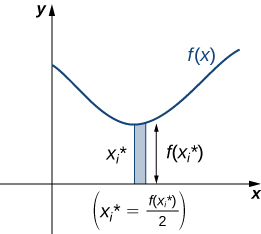
Cette figure est un graphique de la courbe étiquetée f (x). Il se trouve dans le premier quadrant. Sous la courbe et au-dessus de l'axe X se trouve un rectangle ombré vertical. La hauteur du rectangle est étiquetée f (xsubi). De plus, xsubi = f (xsubi/2). — Figure\(\PageIndex{5}\) : Un rectangle représentatif de la lame.

Ensuite, nous devons trouver la masse totale du rectangle. \(ρ\)Représentez la densité de la lame (notez qu'il\(ρ\) s'agit d'une constante). Dans ce cas,\(ρ\) est exprimé en termes de masse par unité de surface. Ainsi, pour trouver la masse totale du rectangle, on multiplie l'aire du rectangle par\(ρ\). Ensuite, la masse du rectangle est donnée par\(ρf(x^∗_i)Δx\).

Pour obtenir la masse approximative de la lame, nous ajoutons les masses de tous les rectangles pour obtenir

\[m≈\sum_{i=1}^nρf(x^∗_i)Δx. \label{eq51} \]

L'équation \ ref {eq51} est une somme de Riemann. En prenant la limite comme\(n→∞\) cela donne la masse exacte de la lame :

\[ \begin{align*} m &=\lim_{n→∞}\sum_{i=1}^nρf(x^∗_i)Δx \\[4pt] &=ρ∫^b_af(x)dx. \end{align*}\]

Ensuite, nous calculons le moment de la lame par rapport à l'axe X. Pour en revenir au rectangle représentatif, rappelez-vous que son centre de gravité est\((x^∗_i,(f(x^∗_i))/2)\). Rappelons également que le fait de traiter le rectangle comme s'il s'agissait d'une masse ponctuelle située au centre de la masse ne change pas le moment. Ainsi, le moment du rectangle par rapport à l'axe x est donné par la masse du rectangle\(ρf(x^∗_i)Δx\), multipliée par la distance entre le centre de gravité et l'axe des abscisses :\((f(x^∗_i))/2\). Par conséquent, le moment par rapport à l'axe x du rectangle est\(ρ([f(x^∗_i)]^2/2)Δx.\) en additionnant les moments des rectangles et en prenant la limite de la somme de Riemann résultante, nous voyons que le moment de la lame par rapport à l'axe x est

\[ \begin{align*}M_x &=\lim_{n→∞}\sum_{i=1}^nρ\dfrac{[f(x^∗_i)]^2}{2}Δx \\[4pt] &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx.\end{align*}\]

Nous dérivons le moment par rapport à l'axe y de la même manière, en notant que la distance entre le centre de masse du rectangle et l'axe y est de\(x^∗_i\). Ensuite, le moment de la lame par rapport à l'axe y est donné par

\[ \begin{align*}M_y &=\lim_{n→∞}\sum_{i=1}^nρx^∗_if(x^∗)i)Δx\\[4pt] &=ρ∫^b_axf(x)dx.\end{align*}\]

Nous trouvons les coordonnées du centre de masse en divisant les moments par la masse totale à donner\(\bar{x}=M_y/m\) et\(\bar{y}=M_x/m\). Si nous examinons de près les expressions pour et\(M_x,M_y\)\(m\), nous remarquons que la constante\(ρ\) annule quand\(\bar{x}\) et\(\bar{y}\) sont calculées.

Nous résumons ces résultats dans le théorème suivant.

Centre de masse d'une plaque mince dans le plan XY

Soit R une région délimitée en haut par le graphe d'une fonction continue\(f(x)\), en dessous par l'axe x, et à gauche et à droite par les lignes\(x=a\) et\(x=b\), respectivement. \(ρ\)Soit la densité de la lame associée. Ensuite, nous pouvons faire les déclarations suivantes :

La masse de la lame est\[m=ρ∫^b_af(x)dx. \label{eq4a} \]
Les moments\(M_x\) et C\(M_y\) de la lame par rapport aux axes x et y, respectivement, sont\[M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx\label{eq4b} \] et\[M_y=ρ∫^b_axf(x)dx.\label{eq4c} \]
Les coordonnées du centre de gravité\((\bar{x},\bar{y})\) sont\[\bar{x}=\dfrac{M_y}{m} \label{eq4d} \] et\[\bar{y}=\dfrac{M_x}{m}. \label{eq4e} \]

Dans l'exemple suivant, nous utilisons ce théorème pour déterminer le centre de masse d'une lame.

Exemple\(\PageIndex{3}\): Finding the Center of Mass of a Lamina

Soit R la région délimitée en haut par le graphe de la fonction\(f(x)=\sqrt{x}\) et en dessous par l'axe x sur l'intervalle\([0,4]\). Trouvez le centroïde de la région.

Solution

La région est illustrée dans la figure suivante.

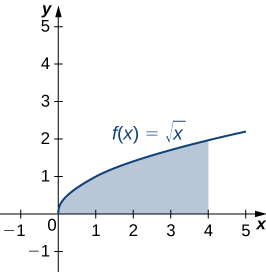
Cette figure est le graphe de la courbe f (x) = racine carrée (x). Il s'agit d'une courbe croissante dans le premier quadrant. Sous la courbe au-dessus de l'axe X se trouve une zone ombrée. Il commence à x=0 et est limité à droite à x=4. — Figure\(\PageIndex{6}\) : Déterminer le centre de gravité d'une lame.

Comme on ne nous demande que le centroïde de la région, plutôt que la masse ou les moments de la lame associée, nous savons que la constante\(ρ\) de densité finit par disparaître des calculs. Par conséquent, pour des raisons de commodité, supposons\(ρ=1\).

Nous devons d'abord calculer la masse totale (équation \ ref {eq4a}) :

\[ \begin{align*} m &=ρ∫^b_af(x)dx \\[4pt] &=∫^4_0\sqrt{x}dx \\[4pt] &=\dfrac{2}{3}x^{3/2}∣^4_0 \\[4pt] &=\dfrac{2}{3}[8−0] \\[4pt] &=\dfrac{16}{3}. \end{align*}\]

Ensuite, nous calculons les moments (équation \ ref {eq4d}) :

\[ \begin{align*} M_x &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx \\[4pt] &=∫^4_0\dfrac{x}{2}dx \\[4pt] &=\dfrac{1}{4}x^2∣^4_0 \\[4pt] &=4 \end{align*}\]

et (Équation \ ref {eq4c}) :

\[ \begin{align*} M_y &=ρ∫^b_axf(x)dx \\[4pt] &=∫^4_0x\sqrt{x}dx \\[4pt] &=∫^4_0x^{3/2}dx \\[4pt] &=\dfrac{2}{5}x^{5/2}∣^4_0 \\[4pt] &=\dfrac{2}{5}[32−0] \\[4pt] &=\dfrac{64}{5}. \end{align*}\]

Ainsi, nous avons (Équation \ ref {eq4d}) :

\[ \begin{align*} \bar{x} &=\dfrac{M_y}{m} \\[4pt] &=\dfrac{64/5}{16/3} \\[4pt] &=\dfrac{64}{5}⋅\dfrac{3}{16} \\[4pt] &=\dfrac{12}{5} \end{align*}\]

et (Équation \ ref {eq4e}) :

\[ \begin{align*} \bar{y} &=\dfrac{M_x}{y} \\[4pt] &=\dfrac{4}{16/3} \\[4pt] &=4⋅\dfrac{3}{16} \\[4pt] &=\dfrac{3}{4}. \end{align*}\]

Le centroïde de la région est\((12/5,3/4).\)

Exercice\(\PageIndex{3}\)

\(R\)Soit la région délimitée au-dessus par le graphe de la fonction\(f(x)=x^2\) et en dessous par l'axe x sur l'intervalle\([0,2].\) Trouvez le centroïde de la région.

Allusion: Utilisez le processus de l'exemple précédent.

Réponse: Le centroïde de la région est\((3/2,6/5).\)

Nous pouvons également adapter cette approche pour trouver les centroïdes de régions plus complexes. Supposons que notre région soit délimitée au-dessus par le graphe d'une fonction continue\(f(x)\), comme précédemment, mais maintenant, au lieu que la limite inférieure de la région soit l'axe x, supposons que la région soit délimitée en dessous par le graphique d'une deuxième fonction continue\(g(x)\), comme indiqué sur la figure\(\PageIndex{7}\).

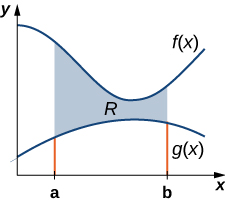
Cette figure est un graphique du premier quadrant. Il possède deux courbes. Ils sont étiquetés f (x) et g (x). f (x) est supérieur à g (x). Entre les courbes se trouve une zone ombrée appelée « R ». La zone ombrée est délimitée à gauche par x=a et à droite par x=b. — Figure\(\PageIndex{7}\) : région située entre deux fonctions.

Encore une fois, nous partitionnons l'intervalle\([a,b]\) et construisons des rectangles. Un rectangle représentatif est illustré sur la figure\(\PageIndex{8}\).

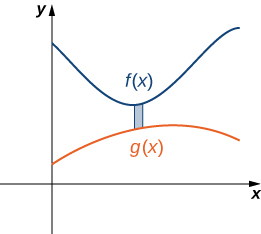
Notez que le centre de gravité de ce rectangle est\((x^∗_i,(f(x^∗_i)+g(x^∗_i))/2)\). Nous n'aborderons pas tous les détails du développement de la somme de Riemann, mais examinons certaines des étapes clés. Lors de l'élaboration des formules pour la masse de la lame et le moment par rapport à l'axe y, la hauteur de chaque rectangle est donnée par\(f(x^∗_i)−g(x^∗_i)\), ce qui conduit à l'expression\(f(x)−g(x)\) dans les intégrandes.

Lors de l'élaboration de la formule pour le moment par rapport à l'axe x, le moment de chaque rectangle est trouvé en multipliant l'aire du rectangle\(ρ[f(x^∗_i)−g(x^∗_i)]Δx,\) par la distance entre le centroïde et l'\(x\)axe\((f(x^∗_i)+g(x^∗_i))/2\) -, ce qui donne\(ρ(1/2){[f(x^∗_i)]^2−[g(x^∗_i)]^2}Δx\). En résumant ces résultats, nous arrivons au théorème suivant.

Centre de masse d'une lame délimitée par deux fonctions

\(R\)Dénotons une région délimitée en haut par le graphe d'une fonction continue, en\(f(x),\) dessous par le graphe de la fonction continue\(g(x)\), et à gauche et à droite par les lignes\(x=a\) et\(x=b\), respectivement. \(ρ\)Soit la densité de la lame associée. Ensuite, nous pouvons faire les déclarations suivantes :

La masse de la lame est\[m=ρ∫^b_a[f(x)−g(x)]dx. \nonumber \]
Les moments\(M_x\) et\(M_y\) C de la lame par rapport aux axes x et y, respectivement, sont\[M_x=ρ∫^b_a12([f(x)]^2−[g(x)]^2)dx \nonumber \] et\[M_y=ρ∫^b_ax[f(x)−g(x)]dx. \nonumber \]
Les coordonnées du centre de gravité\(\bar{x},\bar{y})\) sont\[\bar{x}=\dfrac{M_y}{m} \nonumber \] et\[\bar{y}=\dfrac{M_x}{m} \nonumber \]

Nous illustrons ce théorème dans l'exemple suivant.

Exemple\(\PageIndex{4}\): Finding the Centroid of a Region Bounded by Two Functions

Soit R la région délimitée en haut par le graphe de la fonction\(f(x)=1−x^2\) et en dessous par le graphique de la fonction\(g(x)=x−1.\) Trouvez le centroïde de la région.

Solution

La région est illustrée dans la figure suivante.

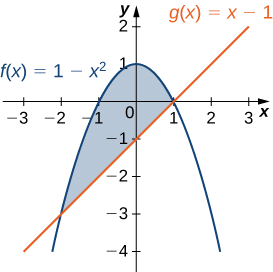
Cette figure est un graphique. Il possède deux courbes. Ils sont étiquetés f (x) =1-x^2 et g (x) =x-1. Entre les courbes se trouve une zone ombrée. La zone ombrée est délimitée à gauche par x=a et à droite par x=b. — Figure\(\PageIndex{9}\) : Déterminer le centroïde d'une région située entre deux courbes.

Les graphes des fonctions se croisent en\((−2,−3)\) et\((1,0)\), donc nous intégrons de −2 à 1. Encore une fois, pour des raisons de commodité, supposez\(ρ=1\).

Tout d'abord, nous devons calculer la masse totale :

\[ \begin{align*} m &=ρ∫^b_a[f(x)−g(x)]dx \\[4pt] &=∫^1_{−2}[1−x^2−(x−1)]dx \\[4pt] &=∫^1_{−2}(2−x^2−x)dx \\[4pt] &=\left[2x−\dfrac{1}{3}x^3−\dfrac{1}{2}x^2\right]∣^1_{−2} \\[4pt] &=\left[2−\dfrac{1}{3}−\dfrac{1}{2}\right]−\left[−4+\dfrac{8}{3}−2\right]\\[4pt] &=\dfrac{9}{2}. \end{align*}\]

Ensuite, nous calculons les moments :

\[ \begin{align*} M_x&=ρ∫^b_a\dfrac{1}{2}([f(x)]^2−[g(x)]^2)dx \\[4pt] &=\dfrac{1}{2}∫^1_{−2}((1−x^2)^2−(x−1)^2)dx\\[4pt] &=\dfrac{1}{2}∫^1_{−2}(x^4−3x^2+2x)dx \\[4pt] &=\dfrac{1}{2} \left[\dfrac{x^5}{5}−x^3+x^2\right]∣^1_{−2}\\[4pt] &=−\dfrac{27}{10} \end{align*}\]

\[ \begin{align*} M_y &=ρ∫^b_ax[f(x)−g(x)]dx \\[4pt] &=∫^1_{−2}x[(1−x^2)−(x−1)]dx\\[4pt] &=∫^1_{−2}x[2−x^2−x]dx\\[4pt] &=∫^1_{−2}(2x−x^4−x^2)dx \\[4pt] &=\left[x^2−\dfrac{x^5}{5}−\dfrac{x^3}{3}\right]∣^1_{−2}\\[4pt] &=−\dfrac{9}{4}. \end{align*}\]

Par conséquent, nous avons

\[ \begin{align*} \bar{x} &=\dfrac{M_y}{m}\\[4pt] &=−\dfrac{9}{4}⋅\dfrac{2}{9}\\[4pt] &=−\dfrac{1}{2} \end{align*}\]

\[ \begin{align*} \bar{y} &=\dfrac{M_x}{y}\\[4pt] &=−\dfrac{27}{10}⋅\dfrac{2}{9}\\[4pt] &=−\dfrac{3}{5}. \end{align*}\]

Le centroïde de la région est\((−(1/2),−(3/5)).\)

Exercice\(\PageIndex{4}\)

\(R\)Soit la région délimitée en haut par le graphe de la fonction\(f(x)=6−x^2\) et en dessous par le graphique de la fonction\(g(x)=3−2x.\) Trouvez le centroïde de la région.

Allusion: Utilisez le processus de l'exemple précédent.

Réponse: Le centroïde de la région est\((1,13/5).\)

Le principe de symétrie

Nous avons exposé le principe de symétrie plus tôt, lorsque nous examinions le centroïde d'un rectangle. Le principe de symétrie peut s'avérer très utile pour trouver les centroïdes de régions symétriques. Prenons l'exemple suivant.

Exemple\(\PageIndex{5}\): Finding the Centroid of a Symmetric Region

Soit R la région délimitée en haut par le graphe de la fonction\(f(x)=4−x^2\) et en dessous par l'axe des abscisses. Trouvez le centroïde de la région.

Solution

La région est illustrée dans la figure suivante

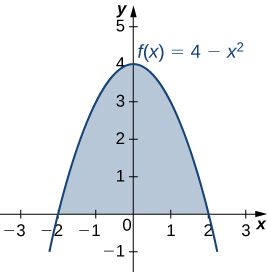
Cette figure est un graphe de la fonction f (x) =4-x^2. C'est une parabole renversée. La région située sous la parabole au-dessus de l'axe X est ombrée. La courbe coupe l'axe X en x=-2 et x=2. — Figure\(\PageIndex{10}\) : Nous pouvons utiliser le principe de symétrie pour déterminer le centroïde d'une région symétrique.

La région est symétrique par rapport à l'axe y. Par conséquent, la coordonnée x du centroïde est nulle. Il suffit de calculer\(\bar{y}\). Encore une fois, pour des raisons de commodité, supposez\(ρ=1\).

Tout d'abord, nous calculons la masse totale :

\[ \begin{align*} m &=ρ∫^b_af(x)dx \\[4pt] &=∫^2_{−2}(4−x^2)dx \\[4pt] &=\left[4x−\dfrac{x^3}{3}\right]∣^2_{−2} \\[4pt] &=\dfrac{32}{3}. \end{align*}\]

Ensuite, nous calculons les moments. Nous n'avons besoin que de\(M_x\) :

\[ \begin{align*} M_x &=ρ∫^b_a\dfrac{[f(x)]^2}{2}dx \\[4pt] &=\dfrac{1}{2}∫^2_{−2}\left[4−x^2\right]^2dx =\dfrac{1}{2}∫^2_{−2}(16−8x^2+x^4)dx \\[4pt] &=\dfrac{1}{2}\left[\dfrac{x^5}{5}−\dfrac{8x^3}{3}+16x\right]∣^2_{−2}=\dfrac{256}{15} \end{align*}\]

Ensuite, nous avons

\[\bar{y}=\dfrac{M_x}{y}=\dfrac{256}{15}⋅\dfrac{3}{32}=\dfrac{8}{5}. \nonumber \]

Le centroïde de la région est\((0,8/5).\)

Exercice\(\PageIndex{5}\)

\(R\)Soit la région délimitée en haut par le graphe de la fonction\(f(x)=1−x^2\) et en dessous par\(x\) l'axe. Trouvez le centroïde de la région.

Allusion: Utilisez le processus de l'exemple précédent.

Réponse: Le centroïde de la région est\((0,2/5).\)

Le Skywalk du Grand Canyon

Le Grand Canyon Skywalk a ouvert ses portes au public le 28 mars 2007. Cette merveille d'ingénierie est une plate-forme d'observation en forme de fer à cheval suspendue à 4000 pieds au-dessus du fleuve Colorado, sur la rive ouest du Grand Canyon. Son sol en verre cristallin offre une vue imprenable sur le canyon en contrebas (voir la figure suivante).

Cette figure est une image de la passerelle du Grand Canyon. Il s'agit d'un bâtiment situé au bord du canyon avec une passerelle qui s'étend au-dessus du canyon. — Figure\(\PageIndex{11}\) : Le Skywalk du Grand Canyon offre une vue magnifique sur le canyon. (crédit : 10da_ralta, Wikimedia Commons)

Le Skywalk est conçu en porte-à-faux, ce qui signifie que la plate-forme d'observation s'étend sur le bord du canyon, sans aucun support visible en dessous. Malgré l'absence de poteaux ou d'entretoises visibles, les structures en porte-à-faux sont conçues pour être très stables et le Skywalk ne fait pas exception. La plate-forme d'observation est solidement fixée à des poteaux de soutien qui s'étendent jusqu'à 46 pieds dans le substrat rocheux. La structure a été construite pour résister à des vents de 100 km/h et à un tremblement de terre de magnitude 8,0 dans un rayon de 50 miles, et est capable de supporter plus de 70 000 000 livres.

L'un des facteurs qui influent sur la stabilité du Skywalk est le centre de gravité de la structure. Nous allons calculer le centre de gravité du Skywalk et examiner comment le centre de gravité change lorsque les touristes entrent sur la plate-forme d'observation.

La plate-forme d'observation est en forme de U. Les jambes du U mesurent 10 pieds de large et commencent sur la terre ferme, sous le centre des visiteurs, à 48 pieds du bord du canyon. La plate-forme s'étend sur 70 pieds au-dessus du bord du canyon.

Pour calculer le centre de masse de la structure, nous la traitons comme une lame et utilisons une région bidimensionnelle dans le plan xy pour représenter la plate-forme. Nous commençons par diviser la région en trois sous-régions afin de pouvoir examiner chaque sous-région séparément. La première région, désignée\(R_1\), est constituée de la partie incurvée du U. Nous modélisons\(R_1\) comme un anneau semi-circulaire, avec un rayon intérieur de 25 pieds et un rayon extérieur de 35 pieds, centré à l'origine (Figure\(\PageIndex{12}\)).

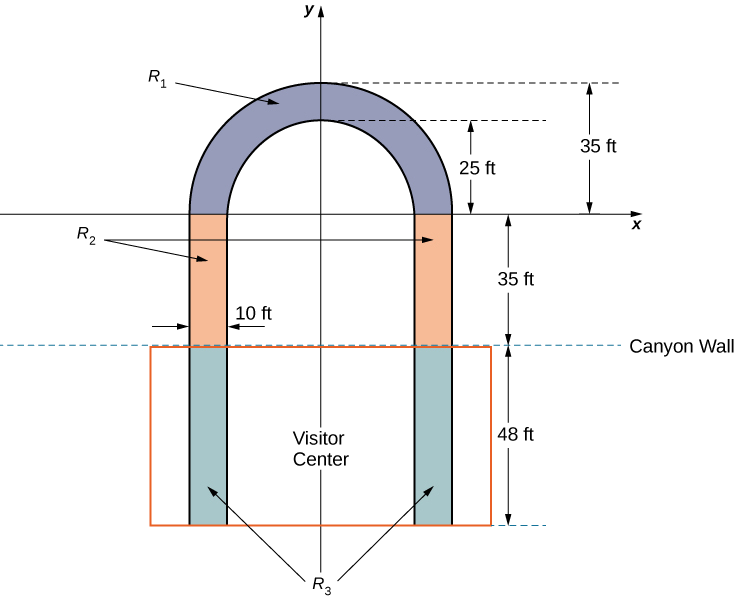
Cette figure est un croquis de la passerelle du Grand Canyon. Il se trouve sur le système de coordonnées xy. La passerelle est en forme de « U » à l'envers. Il a été divisé en trois régions. La première région en haut est intitulée « Rsub1 ». Il s'agit d'un demi-cercle avec un rayon extérieur de 35 pieds et un rayon intérieur de 25 pieds. La deuxième région est étiquetée « Rsub2 ». Il possède deux rectangles d'une largeur de 10 pieds chacun et d'une hauteur de 35 pieds. La troisième région est étiquetée « Rsub3 » et est composée de deux rectangles. Ils ont une largeur de 10 pieds et une hauteur de 48 pieds. Ils représentent la partie de la passerelle située à l'intérieur du centre d'accueil des visiteurs. — Figure\(\PageIndex{12}\) : Nous modélisons le Skywalk avec trois sous-régions.

Les pieds de la plate-forme, qui s'étendent sur 35 pieds entre la paroi du canyon\(R_1\) et la paroi du canyon, constituent la deuxième sous-région\(R_2\). Enfin, les extrémités des jambes, qui s'étendent à 48 pieds sous le centre d'accueil des visiteurs, constituent la troisième sous-région\(R_3\). Supposons que la densité de la lame soit constante et que le poids total de la plate-forme soit de 1 200 000 livres (sans compter le poids du centre d'accueil ; nous y reviendrons plus tard). Utiliser\(g=32\;ft/sec^2\).

Calculez la superficie de chacune des trois sous-régions. Notez que les zones des régions\(R_2\) et\(R_3\) doivent inclure uniquement les zones des jambes, et non l'espace libre qui les sépare. L'arrondi répond au pied carré le plus proche.
Déterminez la masse associée à chacune des trois sous-régions.
Calculez le centre de gravité de chacune des trois sous-régions.
Maintenant, traitez chacune des trois sous-régions comme une masse de points située au centre de masse de la sous-région correspondante. À l'aide de cette représentation, calculez le centre de gravité de l'ensemble de la plate-forme.
Supposons que le centre d'accueil pèse 2 200 000 livres, avec un centre de gravité correspondant au centre de masse de\(R_3\) .En traitant le centre d'accueil comme une masse ponctuelle, recalculez le centre de masse du système. Comment change le centre de gravité ?
Bien que le Skywalk ait été construit pour limiter le nombre de personnes sur la plate-forme d'observation à 120, la plate-forme peut accueillir jusqu'à 800 personnes pesant 200 livres chacune. Si les 800 personnes étaient toutes autorisées à monter sur la plate-forme et qu'elles se rendaient toutes à l'extrémité la plus éloignée de la plate-forme, comment le centre de gravité du système serait-il affecté ? (Incluez le centre d'accueil dans les calculs et représentez les personnes par une masse de points située au bord le plus éloigné de la plate-forme, à 70 pieds de la paroi du canyon.)

Théorème de Pappus

Cette section se termine par une discussion du théorème de Pappus pour le volume, qui nous permet de déterminer le volume de types particuliers de solides en utilisant le centroïde. (Il existe également un théorème de Pappus pour la surface, mais il est beaucoup moins utile que le théorème du volume.)

Théorème de Pappus pour le volume

\(R\)Soit une région du plan et soit l une ligne du plan qui ne se croise pas\(R\). Ensuite, le volume du solide de révolution formé en tournant\(R\) autour de l est égal à l'aire de\(R\) multipliée par la distance d parcourue par le centroïde de\(R\).

Une preuve

Nous pouvons prouver le cas lorsque la région est délimitée en haut par le graphe d'une fonction\(f(x)\) et en dessous par le graphique d'une fonction\(g(x)\) sur un intervalle\([a,b]\), et pour laquelle l'axe de révolution est l'\(y\)axe. Dans ce cas, la superficie de la région est\(\displaystyle A=∫^b_a[f(x)−g(x)]\,dx\). Puisque l'axe de rotation est l'\(y\)axe -, la distance parcourue par le centroïde de la région dépend uniquement de la\(x\) coordonnée -du centroïde\(\bar{x}\), qui est

\[x=\dfrac{M_y}{m}, \nonumber \]

où

\[m=ρ∫^b_a[f(x)−g(x)]dx \nonumber \]

\[M_y=ρ∫^b_ax[f(x)−g(x)]dx. \nonumber \]

Ensuite,

\[d=2π\dfrac{\displaystyle {ρ∫^b_ax[f(x)−g(x)]dx}}{\displaystyle{ρ∫^b_a[f(x)−g(x)]dx}} \nonumber \]

et donc

\[d⋅A=2π∫^b_ax[f(x)−g(x)]dx. \nonumber \]

Cependant, en utilisant la méthode des coques cylindriques, nous avons

\[V=2π∫^b_ax[f(x)−g(x)]dx. \nonumber \]

Donc,

\[V=d⋅A \nonumber \]

et la preuve est complète.

□

Exemple\(\PageIndex{6}\): Using the Theorem of Pappus for Volume

\(R\)Soit un cercle de rayon 2 centré sur\((4,0).\) Utilisez le théorème de Pappus pour le volume pour trouver le volume du tore généré en tournant\(R\) autour de l'\(y\)axe.

Solution

La région et le tore sont représentés dans la figure suivante.

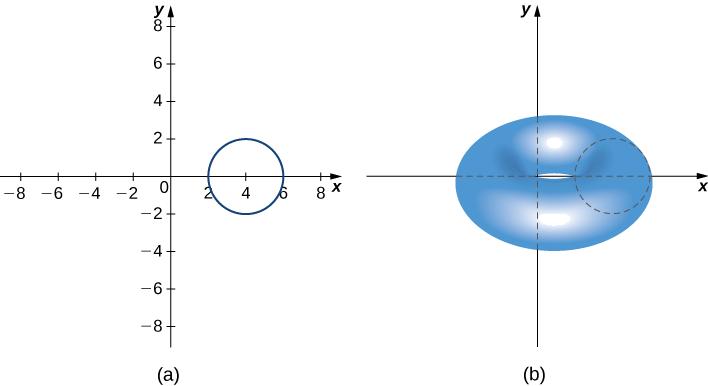
Cette figure comporte deux graphiques. Le premier est le système de coordonnées x y avec un cercle centré sur l'axe x à x=4. Le rayon est de 2. La deuxième figure est le système de coordonnées x y. Le cercle de la première image a été pivoté autour de l'axe Y pour former un tore. — Figure\(\PageIndex{13}\) : Déterminer le volume d'un tore à l'aide du théorème de Pappus. (a) Une région circulaire\(R\) dans le plan ; (b) le tore généré par une rotation\(R\) autour de l'\(y\)axe.

La région\(R\) est un cercle de rayon 2, donc l'aire de R est\(A=4π\;\text{units}^2\). Selon le principe de symétrie, le centroïde de R est le centre du cercle. Le centroïde se déplace autour de l'\(y\)axe -selon une trajectoire circulaire de rayon 4, de sorte que le centroïde parcourt\(d=8π\) des unités. Ensuite, le volume du tore est égal aux\(A⋅d=32π^2\) unités ³.

Exercice\(\PageIndex{6}\)

Soit R un cercle de rayon 1 centré sur\((3,0).\) Utilisez le théorème de Pappus pour le volume pour trouver le volume du tore généré par la rotation de R autour de l'\(y\)axe.

Allusion: Utilisez le processus de l'exemple précédent.

Réponse: \(6π^2\)unités ³

Concepts clés

Mathématiquement, le centre de masse d'un système est le point auquel la masse totale du système peut être concentrée sans modifier le moment. D'une manière générale, le centre de gravité peut être considéré comme le point d'équilibre du système.
Pour les masses de points réparties le long d'une droite numérique, le moment du système par rapport à l'origine est\(\displaystyle M=\sum^n_{i=1}m_ix_i.\) Pour les masses ponctuelles distribuées dans un plan, les moments du système par rapport aux\(y\) axes\(x\) - et -, respectivement, sont\(\displaystyle M_x=\sum^n_{i=1}m_iy_i\) et\(\displaystyle M_y=\sum^n_{i=}m_ix_i\), respectivement.
Pour une lame délimitée au-dessus par une fonction\(f(x)\), les moments du système par rapport aux\(y\) axes\(x\) - et -, respectivement, sont\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\) et\(\displaystyle M_y=ρ∫^b_axf(x)\,dx.\)
Les\(y\) coordonnées\(x\) - et - du centre de gravité peuvent être trouvées en divisant les moments autour de l'\(y\)axe -et autour de l'\(x\)axe -, respectivement, par la masse totale. Le principe de symétrie indique que si une région est symétrique par rapport à une ligne, le centroïde de la région se trouve sur la droite.
Le théorème de Pappus pour le volume indique que si une région tourne autour d'un axe externe, le volume du solide obtenu est égal à la surface de la région multipliée par la distance parcourue par le centroïde de la région.

Équations clés

Masse d'une lame

\(\displaystyle m=ρ∫^b_af(x)dx\)

Moments d'une lamina

\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\text{ and }M_y=ρ∫^b_axf(x)\,dx\)

Centre de masse d'une lame

\(\bar{x}=\dfrac{M_y}{m}\text{ and }\bar{y}=\dfrac{M_x}{m}\)

Lexique

centre de gravité: le point auquel la masse totale du système pourrait être concentrée sans modifier le moment

centroïde: le centre de gravité d'une région est le centre géométrique de la région ; les lamelles sont souvent représentées par des régions dans le plan ; si la lame a une densité constante, le centre de masse de la lame dépend uniquement de la forme de la région plane correspondante ; dans ce cas, le centre de masse de la lame correspond à le centroïde de la région représentative

lamina: une fine feuille de matériau ; les lamelles sont suffisamment fines pour que, à des fins mathématiques, elles puissent être traitées comme si elles étaient bidimensionnelles

moment: si n masses sont disposées sur une droite numérique, le moment du système par rapport à l'origine est donné par\(\displaystyle M=\sum^n_{i=1}m_ix_i\) ; si, au contraire, nous considérons une région du plan, délimitée au-dessus par une fonction\(f(x)\) sur un intervalle\([a,b]\), alors les moments de la région par rapport au\(x\) - et \(y\)-les axes sont donnés par\(\displaystyle M_x=ρ∫^b_a\dfrac{[f(x)]^2}{2}\,dx\) et\(\displaystyle M_y=ρ∫^b_axf(x)\,dx\), respectivement

principe de symétrie: le principe de symétrie indique que si une région\(R\) est symétrique par rapport à une droite\(I\), alors le centroïde de\(R\) se trouve sur\(I\)

théorème de Pappus pour le volume: ce théorème indique que le volume d'un solide de révolution formé en faisant tourner une région autour d'un axe externe est égal à l'aire de la région multipliée par la distance parcourue par le centroïde de la région