6.5 : Applications physiques de l'intégration
- Page ID
- 197190
- Déterminez la masse d'un objet unidimensionnel à l'aide de sa fonction de densité linéaire.
- Déterminez la masse d'un objet circulaire bidimensionnel à partir de sa fonction de densité radiale.
- Calculez le travail effectué par une force variable agissant le long d'une ligne.
- Calculez le travail effectué pour pomper un liquide d'une hauteur à une autre.
- Déterminez la force hydrostatique contre une plaque verticale immergée.
Dans cette section, nous examinons certaines applications physiques de l'intégration. Commençons par le calcul de la masse à partir d'une fonction de densité. Nous nous concentrons ensuite sur le travail et clôturons la section par une étude de la force hydrostatique.
Masse et densité
Nous pouvons utiliser l'intégration pour développer une formule de calcul de la masse basée sur une fonction de densité. Nous considérons d'abord une fine tige ou un fil. Orientez la tige de manière à ce qu'elle soit\(x\) alignée sur l'axe Y, avec l'extrémité gauche de la tige\(x=a\) et l'extrémité droite de la tige à\(x=b\) (Figure\(\PageIndex{1}\)). Notez que bien que nous décrivions la tige avec une certaine épaisseur sur les figures, à des fins mathématiques, nous supposons que la tige est suffisamment fine pour être traitée comme un objet unidimensionnel.
Si la tige a une densité constante\(ρ\), donnée en termes de masse par unité de longueur, alors la masse de la tige est juste le produit de la densité et de la longueur de la tige :\((b−a)ρ\). Cependant, si la densité de la tige n'est pas constante, le problème devient un peu plus difficile. Lorsque la densité de la tige varie d'un point à l'autre, nous utilisons une fonction de densité linéaire\(ρ(x)\), pour indiquer la densité de la tige en tout point,\(x\). \(ρ(x)\)Soit une fonction de densité linéaire intégrable. Maintenant, pour\(i=0,1,2,…,n\)\(P={x_i}\) que ce soit une partition régulière de l'intervalle\([a,b]\), et pour\(i=1,2,…,n\) choisir un point arbitraire\(x^∗_i∈[x_{i−1},x_i]\). La figure\(\PageIndex{2}\) montre un segment représentatif de la tige.
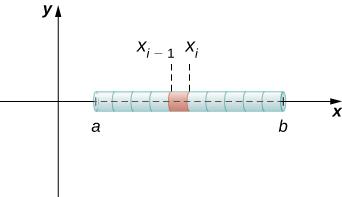
La masse\(m_i\) du segment de la tige de\(x_{i−1}\) à\(x_i\) est approximée par
\[ \begin{align*} m_i ≈ρ(x^∗_i)(x_i−x_{i−1}) \\[4pt] =ρ(x^∗_i)Δx. \end{align*} \nonumber \]
L'addition des masses de tous les segments nous donne une approximation de la masse de l'ensemble de la tige :
\[ \begin{align*} m =\sum_{i=1}^nm_i \\[4pt] ≈\sum_{i=1}^nρ(x^∗_i)Δx. \end{align*} \nonumber \]
Il s'agit d'une somme de Riemann. En prenant la limite comme suit\(n→∞\), nous obtenons une expression de la masse exacte de la tige :
\[ \begin{align*} m =\lim_{n→∞}\sum_{i=1}^nρ(x^∗_i)Δx \\[4pt] =\int ^b_aρ(x)dx. \end{align*} \nonumber \]
Nous énonçons ce résultat dans le théorème suivant.
Étant donné une tige mince orientée le long de\(x\) l'axe -sur l'intervalle\([a,b]\),\(ρ(x)\) notons une fonction de densité linéaire donnant la densité de la tige\(x\) en un point de l'intervalle. Ensuite, la masse de la tige est donnée par
\[m=\int ^b_aρ(x)dx. \label{density1} \]
Nous appliquons ce théorème dans l'exemple suivant.
Prenons l'exemple d'une fine tige orientée sur l'\(x\)axe Y sur l'intervalle\([π/2,π]\). Si la densité de la tige est donnée par\(ρ(x)=\sin x\), quelle est la masse de la tige ?
Solution
En appliquant directement l'équation \ ref {density1}, nous avons
\[ \begin{align*} m =\int ^b_aρ(x)dx \nonumber \\[4pt] = \int ^π_{π/2}\sin x \,dx \nonumber \\[4pt] = −\cos x \Big|^π_{π/2} \nonumber \\[4pt] = 1. \nonumber \end{align*}\]
Prenons l'exemple d'une fine tige orientée sur l'\(x\)axe Y sur l'intervalle\([1,3]\). Si la densité de la tige est donnée par\(ρ(x)=2x^2+3,\) quelle est la masse de la tige ?
- Allusion
-
Utilisez le processus de l'exemple précédent.
- Solution
-
\(70/3\)
Nous étendons maintenant ce concept pour trouver la masse d'un disque bidimensionnel de rayon\(r\). Comme pour la tige que nous avons examinée dans le cas unidimensionnel, nous supposons ici que le disque est suffisamment fin pour que, à des fins mathématiques, nous puissions le traiter comme un objet bidimensionnel. Nous supposons que la densité est donnée en termes de masse par unité de surface (appelée densité de surface), et supposons également que la densité ne varie que le long du rayon du disque (densité radiale). Nous orientons le disque dans le\(xy-plane\), avec le centre à l'origine. Ensuite, la densité du disque peut être traitée en fonction de\(x\), notée\(ρ(x)\). Nous supposons qu'\(ρ(x)\)il est intégrable. Comme la densité est fonction de\(x\), nous partitionnons l'intervalle\([0,r]\) le long de\(x\) l'axe. Pour\(i=0,1,2,…,n\),\(P={x_i}\) soit une partition normale de l'intervalle\([0,r]\), et pour\(i=1,2,…,n\), choisissez un point arbitraire\(x^∗_i∈[x_{i−1},x_i]\). Maintenant, utilisez la cloison pour diviser le disque en fines rondelles (bidimensionnelles). Un disque et une rondelle représentative sont représentés dans la figure suivante.
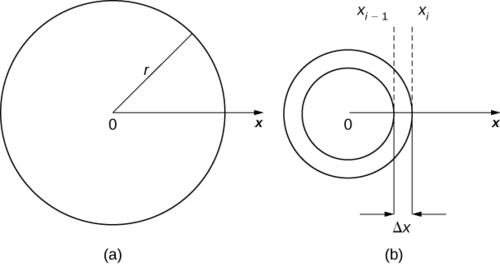
Nous approximons maintenant la densité et la surface de la laveuse pour calculer une masse approximative,\(m_i\). Notez que la surface de la laveuse est donnée par
\[ \begin{align*} A_i =π(x_i)^2−π(x_{i−1})^2 \\[4pt] =π[x^2_i−x^2_{i−1}] \\[4pt] =π(x_i+x_{i−1})(x_i−x_{i−1}) \\[4pt] =π(x_i+x_{i−1})Δx. \end{align*}\]
Vous vous souvenez peut-être que nous avions une expression similaire à celle-ci lorsque nous calculions des volumes par interpréteurs de commandes. Comme nous l'avons fait là-bas, nous utilisons\(x^∗_i≈(x_i+x_{i−1})/2\) pour approximer le rayon moyen de la laveuse. Nous obtenons
\[A_i=π(x_i+x_{i−1})Δx≈2πx^∗_iΔx. \nonumber \]
En utilisant\(ρ(x^∗_i)\) pour approximer la densité de la laveuse, nous approximons la masse de la laveuse en
\[m_i≈2πx^∗_iρ(x^∗_i)Δx. \nonumber \]
En additionnant les masses des rondelles, nous voyons que la masse\(m\) de l'ensemble du disque est approximée par
\[m=\sum_{i=1}^nm_i≈\sum_{i=1}^n2πx^∗_iρ(x^∗_i)Δx. \nonumber \]
Nous reconnaissons à nouveau qu'il s'agit d'une somme de Riemann, et prenons la limite comme\(n→∞.\) cela nous donne
\[ \begin{align*} m =\lim_{n→∞}\sum_{i=1}^n2πx^∗_iρ(x^∗_i)Δx \\[4pt] =\int ^r_02πxρ(x)dx. \end{align*}\]
Nous résumons ces résultats dans le théorème suivant.
\(ρ(x)\)Soit une fonction intégrable représentant la densité radiale d'un disque de rayon\(r\). Ensuite, la masse du disque est donnée par
\[m=\int ^r_02πxρ(x)dx. \label{massEq1} \]
\(ρ(x)=\sqrt{x}\)Représentent la densité radiale d'un disque. Calculez la masse d'un disque de rayon 4.
Solution
En appliquant l'équation \ ref {MasseQ1}, nous trouvons
\[ \begin{align*} m =\int ^r_02πxρ(x)dx \nonumber \\[4pt] =\int ^4_02πx\sqrt{x}dx=2π\int ^4_0x^{3/2}dx \nonumber \\[4pt] =2π\dfrac{2}{5}x^{5/2}∣^4_0=\dfrac{4π}{5}[32] \nonumber \\[4pt] =\dfrac{128π}{5}.\nonumber \end{align*}\]
\(ρ(x)=3x+2\)Représentent la densité radiale d'un disque. Calculez la masse d'un disque de rayon 2.
- Allusion
-
Utilisez le processus de l'exemple précédent.
- Solution
-
\(24π\)
Travail effectué par une force
Nous envisageons maintenant le travail. En physique, le travail est lié à la force, qui est souvent définie intuitivement comme une poussée ou une traction sur un objet. Lorsqu'une force déplace un objet, nous disons que la force agit sur l'objet. En d'autres termes, le travail peut être considéré comme la quantité d'énergie nécessaire pour déplacer un objet. Selon la physique, lorsque nous avons une force constante, le travail peut être exprimé comme le produit de la force et de la distance.
Dans le système anglais, l'unité de force est la livre et l'unité de distance est le pied. Le travail est donc exprimé en pieds-livres. Dans le système métrique, les kilogrammes et les mètres sont utilisés. Un newton est la force nécessaire pour accélérer un\(1\) kilogramme de masse à la vitesse de\(1\) m/sec 2. Ainsi, l'unité de travail la plus courante est le newtonomètre. Cette même unité est également appelée joule. Les deux sont définis comme des kilogrammes fois des mètres carrés sur des secondes au carré\((kg⋅m^2/s^2).\)
Lorsque nous avons une force constante, les choses sont assez faciles. Il est cependant rare qu'une force soit constante. Le travail effectué pour comprimer (ou allonger) un ressort, par exemple, varie en fonction de la distance dans laquelle le ressort a déjà été comprimé (ou étiré). Nous examinerons les ressorts plus en détail plus loin dans cette section.
Supposons que nous ayons une force variable\(F(x)\) qui déplace un objet dans une direction positive le long de l'\(x\)axe y d'un point\(a\) à l'autre\(b\). Pour calculer le travail effectué, nous divisons l'intervalle\([a,b]\) et estimons le travail effectué sur chaque sous-intervalle. Donc, pour\(i=0,1,2,…,n\),\(P={x_i}\) soit une partition régulière de l'intervalle\([a,b]\), et pour, pour\(i=1,2,…,n\), choisissez un point arbitraire\(x^∗_i∈[x_{i−1},x_i]\). Pour calculer le travail effectué pour déplacer un objet d'un point\(x_{i−1}\) à un autre\(x_i\), nous supposons que la force est à peu près constante sur l'intervalle et nous l'utilisons\(F(x^∗_i)\) pour approximer la force. Le travail effectué pendant l'intervalle\([x_{i−1},x_i]\) est donc donné par
\[W_i≈F(x^∗_i)(x_{i}−x_{i−1})=F(x^∗_i)Δx. \nonumber \]
Par conséquent, le travail effectué pendant l'intervalle\([a,b]\) est d'environ
\[W=\sum_{i=1}^nW_i≈\sum_{i=1}^nF(x^∗_i)Δx. \nonumber \]
En prenant la limite de cette expression comme suit\(n→∞\), nous obtenons la valeur exacte du travail :
\[ \begin{align*} W =\lim_{n→∞}\sum_{i=1}^nF(x^∗_i)Δx \\[4pt] =\int ^b_aF(x)dx. \end{align*}\]
Ainsi, nous pouvons définir le travail comme suit.
Si une force variable\(F(x)\) déplace un objet dans une direction positive le long de l'\(x\)axe -d' un point\(a\) à l'autre\(b\), le travail effectué sur l'objet est
\[W=\int ^b_aF(x)dx. \label{work} \]
Notez que si elle\(F\) est constante, l'intégrale évalue la formule que nous avons indiquée au début de cette section.\(F⋅(b−a)=F⋅d,\)
Regardons maintenant l'exemple précis du travail effectué pour comprimer ou allonger un ressort. Prenons l'exemple d'un bloc fixé à un ressort horizontal. Le bloc se déplace d'avant en arrière à mesure que le ressort s'étire et se comprime. Bien que dans le monde réel, nous devions tenir compte de la force de friction entre le bloc et la surface sur laquelle il repose, nous ignorons le frottement ici et supposons que le bloc repose sur une surface sans friction. Lorsque le ressort est à sa longueur naturelle (au repos), on dit que le système est en équilibre. Dans cet état, le ressort n'est ni allongé ni comprimé et, dans cette position d'équilibre, le bloc ne bouge pas tant qu'une certaine force n'est pas introduite. Nous orientons le système de manière à ce qu'il\(x=0\) corresponde à la position d'équilibre (Figure\(\PageIndex{4}\)).
Selon la loi de Hooke, la force requise pour comprimer ou étirer un ressort à partir d'une position d'équilibre est donnée par\(F(x)=kx\), pour une certaine constante\(k\). La valeur de k dépend des caractéristiques physiques du ressort. La constante\(k\) est appelée constante de ressort et est toujours positive. Nous pouvons utiliser ces informations pour calculer le travail effectué pour comprimer ou allonger un ressort, comme le montre l'exemple suivant.
Supposons qu'il faille une force de\(10\) N (dans le sens négatif) pour comprimer un ressort\(0.2\) m à partir de la position d'équilibre. Combien de travail est effectué pour étirer le ressort\(0.5\) m à partir de la position d'équilibre ?
Solution
Trouvez d'abord la constante du ressort,\(k\). Quand\(x=−0.2\),\(F(x)=−10,\) nous le savons
\[ \begin{align*} F(x) =kx \\[4pt] −10 =k(−0.2) \\[4pt] k =50 \end{align*}\]
et\(F(x)=50x.\) ensuite, pour calculer le travail, nous intégrons la fonction de force, en obtenant
\[\begin{align*} W = \int ^b_aF(x)dx \\[4pt] =\int ^{0.5}_050 x \,dx \\[4pt] =\left. 25x^2 \right|^{0.5}_0 \\[4pt] =6.25. \end{align*}\]
Le travail effectué pour étirer le ressort est\(6.25\) J.
Supposons qu'il faille une force de\(8\) lb pour étirer un ressort\(6\) à partir de la position d'équilibre. Combien de travail est effectué pour étirer le ressort à\(1\) pieds depuis la position d'équilibre ?
- Allusion
-
Utilisez le processus de l'exemple précédent. Soyez prudent avec les unités.
- Solution
-
\(8\)pied-lb
Travail effectué dans le domaine du pompage
Pensez au travail effectué pour pomper de l'eau (ou un autre liquide) hors d'un réservoir. Les problèmes de pompage sont un peu plus compliqués que les problèmes de ressort car de nombreux calculs dépendent de la forme et de la taille du réservoir. De plus, au lieu de nous préoccuper du travail effectué pour déplacer une seule masse, nous examinons le travail effectué pour déplacer un volume d'eau, et il faut plus de travail pour déplacer l'eau du fond du réservoir que pour déplacer l'eau du haut du réservoir.
Nous examinons le processus dans le contexte d'un réservoir cylindrique, puis examinons quelques exemples utilisant des réservoirs de différentes formes. Supposons qu'un réservoir cylindrique de rayon\(4\)\(10\) m et de hauteur m soit rempli jusqu'à une profondeur de 8 m. Combien de travail faut-il pour pomper toute l'eau par le bord supérieur du réservoir ?
La première chose à faire est de définir un cadre de référence. Nous laissons\(x\) représenter la distance verticale sous le sommet du réservoir. C'est-à-dire que nous orientons l'\(x\)axe -verticalement, l'origine en haut du réservoir et la direction descendante étant positive (Figure\(\PageIndex{5}\)).
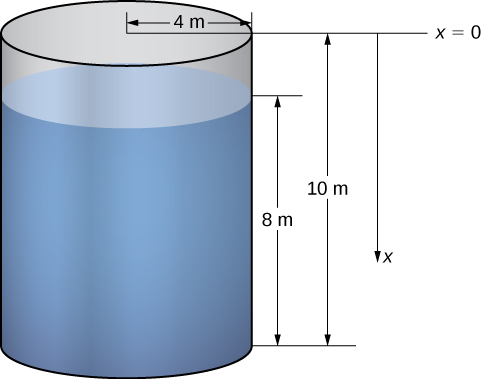
À l'aide de ce système de coordonnées, l'eau s'étend de\(x=2\) à\(x=10\). Par conséquent, nous divisons l'intervalle\([2,10]\) et examinons le travail requis pour soulever chaque « couche » d'eau individuelle. Donc, pour\(i=0,1,2,…,n\),\(P={x_i}\) soit une partition régulière de l'intervalle\([2,10]\), et pour, pour\(i=1,2,…,n\), choisissez un point arbitraire\(x^∗_i∈[x_{i−1},x_i]\). La figure\(\PageIndex{6}\) montre une couche représentative.
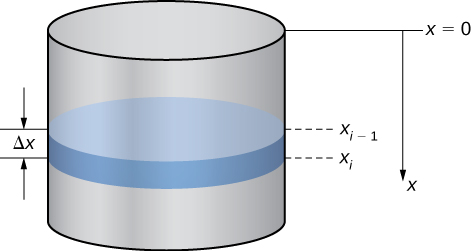
En cas de problèmes de pompage, la force requise pour soulever l'eau vers le haut du réservoir est la force requise pour surmonter la gravité, elle est donc égale au poids de l'eau. Étant donné que la masse volumique de l'eau est\(9800 \, \text{N/m}^3\), ou\(62.4\,\text{lb/ft}^3\), le calcul du volume de chaque couche nous donne le poids. Dans ce cas, nous avons
\[V=π(4)^2Δx=16πΔx. \nonumber \]
Ensuite, la force nécessaire pour soulever chaque couche est
\[F=9800⋅16πΔx=156,800πΔx. \nonumber \]
Notez que cette étape devient un peu plus difficile si nous avons un réservoir non cylindrique. Nous examinons un réservoir non cylindrique dans l'exemple suivant.
Nous devons également connaître la distance à laquelle l'eau doit être soulevée. Sur la base de notre choix de systèmes de coordonnées, nous pouvons utiliser\(x^∗_i\) comme approximation de la distance à laquelle la couche doit être soulevée. Ensuite, le travail pour soulever la\(i^{\text{th}}\) couche d'eau\(W_i\) est d'environ
\[W_i≈156,800πx^∗_iΔx. \nonumber \]
En ajoutant le travail pour chaque couche, nous voyons que le travail approximatif pour vider le réservoir est donné par
\[ \begin{align*} W =\sum_{i=1}^nW_i \\[4pt] ≈\sum_{i=1}^n156,800πx^∗_iΔx.\end{align*}\]
Il s'agit d'une somme de Riemann, donc en prenant la limite au\(n→∞,\) fur et à mesure
\[ \begin{align*} W =\lim_{n→∞}\sum^n_{i=1}156,800πx^∗_iΔx \\[4pt] = 156,800π\int ^{10}_2xdx \\[4pt] =156,800π \left( \dfrac{x^2}{2}\right)\bigg|^{10}_2=7,526,400π≈23,644,883. \end{align*}\]
Le travail requis pour vider le réservoir est d'environ 23 650 000 J.
Pour les problèmes de pompage, les calculs varient en fonction de la forme du réservoir ou du récipient. La stratégie de résolution de problèmes suivante décrit un processus étape par étape pour résoudre les problèmes de pompage.
- Esquissez une image du réservoir et sélectionnez un cadre de référence approprié.
- Calculez le volume d'une couche d'eau représentative.
- Multipliez le volume par la masse volumique de l'eau pour obtenir la force.
- Calculez la distance à laquelle la couche d'eau doit être soulevée.
- Multipliez la force et la distance pour obtenir une estimation du travail nécessaire pour soulever la couche d'eau.
- Somme le travail requis pour soulever toutes les couches. Cette expression est une estimation du travail requis pour pomper la quantité d'eau souhaitée, et elle se présente sous la forme d'une somme de Riemann.
- Prenez la limite au fur\(n→∞\) et à mesure et évaluez l'intégrale résultante pour obtenir le travail exact requis pour pomper la quantité d'eau souhaitée.
Nous appliquons maintenant cette stratégie de résolution de problèmes dans un exemple avec un réservoir non cylindrique.
Supposons un réservoir en forme de cône inversé, avec une hauteur en\(12\) pieds et un rayon de base en\(4\) pieds. Le réservoir est plein au départ et de l'eau est pompée sur le bord supérieur du réservoir jusqu'à ce que la hauteur de l'eau restant dans le réservoir soit de\(4\) pieds. Combien de travail faut-il pour pomper cette quantité d'eau ?
Solution
Le réservoir est représenté sur la figure\(\PageIndex{7}\). Comme nous l'avons fait dans l'exemple avec le réservoir cylindrique, nous orientons\(x\) l'axe -verticalement, l'origine en haut du réservoir et la direction vers le bas étant positive (étape 1).
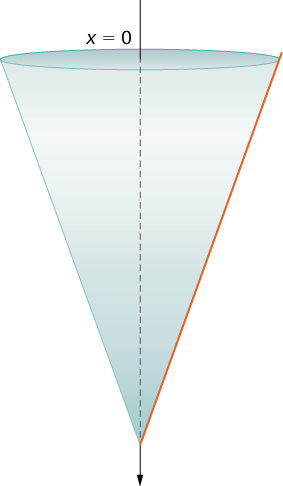
Le réservoir commence plein et se termine\(4\) alors qu'il reste un mètre d'eau. Par conséquent, en fonction du cadre de référence que nous avons choisi, nous devons diviser l'intervalle\([0,8]\). Ensuite, pour\(i=0,1,2,…,n\),\(P={x_i}\) soit une partition régulière de l'intervalle\([0,8]\), et pour, pour\(i=1,2,…,n\), choisissez un point arbitraire\(x^∗_i∈[x_{i−1},x_i]\). Nous pouvons approximer le volume d'une couche à l'aide d'un disque, puis utiliser des triangles similaires pour déterminer le rayon du disque (Figure\(\PageIndex{8}\)).
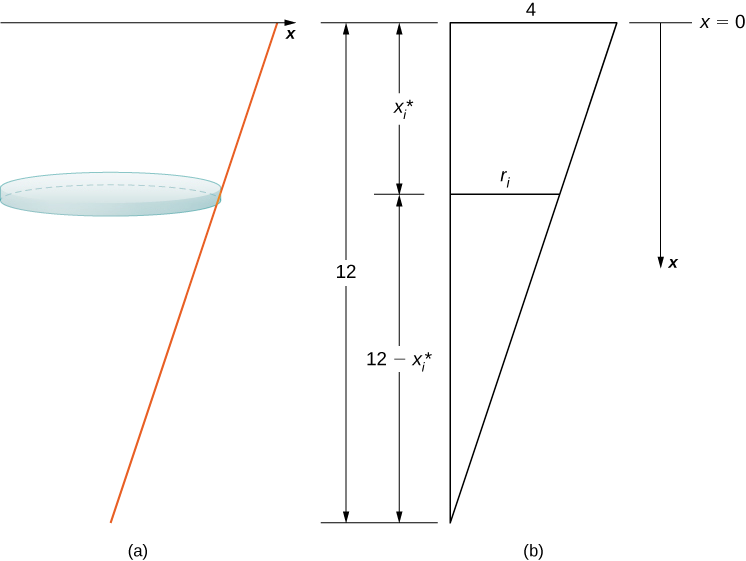
À partir des propriétés de triangles similaires, nous avons
\[ \begin{align*} \dfrac{r_i}{12−x^∗_i} =\dfrac{4}{12} \tag{step 1} =\dfrac{1}{3} \\[4pt] 3r_i =12−x^∗_i \\[4pt] r_i =\dfrac{12−x^∗_i}{3} \\[4pt] =4−\dfrac{x^∗_i}{3}. \end{align*} \]
Ensuite, le volume du disque est
\[V_i=π \left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx. \tag{step 2} \]
La densité pondérale de l'eau est de\(62.4\) lb/ft 3, de sorte que la force nécessaire pour soulever chaque couche est d'environ
\[F_i≈62.4π\left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx \tag{step 3} \]
Sur la base du diagramme, la distance à laquelle l'eau doit être soulevée est d'environ\(x^∗_i\) pieds (étape 4), de sorte que le travail approximatif nécessaire pour soulever la couche est
\[W_i≈62.4πx^∗_i\left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx. \tag{step 5} \]
En additionnant le travail requis pour soulever toutes les couches, nous obtenons une valeur approximative du travail total :
\[W=\sum_{i=1}^nW_i≈\sum_{i=1}^n62.4πx^∗_i \left(4−\dfrac{x^∗_i}{3}\right)^2\,Δx. \tag{step 6} \]
Prendre la limite au\(n→∞,\) fur et à mesure
\[ \begin{align*} W =\lim_{n→∞}\sum^n_{i=1}62.4πx^∗_i(4−\dfrac{x^∗_i}{3})^2Δx \\[4pt] = \int ^8_062.4πx \left(4−\dfrac{x}{3}\right)^2dx \\[4pt] = 62.4π\int ^8_0x \left(16−\dfrac{8x}{3}+\dfrac{x^2}{9}\right)\,dx=62.4π\int ^8_0 \left(16x−\dfrac{8x^2}{3}+\dfrac{x^3}{9}\right)\,dx \\[4pt] =62.4π\left[8x^2−\dfrac{8x^3}{9}+\dfrac{x^4}{36}\right]\bigg|^8_0=10,649.6π≈33,456.7. \end{align*}\]
Il faut environ\(33,450\) ft-lb de travail pour vider le réservoir au niveau souhaité.
Un réservoir a la forme d'un cône inversé, avec une hauteur en\(10\) pieds et un rayon de base de 6 pieds. Le réservoir est rempli à une profondeur de 8 pieds au départ, et de l'eau est pompée sur le bord supérieur du réservoir jusqu'à ce qu'il reste 3 pieds d'eau dans le réservoir. Combien de travail faut-il pour pomper cette quantité d'eau ?
- Allusion
-
Utilisez le processus de l'exemple précédent.
- Solution
-
Environ\(43,255.2\) ft-lb
Force et pression hydrostatiques
Dans cette dernière section, nous examinons la force et la pression exercées sur un objet immergé dans un liquide. Dans le système anglais, la force est mesurée en livres. Dans le système métrique, il est mesuré en newtons. La pression est la force par unité de surface, donc dans le système anglais, nous avons des livres par pied carré (ou, peut-être plus communément, des livres par pouce carré, notées psi). Dans le système métrique, nous avons des newtons par mètre carré, également appelés pascals.
Commençons par le cas simple d'une plaque de surface\(A\) immergée horizontalement dans l'eau à une profondeur s (Figure\(\PageIndex{9}\)). Ensuite, la force exercée sur la plaque est simplement le poids de l'eau au-dessus de celle-ci, qui est donné par\(F=ρAs\), où\(ρ\) est la densité pondérale de l'eau (poids par unité de volume). Pour déterminer la pression hydrostatique, c'est-à-dire la pression exercée par l'eau sur un objet immergé, nous divisons la force par la surface. Donc, la pression est là\(p=F/A=ρs\).
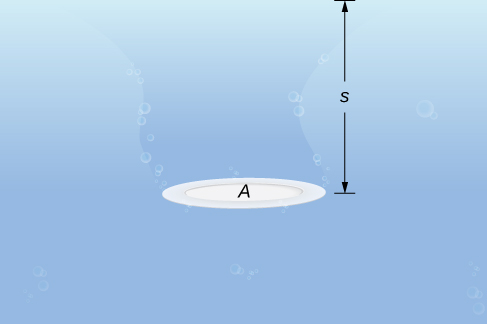
Selon le principe de Pascal, la pression à une profondeur donnée est la même dans toutes les directions, peu importe que la plaque soit immergée horizontalement ou verticalement. Donc, tant que nous connaissons la profondeur, nous connaissons la pression. Nous pouvons appliquer le principe de Pascal pour déterminer la force exercée sur des surfaces, telles que des barrages, qui sont orientées verticalement. Nous ne pouvons pas appliquer la formule\(F=ρAs\) directement, car la profondeur varie d'un point à l'autre sur une surface orientée verticalement. Ainsi, comme nous l'avons fait à de nombreuses reprises auparavant, nous formons une partition, une somme de Riemann et, finalement, une intégrale définie pour calculer la force.
Supposons qu'une fine plaque soit immergée dans l'eau. Nous choisissons notre cadre de référence de telle sorte que l'\(x\)axe -soit orienté verticalement, la direction descendante étant positive et le point\(x=0\) correspondant à un point de référence logique. \(s(x)\)Notons la profondeur au point x. Notez que nous laissons souvent\(x=0\) correspondre à la surface de l'eau. Dans ce cas, la profondeur à tout moment est simplement donnée par\(s(x)=x\). Cependant, dans certains cas, il se peut que nous souhaitions sélectionner un point de référence différent pour\(x=0\), nous procédons donc au développement dans le cas plus général. Enfin,\(w(x)\) notons la largeur de la plaque à la pointe\(x\).
Supposons que le bord supérieur de la plaque est pointu\(x=a\) et que le bord inférieur de la plaque est pointu\(x=b\). Ensuite, pour\(i=0,1,2,…,n\),\(P={x_i}\) soit une partition régulière de l'intervalle\([a,b]\), et pour, pour\(i=1,2,…,n\), choisissez un point arbitraire\(x^∗_i∈[x_{i−1},x_i]\). La cloison divise la plaque en plusieurs fines bandes rectangulaires (Figure\(\PageIndex{10}\)).
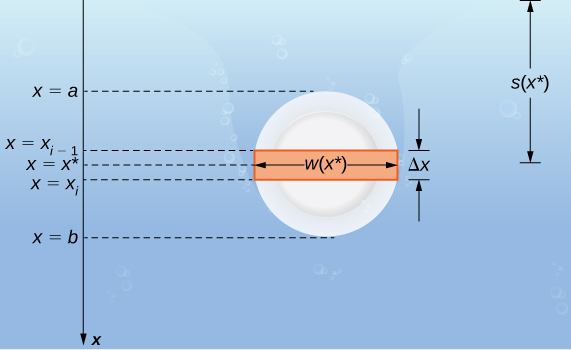
Estimons maintenant la force sur une bande représentative. Si la bande est suffisamment fine, on peut la traiter comme si elle était à une profondeur constante\(s(x^∗_i)\). Nous avons alors
\[F_i=ρAs=ρ[w(x^∗_i)Δx]s(x^∗_i). \nonumber \]
En additionnant les forces, on obtient une estimation de la force sur la plaque :
\[F≈\sum_{i=1}^nF_i=\sum_{i=1}^nρ[w(x^∗_i)Δx]s(x^∗_i). \nonumber \]
Il s'agit d'une somme de Riemann, donc le fait de prendre la limite nous donne la force exacte. Nous obtenons
\[F=\lim_{n→∞}\sum_{i=1}^nρ[w(x^∗_i)Δx]s(x^∗_i)=\int ^b_aρw(x)s(x)dx. \label{eqHydrostatic} \]
L'évaluation de cette intégrale nous donne la force sur la plaque. Nous résumons cela dans la stratégie de résolution de problèmes suivante.
- Esquissez une image et sélectionnez un cadre de référence approprié. (Notez que si nous sélectionnons un cadre de référence autre que celui utilisé précédemment, nous devrons peut-être ajuster l'équation \ ref {EQHydrostatic} en conséquence.)
- Déterminez les fonctions de profondeur et de largeur,\(s(x)\) et\(w(x).\)
- Déterminez la masse volumique du liquide avec lequel vous travaillez. La densité pondérale de l'eau est\(62.4 \,\text{lb/ft}^3\), ou\(9800 \,\text{N/m}^3\).
- Utilisez l'équation pour calculer la force totale.
Un abreuvoir de 15 pieds de long a des extrémités en forme de triangles isocèles inversés, avec une base de 8 pieds et une hauteur de 3 pieds. Déterminez la force exercée sur une extrémité de l'abreuvoir si celui-ci est plein d'eau.
Solution
La figure\(\PageIndex{11}\) montre le creux et une vue plus détaillée d'une extrémité.
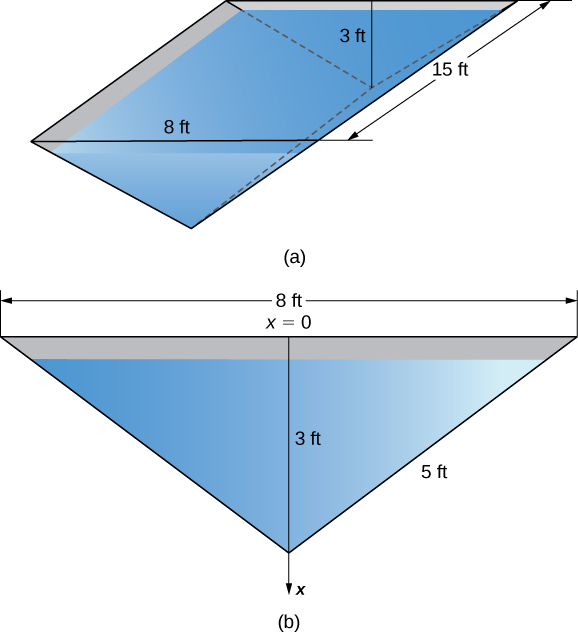
Sélectionnez un cadre de référence dont l'\(x\)axe est orienté verticalement et dont la direction descendante est positive. Sélectionnez le haut du creux comme point correspondant à\(x=0\) (étape 1). La fonction de profondeur est donc\(s(x)=x\). En utilisant des triangles similaires, nous le voyons\(w(x)=8−(8/3)x\) (étape 2). Maintenant, la densité pondérale de l'eau est\(62.4 \,\text{lb/ft}^3\) (étape 3), donc en appliquant l'équation \ ref {EQHydrostatic}, nous obtenons
\[ \begin{align*} F =\int ^b_aρw(x)s(x)dx \\[4pt] = \int ^3_062.4 \left(8−\dfrac{8}{3}x\right) x \,dx=62.4\int ^3_0 \left(8x−\dfrac{8}{3}x^2 \right)dx \\[4pt] = \left.62.4 \left[4x^2−\dfrac{8}{9}x^3\right]\right|^3_0=748.8. \end{align*}\]
L'eau exerce une force de 748,8 livres sur l'extrémité de la cuvette (étape 4).
Un abreuvoir de 12 m de long a des extrémités en forme de triangles isocèles inversés, avec une base de 6 m et une hauteur de 4 m. Déterminez la force exercée sur une extrémité de l'abreuvoir si l'abreuvoir est plein d'eau.
- Allusion
-
Suivez la stratégie de résolution de problèmes et le processus de l'exemple précédent.
- Solution
-
\(156,800\)N
Nous revenons maintenant au barrage Hoover, mentionné au début de ce chapitre. Le barrage lui-même est voûté plutôt que plat, mais nous allons faire quelques hypothèses simplificatrices pour nous aider dans les calculs. Supposons que la face du barrage Hoover ait la forme d'un trapèze isocèle avec une base inférieure de 750 pieds, une base supérieure de 1 250 pieds et une hauteur de 750 pieds (voir la figure suivante).

Lorsque le réservoir est plein, la profondeur maximale du lac Mead est d'environ 530 pieds et la surface du lac se trouve à environ 10 pieds sous le sommet du barrage (voir la figure suivante).
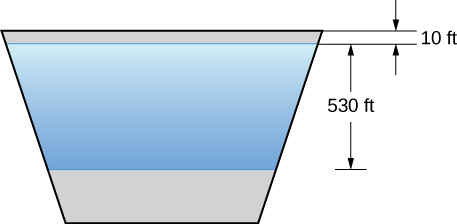
- Déterminez la force exercée sur la face du barrage lorsque le réservoir est plein.
- Le sud-ouest des États-Unis connaît une sécheresse et la surface du lac Mead se trouve à environ 125 pieds plus bas que ce qu'elle serait si le réservoir était plein. Quelle est la force exercée sur la face du barrage dans ces circonstances ?
Solution :
un.
Nous commençons par établir un cadre de référence. Comme d'habitude, nous choisissons d'orienter l'\(x\)axe -verticalement, la direction vers le bas étant positive. Cette fois, cependant, nous allons laisser\(x=0\) représenter le sommet du barrage, plutôt que la surface de l'eau. Lorsque le réservoir est plein, la surface de l'eau se trouve\(10\) pieds sous le sommet du barrage, donc\(s(x)=x−10\) (voir la figure suivante).

Pour trouver la fonction de largeur, nous nous tournons à nouveau vers des triangles similaires, comme indiqué dans la figure ci-dessous.
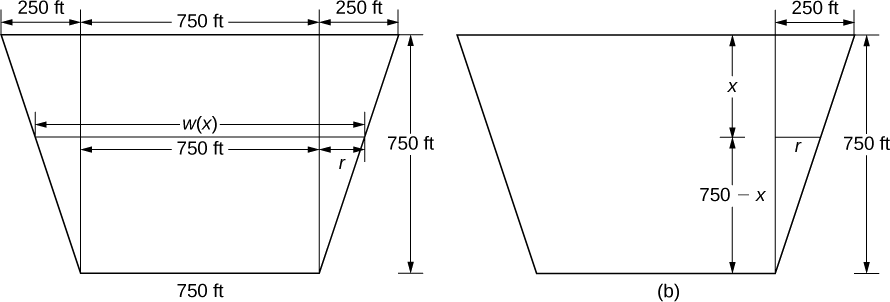
Sur la figure, nous le voyons\(w(x)=750+2r\). En utilisant les propriétés de triangles similaires, nous obtenons\(r=250−(1/3)x\). Ainsi,
\[w(x)=1250−\dfrac{2}{3}x \tag{step 2} \]
En utilisant une masse volumique de\(62.4\) lb/ft 3 (étape 3) et en appliquant l'équation \ ref {EQHydrostatic}, nous obtenons
\ [\ begin {align*} F = \ int^b_a ρw (x) s (x) \, dx \ \ [4 points]
= \ int ^ {540} _ {10} 62,4 \ left (1250− \ dfrac {2} {3} x \ right) (x−10) \, dx \ \ [4 points]
=62,4 \ int ^ {540} _ {10} − \ dfrac {2} {3} [x^2−1885x+18750] \, dx \ \ [4 points]
=−62,4 \ left (\ dfrac {2} {3} \ right) \ left [\ dfrac {x^3} {3} − \ dfrac {1885x^2} {2} +18750x \ right] \ bigg|^ {540} _ {10} ≈ 8 832 245 000 \, \ text {lb} =4 416 122,5 \, \ text {t}. \ end {align*} \]
Notez le passage des livres aux tonnes (\(2000\)lb =\(1\) tonne) (étape 4). Cela modifie notre fonction de\(s(x)\) profondeur et nos limites d'intégration. Nous l'avons fait\(s(x)=x−135\). La limite inférieure d'intégration est de 135. La limite supérieure demeure\(540\). En évaluant l'intégrale, nous obtenons
\ [\ begin {align*} F = \ int^b_aρw (x) s (x) \, dx \ \ [4 points]
= \ int ^ {540} _ {135} 62,4 \ left (1250− \ dfrac {2} {3} x \ right) (x−135) \, dx \ \ [4 points]
=−62,4 (\ dfrac {2} {3}) \ int ^ {540} _ {135} (x−1875) (x−135) \, dx=−62,4 \ left (\ dfrac {2} {3} \ right) \ int ^ {540} _ {135} (x^2−2010x+253125) \, dx \ \ [4 points]
=−62,4 \ left (\ dfrac {2} {3} \ right) \ left [\ dfrac {x^3} {3} −1005x^2+253125x \ right] \ bigg|^ {540} _ {135} ÷ 5 015 230 000 \, \ text {lb} =2 507 615 \, \ text {t}. \ end {align*} \]
Lorsque le réservoir est à son niveau moyen, la surface de l'eau se trouve à environ 50 pieds en dessous de ce qu'elle serait si le réservoir était plein. Quelle est la force exercée sur la face du barrage dans ces circonstances ?
- Allusion
-
Modifiez la fonction de profondeur\(s(x),\) et les limites de l'intégration.
- Solution
-
Environ 7 164 520 000 livres ou 3 582 260 t
Concepts clés
- Plusieurs applications physiques de l'intégrale définie sont courantes en ingénierie et en physique.
- Des intégrales définies peuvent être utilisées pour déterminer la masse d'un objet si sa fonction de densité est connue.
- Le travail peut également être calculé en intégrant une fonction de force ou en neutralisant la force de gravité, comme dans le cas d'un problème de pompage.
- Des intégrales définies peuvent également être utilisées pour calculer la force exercée sur un objet immergé dans un liquide.
Équations clés
- Masse d'un objet unidimensionnel
\( \displaystyle m=\int ^b_aρ(x)dx\)
- Masse d'un objet circulaire
\(\displaystyle m=\int ^r_02πxρ(x)dx\)
- Travail effectué sur un objet
\(\displaystyle W=\int ^b_aF(x)dx\)
- Force hydrostatique sur une plaque
\(\displaystyle F=\int ^b_aρw(x)s(x)dx\)
Lexique
- fonction de densité
- une fonction de densité décrit la façon dont la masse est distribuée dans un objet ; il peut s'agir d'une densité linéaire, exprimée en termes de masse par unité de longueur ; d'une densité de surface, exprimée en termes de masse par unité de surface ; ou d'une densité volumique, exprimée en termes de masse par unité de volume ; le poids-densité est également utilisé pour décrire poids (plutôt que masse) par unité de volume
- Loi de Hooke
- cette loi stipule que la force requise pour comprimer (ou allonger) un ressort est proportionnelle à la distance à laquelle le ressort a été comprimé (ou étiré) par rapport à l'équilibre ; en d'autres termes\(F=kx\), où\(k\) est une constante
- pression hydrostatique
- la pression exercée par l'eau sur un objet immergé
- travail
- la quantité d'énergie nécessaire pour déplacer un objet ; en physique, lorsqu'une force est constante, le travail est exprimé comme le produit de la force et de la distance


