6.1 : Zones entre les courbes

Last updated
Save as PDF

Page ID: 197282

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objectifs d'apprentissage

Déterminez l'aire d'une région située entre deux courbes en intégrant par rapport à la variable indépendante.
Détermine l'aire d'une région composée.
Déterminez l'aire d'une région située entre deux courbes en effectuant une intégration par rapport à la variable dépendante.

Dans Introduction à l'intégration, nous avons développé le concept de l'intégrale définie pour calculer l'aire sous une courbe sur un intervalle donné. Dans cette section, nous étendons cette idée pour calculer la superficie de régions plus complexes. Nous commençons par déterminer l'aire entre deux courbes qui sont des fonctions de$\displaystyle x$, en commençant par le cas simple où une valeur de fonction est toujours supérieure à l'autre. Nous examinons ensuite les cas où les graphes des fonctions se croisent. Enfin, nous examinons comment calculer l'aire entre deux courbes qui sont des fonctions de$\displaystyle y$.

Aire d'une région comprise entre deux courbes

Les fonctions$\displaystyle f(x)$ Let and$\displaystyle g(x)$ Be sont continues sur un intervalle$\displaystyle [a,b]$ tel que$\displaystyle f(x)≥g(x)$ activé$\displaystyle [a,b]$. Nous voulons trouver l'aire entre les graphes des fonctions, comme indiqué sur la figure$\PageIndex{1}$.

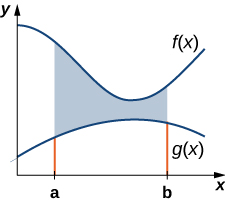
Cette figure est un graphique du premier quadrant. Le graphique comporte deux courbes. La courbe supérieure est étiquetée « f (x) » et la courbe inférieure est étiquetée « g (x) ». Il existe deux limites sur l'axe des abscisses étiquetées a et b. Il existe une zone ombrée entre les deux courbes délimitée par des lignes à x=a et x=b. — Figure$\PageIndex{1}$ : L'aire entre les graphes de deux fonctions$\displaystyle f(x)$ et$\displaystyle g(x)$, sur l'intervalle$\displaystyle [a,b]$

Comme nous l'avons fait auparavant, nous allons partitionner l'intervalle sur l'axe des abscisses et approximer l'aire entre les graphes des fonctions avec des rectangles. Donc, pour$\displaystyle i=0,1,2,…,n$,$\displaystyle P={x_i}$ soyons une partition régulière de$\displaystyle [a,b]$. Ensuite, pour$\displaystyle i=1,2,…,n,$ choisir un point$\displaystyle x^∗_i∈[x_{i−1},x_i]$, et sur chaque intervalle,$\displaystyle [x_{i−1},x_i]$ construisez un rectangle qui s'étend verticalement de$\displaystyle g(x^∗_i)$ à$\displaystyle f(x^∗_i)$. La figure$\PageIndex{2a}$ montre les rectangles lorsqu'elle$\displaystyle x^∗_i$ est sélectionnée comme extrémité gauche de l'intervalle et$\displaystyle n=10$. La figure$\PageIndex{2b}$ montre un rectangle représentatif en détail.

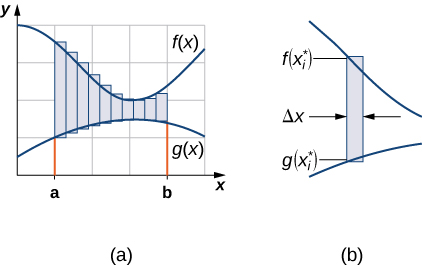
Cette figure comporte trois graphiques. Le premier graphique comporte deux courbes, l'une au-dessus de l'autre. Entre les courbes se trouve un rectangle. Le haut du rectangle se trouve sur la courbe supérieure intitulée « f (x*) » et le bas du rectangle se trouve sur la courbe inférieure et est étiqueté « g (x*) ». Le deuxième graphique, intitulé « (a) », comporte deux courbes. La courbe supérieure est étiquetée « f (x) » et la courbe inférieure est étiquetée « g (x) ». Il existe deux limites sur l'axe des abscisses, étiquetées a et b. Il existe une zone ombrée entre les deux courbes délimitée par des lignes à x=a et x=b. Le troisième graphe, intitulé « (b) », comporte deux courbes l'une au-dessus de l'autre. La première courbe est étiquetée « f (x*) » et la courbe inférieure est étiquetée « g (x*) ». Il y a un rectangle ombré entre les deux. La largeur du rectangle est étiquetée « delta x ». — Figure$\PageIndex{2}$ : (a) Nous pouvons approximer l'aire entre les graphes de deux fonctions,$\displaystyle f(x)$ et$\displaystyle g(x)$, avec des rectangles. (b) L'aire d'un rectangle typique va d'une courbe à l'autre.

La hauteur de chaque rectangle individuel est$\displaystyle f(x^∗_i)−g(x^∗_i)$ et la largeur de chaque rectangle est$\displaystyle Δx$. En ajoutant les aires de tous les rectangles, nous voyons que la zone entre les courbes est approximée par

\[\displaystyle A≈\sum_{i=1}^n[f(x^∗_i)−g(x^∗_i)]Δx. \nonumber \]

Il s'agit d'une somme de Riemann, donc nous prenons la limite au fur$\displaystyle n→∞$ et à mesure

\[\displaystyle A=\lim_{n→∞}\sum_{i=1}^n[f(x^∗_i)−g(x^∗_i)]Δx=\int ^b_a[f(x)−g(x)]dx. \nonumber \]

Ces résultats sont résumés dans le théorème suivant.

Trouver l'aire entre deux courbes

Les fonctions$\displaystyle f(x)$ Let et$\displaystyle g(x)$ Be sont continues de telle sorte que$\displaystyle f(x)≥g(x)$ sur un intervalle [$\displaystyle a,b]$. Soit R la région délimitée au-dessus par le graphique de$\displaystyle f(x)$, en dessous par le graphique de$\displaystyle g(x)$, et à gauche et à droite par les lignes$\displaystyle x=a$ et$\displaystyle x=b$, respectivement. Ensuite, la surface de$\textbf{R}$ est donnée par

\[A=\int ^b_a[f(x)−g(x)]dx. \nonumber \]

Nous appliquons ce théorème dans l'exemple suivant.

Exemple$\PageIndex{1}$: Finding the Area of a Region between Two Curves I

S'il s'$\textbf{R}$agit de la région délimitée en haut par le graphe de la fonction$\displaystyle f(x)=x+4$ et en dessous par le graphique de la fonction$\displaystyle g(x)=3−\dfrac{x}{2}$ sur l'intervalle$\displaystyle [1,4]$, trouvez l'aire de la région$\textbf{R}$.

Solution

La région est illustrée dans la figure suivante.

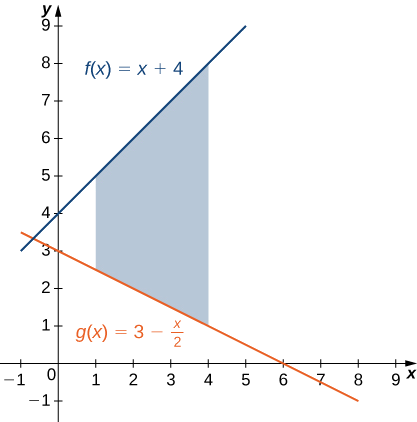
Cette figure comporte deux graphiques linéaires dans le premier quadrant. Ce sont les fonctions f (x) = x+4 et g (x) = 3-x/2. Entre ces lignes se trouve une zone ombrée, délimitée au-dessus par f (x) et au-dessous par g (x). La zone ombrée est comprise entre x=1 et x=4. — Figure$\PageIndex{3}$ : Une région située entre deux courbes est illustrée, où l'une des courbes est toujours plus grande que l'autre.

Nous avons

\[ \begin{align*} A =\int ^b_a[f(x)−g(x)]\,dx \\[4pt] =\int ^4_1[(x+4)−(3−\dfrac{x}{2})]\,dx=\int ^4_1\left[\dfrac{3x}{2}+1\right]\,dx \\[4pt] =[\dfrac{3x^2}{4}+x]\bigg|^4_1=(16−\dfrac{7}{4})=\dfrac{57}{4}. \end{align*}\]

La superficie de la région est$\displaystyle \dfrac{57}{4}units^2$.

Exercice$\PageIndex{1}$

Si$\textbf{R}$ c'est la région délimitée par les graphes des fonctions$\displaystyle f(x)=\dfrac{x}{2}+5$ et$\displaystyle g(x)=x+\dfrac{1}{2}$ sur l'intervalle$\displaystyle [1,5]$, trouvez l'aire de la région$\textbf{R}$.

Allusion: Tracez les fonctions pour déterminer quel graphe de fonction forme la limite supérieure et lequel forme la limite inférieure, puis suivez le processus utilisé dans l'exemple.

Réponse: $\displaystyle 12$unités ²

Dans Exemple$\PageIndex{1}$, nous avons défini l'intervalle d'intérêt dans le cadre de l'énoncé du problème. Cependant, nous voulons souvent définir notre intervalle d'intérêt en fonction de l'intersection des graphes des deux fonctions. Ceci est illustré dans l'exemple suivant.

Exemple$\PageIndex{2}$: Finding the Area of a Region between Two Curves II

S'il s'$\textbf{R}$agit de la région délimitée en haut par le graphe de la fonction$\displaystyle f(x)=9−(x/2)^2$ et en dessous par le graphique de la fonction$\displaystyle g(x)=6−x$, trouvez l'aire de la région$\textbf{R}$.

Solution

La région est illustrée dans la figure suivante.

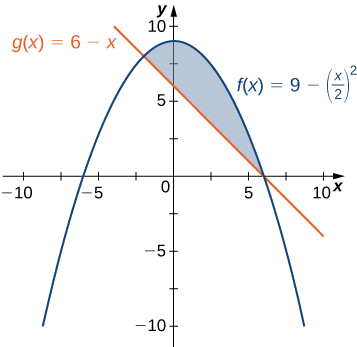
Cette figure comporte deux graphiques dans le premier quadrant. Ce sont les fonctions f (x) = 9- (x/2) ^2 et g (x) = 6-x. Entre ces graphes, une parabole inversée et une droite se trouve une région ombrée, délimitée en haut par f (x) et en dessous par g (x). — Figure$\PageIndex{4}$ : Ce graphique montre la région située en dessous du graphique$\displaystyle f(x)$ et au-dessus du graphique de$\displaystyle g(x).$

Nous devons d'abord calculer où les graphes des fonctions se croisent. $\displaystyle f(x)=g(x),$Nous obtenons un réglage

\[ \begin{align*} \displaystyle f(x) =g(x) \\[4pt] 9−(\dfrac{x}{2})^2 =6−x\\[4pt] 9−\dfrac{x^2}{4} =6−x\\[4pt] 36−x^2 =24−4x\\[4pt] x^2−4x−12 =0\\[4pt] (x−6)(x+2) =0. \end{align*}\]

Les graphes des fonctions se croisent lorsque$\displaystyle x=6$$\displaystyle x=−2,$ nous voulons intégrer de$\displaystyle −2$ à$\displaystyle 6$. Puisque$\displaystyle f(x)≥g(x)$ pour$\displaystyle −2≤x≤6,$ nous obtenons

\[\begin{align*} \displaystyle A =\int ^b_a[f(x)−g(x)]\,dx \\ =\int ^6_{−2} \left[9−(\dfrac{x}{2})^2−(6−x)\right]\,dx \\ =\int ^6_{−2}\left[3−\dfrac{x^2}{4}+x\right]\,dx \\ = \left. \left[3x−\dfrac{x^3}{12}+\dfrac{x^2}{2}\right] \right|^6_{−2}=\dfrac{64}{3}. \end{align*}\]

La superficie de la région est constituée$\displaystyle 64/3$ d'unités ².

Exercice$\PageIndex{2}$

S'il s'$\textbf{R}$agit de la région délimitée en haut par le graphe de la fonction$\displaystyle f(x)=x$ et en dessous par le graphique de la fonction$\displaystyle g(x)=x^4$, trouvez l'aire de la région$\textbf{R}$.

Allusion: Utilisez le processus décrit dans Example$\PageIndex{2}$.

Réponse: $\displaystyle \dfrac{3}{10}$unité ²

Zones de régions composées

Jusqu'à présent, nous avons demandé tout l'$\displaystyle f(x)≥g(x)$intervalle d'intérêt, mais que se passerait-il si nous voulions examiner les régions délimitées par les graphes de fonctions qui se croisent ? Dans ce cas, nous modifierons le processus que nous venons de développer en utilisant la fonction de valeur absolue.

Déterminer l'aire d'une région entre des courbes qui se croisent

Les fonctions$\displaystyle f(x)$ Let and$\displaystyle g(x)$ Be sont continues sur un intervalle$\displaystyle [a,b]$. $\textbf{R}$Dénotons la région située entre les graphes de$\displaystyle f(x)$ et$\displaystyle g(x)$, et sommes délimitée à gauche et à droite par les lignes$\displaystyle x=a$ et$\displaystyle x=b$, respectivement. Ensuite, la surface de$\textbf{R}$ est donnée par

\[A=\int ^b_a|f(x)−g(x)|dx. \nonumber \]

En pratique, l'application de ce théorème nécessite de diviser l'intervalle$\displaystyle [a,b]$ et d'évaluer plusieurs intégrales, en fonction de la valeur de la fonction qui est la plus élevée sur une partie donnée de l'intervalle. Nous étudions ce processus dans l'exemple suivant.

Exemple$\PageIndex{3}$: Finding the Area of a Region Bounded by Functions That Cross

Si$\textbf{R}$ c'est la région située entre les graphes des fonctions$\displaystyle f(x)=\sin x $ et$\displaystyle g(x)=\cos x$ sur l'intervalle$\displaystyle [0,π]$, trouvez l'aire de la région$\textbf{R}$.

Solution

La région est illustrée dans la figure suivante.

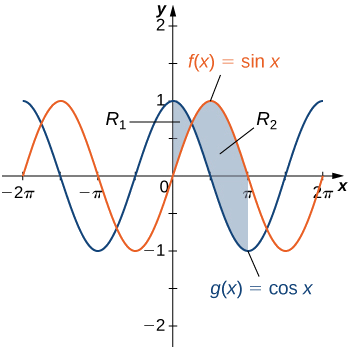
Cette figure comporte deux graphiques. Ce sont les fonctions f (x) = sinx et g (x) = cosx. Ce sont toutes deux des fonctions périodiques qui ressemblent à des ondes. Deux zones ombrées séparent les graphiques. La première zone ombrée est étiquetée « R1 » et comporte g (x) au-dessus de f (x). Cette région commence sur l'axe Y et s'arrête là où les courbes se croisent. La deuxième région est étiquetée « R2 » et commence à l'intersection avec f (x) au-dessus de g (x). La région ombrée s'arrête à x=pi. — Figure$\PageIndex{5}$ : La région située entre deux courbes peut être divisée en deux sous-régions.

Les graphes des fonctions se croisent en$\displaystyle x=π/4$. Pour$\displaystyle x∈[0,π/4], \cos x≥\sin x ,$ ainsi

$\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\cos x−\sin x .$

D'un autre côté, pour$\displaystyle x∈[π/4,π], \sin x ≥\cos x,$ ainsi

$\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\sin x −\cos x.$

Alors

\[ \begin{align*} A =\int ^b_a|f(x)−g(x)|dx \\[4pt] =\int ^π_0|\sin x −\cos x|dx=\int ^{π/4}_0(\cos x−\sin x )dx+\int ^{π}_{π/4}(\sin x −\cos x)dx \\[4pt] =[\sin x +\cos x]|^{π/4}_0+[−\cos x−\sin x ]|^π_{π/4} \\[4pt] =(\sqrt{2}−1)+(1+\sqrt{2})=2\sqrt{2}. \end{align*}\]

La superficie de la région est constituée$\displaystyle 2\sqrt{2}$ d'unités ^₂.

Exercice$\PageIndex{3}$

Si$\textbf{R}$ c'est la région située entre les graphes des fonctions$\displaystyle f(x)=\sin x $ et$\displaystyle g(x)=\cos x$ sur l'intervalle$\displaystyle [π/2,2π]$, trouvez l'aire de la région$\textbf{R}$.

Allusion: Les deux courbes se croisent à$\displaystyle x=(5π)/4.$

Réponse: $\displaystyle 2+2\sqrt{2}$unités ²

Exemple$\PageIndex{4}$: Finding the Area of a Complex Region

Considérez la région illustrée sur la figure$\PageIndex{6}$. Trouvez la zone de$\textbf{R}$.

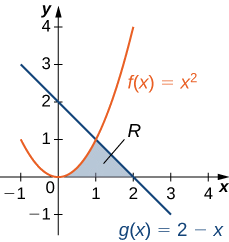
Cette figure comporte deux graphiques dans le premier quadrant. Ce sont les fonctions f (x) = x^2 et g (x) = 2-x. Entre ces graphiques se trouve une zone ombrée, délimitée à gauche par f (x) et à droite par g (x). Tout cela se trouve au-dessus de l'axe X. La région est étiquetée R. La zone ombrée est comprise entre x=0 et x=2. — Figure$\PageIndex{6}$ : Deux intégrales sont nécessaires pour calculer la superficie de cette région.

Solution

Comme pour l'exemple$\PageIndex{3}$, nous devons diviser l'intervalle en deux parties. Les graphes des fonctions se croisent en$\displaystyle x=1$ (définir$\displaystyle f(x)=g(x)$ et résoudre pour x). Nous évaluons donc deux intégrales distinctes : l'une sur l'intervalle$\displaystyle [0,1]$ et l'autre sur l'intervalle$\displaystyle [1,2]$.

Au cours de l'intervalle$\displaystyle [0,1]$, la région est délimitée au-dessus$\displaystyle f(x)=x^2$ et en dessous par l'axe X, donc nous avons

$\displaystyle A_1=\int ^1_0x^2dx=\dfrac{x^3}{3}∣^1_0=\dfrac{1}{3}.$

Au cours de$\displaystyle [1,2],$ l'intervalle, la région est délimitée au-dessus$\displaystyle g(x)=2−x$ et en dessous par l'axe X, donc nous avons

$\displaystyle A_2=\int ^2_1(2−x)dx=[2x−\dfrac{x^2}{2}]∣^2_1=\dfrac{1}{2}.$

En additionnant ces zones, nous obtenons

$\displaystyle A=A_1+A_2=\dfrac{1}{3}+\dfrac{1}{2}=\dfrac{5}{6}.$

La superficie de la région est constituée$\displaystyle 5/6$ d'unités ²^.

Exercice$\PageIndex{4}$

Considérez la région illustrée dans la figure suivante. Trouvez la zone de$\textbf{R}$.

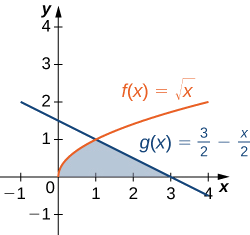
$Cette figure comporte deux graphiques dans le premier quadrant. Ce sont les fonctions f (x) = racine carrée de x et g (x) = 3/2 — x/2. Entre ces graphiques se trouve une zone ombrée, délimitée à gauche par f (x) et à droite par g (x). Tout cela se trouve au-dessus de l'axe X. La zone ombrée est comprise entre x=0 et x=3.$

Allusion: Les deux courbes se croisent en x=1

Réponse: $\displaystyle \dfrac{5}{3}$unités ²

Régions définies par rapport à y

Dans Exemple$\PageIndex{4}$, nous avons dû évaluer deux intégrales distinctes pour calculer la superficie de la région. Cependant, il existe une autre approche qui ne nécessite qu'une seule intégrale. Et si nous traitions les courbes comme des fonctions de$\displaystyle y$, plutôt que comme des fonctions de$\displaystyle x$ ? Réviser la figure. Notez que le graphique de gauche, affiché en rouge, est représenté par la fonction$\displaystyle y=f(x)=x^2$. Nous pourrions tout aussi bien résoudre ce problème pour x et représenter la courbe par la fonction$\displaystyle x=v(y)=\sqrt{y}$. (Notez qu'il$\displaystyle x=−\sqrt{y}$ s'agit également d'une représentation valide de la fonction$\displaystyle y=f(x)=x^2$ en tant que fonction de$\displaystyle y$. Cependant, sur la base du graphique, il est clair que nous sommes intéressés par la racine carrée positive.) De même, le graphe de droite est représenté par la fonction$\displaystyle y=g(x)=2−x$, mais pourrait tout aussi bien être représenté par la fonction$\displaystyle x=u(y)=2−y$. Lorsque les graphes sont représentés en tant que fonctions de$\displaystyle y$, nous voyons que la région est délimitée à gauche par le graphe d'une fonction et à droite par le graphe de l'autre fonction. Par conséquent, si nous intégrons par rapport à$\displaystyle y$, nous devons évaluer une seule intégrale. Développons une formule pour ce type d'intégration.

Les fonctions$\displaystyle u(y)$ Let and$\displaystyle v(y)$ Be sont continues sur un intervalle$\displaystyle [c,d]$ tel que$\displaystyle u(y)≥v(y)$ pour tous$\displaystyle y∈[c,d]$. Nous voulons trouver l'aire entre les graphes des fonctions, comme indiqué sur la figure$\PageIndex{7}$.

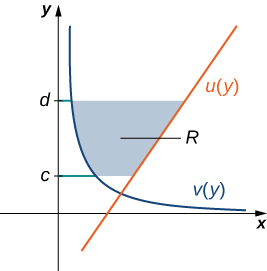
Cette figure comporte deux graphiques dans le premier quadrant. Il s'agit des fonctions v (y) et u (y). Entre ces graphes se trouve une région ombrée, délimitée à gauche par v (y) et à droite par u (y). La région est étiquetée R. La zone ombrée se situe entre les limites horizontales de y=c et y=d. — Figure$\PageIndex{7}$ : Nous pouvons trouver l'aire entre les graphes de deux fonctions,$\displaystyle u(y)$ et$\displaystyle v(y)$.

Cette fois, nous allons partitionner l'intervalle sur l'axe y et utiliser des rectangles horizontaux pour approximer la zone entre les fonctions. Donc, pour$\displaystyle i=0,1,2,…,n$,$\displaystyle Q={y_i}$ soyons une partition régulière de$\displaystyle [c,d]$. Ensuite, pour$\displaystyle i=1,2,…,n$, choisissez un point$\displaystyle y^∗_i∈[y_{i−1},y_i]$, puis, sur chaque intervalle,$\displaystyle [y_{i−1},y_i]$ construisez un rectangle qui s'étend horizontalement de$\displaystyle v(y^0∗_i)$ à$\displaystyle u(y^∗_i)$. La figure$\PageIndex{8a}$ montre les rectangles lorsqu'elle$\displaystyle y^∗_i$ est sélectionnée comme extrémité inférieure de l'intervalle et$\displaystyle n=10$. La figure$\PageIndex{8b}$ montre un rectangle représentatif en détail.

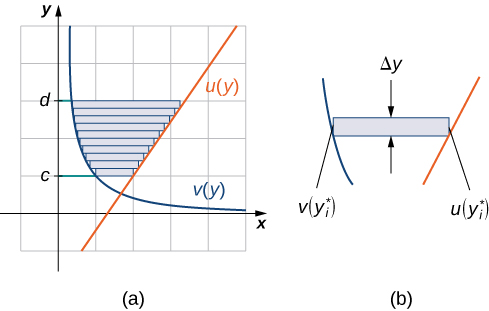
Cette figure comporte trois graphiques. La première figure comporte deux courbes. Il s'agit des fonctions v (y*) et u (y*). Entre ces courbes se trouve un rectangle horizontal. La deuxième figure, intitulée « (a) », est une zone ombrée, délimitée à gauche par v (y) et à droite par u (y). La zone ombrée se situe entre les limites horizontales de y=c et y=d. Cette zone ombrée est divisée en rectangles entre les courbes. La troisième figure, nommée « (b) », représente les deux courbes v (y*) et u (y*). Entre les courbes se trouve un rectangle horizontal de largeur delta y. — Figure$\PageIndex{8}$ : (a) Approximation de l'aire entre les graphes de deux fonctions,$\displaystyle u(y)$ et$\displaystyle v(y)$, avec des rectangles. (b) L'aire d'un rectangle type.

La hauteur de chaque rectangle individuel est$\displaystyle Δy$ et la largeur de chaque rectangle est$\displaystyle u(y^∗_i)−v(y^∗_i)$. Par conséquent, l'aire entre les courbes est d'environ

\[ A≈\sum_{i=1}^n[u(y^∗_i)−v(y^∗_i)]Δy . \nonumber \]

Il s'agit d'une somme de Riemann, donc nous prenons la limite$\displaystyle n→∞,$ comme

\[ \begin{align*} A =\lim_{n→∞}\sum_{i=1}^n[u(y^∗_i)−v(y^∗_i)]Δy \\[4pt] =\int ^d_c[u(y)−v(y)]dy. \end{align*}\]

Ces résultats sont résumés dans le théorème suivant.

Trouver l'aire entre deux courbes, intégrer le long de l'axe Y

Laissez$\displaystyle u(y)$ et$\displaystyle v(y)$ soyez des fonctions continues de telle sorte que$\displaystyle u(y)≥v(y) $ pour tous$\displaystyle y∈[c,d]$. $\textbf{R}$Dénotons la région délimitée à droite par le graphique de$\displaystyle u(y)$, à gauche par le graphique de$\displaystyle v(y)$, et en haut et en bas par les lignes$\displaystyle y=d$ et$\displaystyle y=c$, respectivement. Ensuite, la surface de$\textbf{R}$ est donnée par

\[A=\int ^d_c[u(y)−v(y)]dy. \nonumber \]

Exemple$\PageIndex{5}$: Integrating with Respect to y

Revenons à l'exemple$\PageIndex{4}$, mais cette fois, intégrons en ce qui concerne$\displaystyle y$. $\textbf{R}$Soit la région représentée sur la figure$\PageIndex{9}$. Trouvez la zone de$\textbf{R}$ en intégrant par rapport à$\displaystyle y$.

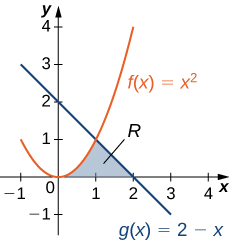
Solution

Nous devons d'abord exprimer les graphes en tant que fonctions de$\displaystyle y$. Comme nous l'avons vu au début de cette section, la courbe de gauche peut être représentée par la fonction$\displaystyle x=v(y)=\sqrt{y}$, et la courbe de droite peut être représentée par la fonction$\displaystyle x=u(y)=2−y$.

Nous devons maintenant déterminer les limites de l'intégration. La région est délimitée en dessous par l'axe X, de sorte que la limite inférieure d'intégration est$\displaystyle y=0$. La limite supérieure de l'intégration est déterminée par le point où les deux graphes se croisent, qui est le point$\displaystyle (1,1)$, de sorte que la limite supérieure de l'intégration est$\displaystyle y=1$. Ainsi, nous l'avons fait$\displaystyle [c,d]=[0,1]$.

En calculant la superficie de la région, nous obtenons

\[ \begin{align*} A =\int ^d_c[u(y)−v(y)]dy \\[4pt] =\int ^1_0[(2−y)−\sqrt{y}]dy\\[4pt] =[2y−\dfrac{y^2}{2}−\dfrac{2}{3}y^{3/2}]∣^1_0\\[4pt] =\dfrac{5}{6}. \end{align*}\]

La superficie de la région est constituée$\displaystyle 5/6$ d'unités ².

Exercice$\PageIndex{5}$

Revoyons le point de contrôle associé à Example$\PageIndex{4}$, mais cette fois, intégrons par rapport à$\displaystyle y$. $\textbf{R}$Soit la région représentée dans la figure suivante. Trouvez la zone de$\textbf{R}$ en intégrant par rapport à$\displaystyle y$.

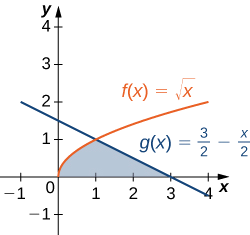
Allusion: Suivez le processus de l'exemple précédent.

Réponse: $\displaystyle \dfrac{5}{3}$unités ²

Concepts clés

Tout comme les intégrales définies peuvent être utilisées pour trouver l'aire sous une courbe, elles peuvent également être utilisées pour trouver l'aire entre deux courbes.
Pour trouver l'aire entre deux courbes définies par des fonctions, intégrez la différence des fonctions.
Si les graphes des fonctions se croisent ou si la région est complexe, utilisez la valeur absolue de la différence des fonctions. Dans ce cas, il peut être nécessaire d'évaluer deux intégrales ou plus et d'ajouter les résultats pour déterminer la superficie de la région.
Parfois, il peut être plus facile de s'intégrer par rapport à y pour trouver la zone. Les principes sont les mêmes quelle que soit la variable utilisée comme variable d'intégration.

Équations clés

Aire située entre deux courbes, intégrée sur l'axe des abscisses

$\displaystyle A=\int ^b_a[f(x)−g(x)]dx$

Aire entre deux courbes, intégrée sur l'axe Y

$\displaystyle A=\int ^d_c[u(y)−v(y)]dy$

Trouver l'aire entre deux courbes

Exemple\(\PageIndex{1}\): Finding the Area of a Region between Two Curves I

Exercice\(\PageIndex{1}\)

Exemple\(\PageIndex{2}\): Finding the Area of a Region between Two Curves II

Exercice\(\PageIndex{2}\)

Déterminer l'aire d'une région entre des courbes qui se croisent

Exemple\(\PageIndex{3}\): Finding the Area of a Region Bounded by Functions That Cross

Exercice\(\PageIndex{3}\)

Exemple\(\PageIndex{4}\): Finding the Area of a Complex Region

Exercice\(\PageIndex{4}\)

Trouver l'aire entre deux courbes, intégrer le long de l'axe Y

Exemple\(\PageIndex{5}\): Integrating with Respect to y

Exercice\(\PageIndex{5}\)