4.7E : Exercices pour la section 4.7

Last updated
Save as PDF

Page ID: 197594

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Pour les exercices 1 à 4, répondez par des preuves, des contre-exemples ou des explications.

1) Lorsque vous trouvez le maximum pour un problème d'optimisation, pourquoi devez-vous vérifier le signe de la dérivée autour des points critiques ?

Réponse: Les points critiques peuvent être les minima, les maxima ou aucun des deux.

2) Pourquoi avez-vous besoin de vérifier les points de terminaison pour détecter les problèmes d'optimisation ?

3) Vrai ou Faux. Pour chaque fonction non linéaire continue, vous pouvez trouver la valeur$x$ qui maximise la fonction.

Réponse: Faux ;$y=−x^2$ n'a qu'un minimum

4) Vrai ou Faux. Pour chaque fonction non constante continue sur un domaine fini fermé, il existe au moins une fonction$x$ qui minimise ou maximise la fonction.

Dans les exercices 5 à 8, configurez et évaluez chaque problème d'optimisation.

5) Pour transporter une valise dans un avion, le$\text{length}+\text{width}+\text{height}$ contenu de la boîte doit être inférieur ou égal$62$ à pouces. En supposant que la hauteur est fixe, montrez que le volume maximum est$V=h\left(31−\frac{1}{2}h\right)^2.$ Quelle hauteur vous permet d'avoir le plus grand volume ?

Réponse: $h=\frac{62}{3}$dans.

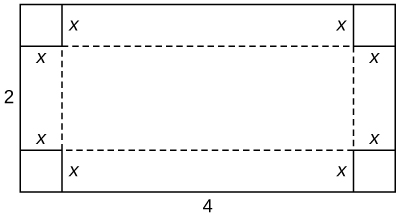
6) Vous construisez une boîte en carton aux dimensions$2$$4$ m par m. Vous découpez ensuite des carrés de taille égale à chaque coin afin de pouvoir plier les bords. Quelles sont les dimensions de la boîte avec le plus grand volume ?

$Un rectangle est dessiné avec une hauteur de 2 et une largeur de 4. Chaque coin comporte un carré sur lequel la longueur de côté x est marquée.$

7) Trouvez l'entier positif qui minimise la somme du nombre et de son inverse.

Réponse: $1$

8) Trouvez deux entiers positifs de telle sorte que leur somme soit$10$, et minimisez et maximisez la somme de leurs carrés.

Dans les exercices 9 à 11, considérez la construction d'un stylo pour délimiter une zone.

9) Vous avez$400\,\text{ft}$ des clôtures pour construire un enclos rectangulaire pour le bétail. Quelles sont les dimensions du stylo qui maximisent la surface ?

Réponse: $100\,\text{ft}$par$100\,\text{ft}$

10) Vous avez$800\,\text{ft}$ des clôtures pour fabriquer un enclos pour les porcs. Si vous avez une rivière sur un côté de votre propriété, quelle est la dimension de l'enclos rectangulaire qui maximise la surface ?

11) Vous devez construire une clôture autour d'une zone de$1600\,\text{ft}^2$. Quelles sont les dimensions du stylo rectangulaire pour minimiser la quantité de matériau nécessaire ?

Réponse: $40\,\text{ft}$par$40\,\text{ft}$

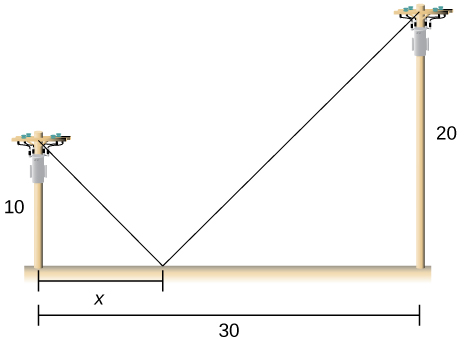
12) Deux pôles sont connectés par un fil qui est également connecté à la terre. Le premier mât est$20\,\text{ft}$ haut et le second mât est$10\,\text{ft}$ haut. Il y a une distance de$30\,\text{ft}$ entre les deux pôles. Où le fil doit-il être ancré au sol pour minimiser la quantité de fil nécessaire ?

$Deux poteaux sont représentés, l'un de 10 de haut et l'autre de 20 de haut. Un triangle droit est formé avec le pôle le plus court dont l'autre côté est long x. La distance entre les deux pôles est de 30.$

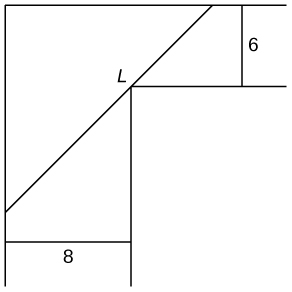
13) [T] Vous emménagez dans un nouvel appartement et remarquez qu'il y a un coin où le couloir se rétrécit de$8\,\text{ft}$ à$6\,\text{ft}$. Quelle est la longueur de l'article le plus long qui peut être transporté horizontalement au coin de la rue ?

$Une figure en L à l'envers est dessinée avec la partie _ de 6 de large et la partie | de 8 de large. Une ligne est tracée entre la partie _ et la partie | qui touche le coin le plus proche de la forme pour former une hypoténuse pour un triangle droit, les autres côtés étant le reste des parties _ et |. Cette ligne est marquée L.$

Réponse: $19.73\,\text{ft}$

14) Le pouls d'un patient est alors mesuré$120 \,\text{bpm}$.$70 \,\text{bpm},\, 80 \,\text{bpm}$ Pour déterminer une mesure précise du pouls, le médecin veut savoir quelle valeur minimise l'expression$(x−70)^2+(x−80)^2+(x−120)^2$ ? Quelle valeur le minimise ?

15) Dans le problème précédent, supposons que le patient était nerveux lors de la troisième mesure, donc nous ne pondérons cette valeur que deux fois moins que les autres. Quelle est la valeur qui minimise$(x−70)^2+ (x−80)^2+\frac{1}{2}(x−120)^2?$

Réponse: $84 \,\text{bpm}$

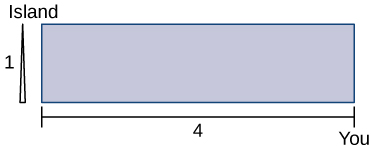
16) Vous pouvez courir à une vitesse de$6$ mi/h et nager à une vitesse de$3$ mi/h et vous êtes situé sur le rivage,$4$ à des kilomètres à l'est d'une île située à un$1$ kilomètre au nord du rivage. Jusqu'où devriez-vous courir vers l'ouest pour minimiser le temps nécessaire pour atteindre l'île ?

$Un rectangle de hauteur 1 et de longueur 4 est dessiné. Dans le coin inférieur droit, il est marqué « Vous » et dans le coin supérieur gauche, il est marqué « Île ».$

Pour les exercices 17 à 19, pensez à un maître-nageur dans une piscine circulaire de diamètre$40$ m. Il doit atteindre une personne qui se noie exactement de l'autre côté de la piscine, en position$C$. Le maître-nageur nage rapidement$v$ et fait le tour de la piscine à toute allure$w=3v.$

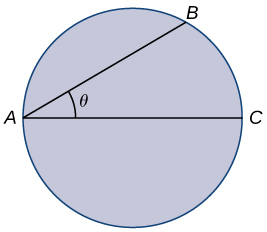
$Un cercle est dessiné avec les points A et C sur un diamètre. Un point B est dessiné sur le cercle de telle sorte que l'angle BAC forme un angle aigu θ.$

17) Trouvez une fonction qui mesure le temps total nécessaire pour atteindre la personne qui se noie en fonction de l'angle de nage,$θ$.

Réponse: $T(θ)=\dfrac{40θ}{3v}+\dfrac{40\cos θ}{v}$

18) Déterminez sous quel angle$θ$ le maître-nageur doit nager pour atteindre la personne qui se noie le plus rapidement possible.

19) Un camion utilise de l'essence sous forme de$g(v)=av+\dfrac{b}{v}$, où$v$ représente la vitesse du camion et$g$ les gallons de carburant par mile. À quelle vitesse la consommation de carburant est-elle minimisée ?

Réponse: $v=\sqrt{\dfrac{b}{a}}$

Pour les exercices 20 à 21, pensez à une limousine qui prend de la$m(v)=\frac{120−2v}{5}\,\text{mi/gal}$ vitesse$v$, le chauffeur coûte cher$$15/\text{h}$ et l'essence$$3.50/\text{gal}$.

20) Trouvez rapidement le coût par mile$v.$

21) Trouvez la vitesse de conduite la moins chère.

Réponse: environ$34.02$ mi/h

Pour les exercices 22 à 24, imaginez une pizzeria qui vend des pizzas pour un chiffre d'affaires$R(x)=ax$ et des coûts$C(x)=b+cx+dx^2$, où$x$ représente le nombre de pizzas.

22) Trouvez la fonction de profit pour le nombre de pizzas. Combien de pizzas génèrent le plus de bénéfices par pizza ?

23) Supposons que$R(x)=10x$ et$C(x)=2x+x^2$. Combien de pizzas vendues maximisent les profits ?

Réponse: La vente de$4$ pizzas maximisera les profits.

24) Supposons que$R(x)=15x$, et$C(x)=60+3x+\frac{1}{2}x^2$. Combien de pizzas vendues maximisent les profits ?

Pour les exercices 25 à 26, considérez un fil de fer$4$ d'un pied de long coupé en deux morceaux. Une pièce forme un cercle avec un rayon$r$ et l'autre forme un carré de côté$x$.

25) Choisissez$x$ de maximiser la somme de leurs superficies.

Réponse: $x = 0$

26) Choisissez$x$ de minimiser la somme de leurs superficies.

Pour les exercices 27 à 30, considérez deux nombres non négatifs$x$ et$y$ tels que$x+y=10$. Maximisez et minimisez les quantités.

(27)$xy$

Réponse: Maximal :$x=5,\,y=5;$
Minimal :$x=0,\,y=10$ et$y=0,\,x=10$

28$x^2y^2$

(29)$y−\dfrac{1}{x}$

Réponse: Maximal :$x=1,\,y=9;$
Minimal : aucun

(30)$x^2−y$

Dans les exercices 31 à 36, dessinez le problème d'optimisation donné et résolvez-le.

31) Déterminez le volume du plus grand cylindre circulaire droit qui s'insère dans une sphère de rayon$1$.

Réponse: $V = \frac{4π}{3\sqrt{3}}$

32) Déterminez le volume du plus grand cône droit qui s'insère dans une sphère de rayon$1$.

33) Trouvez l'aire du plus grand rectangle qui s'insère dans le triangle avec des côtés$x=0,\,y=0$ et$\dfrac{x}{4}+\dfrac{y}{6}=1.$

Réponse: $A = 6$

34) Déterminez le plus grand volume d'un cylindre qui s'insère dans un cône ayant un rayon$R$ et une hauteur de base$h$.

35) Déterminez les dimensions du volume du cylindre fermé$V=16π$ dont la surface est la plus faible.

Réponse: $r=2,\,h=4$

36) Déterminez les dimensions d'un cône droit dont la surface$S=4π$ possède le plus grand volume.

Pour les exercices 37 à 40, considérez les points sur les graphes des équations données. Utilisez une calculatrice pour représenter graphiquement les fonctions.

37) [T] Où se trouve la ligne la$y=5−2x$ plus proche de l'origine ?

Réponse: $(2,1)$

38) [T] Où se trouve la ligne la$y=5−2x$ plus proche du point$(1,1)$ ?

39) [T] Où se trouve la parabole la$y=x^2$ plus proche du point$(2,0)$ ?

Réponse: $(0.8351,0.6974)$

40) [T] Où se trouve la parabole la$y=x^2$ plus proche du point$(0,3)$ ?

Dans les exercices 41 à 45, configurez, mais n'évaluez pas, chaque problème d'optimisation.

41) Une fenêtre est composée d'un demi-cercle placé au-dessus d'un rectangle. Si vous avez$20\,\text{ft}$ des matériaux de charpente pour le cadre extérieur, quelle est la taille maximale de la fenêtre que vous pouvez créer ? Utilisez r pour représenter le rayon du demi-cercle.

$Une fenêtre semi-circulaire est dessinée avec un rayon r.$

Réponse: $A=20r−2r^2−\frac{1}{2}πr^2$

42) Vous avez une rangée de plants de$20$ pastèques qui produisent en moyenne$30$ des pastèques chacun. Pour toute plante de pastèque supplémentaire plantée, la production par plant de pastèque diminue d'une pastèque. Combien de plants de pastèque supplémentaires devriez-vous planter ?

43) Vous construisez une boîte pour que votre chat puisse dormir. Le matériau en peluche pour le fond carré de la boîte coûte$$5/\text{ft}^2$ et le matériau pour les côtés coûte$$2/\text{ft}^2$. Vous avez besoin d'une boîte avec du volume$4\,\text{ft}^3$. Trouvez les dimensions de la boîte qui minimisent les coûts. $x$Sert à représenter la longueur du côté de la boîte.

Réponse: $C(x)=5x^2+\dfrac{32}{x}$

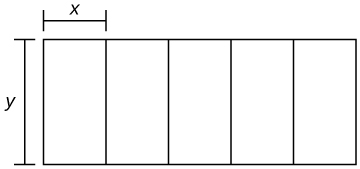
44) Vous construisez cinq enclos identiques adjacents les uns aux autres d'une superficie totale de$1000\,\text{m}^2$, comme le montre la figure suivante. Quelles dimensions devez-vous utiliser pour minimiser la quantité de clôtures ?

$Un rectangle est divisé en cinq sections, et chaque section a une longueur y et une largeur x.$

45) Vous êtes le gérant d'un complexe d'appartements avec des$50$ unités. Lorsque vous fixez le loyer à$$800/\text{month}$, tous les appartements sont loués. Au fur et à mesure que vous augmentez le loyer$$25/\text{month}$, un appartement de moins est loué. Les coûts de maintenance sont$$50/\text{month}$ encourus pour chaque unité occupée. Quel est le loyer qui maximise le montant total des bénéfices ?

Réponse: $P(x)=(50−x)(800+25x−50)$