4.6E : Exercices pour la section 4.6

Last updated
Save as PDF

Page ID: 197712

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Pour les exercices 1 à 5, examinez les graphiques. Déterminez où se situent les asymptotes verticales.

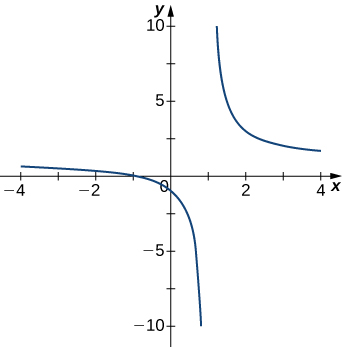
$La fonction représentée sur le graphique diminue très rapidement à mesure qu'elle s'approche de x = 1 depuis la gauche, et de l'autre côté de x = 1, elle semble commencer près de l'infini puis diminuer rapidement.$

Réponse: $x=1$

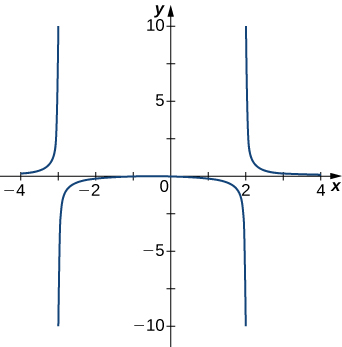
$La fonction représentée sur le graphique augmente très rapidement à mesure qu'elle s'approche de x = −3 depuis la gauche, et de l'autre côté de x = −3, elle semble commencer près de l'infini négatif, puis augmenter rapidement pour former une sorte de forme de U pointant vers le bas, l'autre côté du U étant à x = 2. De l'autre côté de x = 2, le graphique semble commencer près de l'infini puis diminuer rapidement.$

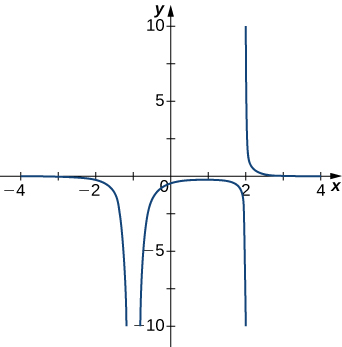
$La fonction représentée sur le graphique diminue très rapidement à mesure qu'elle s'approche de x = −1 depuis la gauche, et de l'autre côté de x = −1, elle semble commencer près de l'infini négatif puis augmenter rapidement pour former une sorte de forme de U pointant vers le bas, l'autre côté du U étant à x = 2. De l'autre côté de x = 2, le graphique semble commencer près de l'infini puis diminuer rapidement.$

Réponse: $x=−1,\;x=2$

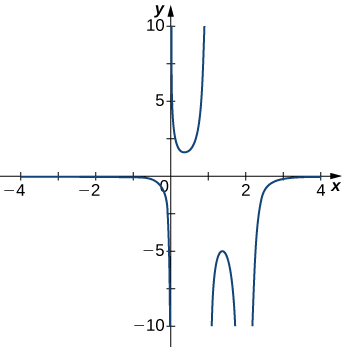
$La fonction représentée sur le graphique diminue très rapidement à mesure qu'elle s'approche de x = 0 depuis la gauche, et de l'autre côté de x = 0, elle semble commencer près de l'infini puis diminuer rapidement pour former une sorte de forme de U pointant vers le haut, l'autre côté du U étant à x = 1. De l'autre côté de x = 1, il y a une autre forme de U pointant vers le bas, son autre côté étant à x = 2. De l'autre côté de x = 2, le graphique semble commencer près de l'infini négatif, puis augmenter rapidement.$

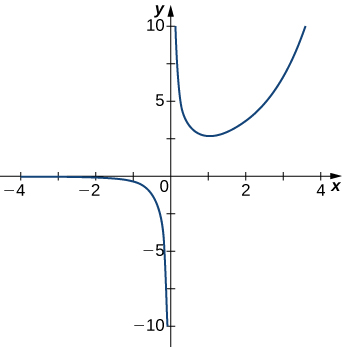
$La fonction représentée sur le graphique diminue très rapidement à mesure qu'elle s'approche de x = 0 depuis la gauche, et de l'autre côté de x = 0, elle semble commencer près de l'infini puis diminuer rapidement pour former une sorte de forme en U pointant vers le haut, l'autre côté étant une fonction normale qui apparaît comme si elle prendrait la totalité de valeurs de l'axe X.$

Réponse: $x=0$

Pour les fonctions des exercices 6$f(x)$ à 10, déterminez s'il existe une asymptote à$x=a$. Justifiez votre réponse sans utiliser de graphique sur une calculatrice.

6)$f(x)=\dfrac{x+1}{x^2+5x+4},\quad a=−1$

7)$f(x)=\dfrac{x}{x−2},\quad a=2$

Réponse: Oui, il existe une asymptote verticale à$x = 2$.

8)$f(x)=(x+2)^{3/2},\quad a=−2$

9)$f(x)=(x−1)^{−1/3},\quad a=1$

Réponse: Oui, il existe une asymptote verticale à$x = 1$.

10)$f(x)=1+x^{−2/5},\quad a=1$

Dans les exercices 11 à 20, évaluez la limite.

11)$\displaystyle \lim_{x→∞}\frac{1}{3x+6}$

Réponse: $\displaystyle \lim_{x→∞}\frac{1}{3x+6} = 0$

(12)$\displaystyle \lim_{x→∞}\frac{2x−5}{4x}$

13)$\displaystyle \lim_{x→∞}\frac{x^2−2x+5}{x+2}$

Réponse: $\displaystyle \lim_{x→∞}\frac{x^2−2x+5}{x+2} = ∞$

(14)$\displaystyle \lim_{x→−∞}\frac{3x^3−2x}{x^2+2x+8}$

15)$\displaystyle \lim_{x→−∞}\frac{x^4−4x^3+1}{2−2x^2−7x^4}$

Réponse: $\displaystyle \lim_{x→−∞}\frac{x^4−4x^3+1}{2−2x^2−7x^4} = −\frac{1}{7}$

16)$\displaystyle \lim_{x→∞}\frac{3x}{\sqrt{x^2+1}}$

17)$\displaystyle \lim_{x→−∞}\frac{\sqrt{4x^2−1}}{x+2}$

Réponse: $\displaystyle \lim_{x→−∞}\frac{\sqrt{4x^2−1}}{x+2} = -2$

18)$\displaystyle \lim_{x→∞}\frac{4x}{\sqrt{x^2−1}}$

19)$\displaystyle \lim_{x→−∞}\frac{4x}{\sqrt{x^2−1}}$

Réponse: $\displaystyle \lim_{x→−∞}\frac{4x}{\sqrt{x^2−1}} = -4$

(20)$\displaystyle \lim_{x→∞}\frac{2\sqrt{x}}{x−\sqrt{x}+1}$

Pour les exercices 21 à 25, trouvez les asymptotes horizontales et verticales.

(21)$f(x)=x−\dfrac{9}{x}$

Réponse: Horizontal : aucun,
vertical :$x=0$

22)$f(x)=\dfrac{1}{1−x^2}$

23)$f(x)=\dfrac{x^3}{4−x^2}$

Réponse: Horizontal : aucun,
vertical :$x=±2$

(24)$f(x)=\dfrac{x^2+3}{x^2+1}$

25)$f(x)=\sin(x)\sin(2x)$

Réponse: Horizontal : aucun,
vertical : aucun

26)$f(x)=\cos x+\cos(3x)+\cos(5x)$

(27)$f(x)=\dfrac{x\sin(x)}{x^2−1}$

Réponse: Horizontal :$y=0,$
Vertical :$x=±1$

28)$f(x)=\dfrac{x}{\sin(x)}$

(29)$f(x)=\dfrac{1}{x^3+x^2}$

Réponse: Horizontal :$y=0,$
Vertical :$x=0$ et$x=−1$

(30)$f(x)=\dfrac{1}{x−1}−2x$

31)$f(x)=\dfrac{x^3+1}{x^3−1}$

Réponse: Horizontal :$y=1,$
Vertical :$x=1$

32)$f(x)=\dfrac{\sin x+\cos x}{\sin x−\cos x}$

33)$f(x)=x−\sin x$

Réponse: Horizontal : aucun,
vertical : aucun

34)$f(x)=\dfrac{1}{x}−\sqrt{x}$

Pour les exercices 35 à 38, construisez une fonction$f(x)$ qui possède les asymptotes donnés.

35)$x=1$ et$y=2$

Réponse: Les réponses peuvent varier, par exemple :$y=\dfrac{2x}{x−1}$

36)$x=1$ et$y=0$

(37)$y=4, \;x=−1$

Réponse: Les réponses peuvent varier, par exemple :$y=\dfrac{4x}{x+1}$

38)$x=0$

Dans les exercices 39 à 43, tracez la fonction sur une calculatrice graphique sur la fenêtre$x=[−5,5]$ et estimez l'asymptote ou la limite horizontale. Calculez ensuite l'asymptote ou la limite horizontale réelle.

39) [T]$f(x)=\dfrac{1}{x+10}$

Réponse: $\displaystyle \lim_{x→∞}\frac{1}{x+10}=0$$f$a donc une asymptote horizontale de$y=0$.

40) [T]$f(x)=\dfrac{x+1}{x^2+7x+6}$

41) [T]$\displaystyle \lim_{x→−∞}x^2+10x+25$

Réponse: $\displaystyle \lim_{x→−∞}x^2+10x+25 = ∞$

42) [T]$\displaystyle \lim_{x→−∞}\frac{x+2}{x^2+7x+6}$

43) [T]$\displaystyle \lim_{x→∞}\frac{3x+2}{x+5}$

Réponse: $\displaystyle \lim_{x→∞}\frac{3x+2}{x+5}=3$cette fonction a donc une asymptote horizontale de$y=3$.

Dans les exercices 44 à 55, dessinez un graphique des fonctions sans utiliser de calculatrice. Assurez-vous de noter toutes les caractéristiques importantes du graphique : maxima et minima locaux, points d'inflexion et comportement asymptotique.

44)$y=3x^2+2x+4$

45)$y=x^3−3x^2+4$

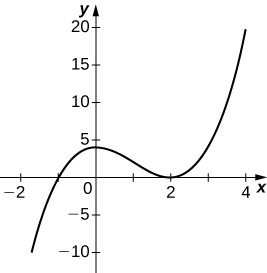
Réponse: $La fonction commence dans le troisième quadrant, augmente pour passer (−1, 0), augmente jusqu'à un maximum et y intercepte à 4, diminue pour toucher (2, 0), puis augmente jusqu'à (4, 20).$

46)$y=\dfrac{2x+1}{x^2+6x+5}$

47)$y=\dfrac{x^3+4x^2+3x}{3x+9}$

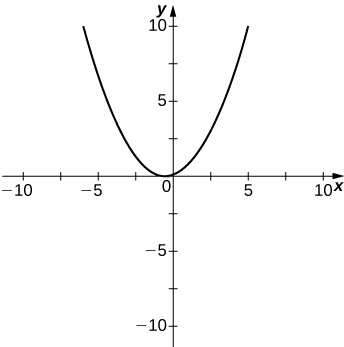
Réponse: $Parabole orientée vers le haut avec un minimum compris entre x = 0 et x = −1 avec une intersection y comprise entre 0 et 1.$

48)$y=\dfrac{x^2+x−2}{x^2−3x−4}$

49)$y=\sqrt{x^2−5x+4}$

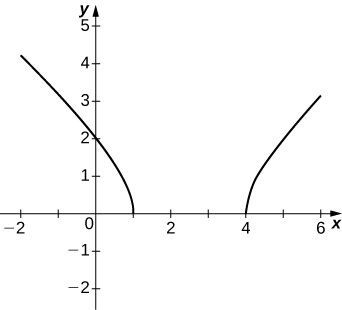
Réponse: $Ce graphe commence à (−2, 4) et diminue de façon convexe jusqu'à (1, 0). Ensuite, le graphique recommence à (4, 0) et augmente de manière convexe jusqu'à (6, 3).$

50)$y=2x\sqrt{16−x^2}$

51)$y=\dfrac{\cos x}{x}$, sur$x=[−2π,2π]$

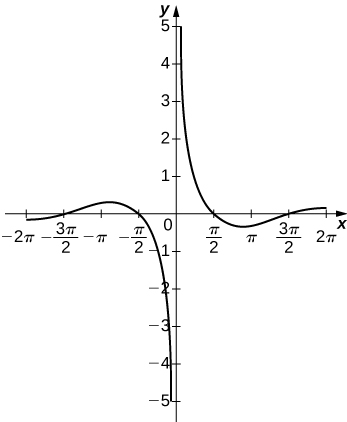
Réponse: $Ce graphique présente une asymptote verticale à x = 0. La première partie de la fonction apparaît dans les deuxième et troisième quadrants et commence dans le troisième quadrant juste en dessous (−2π, 0), augmente et passe par l'axe x à −3π/2, atteint un maximum puis diminue par l'axe x à −π/2 avant de s'approcher de l'asymptote. De l'autre côté de l'asymptote, la fonction commence dans le premier quadrant, diminue rapidement pour passer par π/2, diminue jusqu'à un minimum local puis augmente jusqu'à (3π/2, 0) avant de rester juste au-dessus (2π, 0).$

52)$y=e^x−x^3$

53)$y=x\tan x, \quad x=[−π,π]$

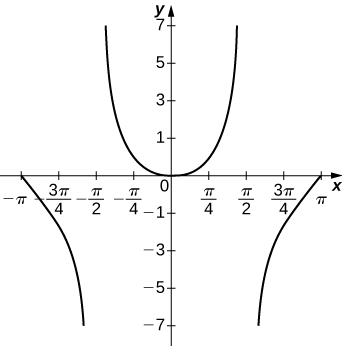
Réponse: $Ce graphique présente des asymptotes verticales à x = ±π/2. Le graphique est symétrique par rapport à l'axe y, il suffira donc de décrire le côté gauche. La fonction commence à (−π, 0) et diminue rapidement jusqu'à l'asymptote. Elle commence ensuite de l'autre côté de l'asymptote dans le deuxième quadrant et diminue jusqu'à l'origine.$

(54)$y=x\ln(x), \quad x>0$

55)$y=x^2\sin(x),\quad x=[−2π,2π]$

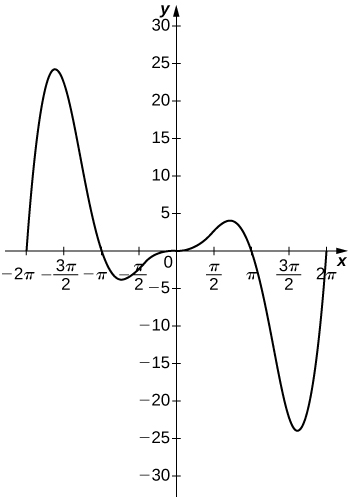
Réponse: $Cette fonction commence à (−2π, 0), augmente jusqu'à environ (−3π/2, 25), diminue jusqu'à (−π, 0), atteint un minimum local puis augmente jusqu'à l'origine. De l'autre côté de l'origine, le graphique est identique mais inversé, c'est-à-dire qu'il est congruent à l'autre moitié par une rotation de 180 degrés.$

56) Car$f(x)=\dfrac{P(x)}{Q(x)}$ pour avoir une asymptote$y=2$ alors aux polynômes$P(x)$ et$Q(x)$ doit avoir quelle relation ?

57) Car$f(x)=\dfrac{P(x)}{Q(x)}$ pour avoir une asymptote at$x=0$, alors les polynômes$P(x)$ et$Q(x).$ doit avoir quelle relation ?

Réponse: $Q(x).$doit avoir$x^{k+1}$ comme facteur, où$P(x)$ a$x^k$ comme facteur.

58) Si$f′(x)$ a des asymptotes à$y=3$ et$x=1$, alors$f(x)$ quelles asymptotes ?

59) Les deux$f(x)=\dfrac{1}{x−1}$$g(x)=\dfrac{1}{(x−1)^2}$ ont des asymptotes$x=1$ et$y=0.$ quelle est la différence la plus évidente entre ces deux fonctions ?

Réponse: $\displaystyle \lim_{x→1^−}f(x)=-\infty \text{ and } \lim_{x→1^−}g(x)=\infty$

60) Vrai ou faux : chaque ratio de polynômes possède des asymptotes verticales.