5.6 : L'effet Doppler
- Page ID
- 192003
Objectifs d'apprentissage
À la fin de cette section, vous serez en mesure de :
- Expliquez pourquoi les raies spectrales de photons que nous observons à partir d'un objet changent en raison du mouvement de l'objet vers nous ou s'éloigne de nous
- Décrire comment utiliser l'effet Doppler pour déduire comment les objets astronomiques se déplacent dans l'espace
Les deux dernières sections vous ont fait découvrir de nombreux nouveaux concepts, et nous espérons qu'à travers ceux-ci, vous avez vu émerger une idée majeure. Les astronomes peuvent en apprendre davantage sur les éléments des étoiles et des galaxies en décodant les informations contenues dans leurs raies spectrales. Il y a cependant un facteur qui complique l'apprentissage de la façon de décoder le message de la lumière des étoiles. Si une étoile se déplace vers nous ou s'éloigne de nous, ses raies se trouveront à un endroit légèrement différent de celui où elles se trouveraient dans une étoile au repos. Et la plupart des objets de l'univers ont un certain mouvement par rapport au Soleil.
Le mouvement affecte les vagues
En 1842, Christian Doppler a d'abord mesuré l'effet du mouvement sur les vagues en engageant un groupe de musiciens pour jouer sur un wagon ouvert alors qu'il se déplaçait le long de la voie ferrée. Il a ensuite appliqué ce qu'il a appris à toutes les ondes, y compris la lumière, et a souligné que si une source lumineuse s'approche ou s'éloigne de l'observateur, les ondes lumineuses seront, respectivement, plus rapprochées ou dispersées. Le principe général, désormais connu sous le nom d'effet Doppler, est illustré sur la figure\(\PageIndex{1}\).
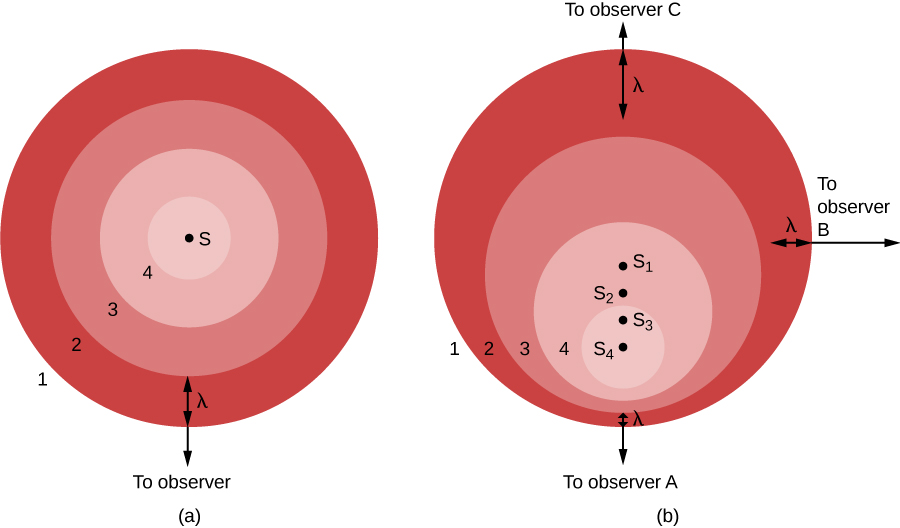
Sur la figure\(\PageIndex{1a}\), la source lumineuse (S) est au repos par rapport à l'observateur. La source émet une série de vagues dont nous avons étiqueté les crêtes 1, 2, 3 et 4. Les ondes lumineuses se répandent uniformément dans toutes les directions, comme les ondulations d'une éclaboussure dans un étang. Les crêtes sont séparées par une distance, λ, où λ est la longueur d'onde. L'observateur, qui se trouve dans la direction du bas de l'image, voit les ondes lumineuses se déplacer bien et uniformément, à une longueur d'onde l'une de l'autre. Les observateurs situés n'importe où ailleurs verraient la même chose.
En revanche, si la source de lumière se déplace par rapport à l'observateur, comme le montre la figure\(\PageIndex{1b}\), la situation est plus compliquée. Entre le moment où une crête est émise et la suivante prête à sortir, la source s'est légèrement déplacée, vers le bas de la page. Du point de vue de l'observateur A, ce mouvement de la source a réduit la distance entre les crêtes : il comprime les crêtes, pourrait dire cet observateur.
Dans la figure\(\PageIndex{1b}\), nous montrons la situation du point de vue de trois observateurs. La source est vue dans quatre positions,\(S_1\),\(S_2\), et\(S_3\)\(S_4\), chacune correspondant à l'émission d'une crête d'onde. Pour l'observateur A, les ondes semblent se suivre de plus près, à une longueur d'onde diminuée et donc à une fréquence accrue. (N'oubliez pas que toutes les ondes lumineuses se déplacent à la vitesse de la lumière dans l'espace vide, quoi qu'il arrive. Cela signifie que le mouvement ne peut pas affecter la vitesse, mais uniquement la longueur d'onde et la fréquence. Lorsque la longueur d'onde diminue, la fréquence doit augmenter. Si les vagues sont plus courtes, un plus grand nombre de vagues pourront passer pendant chaque seconde.)
La situation n'est pas la même pour les autres observateurs. Regardons la situation du point de vue de l'observateur C, situé en face de l'observateur A sur la figure\(\PageIndex{1}\). Pour elle, la source s'éloigne de sa position. Par conséquent, les ondes ne sont pas comprimées mais dispersées par le mouvement de la source. Les crêtes arrivent avec une longueur d'onde accrue et une fréquence diminuée. Pour l'observateur B, dans une direction perpendiculaire au mouvement de la source, aucun effet n'est observé. La longueur d'onde et la fréquence restent les mêmes que dans la partie (a) de la figure.
Nous pouvons voir sur cette illustration que l'effet Doppler est produit uniquement par un mouvement vers ou loin de l'observateur, un mouvement appelé vitesse radiale. Un mouvement latéral ne produit pas un tel effet. Les observateurs situés entre A et B observeraient un certain raccourcissement des ondes lumineuses pour la partie du mouvement de la source située le long de leur ligne de visée. Les observateurs situés entre B et C observeraient un allongement des ondes lumineuses situées le long de leur ligne de visée.
Vous avez peut-être entendu l'effet Doppler avec des ondes sonores. Lorsqu'un sifflet de train ou une sirène de police s'approche de vous puis s'éloigne, vous remarquerez une diminution de la tonalité (c'est-à-dire la façon dont les sens humains interprètent la fréquence des ondes sonores) des ondes sonores. Par rapport aux vagues au repos, elles sont passées d'un peu plus fréquentes lorsqu'elles s'approchent de vous à un peu moins fréquentes lorsqu'elles s'éloignent de vous.
Un bel exemple de ce changement dans le son d'un sifflet de train peut être entendu à la fin de la chanson classique des Beach Boys « Caroline, No » sur leur album Pet Sounds. Pour entendre ce son, rendez-vous sur cette version YouTube de la chanson. Le bruit du train commence vers 2 h 20.
Changements de couleur
Lorsque la source des ondes se déplace vers vous, la longueur d'onde diminue légèrement. Si les ondes impliquées sont de la lumière visible, les couleurs de la lumière changent légèrement. À mesure que la longueur d'onde diminue, elles se déplacent vers l'extrémité bleue du spectre : les astronomes appellent cela un décalage vers le bleu (puisque l'extrémité du spectre est réellement violette, le terme devrait probablement être violet, mais le bleu est une couleur plus courante). Lorsque la source s'éloigne de vous et que la longueur d'onde s'allonge, nous appelons le changement de couleur un décalage vers le rouge. Comme l'effet Doppler a été utilisé pour la première fois avec la lumière visible en astronomie, les termes « décalage vers le bleu » et « décalage vers le rouge » sont devenus bien établis. Aujourd'hui, les astronomes utilisent ces mots pour décrire les variations des longueurs d'onde des ondes radio ou des rayons X aussi confortablement qu'ils les utilisent pour décrire les modifications de la lumière visible.
Plus le mouvement vers nous ou s'éloigne de nous, plus le décalage Doppler est important. Si le mouvement relatif se situe entièrement le long de la ligne de visée, la formule du décalage Doppler de la lumière est
\[\dfrac{\Delta λ}{λ}= \frac{v}{c} \nonumber\]
où\(\lambda\) est la longueur d'onde émise par la source,\(\Delta \lambda\) est la différence entre\(\lambda\) et la longueur d'onde mesurée par l'observateur,\(c\) est la vitesse de la lumière et\(v\) est la vitesse relative de l'observateur et de la source dans la ligne de visée. La variable\(v\) est comptée comme positive si la vitesse est celle d'une récession, et négative si elle est une vitesse d'approche. En résolvant cette équation pour la vitesse, nous trouvons
\[ v = c \times \dfrac{\Delta \lambda}{\lambda}. \nonumber\]
Si une étoile s'approche de nous ou s'éloigne de nous, les longueurs d'onde de la lumière dans son spectre continu apparaissent respectivement raccourcies ou allongées, tout comme celles des lignes sombres. Cependant, à moins que sa vitesse ne soit de dizaines de milliers de kilomètres par seconde, l'étoile n'apparaît pas nettement plus bleue ou plus rouge que la normale. Le décalage Doppler n'est donc pas facilement détecté dans un spectre continu et ne peut pas être mesuré avec précision dans un tel spectre. Les longueurs d'onde des raies d'absorption peuvent toutefois être mesurées avec précision et leur décalage Doppler est relativement simple à détecter.
Exemple\(\PageIndex{1}\) : L'effet Doppler
Nous pouvons utiliser l'équation de l'effet Doppler pour calculer la vitesse radiale d'un objet si nous connaissons trois choses : la vitesse de la lumière, la longueur d'onde originale (non décalée) de la lumière émise et la différence entre la longueur d'onde de la lumière émise et la longueur d'onde que nous observons. Pour des raies d'absorption ou d'émission particulières, nous connaissons généralement exactement la longueur d'onde de la raie dans nos laboratoires sur Terre, là où la source de lumière ne bouge pas. Nous pouvons mesurer la nouvelle longueur d'onde avec nos instruments installés au télescope, et ainsi connaître la différence de longueur d'onde due au décalage Doppler. La vitesse de la lumière étant une constante universelle, on peut alors calculer la vitesse radiale de l'étoile.
Une raie d'émission particulière d'hydrogène est initialement émise à une longueur d'onde de 656,3 nm à partir d'un nuage de gaz. À notre télescope, nous observons que la longueur d'onde de la raie d'émission est de 656,6 nm. À quelle vitesse ce nuage de gaz se déplace-t-il vers ou loin de la Terre ?
Solution
Comme la lumière est déplacée vers une longueur d'onde plus longue (décalée vers le rouge), nous savons que ce nuage de gaz s'éloigne de nous. La vitesse peut être calculée à l'aide de la formule de décalage Doppler :
\[ν=c×\dfrac{\Delta \lambda}{\lambda}= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left( \dfrac{0.3 ~ \text{nm}}{656.3 ~ \text{nm}} \right)= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.3 \times 10^{–9} ~ \text{m}}{656.3 \times 10^{–9} ~ \text{m}} \right)=140,000 ~ \text{m/s} =140 ~ \text{km/s} \nonumber\]
Exercice\(\PageIndex{1}\)
Supposons qu'une raie spectrale d'hydrogène, normalement à 500 nm, soit observée dans le spectre d'une étoile comme étant à 500,1 nm. À quelle vitesse l'étoile se déplace-t-elle vers ou s'éloigne-t-elle de la Terre ?
- Réponse
-
Parce que la lumière est déplacée vers une longueur d'onde plus longue, l'étoile s'éloigne de nous :
\[ν=c \times \dfrac{\Delta \lambda}{\lambda}= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.1 ~ \text{nm}}{500 ~ \text{nm}} \right)=\left( 3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.1 \times 10^{–9} ~ \text{m}}{500 \times 10^{–9} ~ \text{m}} \right)=60,000 ~ \text{m/s}\]
Sa vitesse est de 60 000 m/s.
Vous vous demandez peut-être maintenant : si toutes les étoiles se déplacent et que le mouvement modifie la longueur d'onde de chaque raie spectrale, ne serait-ce pas un désastre pour les astronomes qui essaient de déterminer quels éléments sont présents dans les étoiles ? Après tout, c'est la longueur d'onde (ou couleur) précise qui indique aux astronomes quelles raies appartiennent à quel élément. Et nous mesurons d'abord ces longueurs d'onde dans des récipients de gaz de nos laboratoires, qui ne bougent pas. Si chaque raie du spectre d'une étoile est maintenant déplacée par son mouvement vers une longueur d'onde (couleur) différente, comment pouvons-nous être sûrs des raies et des éléments que nous observons dans une étoile dont nous ne connaissons pas la vitesse ?
Prends courage. Cette situation semble pire qu'elle ne l'est en réalité. Les astronomes jugent rarement la présence d'un élément dans un objet astronomique à l'aide d'une seule ligne. C'est le motif des raies propres à l'hydrogène ou au calcium qui nous permet de déterminer si ces éléments font partie de l'étoile ou de la galaxie que nous observons. L'effet Doppler ne modifie pas le motif des lignes d'un élément donné ; il déplace simplement l'ensemble du motif légèrement vers des longueurs d'onde plus rouges ou plus bleues. Le motif décalé est encore assez facile à reconnaître. Mieux encore, lorsque nous reconnaissons le schéma d'un élément familier, nous obtenons un avantage : le décalage du motif peut nous permettre de déterminer la vitesse des objets dans notre ligne de visée.
La formation des astronomes comprend de nombreux travaux sur l'apprentissage du décodage de la lumière (et d'autres rayonnements électromagnétiques). Un « décodeur » habile peut connaître la température d'une étoile, les éléments qu'elle contient et même sa vitesse dans une direction vers nous ou loin de nous. C'est vraiment une quantité impressionnante d'informations pour les étoiles situées à des années-lumière.
Résumé
Si un atome se déplace vers nous lorsqu'un électron change d'orbite et produit une raie spectrale, nous voyons cette raie légèrement décalée vers le bleu de sa longueur d'onde normale dans un spectre. Si l'atome s'éloigne, nous voyons la ligne se déplacer vers le rouge. Ce décalage est connu sous le nom d'effet Doppler et peut être utilisé pour mesurer les vitesses radiales d'objets distants.
Lexique
- Effet Doppler
- le changement apparent de longueur d'onde ou de fréquence du rayonnement provenant d'une source en raison de son mouvement relatif en direction ou en direction de l'observateur
- vitesse radiale
- mouvement vers ou loin de l'observateur ; composante de la vitesse relative qui se trouve dans la ligne de visée


