13.7 : Probabilité
- Page ID
- 194972
- Construisez des modèles de probabilité.
- Calculez les probabilités de résultats tout aussi probables.
- Calculez les probabilités de l'union de deux événements.
- Utilisez la règle du complément pour trouver des probabilités.
- Calculez les probabilités en utilisant la théorie
Les habitants du sud-est des États-Unis ne connaissent que trop bien les cartes, connues sous le nom de modèles spaghettis, comme celle de Figure\(\PageIndex{1}\). Ils combinent un ensemble de données météorologiques pour prédire la trajectoire la plus probable d'un ouragan. Chaque ligne colorée représente un chemin possible. Le groupe de lignes ondulées peut commencer à ressembler à des brins de spaghettis, d'où son nom. Dans cette section, nous étudierons les méthodes permettant de faire ce type de prédictions.
Figure\(\PageIndex{1}\) : Exemple de « modèle spaghetti », qui peut être utilisé pour prédire les trajectoires possibles d'une tempête tropicale. 1
Construction de modèles de probabilité
Supposons que nous roulions un cube numérique à six côtés. Lancer un cube numérique est un exemple d'expérience ou d'activité dont le résultat est observable. Les nombres sur le cube sont les résultats possibles, ou les résultats, de cette expérience. L'ensemble de tous les résultats possibles d'une expérience est appelé espace d'échantillonnage de l'expérience. L'espace d'échantillonnage pour cette expérience est\(\{1,2,3,4,5,6 \}\). Un événement est un sous-ensemble quelconque d'un espace d'échantillonnage.
La probabilité d'un événement est connue sous le nom de probabilité. La probabilité d'un événement pp est un nombre qui satisfait toujours\(0≤p≤1\), où\(0\) indique un événement impossible et\(1\) indique un certain événement. Un modèle de probabilité est une description mathématique d'une expérience répertoriant tous les résultats possibles et leurs probabilités associées. Par exemple, s'il y a une\(1\%\) chance de gagner une tombola et une\(99\%\) chance de perdre la tombola, un modèle de probabilité ressemblerait beaucoup à Tableau\(\PageIndex{1}\).
| Résultat | Probabilité |
|---|---|
| Gagner au tirage au sort | 1 % |
| Perdre la tombola | 99 % |
La somme des probabilités répertoriées dans un modèle de probabilité doit être égale à\(1\), ou\(100\%\).
- Identifiez chaque résultat.
- Déterminez le nombre total de résultats possibles.
- Comparez chaque résultat au nombre total de résultats possibles.
Construisez un modèle de probabilité pour lancer un seul dé juste, l'événement étant le nombre indiqué sur le dé.
Solution
Commencez par dresser une liste de tous les résultats possibles de l'expérience. Les résultats possibles sont les nombres qui peuvent être lancés :\(1\)\(2\),\(3\),\(4\),\(5\), et\(6\). Six résultats possibles constituent l'espace d'échantillonnage.
Attribuez des probabilités à chaque résultat dans l'espace d'échantillonnage en déterminant un rapport entre le résultat et le nombre de résultats possibles. Il y a un de chacun des six nombres sur le cube, et il n'y a aucune raison de penser qu'un visage en particulier est plus susceptible d'apparaître que n'importe quel autre, donc la probabilité de lancer un nombre est\(16\).
| Résultat | Rouleau de 1 | Rouleau de 2 | Rouleau de 3 | Rouleau de 4 | Rouleau de 5 | Rouleau de 6 |
|---|---|---|---|---|---|---|
| Probabilité | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) | \(\dfrac{1}{6}\) |
Non. Les probabilités peuvent être exprimées sous forme de fractions, de décimales ou de pourcentages. La probabilité doit toujours être un nombre compris entre\(0\) et\(1\), inclus\(0\) et\(1\).
Calculer les probabilités de résultats tout aussi probables
\(S\)Soyons un espace d'échantillonnage pour une expérience. Lors de l'étude des probabilités, un événement est un sous-ensemble de\(S\). Lorsque les résultats d'une expérience sont tous également probables, nous pouvons déterminer la probabilité d'un événement en divisant le nombre de résultats de l'événement par le nombre total de résultats dans\(S\). Supposons qu'un cube numérique soit lancé et que nous souhaitions déterminer la probabilité que l'événement « lance un nombre inférieur ou égal à 4 ». Il y a 4 résultats possibles dans l'événement et 6 résultats possibles dans\(S\), donc la probabilité de l'événement est de\(\dfrac{4}{6}=\dfrac{2}{3}\).
La probabilité d'un événement\(E\) dans une expérience avec un espace d'échantillonnage\(S\) avec des résultats tout aussi probables est donnée par
\[P(E)=\dfrac{\text{number of elements in }E}{\text{number of elements in }S}=\dfrac{n(E)}{n(S)}\]
\(E\)est un sous-ensemble de\(S\), il est donc toujours vrai que\(0≤P(E)≤1\).
Un cube numérique est lancé. Détermine la probabilité de lancer un nombre impair.
Solution
L'événement « lancer un nombre impair » contient trois résultats. Il existe des résultats\(6\) tout aussi probables dans l'espace d'échantillonnage. Divisez pour obtenir la probabilité de l'événement.
\(P(E)=\dfrac{3}{6}=\dfrac{1}{2}\)
Un cube numérique est lancé. Détermine la probabilité de lancer un nombre supérieur à\(2\).
- Réponse
-
\(\dfrac{2}{3}\)
Calcul de la probabilité de l'union de deux événements
Nous cherchons souvent à déterminer la probabilité qu'un événement parmi plusieurs se produise. Supposons que nous jouions à un jeu de cartes et que nous gagnions si la prochaine carte tirée est un cœur ou un roi. Nous aimerions connaître la probabilité que la prochaine carte soit un cœur ou un roi. L'union de deux événements\(E\) et\(F\), écrit\(E\cup F\), est l'événement qui se produit si l'un ou les deux événements se produisent.
\[P(E\cup F)=P(E)+P(F)−P(E\cap F)\]
Supposons que le spinner de la figure\(\PageIndex{2}\) soit tourné. Nous voulons déterminer la probabilité de faire tourner une orange ou une\(b\).
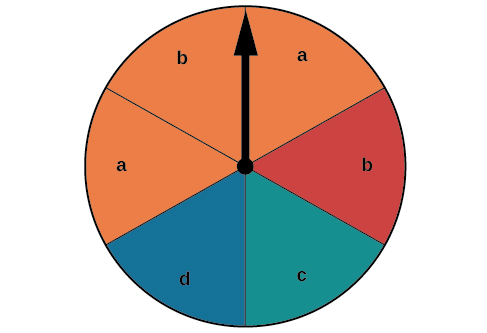
Figure\(\PageIndex{2}\) : Diagramme circulaire avec six options.
Il y a un total de\(6\) sections,\(3\) dont certaines sont oranges. Donc, la probabilité de faire tourner de l'orange est de\(\dfrac{3}{6}=\dfrac{1}{2}\). Il y a un total de\(6\) sections, et\(2\) parmi elles ont un\(b\). Donc, la probabilité de faire tourner un\(b\) est\(\dfrac{2}{6}=\dfrac{1}{3}\). Si nous additionnions ces deux probabilités, nous compterions le secteur qui est à la fois orange et un secteur\(b\) double. Pour déterminer la probabilité de faire tourner une orange ou un a\(b\), nous devons soustraire la probabilité que le secteur soit à la fois orange et possède un\(b\).
\(\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{6}=\dfrac{2}{3}\)
La probabilité de faire tourner une orange ou une\(b\) est\(\dfrac{2}{3}\).
La probabilité de l'union de deux événements\(E\) et\(F\) (écrite\(E\cup F\)) est égale à la somme de la probabilité\(E\) et de la probabilité de\(F\) moins la probabilité que\(E\) et\(F\) se produisent ensemble (ce que l'on appelle l'intersection de\(E\) \(F\)et s'écrit sous la forme\(E\cap F\)).
\[P(E\cup F)=P(E)+P(F)−P(E\cap F)\]
Une carte est tirée à partir d'un jeu de cartes standard. Déterminez la probabilité de dessiner un cœur ou un\(7\).
Solution
Un deck standard contient un nombre égal de cœurs, de diamants, de clubs et de piques. Donc, la probabilité de dessiner un cœur est\(\dfrac{1}{4}\). Il y en a quatre\(7s\) dans un deck standard, et il y a un total de\(52\) cartes. Donc, la probabilité de dessiner un\(7\) est\(\dfrac{1}{13}\).
La seule carte du jeu qui est à la fois un cœur et un a\(7\) est celle\(7\) des cœurs, donc la probabilité de tirer à la fois un cœur et un a\(7\) est\(\dfrac{1}{52}\). \(P(7)=\dfrac{1}{13}\)Substituez\(P(H)=\dfrac{1}{4}\), et\(P(H\cap 7)=\dfrac{1}{52}\) dans la formule.
\[\begin{align*} P(E\cup F) &=P(E)+P(F)−P(E\cap F) \\[4pt] &=\dfrac{1}{4}+\dfrac{1}{13}−\dfrac{1}{52} \\[4pt] &=\dfrac{4}{13} \end{align*}\]
La probabilité de dessiner un cœur ou un\(7\) est\(\dfrac{4}{13}\).
Une carte est tirée à partir d'un jeu de cartes standard. Déterminez la probabilité de tirer un carton rouge ou un as.
- Réponse
-
\(\dfrac{7}{13}\)
Calcul de la probabilité d'événements s'excluant mutuellement
Supposons que le spinner de Figure\(\PageIndex{2}\) soit à nouveau tourné, mais cette fois, nous nous intéressons à la probabilité de faire tourner une orange ou une\(d\). Aucun secteur n'est à la fois orange et ne contient un\(d\), donc ces deux événements n'ont aucun résultat en commun. Les événements sont considérés comme des événements qui s'excluent mutuellement lorsqu'ils n'ont aucun résultat en commun. Comme il n'y a pas de chevauchement, il n'y a rien à soustraire, donc la formule générale est
\[P(E\cap F)=P(E)+P(F)\]
Notez qu'avec les événements qui s'excluent mutuellement, l'intersection de\(E\) et\(F\) est l'ensemble vide. La probabilité de faire tourner une orange est\(\dfrac{3}{6}=\dfrac{1}{2}\) et la probabilité de faire tourner une orange\(d\) est\(\dfrac{1}{6}\). Nous pouvons déterminer la probabilité de faire tourner une orange ou une orange\(d\) simplement en additionnant les deux probabilités.
\[\begin{align*} P(E\cap F)&=P(E)+P(F) \\[4pt] &=\dfrac{1}{2}+\dfrac{1}{6} \\ &=\dfrac{2}{3} \end{align*}\]
La probabilité de faire tourner une orange ou une\(d\) est\(\dfrac{2}{3}\).
La probabilité de l'union de deux événements s'\(E\)excluant mutuellement\(F\) est donnée par
\[P(E\cap F)=P(E)+P(F)\]
- Déterminez le nombre total de résultats pour le premier événement.
- Déterminez la probabilité du premier événement.
- Déterminez le nombre total de résultats pour le deuxième événement.
- Déterminez la probabilité du deuxième événement.
- Ajoutez les probabilités.
Une carte est tirée à partir d'un jeu de cartes standard. Déterminez la probabilité de dessiner un cœur ou une bêche.
Solution
Les événements « dessiner un cœur » et « dessiner un chat » s'excluent mutuellement car ils ne peuvent pas se produire en même temps. La probabilité de dessiner un cœur est\(\dfrac{1}{4}\), et la probabilité de dessiner une bêche l'est également\(\dfrac{1}{4}\), de sorte que la probabilité de dessiner un cœur ou une bêche est
\(\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}\)
Une carte est tirée à partir d'un jeu de cartes standard. Déterminez la probabilité de dessiner un as ou un roi.
- Réponse
-
\(\dfrac{2}{13}\)
Utilisation de la règle du complément pour calculer les probabilités
Nous avons discuté de la façon de calculer la probabilité qu'un événement se produise. Parfois, nous cherchons à déterminer la probabilité qu'un événement ne se produise pas. Le complément d'un événement\(E\), désigné\(E′\), est l'ensemble des résultats de l'espace d'échantillonnage qui n'y figurent pas\(E\). Supposons, par exemple, que nous nous intéressions à la probabilité qu'un cheval perde une course. Si l'événement\(W\) est le cheval qui gagne la course, alors le complément de l'événement\(W\) est le cheval perdant la course.
Pour déterminer la probabilité que le cheval perde la course, nous devons utiliser le fait que la somme de toutes les probabilités d'un modèle de probabilité doit être\(1\).
\[P(E′)=1−P(E)\]
La probabilité que le cheval gagne ajoutée à la probabilité que le cheval perde doit être égale à\(1\). Par conséquent, si la probabilité que le cheval gagne la course est\(\dfrac{1}{9}\), la probabilité que le cheval perde la course est simplement
\(1−\dfrac{1}{9}=\dfrac{8}{9}\)
La probabilité que le complément d'un événement se produise est donnée par
\[P(E′)=1−P(E)\]
Deux cubes numériques à six faces sont roulés.
- Détermine la probabilité que la somme des nombres lancés soit inférieure ou égale à\(3\).
- Détermine la probabilité que la somme des nombres lancés soit supérieure à\(3\).
Solution
La première étape consiste à identifier l'espace d'échantillonnage, qui comprend tous les résultats possibles. Il existe deux cubes numériques, et chaque cube numérique a six résultats possibles. En utilisant le principe de multiplication, nous constatons qu'il existe\(6×6\) ou\(36\) que tous les résultats sont possibles. Ainsi, par exemple,\(1-1\) représente un\(1\) roulé sur chaque cube numérique.
| \(1-1\) | \(1-2\) | \(1-3\) | \(1-4\) | \(1-5\) | \(1-6\) |
| \(2-1\) | \(2-2\) | \(2-3\) | \(2-4\) | \(2-5\) | \(2-6\) |
| \(3-1\) | \(3-2\) | \(3-3\) | \(3-4\) | \(3-5\) | \(3-6\) |
| \(4-1\) | \(4-2\) | \(4-3\) | \(4-4\) | \(4-5\) | \(4-6\) |
| \(5-1\) | \(5-2\) | \(5-3\) | \(5-4\) | \(5-5\) | \(5-6\) |
| \(6-1\) | \(6-2\) | \(6-3\) | \(6-4\) | \(6-5\) | \(6-6\) |
- Nous devons compter le nombre de façons de générer une somme égale\(3\) ou inférieure. Cela inclurait les résultats suivants :\(1-1\)\(1-2\), et\(2-1\). Il n'y a donc que trois façons de générer une somme égale\(3\) ou inférieure. La probabilité est
\(\dfrac{3}{36}=\dfrac{1}{12}\)
- Plutôt que d'énumérer toutes les possibilités, nous pouvons utiliser la règle du complément. Comme nous avons déjà trouvé la probabilité du complément de cet événement, nous pouvons simplement soustraire cette probabilité\(1\) pour trouver la probabilité que la somme des nombres lancés soit supérieure à\(3\).
\[\begin{align*} P(E')&=1-P(E)\\ &=1-\dfrac{1}{12}\\ &=\dfrac{11}{12} \end{align*}\]
Deux cubes numériques sont roulés. Utilisez la règle du complément pour déterminer la probabilité que la somme soit inférieure à\(10\).
- Réponse
-
\(\dfrac{5}{6}\)
Calcul des probabilités en utilisant la théorie
De nombreux problèmes de probabilité intéressants concernent les principes de comptage, les permutations et les combinaisons. Dans ces problèmes, nous utiliserons des permutations et des combinaisons pour déterminer le nombre d'éléments dans les événements et les espaces d'échantillonnage. Ces problèmes peuvent être compliqués, mais ils peuvent être simplifiés en les subdivisant en problèmes de comptage plus petits.
Supposons, par exemple, qu'un magasin possède\(3\) des\(8\) téléphones portables et que ceux-ci sont défectueux. Nous voudrions peut-être déterminer la probabilité qu'un couple qui achète des\(2\) téléphones reçoivent des\(2\) téléphones qui ne sont pas défectueux. Pour résoudre ce problème, nous devons calculer toutes les méthodes de sélection des\(2\) téléphones qui ne sont pas défectueux ainsi que toutes les méthodes de sélection des\(2\) téléphones. Certains\(5\) téléphones ne sont pas défectueux, il existe donc des\(C(5,2)\) moyens de sélectionner des\(2\) téléphones qui ne sont pas défectueux. Il existe des\(8\) téléphones, donc il existe des\(C(8,2)\) moyens de sélectionner des\(2\) téléphones. La probabilité de sélectionner des\(2\) téléphones qui ne sont pas défectueux est la suivante :
\[ \begin{align*} \dfrac{\text{ways to select 2 phones that are not defective}}{\text{ways to select 2 phones}}&=\dfrac{C(5,2)}{C(8,2)} \\[4pt] &=\dfrac{10}{28} \\[4pt] &=\dfrac{5}{14} \end{align*}\]
Un enfant choisit au hasard\(5\) des jouets dans une poubelle contenant des\(3\) lapins, des\(5\) chiens et des\(6\) ours.
- Déterminez la probabilité que seuls les ours soient choisis.
- Déterminez la probabilité que\(2\) les ours et\(3\) les chiens soient choisis.
- Déterminez la probabilité qu'au moins\(2\) des chiens soient choisis.
Solution
- Nous devons compter le nombre de façons de ne choisir que les ours et le nombre total de façons possibles de sélectionner\(5\) des jouets. Il y a\(6\) des ours, il existe donc\(C(6,5)\) des moyens de\(5\) les choisir. Il y a\(14\) des jouets, donc il existe des\(C(14,5)\) moyens de choisir n'importe quel\(5\) jouet.
\(\dfrac{C(6,5)}{C(14,5)}=\dfrac{6}{2,002}=\dfrac{3}{1,001}\)
- Nous devons compter le nombre de façons de choisir les\(2\) ours et\(3\) les chiens et le nombre total de façons possibles de sélectionner les\(5\) jouets. Il y a\(6\) des ours, il existe donc\(C(6,2)\) des moyens de\(2\) les choisir. Il y a\(5\) des chiens, donc il existe\(C(5,3)\) des moyens de choisir\(3\) les chiens. Comme nous choisissons à la fois des ours et des chiens, nous utiliserons le principe de multiplication. Il existe des\(C(6,2)⋅C(5,3)\) moyens de choisir\(2\) les ours et\(3\) les chiens. Nous pouvons utiliser ce résultat pour déterminer la probabilité.
\(\dfrac{C(6,2)C(5,3)}{C(14,5)}=\dfrac{15⋅10}{2,002}=\dfrac{75}{1,001}\)
- Il est souvent plus facile de résoudre « au moins » les problèmes en utilisant la règle du complément. Nous commencerons par déterminer la probabilité que moins de\(2\) chiens soient choisis. Si moins de\(2\) chiens sont choisis, alors soit aucun chien ne peut être choisi, soit un\(1\) chien peut être choisi.
Quand aucun chien n'est choisi, tous les\(5\) jouets proviennent de\(9\) jouets qui ne sont pas des chiens. Il existe\(C(9,5)\) des moyens de choisir des jouets parmi les\(9\) jouets qui ne sont pas des chiens. Comme il existe\(14\) des jouets, il existe\(C(14,5)\) des moyens de choisir les\(5\) jouets parmi tous les jouets.
\(\dfrac{C(9,5)}{C(14,5)}=\dfrac{63}{1,001}\)
Si un\(1\) chien est choisi, les\(4\) jouets doivent provenir de\(9\) jouets qui ne sont pas des chiens et\(1\) doivent provenir des\(5\) chiens. Puisque nous choisissons à la fois des chiens et d'autres jouets, nous utiliserons le principe de multiplication. Il existe des\(C(5,1)⋅C(9,4)\) moyens de choisir\(1\) un chien et\(1\) d'autres jouets.
\(\dfrac{C(5,1)C(9,4)}{C(14,5)}=\dfrac{5⋅126}{2,002}=\dfrac{315}{1,001}\)
Comme ces événements ne se produiraient pas ensemble et s'excluent donc mutuellement, nous ajoutons les probabilités pour déterminer la probabilité que moins de\(2\) chiens soient choisis.
\(\dfrac{63}{1,001}+\dfrac{315}{1,001}=\dfrac{378}{1,001}\)
Nous soustrayons ensuite cette probabilité\(1\) pour déterminer la probabilité qu'au moins des\(2\) chiens soient choisis.
\(1−\dfrac{378}{1,001}=\dfrac{623}{1,001}\)
Un enfant choisit au hasard des\(3\) boules de gomme dans un contenant contenant des boules de gomme\(4\) violettes, des boules de gomme\(8\) jaunes et des boules de gomme\(2\) vertes.
- Détermine la probabilité que toutes les\(3\) boules de gomme sélectionnées soient violettes.
- Détermine la probabilité qu'aucune boule de gomme jaune ne soit sélectionnée.
- Détermine la probabilité qu'au moins une boule de gomme\(1\) jaune soit sélectionnée.
- Réponse
-
\(\dfrac{1}{91}\)
- Réponse
-
\(\dfrac{5}{91}\)
- Réponse
-
\(\dfrac{86}{91}\)
Accédez à ces ressources en ligne pour obtenir des instructions supplémentaires et vous entraîner avec probabilité.
Visitez ce site Web pour des questions pratiques supplémentaires sur Learningpod.
Équations clés
| probabilité d'un événement ayant des résultats tout aussi probables | \(P(E)=\dfrac{n(E)}{n(S)}\) |
| probabilité de l'union de deux événements | \(P(E\cup F)=P(E)+P(F)−P(E\cap F)\) |
| probabilité de l'union d'événements s'excluant mutuellement | \(P(E\cup F)=P(E)+P(F)\) |
| probabilité de la complémentarité d'un événement | \(P(E')=1−P(E)\) |
Key Concepts
- Probability is always a number between \(0\) and \(1\), where \(0\) means an event is impossible and \(1\) means an event is certain.
- The probabilities in a probability model must sum to \(1\). See Example \(\PageIndex{1}\).
- When the outcomes of an experiment are all equally likely, we can find the probability of an event by dividing the number of outcomes in the event by the total number of outcomes in the sample space for the experiment. See Example \(\PageIndex{2}\).
- To find the probability of the union of two events, we add the probabilities of the two events and subtract the probability that both events occur simultaneously. See Example \(\PageIndex{3}\).
- To find the probability of the union of two mutually exclusive events, we add the probabilities of each of the events. See Example \(\PageIndex{4}\).
- The probability of the complement of an event is the difference between \(1\) and the probability that the event occurs. See Example \(\PageIndex{5}\).
- In some probability problems, we need to use permutations and combinations to find the number of elements in events and sample spaces. See Example \(\PageIndex{6}\).


