13.6 : Théorème binomial
- Page ID
- 194882
- Appliquez le théorème binomial.
Un polynôme à deux termes est appelé binôme. Nous avons déjà appris à multiplier les binômes et à les élever à des puissances, mais élever un binôme à une puissance élevée peut être fastidieux et chronophage. Dans cette section, nous allons discuter d'un raccourci qui nous permettra de trouver\((x+y)^n\) sans multiplier le binôme par lui-même\(n\).
Identification des coefficients binomiaux
Dans le raccourci vers la recherche\({(x+y)}^n\), nous devrons utiliser des combinaisons pour trouver les coefficients qui apparaîtront dans l'expansion du binôme. Dans ce cas, nous utilisons la notation à la\(\dbinom{n}{r}\) place de\(C(n,r)\), mais elle peut être calculée de la même manière. Donc
\[\dbinom{n}{r}=C(n,r)=\dfrac{n!}{r!(n−r)!}\]
La combinaison\(\dbinom{n}{r}\) est appelée coefficient binomial. Voici un exemple de coefficient binomial :
\(\dbinom{5}{2}=C(5,2)=10\)
Si\(n\) et\(r\) sont des nombres entiers supérieurs ou égaux\(0\) à\(n≥r\), alors le coefficient binomial est
\[\dbinom{n}{r}=C(n,r)=\dfrac{n!}{r!(n−r)!} \label{binomial1}\]
Oui. Tout comme le nombre de combinaisons doit toujours être un nombre entier, un coefficient binomial sera toujours un nombre entier.
Détermine chaque coefficient binomial.
- \(\dbinom{5}{3}\)
- \(\dbinom{9}{2}\)
- \(\dbinom{9}{7}\)
Solution
Utilisez l'équation \ ref {binomial1} pour calculer chaque coefficient binomial. Vous pouvez également utiliser la\(nC_r\) fonction de votre calculatrice.
- \(\dbinom{5}{3}=\dfrac{5!}{3!(5−3)!}=\dfrac{5⋅4⋅3!}{3!2!}=10\)
- \(\dbinom{9}{2}=\dfrac{9!}{2!(9−2)!}=\dfrac{9⋅8⋅7!}{2!7!}=36\)
- \(\dbinom{9}{7}=\dfrac{9!}{7!(9−7)!}=\dfrac{9⋅8⋅7!}{7!2!}=36\)
Analyse
Notez que nous avons obtenu le même résultat pour les parties (b) et (c). Si vous examinez attentivement la solution pour ces deux parties, vous constaterez que vous vous retrouvez avec les deux mêmes facteurs dans le dénominateur, mais que l'ordre est inversé, tout comme pour les combinaisons.
\[\dbinom{n}{r}=\dbinom{n}{n−r} \nonumber\]
Détermine chaque coefficient binomial.
- \(\dbinom{7}{3}\)
- \(\dbinom{11}{4}\)
- Répondez à une
-
\(35\)
- Réponse b
-
\(33\)
Utilisation du théorème binomial
Lorsque nous développons\({(x+y)}^n\) en multipliant, le résultat est appelé expansion binomiale et inclut des coefficients binomiaux. Si nous voulions nous développer\({(x+y)}^{52}\), nous pourrions nous multiplier\((x+y)\) par nous-mêmes cinquante-deux fois. Cela peut prendre des heures ! Si nous examinons quelques extensions binomiales simples, nous pouvons trouver des modèles qui nous mèneront à un raccourci pour trouver des extensions binomiales plus complexes.
\[\begin{align*} {(x+y)}^2 &= x^2+2xy+y^2 \\[4pt] {(x+y)}^3 &= x^3+3x^2y+3xy^2+y^3 \\[4pt] {(x+y)}^4 &= x^4+4x^3y+6x^2y^2+4xy^3+y^4 \end{align*}\]
Examinons d'abord les exposants. À chaque terme successif, l'exposant pour les\(x\) diminutions et l'exposant pour les\(y\) augmentations. La somme des deux exposants est\(n\) pour chaque terme.
Examinons ensuite les coefficients. Notez que les coefficients augmentent puis diminuent selon un schéma symétrique. Les coefficients suivent un schéma :
\(\dbinom{n}{0}\),\(\dbinom{n}{1}\),\(\dbinom{n}{2}\),...,\(\dbinom{n}{n}.\)
Ces modèles nous mènent au théorème binomial, qui peut être utilisé pour étendre n'importe quel binôme.
\[\begin{align*} {(x+y)}^n&=\sum_{k=0}^{n}\dbinom{n}{k}x^{n−k}y^k \\[4pt] &=x^n+\dbinom{n}{1}x^{n−1}y+\dbinom{n}{2}x^{n−2}y^2+...+\dbinom{n}{n−1}xy^{n−1}+y^n \end{align*}\]
Une autre façon de voir les coefficients est d'examiner l'expansion d'un binôme sous forme générale,\(x+y\), à des puissances successives\(1\)\(2\),\(3\), et\(4\).
\[\begin{align*} {(x+y)}^1 &= x+y \\ {(x+y)}^2 &= x^2+2xy+y^2 \\ {(x+y)}^3 &= x^3+3x^2y+3xy^2+y^3 \\ {(x+y)}^4 &= x^4+4x^3y+6x^2y^2+4xy^3+y^4 \end{align*}\]
Pouvez-vous deviner la prochaine extension du binôme\({(x+y)}^5\) ?

Figurine\(\PageIndex{1}\)
Voir la figure\(\PageIndex{1}\), qui illustre ce qui suit :
- Il existe des\(n+1\) termes dans l'expansion de\({(x+y)}^n\).
- Le degré (ou la somme des exposants) pour chaque terme est\(n\).
- Les pouvoirs\(x\) commencent par\(n\) et diminuent jusqu'à\(0\).
- Les pouvoirs\(y\) commencent par\(0\) et augmentent jusqu'à\(n\).
- Les coefficients sont symétriques.
Pour déterminer l'expansion\({(x+y)}^5\), nous voyons\(n=5\) donc qu'il y aura des\(5+1=6\) termes. Chaque terme a un degré combiné de\(5\). Par ordre décroissant pour les puissances de\(x\), le schéma est le suivant :
- Introduisez\(x^5\), puis pour chaque terme successif, réduisez l'\(x\)exposant\(1\) jusqu'à ce qu'\(x^0=1\)il soit atteint.
- Introduisez\(y^0=1\), puis augmentez l'exposant sur yy de 1 jusqu'à ce qu'\(y^5\)il soit atteint.
\(x^5, x^4y, x^3y^2, x^2y^3, xy^4, y^5\)
La prochaine extension serait
\({(x+y)}^5=x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5\)
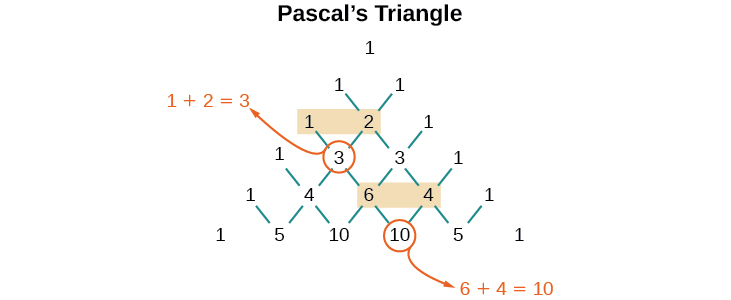
Mais d'où viennent ces coefficients ? Les coefficients binomiaux sont symétriques. Nous pouvons voir ces coefficients dans un tableau connu sous le nom de triangle de Pascal, illustré sur la figure\(\PageIndex{2}\).
Figurine\(\PageIndex{2}\)
Pour générer le triangle de Pascal, nous commençons par écrire un\(1\). Dans la ligne ci-dessous, ligne 2, nous en écrivons deux\(1’s\). Dans la troisième rangée, flanquez les extrémités des rangées avec\(1’s\), et ajoutez\(1+1\) pour trouver le chiffre du milieu,\(2\). Dans la\(n^{th}\) rangée, flanquez les extrémités de la rangée avec\(1’s\). Chaque élément du triangle est la somme des deux éléments situés juste au-dessus.
Pour voir le lien entre le triangle de Pascal et les coefficients binomiaux, revenons sur l'expansion des binômes sous leur forme générale.
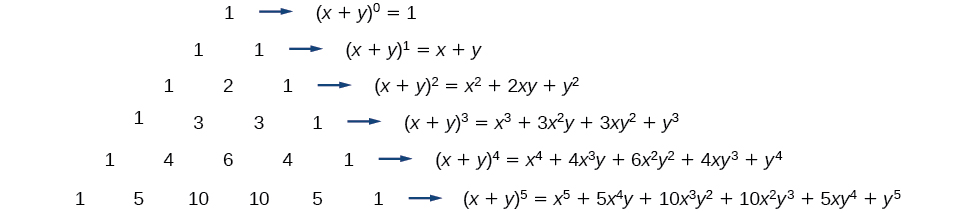
Le théorème binomial est une formule qui peut être utilisée pour développer n'importe quel binôme.
\[ {(x+y)}^n = \sum_{k=0}^{n}\dbinom{n}{k}x^{n−k}y^k = x^n+\dbinom{n}{1}x^{n−1}y+\dbinom{n}{2}x^{n−2}y^2+...+\dbinom{n}{n−1}xy^{n−1}+y^n \]
- Déterminez la valeur de en\(n\) fonction de l'exposant.
- Évaluez le\(k=0\) via à\(k=n\) l'aide de la formule du théorème binomial.
- Simplifiez.
Écrivez sous une forme développée.
- \({(x+y)}^5\)
- \({(3x−y)}^4\)
Solution
a. Substituer\(n=5\) dans la formule. Évaluez les\(k=0\)\(k=5\) termes principaux. Simplifiez.
\[\begin{align*} {(x+y)}^5 &= \dbinom{5}{0}x^5y^0+\dbinom{5}{1}x^4y^1+\dbinom{5}{2}x^3y^2+\dbinom{5}{3}x^2y^3+\dbinom{5}{4}x^1y^4+\dbinom{5}{5}x^0y^5 \\ {(x+y)}^5 &= x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5 \end{align*}\]
b. Substituer\(n=4\) dans la formule. Évaluez les\(k=0\)\(k=4\) termes principaux. Remarquez qu'\(3x\)il se trouve à l'endroit qui était occupé par\(x\) et qui\(–y\) se trouve à l'endroit qui était occupé par\(y\). Nous les remplaçons donc. Simplifiez.
\[\begin{align*} {(3x−y)}^4 &= \dbinom{4}{0}{(3x)}^4{(−y)}^0+\dbinom{4}{1}{(3x)}^3{(−y)}^1+\dbinom{4}{2}{(3x)}^2{(−y)}^2+\dbinom{4}{3}{(3x)}^1{(−y)}^3+\dbinom{4}{4}{(3x)}^0{(−y)}^4 \\ {(3x−y)}^4 &= 81x^4−108x^3y+54x^2y^2−12xy^3+y^4 \end{align*}\]
Analyse
Remarquez les signes alternés dans la partie b. Cela se produit parce que le\((−y)\) fait d'être élevé à des puissances impaires est négatif, mais\((−y)\) élevé à des puissances paires est positif. Cela se produit chaque fois que le binôme contient un signe de soustraction.
Écrivez sous une forme développée.
- \({(x−y)}^5\)
- \({(2x+5y)}^3\)
- Répondez à une
-
\(x^5−5x^4y+10x^3y^2−10x^2y^3+5xy^4−y^5\)
- Réponse b
-
\(8x^3+60x^2y+150xy^2+125y^3\)
Utiliser le théorème binomial pour trouver un seul terme
L'extension d'un binôme avec un exposant élevé, par exemple,\({(x+2y)}^{16}\) peut être un processus long. Parfois, nous ne nous intéressons qu'à un certain terme d'une expansion binomiale. Il n'est pas nécessaire de développer complètement un binôme pour trouver un seul terme spécifique.
Notez le schéma des coefficients dans l'expansion de\({(x+y)}^5\).
\({(x+y)}^5=x^5+\dbinom{5}{1}x^4y+\dbinom{5}{2}x^3y^2+\dbinom{5}{3}x^2y^3+\dbinom{5}{4}xy^4+y^5\)
Le deuxième terme est\(\dbinom{5}{1}x^4y\). Le troisième terme est\(\dbinom{5}{2}x^3y^2\). Nous pouvons généraliser ce résultat.
Le\((r+1)\) 6ème terme de l'expansion binomiale de\({(x+y)}^n\) est :
\[\dbinom{n}{r}x^{n−r}y^r \label{binomial5}\]
- Déterminez la valeur de nn en fonction de l'exposant.
- Déterminez\((r+1)\).
- Déterminez\(r\).
- Remplacer\(r\) dans la formule\((r+1)\) le terme de l'expansion binomiale.
Trouve le dixième terme de\({(x+2y)}^{16}\) sans développer complètement le binôme.
Solution
Comme nous recherchons le dixième terme\(r+1=10\), nous utiliserons\(r=9\) dans nos calculs l'équation \ ref {binomial5}.
\(\dbinom{16}{9}x^{16−9}{(2y)}^9=5,857,280x^7y^9\)
Trouve le sixième terme de\({(3x−y)}^9\) sans développer complètement le binôme.
- Réponse
-
\(−10,206x^4y^5\)
Accédez à ces ressources en ligne pour obtenir des instructions et des exercices supplémentaires grâce à l'expansion binomiale.
Équations clés
| Théorème binomial | \({(x+y)}^n=\sum_{k=0}^n\dbinom{n}{k}x^{n−k}y^k\) |
| \((r+1)\)le terme d'une expansion binomiale | \(\dbinom{n}{r}x^{n−r}y^r\) |
Key Concepts
- \(\dbinom{n}{r}\) is called a binomial coefficient and is equal to \(C(n,r)\). See Example \(\PageIndex{1}\).
- The Binomial Theorem allows us to expand binomials without multiplying. See Example \(\PageIndex{2}\).
- We can find a given term of a binomial expansion without fully expanding the binomial. See Example \(\PageIndex{3}\).


